 明治大学
明治大学
 明治大学
明治大学
福田の数学〜明治大学2024理工学部第3問〜放物線と折れ線の位置関係
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
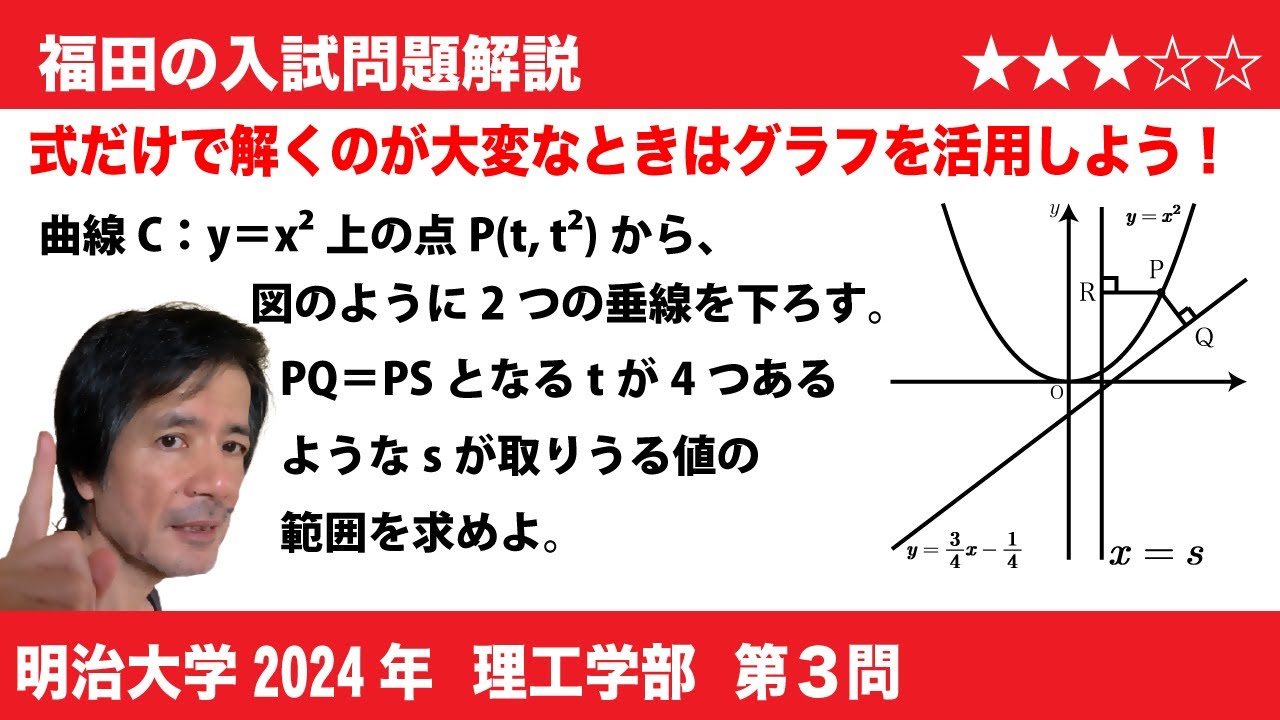
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
この動画を見る
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
#明治大学2023#極限_48

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
この動画を見る
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
福田の数学〜明治大学2024理工学部第2問〜三角関数の増減と面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
この動画を見る
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
福田の数学〜明治大学2024理工学部第1問(4)〜部屋分けの方法

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$5$ 人の中学生 $\mathrm{A,B,C,D,E}$ と $3$ 人の高校生 $\mathrm{F,G,H}$ の合計 $8$ 人の生徒が、 $2$ つの部屋 $\mathrm{X,Y}$ に分かれて入る。ただし、どの生徒も必ずどちらかの部屋に入るものとする。
(a) どちらの部屋にも $1$ 人以上の生徒が入るような入り方は $\fbox{トナニ}$ 通りである。
(b) どちらの部屋にも $1$ 人以上の中学生が入るような入り方は $\fbox{ヌネノ}$ 通りである。
(c) どちらの部屋にも $1$ 人以上の中学生と $1$ 人以上の高校生が入るような入り方は $\fbox{ハヒフ}$ 通りである。
(d) どちらの部屋も中学生の人数が高校生の人数より多くなるような入り方は $\fbox{ヘホ}$ 通りである。ただし、どちらの部屋にも $1$ 人以上の高校生が入るものとする。
この動画を見る
$5$ 人の中学生 $\mathrm{A,B,C,D,E}$ と $3$ 人の高校生 $\mathrm{F,G,H}$ の合計 $8$ 人の生徒が、 $2$ つの部屋 $\mathrm{X,Y}$ に分かれて入る。ただし、どの生徒も必ずどちらかの部屋に入るものとする。
(a) どちらの部屋にも $1$ 人以上の生徒が入るような入り方は $\fbox{トナニ}$ 通りである。
(b) どちらの部屋にも $1$ 人以上の中学生が入るような入り方は $\fbox{ヌネノ}$ 通りである。
(c) どちらの部屋にも $1$ 人以上の中学生と $1$ 人以上の高校生が入るような入り方は $\fbox{ハヒフ}$ 通りである。
(d) どちらの部屋も中学生の人数が高校生の人数より多くなるような入り方は $\fbox{ヘホ}$ 通りである。ただし、どちらの部屋にも $1$ 人以上の高校生が入るものとする。
福田の数学〜明治大学2024理工学部第1問(3)〜x軸まわりとy軸まわりの回転体の体積
単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
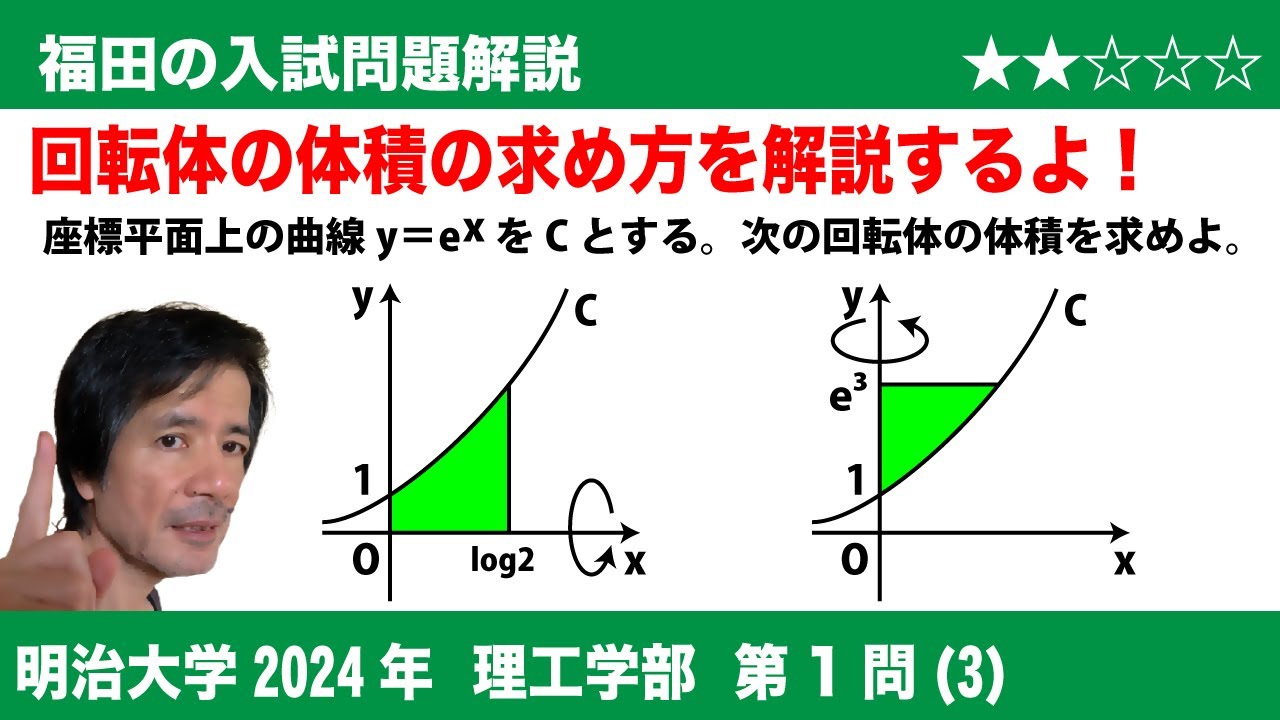
座標平面上の曲線 $y=e^x$ を $C$ とする。
(a) 曲線 $C$ と $x$ 軸および $2$ 直線 $x=0,x=\log 2$ で囲まれた部分を、 $x$ 軸のまわりに $1$ 回転してできる立体の体積は $\displaystyle \frac{\fbox{タ}}{\fbox{チ}}\pi$ である。
(b) 曲線 $C$ と $y$ 軸および直線 $y=e^3$ で囲まれた部分を、 $y$ 軸のまわりに $1$ 回転してできる立体の体積は $(\fbox{ツ}e^3-\fbox{テ})\pi$ である。
ただし、 $\log x$ は $x$ の自然対数を表し、 $e$ は自然対数の底である。
この動画を見る
座標平面上の曲線 $y=e^x$ を $C$ とする。
(a) 曲線 $C$ と $x$ 軸および $2$ 直線 $x=0,x=\log 2$ で囲まれた部分を、 $x$ 軸のまわりに $1$ 回転してできる立体の体積は $\displaystyle \frac{\fbox{タ}}{\fbox{チ}}\pi$ である。
(b) 曲線 $C$ と $y$ 軸および直線 $y=e^3$ で囲まれた部分を、 $y$ 軸のまわりに $1$ 回転してできる立体の体積は $(\fbox{ツ}e^3-\fbox{テ})\pi$ である。
ただし、 $\log x$ は $x$ の自然対数を表し、 $e$ は自然対数の底である。
福田の数学〜明治大学2024理工学部第1問(2)〜空間ベクトルと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$k$ を正の実数とし、座標空間内の $4$ 点 $\mathrm{O}(0,0,0),$ $\mathrm{A}(k,2,1),$ $\mathrm{B}(-k,1,2),$ $\mathrm{C}(1,1,1)$ を考える。 $2$ つのベクトル $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ は垂直であるとする。また、 $3$ 点 $\mathrm{O},\mathrm{A},\mathrm{B}$ を通る平面を $\alpha$ とし、点 $\mathrm{C}$ から$\alpha$ へ下ろした垂線と平面 $\alpha$ の交点を $\mathrm{H}$ とする。このとき、 $k=\fbox{キ}$ であり、 $\triangle \mathrm{OAB}$ の面積は $\displaystyle \frac{\fbox{ク}}{\fbox{ケ}}$ である。また、$\overrightarrow{\mathrm{OH}}=$$\displaystyle \frac{\fbox{コ}}{\fbox{サ}} \overrightarrow{\mathrm{OA}}$$\displaystyle + \frac{\fbox{シ}}{\fbox{ス}} \overrightarrow{\mathrm{OB}}$ であり、四面体 $\mathrm{OABC}$ の体積は $\displaystyle \frac{\fbox{セ}}{\fbox{ソ}}$ である。
この動画を見る
$k$ を正の実数とし、座標空間内の $4$ 点 $\mathrm{O}(0,0,0),$ $\mathrm{A}(k,2,1),$ $\mathrm{B}(-k,1,2),$ $\mathrm{C}(1,1,1)$ を考える。 $2$ つのベクトル $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ は垂直であるとする。また、 $3$ 点 $\mathrm{O},\mathrm{A},\mathrm{B}$ を通る平面を $\alpha$ とし、点 $\mathrm{C}$ から$\alpha$ へ下ろした垂線と平面 $\alpha$ の交点を $\mathrm{H}$ とする。このとき、 $k=\fbox{キ}$ であり、 $\triangle \mathrm{OAB}$ の面積は $\displaystyle \frac{\fbox{ク}}{\fbox{ケ}}$ である。また、$\overrightarrow{\mathrm{OH}}=$$\displaystyle \frac{\fbox{コ}}{\fbox{サ}} \overrightarrow{\mathrm{OA}}$$\displaystyle + \frac{\fbox{シ}}{\fbox{ス}} \overrightarrow{\mathrm{OB}}$ であり、四面体 $\mathrm{OABC}$ の体積は $\displaystyle \frac{\fbox{セ}}{\fbox{ソ}}$ である。
福田の数学〜明治大学2024理工学部第1問(1)〜高次方程式と整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
この動画を見る
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
福田の数学〜明治大学2024全学部統一III第3問〜外サイクロイド曲線と曲線の長さ

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3} a\gt 0$とする。座標平面で、原点$O$を中心とする半径$a$の定円を$C_1$とし、$C_1$と外接する半径$a$の円を$C_2$とする。円$C_2$が定円$C_1$と外接しながらすべることなく転がるとき、$C_2$上の定点$P$が描く曲線を考えたい。始めに$C_2$の中心が$(2a,0)$にあり、$P$が$(a,0)$にあるとする。$C_2$の中心が点$(2a,0)$から原点$O$を中心に反時計回りに$θ$だけ回転した位置にきたとき、$C_1$と$C_2$の接点を通る$C_1$と$C_2$の共通の接線を$l_θ$とする。$l_θ$の方程式は$a=(\boxed{ア})x+(\boxed{イ})y$である。このとき、$P$は直線$l_θ$に関して$(a,0)$と対称な点であるので、$P$の座標を$(x,y)$とすると、$P$の軌跡は$θ$を媒介変数として$x=2a(\boxed{ウ})cosθ+a, y=2a(\boxed{ウ})sinθ$と表される。
$x$と$y$をそれぞれ$θ$で微分すると$\frac{dx}{dθ}=2a(\boxed{エ}),\frac{dy}{dθ}=2a(\boxed{オ})$となるので、$θ$が0から2まで動くとき、$P$が描く曲線の長さは$\boxed{カキ}a$である。
この動画を見る
$\boxed{3} a\gt 0$とする。座標平面で、原点$O$を中心とする半径$a$の定円を$C_1$とし、$C_1$と外接する半径$a$の円を$C_2$とする。円$C_2$が定円$C_1$と外接しながらすべることなく転がるとき、$C_2$上の定点$P$が描く曲線を考えたい。始めに$C_2$の中心が$(2a,0)$にあり、$P$が$(a,0)$にあるとする。$C_2$の中心が点$(2a,0)$から原点$O$を中心に反時計回りに$θ$だけ回転した位置にきたとき、$C_1$と$C_2$の接点を通る$C_1$と$C_2$の共通の接線を$l_θ$とする。$l_θ$の方程式は$a=(\boxed{ア})x+(\boxed{イ})y$である。このとき、$P$は直線$l_θ$に関して$(a,0)$と対称な点であるので、$P$の座標を$(x,y)$とすると、$P$の軌跡は$θ$を媒介変数として$x=2a(\boxed{ウ})cosθ+a, y=2a(\boxed{ウ})sinθ$と表される。
$x$と$y$をそれぞれ$θ$で微分すると$\frac{dx}{dθ}=2a(\boxed{エ}),\frac{dy}{dθ}=2a(\boxed{オ})$となるので、$θ$が0から2まで動くとき、$P$が描く曲線の長さは$\boxed{カキ}a$である。
福田の数学〜明治大学2024全学部統一III第2問〜複素数平面上の点の移動と確率

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
この動画を見る
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
福田の数学〜明治大学2024全学部統一III第1問(2)〜定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
この動画を見る
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
福田の数学〜明治大学2024全学部統一IⅡAB第3問〜変わった規則の数列と点列と面積

単元:
#大学入試過去問(数学)#平面上のベクトル#複素数平面#数列#平面上のベクトルと内積#漸化式#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle
\fcolorbox{#000}{ #fff }{3}
整数からなる数列\{a_n\} \ (n=1,2,3,...)を次の規則1、2により定める。
$
$\displaystyle
(規則1)a_1=0 , \ a_2=1である。
$
$
\displaystyle(規則2)k=1,2,3,...について、初項から第2^{k+1}項までに値のそれぞれに1を加え、\\ それらすべてを逆の順序にしたものが第2^k+1項から第2^{k+1}項までの値と定める。
$
$\displaystyle
(1)以上の規則により得られる数列\{ a_n \}において、a_{10}=\fcolorbox{#000}{ #fff }{$ア \ \ \ $}であり、a_{16}=\fcolorbox{#000}{ #fff }{$イ \ \ \ $}である。 \\
また第2^k項(k=5,6,7,...)の値は\fcolorbox{#000}{ #fff }{$ウ \ \ \ $}である。
$
$\displaystyle
(2)a_{518}を求めたい。上記の規則2によれば、1 \leqq i \leqq 2^kを満たすiに対して、 \\
a_iに1を加えた数と第
\fcolorbox{#000}{ #fff }{$エ \ \ \ $}
項が、等しいと定めている。 \\
実際に、2^b < 518 \leqq 2^{b+1}を満たすような整数bは
\fcolorbox{#000}{ #fff }{$オ \ \ \ $}
であることに注意すれば、a_{518}=
\fcolorbox{#000}{ #fff }{$カ \ \ \ $}
である。
$
$\displaystyle
(3)点O_k(k=1,2,3,...)を次のように定める。\\
数列 \{ a_n \}の初項から第2^k項に着目し、a_nを4で割った余りにしたがって、ベクトル\vec{e_n}を
$
$
\vec{e_n}=
\left\{
\begin{array}{l}
(1,0) \quad a_nが4の倍数のとき \\
(0,1) \quad a_nを4で割った余りが1のとき \\
(-1,0) \quad a_nが4で割った余りが2のとき \\
(0,-1) \quad a_nを4で割った余りが3のとき
\end{array}
\right.
$
$
\displaystyle
によって定め、\\
点P_1の位置ベクトルを\overrightarrow{OP_1}=\vec{e_1}+\vec{e_2}とし、\\
点P_k(k=2,3,4,...)の位置ベクトルを\\
\overrightarrow{OP_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+...+\vec{e_{2^k}}とする。\\
たとえば、 \\
\overrightarrow{OP_w}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)である。\\
\{a_n\}を定める規則に注目すると、 \\
\overrightarrow{OP_{k+1}} は \overrightarrow{OP_k} の\fcolorbox{#000}{ #fff }{$キ \ \ \ $}倍であり、\\
\angle P_kOP_{k+1}=\fcolorbox{#000}{ #fff }{$ク \ \ \ $}である。\\
このことから\\
\overrightarrow{OP_{99}}=(\fcolorbox{#000}{ #fff }{$ケ \ \ \ $},\fcolorbox{#000}{ #fff }{$コ \ \ \ $})である。
$
この動画を見る
$\displaystyle
\fcolorbox{#000}{ #fff }{3}
整数からなる数列\{a_n\} \ (n=1,2,3,...)を次の規則1、2により定める。
$
$\displaystyle
(規則1)a_1=0 , \ a_2=1である。
$
$
\displaystyle(規則2)k=1,2,3,...について、初項から第2^{k+1}項までに値のそれぞれに1を加え、\\ それらすべてを逆の順序にしたものが第2^k+1項から第2^{k+1}項までの値と定める。
$
$\displaystyle
(1)以上の規則により得られる数列\{ a_n \}において、a_{10}=\fcolorbox{#000}{ #fff }{$ア \ \ \ $}であり、a_{16}=\fcolorbox{#000}{ #fff }{$イ \ \ \ $}である。 \\
また第2^k項(k=5,6,7,...)の値は\fcolorbox{#000}{ #fff }{$ウ \ \ \ $}である。
$
$\displaystyle
(2)a_{518}を求めたい。上記の規則2によれば、1 \leqq i \leqq 2^kを満たすiに対して、 \\
a_iに1を加えた数と第
\fcolorbox{#000}{ #fff }{$エ \ \ \ $}
項が、等しいと定めている。 \\
実際に、2^b < 518 \leqq 2^{b+1}を満たすような整数bは
\fcolorbox{#000}{ #fff }{$オ \ \ \ $}
であることに注意すれば、a_{518}=
\fcolorbox{#000}{ #fff }{$カ \ \ \ $}
である。
$
$\displaystyle
(3)点O_k(k=1,2,3,...)を次のように定める。\\
数列 \{ a_n \}の初項から第2^k項に着目し、a_nを4で割った余りにしたがって、ベクトル\vec{e_n}を
$
$
\vec{e_n}=
\left\{
\begin{array}{l}
(1,0) \quad a_nが4の倍数のとき \\
(0,1) \quad a_nを4で割った余りが1のとき \\
(-1,0) \quad a_nが4で割った余りが2のとき \\
(0,-1) \quad a_nを4で割った余りが3のとき
\end{array}
\right.
$
$
\displaystyle
によって定め、\\
点P_1の位置ベクトルを\overrightarrow{OP_1}=\vec{e_1}+\vec{e_2}とし、\\
点P_k(k=2,3,4,...)の位置ベクトルを\\
\overrightarrow{OP_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+...+\vec{e_{2^k}}とする。\\
たとえば、 \\
\overrightarrow{OP_w}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)である。\\
\{a_n\}を定める規則に注目すると、 \\
\overrightarrow{OP_{k+1}} は \overrightarrow{OP_k} の\fcolorbox{#000}{ #fff }{$キ \ \ \ $}倍であり、\\
\angle P_kOP_{k+1}=\fcolorbox{#000}{ #fff }{$ク \ \ \ $}である。\\
このことから\\
\overrightarrow{OP_{99}}=(\fcolorbox{#000}{ #fff }{$ケ \ \ \ $},\fcolorbox{#000}{ #fff }{$コ \ \ \ $})である。
$
福田の数学〜明治大学2024全学部統一IⅡAB第2問〜高次方程式の解と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$についての関数$f(x), g(x), h(x)$を$f(x) = 4x^4, g(x) = 12x + 8, h(x) = 4x^2+1$により定める。座標平面上で曲線 $y = f(x)$と直線$y=g(x)$は、異なる2点で交わる。それら交点の$x$座標を$a, b$ ($a \lt b$)とする。
(1) $f(x)+h(x) = (\fbox{ ア }x^2+\fbox{ イ })^2, g(x)+h(x) = (\fbox{ ウ }x+\fbox{ エ })^2$である。
(2) $a+b=\fbox{ オ }, b-a=\sqrt{ \fbox{ カ } }$である。
この動画を見る
$x$についての関数$f(x), g(x), h(x)$を$f(x) = 4x^4, g(x) = 12x + 8, h(x) = 4x^2+1$により定める。座標平面上で曲線 $y = f(x)$と直線$y=g(x)$は、異なる2点で交わる。それら交点の$x$座標を$a, b$ ($a \lt b$)とする。
(1) $f(x)+h(x) = (\fbox{ ア }x^2+\fbox{ イ })^2, g(x)+h(x) = (\fbox{ ウ }x+\fbox{ エ })^2$である。
(2) $a+b=\fbox{ オ }, b-a=\sqrt{ \fbox{ カ } }$である。
#明治大学2023#定積分_24#元高校教員
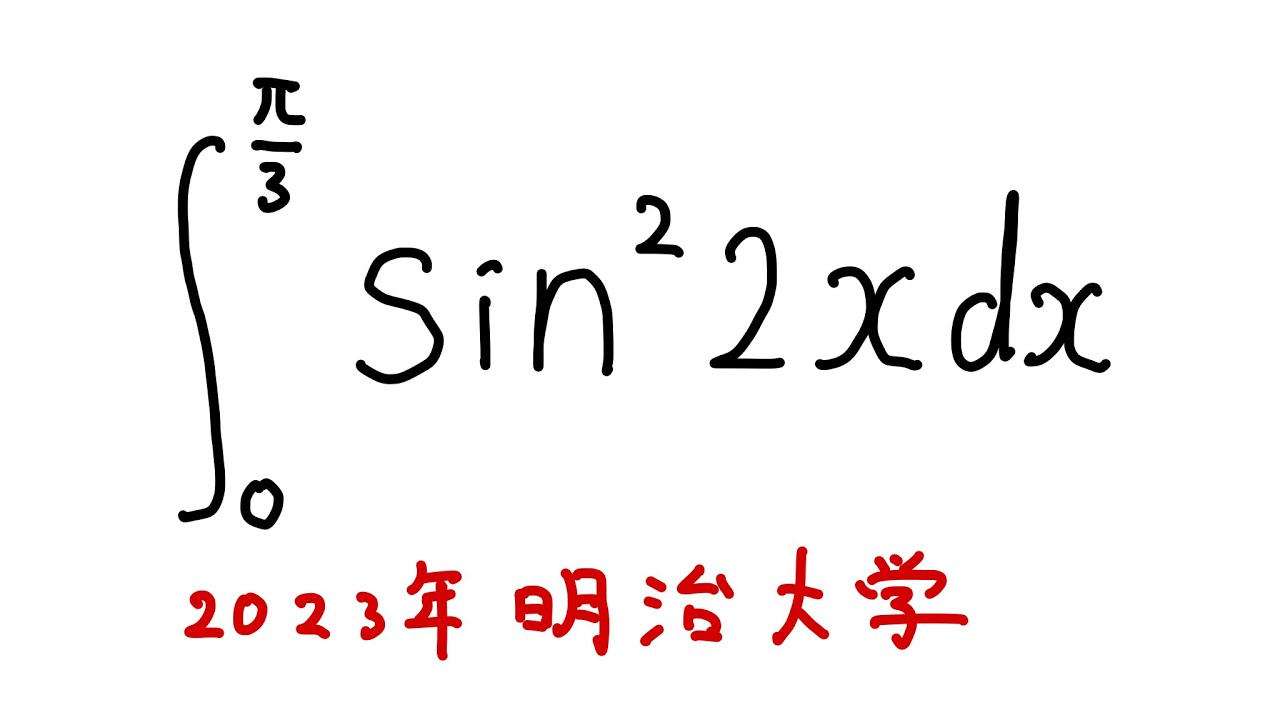
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}} \sin^2 2x dx$
出典:2023年明治大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}} \sin^2 2x dx$
出典:2023年明治大学
福田の数学〜明治大学2024全学部統一IⅡAB第1問(2)〜対数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$についての不等式$\left( \log_{ 3 } \frac{x}{8}\right)\cdot\left( \log_{ 2 }8x\right)\leqq \left( \log_{ 3 }2\right)\cdot\left( \log_{ 2 } \frac{8}{x}\right)$を解くと、$\frac{\fbox{ ク }}{\fbox{ ケコ }}\leqq x \leqq \fbox{ サ }$である。
この動画を見る
$x$についての不等式$\left( \log_{ 3 } \frac{x}{8}\right)\cdot\left( \log_{ 2 }8x\right)\leqq \left( \log_{ 3 }2\right)\cdot\left( \log_{ 2 } \frac{8}{x}\right)$を解くと、$\frac{\fbox{ ク }}{\fbox{ ケコ }}\leqq x \leqq \fbox{ サ }$である。
福田の数学〜明治大学2024全学部統一IⅡAB第1問(1)〜接線と法線の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
この動画を見る
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
#明治大学 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{3x}}{e^x+1} dx$
出典:明治大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{3x}}{e^x+1} dx$
出典:明治大学
大学入試問題#801「1番は、みるからに1だけど」 #明治大学(2011) #極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1.$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{log(n+5)}{log(n+2)}$
2.数列$\{a_n\},\{b_n\}$をそれぞれ$a_n=(n+5)^{-2n+1},b_n=\displaystyle \frac{1}{n\ log(n+2)}$で定める。
このとき、$\displaystyle \lim_{ n \to \infty } (a_n)^b_n$を求めよ。
出典:2011年明治大学 入試問題
この動画を見る
1.$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{log(n+5)}{log(n+2)}$
2.数列$\{a_n\},\{b_n\}$をそれぞれ$a_n=(n+5)^{-2n+1},b_n=\displaystyle \frac{1}{n\ log(n+2)}$で定める。
このとき、$\displaystyle \lim_{ n \to \infty } (a_n)^b_n$を求めよ。
出典:2011年明治大学 入試問題
福田の数学〜よくある図形問題ですが微分で困ったことに〜明治大学2023年理工学部第3問〜三角比と最大
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
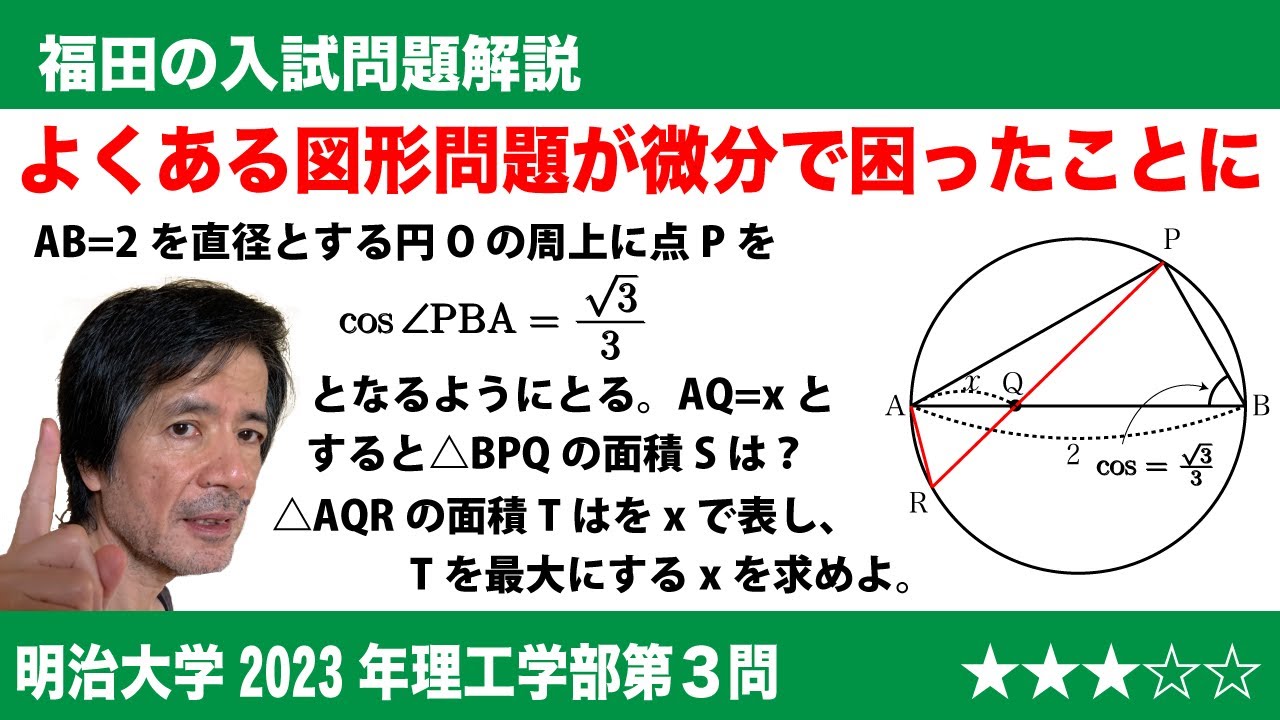
[ 3 ]長さ 2 の線分 AB を直径とする円 O の周上に、点 P を$cos\angle PBA=\dfrac{\sqrt{3}}{3}$となるようにとる。このとき、 BP =$\fbox{か}$である。線分 AB 上に A, B とは異なる点 Q をとり、$x= AQ ( 0 くxく 2 )$とする。 PQ をxの式で表すと PQ =$\fbox{き}$となる。また、三角形 BPQ の面積 s をxの式で表すと s =$\fbox{く}$である。直線 PQ と円 O の交点のうち、 P でないものを R とする。三角形 AQR の面積Tをxの式で表すとT=$\fbox{け}$である。また、$0 くxく2$の範囲でxを動かすとき、Tが最大になるのは$x=\fbox{こ}$のときだけである。
2023明治大学理工学部過去問
この動画を見る
[ 3 ]長さ 2 の線分 AB を直径とする円 O の周上に、点 P を$cos\angle PBA=\dfrac{\sqrt{3}}{3}$となるようにとる。このとき、 BP =$\fbox{か}$である。線分 AB 上に A, B とは異なる点 Q をとり、$x= AQ ( 0 くxく 2 )$とする。 PQ をxの式で表すと PQ =$\fbox{き}$となる。また、三角形 BPQ の面積 s をxの式で表すと s =$\fbox{く}$である。直線 PQ と円 O の交点のうち、 P でないものを R とする。三角形 AQR の面積Tをxの式で表すとT=$\fbox{け}$である。また、$0 くxく2$の範囲でxを動かすとき、Tが最大になるのは$x=\fbox{こ}$のときだけである。
2023明治大学理工学部過去問
福田の数学〜曲線の長さの計算は大丈夫?〜明治大学2023年理工学部第2問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\dfrac{1}{8}x^2-logx(x \gt0)$とし、座標平面上の曲線y=f(x)をCとする。ただし、logxは自然対数を表す。関数f(x)は$x=\fbox{あ}$で最小値をとる。曲線C上の点A(1,f(1))における曲線Cの接線をlとすると、lの方程式は$y=\fbox{い}$である。
曲線Cと接線lおよび直線x=2で囲まれた図形の面積は$\fbox{う}$である。また、点$(t,f(t))(t \lt1)$をPとし、点Aから点Pまでの曲線Cの長さをL(t)とすると$L(2)=\fbox{え}$である。また、$\displaystyle \lim_{ t \to 1+0 } \dfrac{L(t)}{t-1}= \fbox{お}$である。
2023明治大学理工学部過去問
この動画を見る
$f(x)=\dfrac{1}{8}x^2-logx(x \gt0)$とし、座標平面上の曲線y=f(x)をCとする。ただし、logxは自然対数を表す。関数f(x)は$x=\fbox{あ}$で最小値をとる。曲線C上の点A(1,f(1))における曲線Cの接線をlとすると、lの方程式は$y=\fbox{い}$である。
曲線Cと接線lおよび直線x=2で囲まれた図形の面積は$\fbox{う}$である。また、点$(t,f(t))(t \lt1)$をPとし、点Aから点Pまでの曲線Cの長さをL(t)とすると$L(2)=\fbox{え}$である。また、$\displaystyle \lim_{ t \to 1+0 } \dfrac{L(t)}{t-1}= \fbox{お}$である。
2023明治大学理工学部過去問
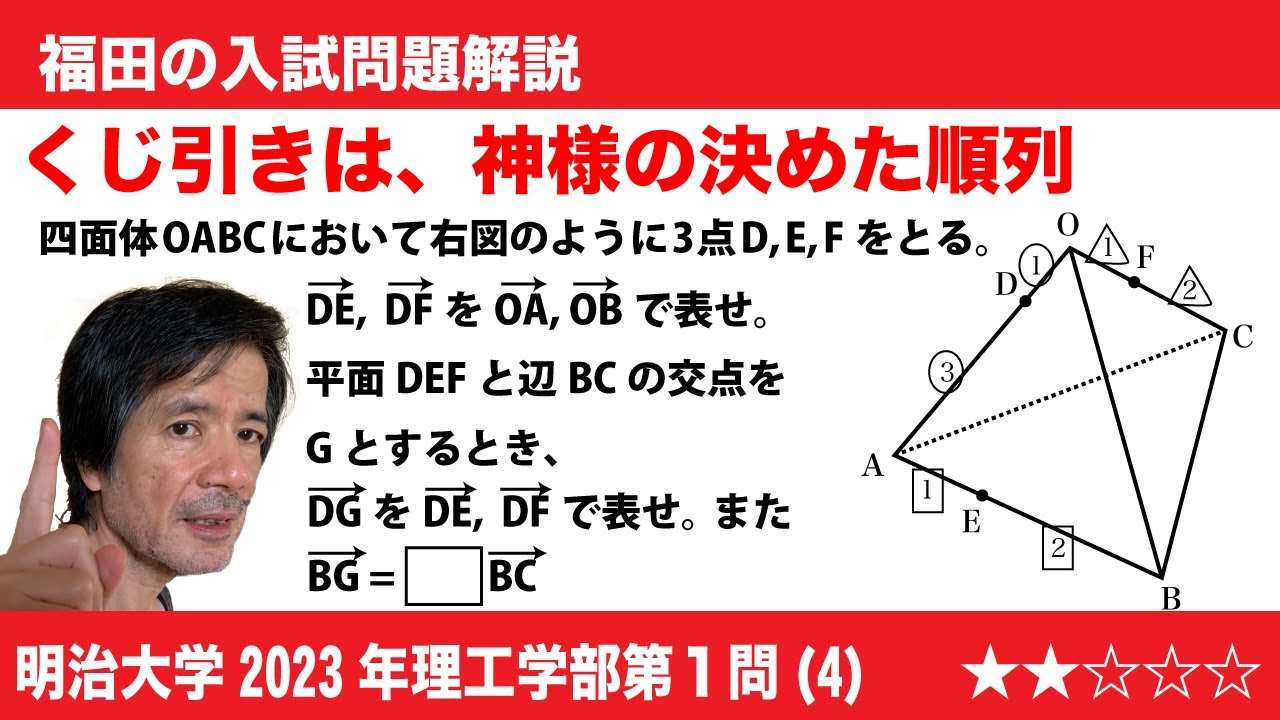
福田の数学〜空間の位置ベクトルの考え方〜明治大学2023年理工学部第1問(4)〜平面と直線の交点の位置ベクトル
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (4)四面体OABCにおいて、辺OAを1:3に内分する点をD、辺ABを1:2に内分する点をE、辺OCを1:2に内分する点をFとすると、
$\overrightarrow{DE}$=$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハヒ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\overrightarrow{OB}$, $\overrightarrow{DF}$=$-\frac{\boxed{\ \ ホ\ \ }}{\boxed{\ \ マ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ ミ\ \ }}{\boxed{\ \ ム\ \ }}\overrightarrow{OC}$
である。さらに、3点D,E,Fを通る平面と辺BCの交点をGとすると、
$\overrightarrow{DF}$=$\frac{\boxed{\ \ メ\ \ }}{\boxed{\ \ モ\ \ }}\overrightarrow{DE}$+$\frac{\boxed{\ \ ヤ\ \ }}{\boxed{\ \ ユ\ \ }}\overrightarrow{DF}$
である。したがって、$\overrightarrow{BG}$=$\frac{\boxed{\ \ ヨ\ \ }}{\boxed{\ \ ラ\ \ }}\overrightarrow{BC}$ となる。
この動画を見る
$\Large{\boxed{1}}$ (4)四面体OABCにおいて、辺OAを1:3に内分する点をD、辺ABを1:2に内分する点をE、辺OCを1:2に内分する点をFとすると、
$\overrightarrow{DE}$=$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハヒ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\overrightarrow{OB}$, $\overrightarrow{DF}$=$-\frac{\boxed{\ \ ホ\ \ }}{\boxed{\ \ マ\ \ }}\overrightarrow{OA}$+$\frac{\boxed{\ \ ミ\ \ }}{\boxed{\ \ ム\ \ }}\overrightarrow{OC}$
である。さらに、3点D,E,Fを通る平面と辺BCの交点をGとすると、
$\overrightarrow{DF}$=$\frac{\boxed{\ \ メ\ \ }}{\boxed{\ \ モ\ \ }}\overrightarrow{DE}$+$\frac{\boxed{\ \ ヤ\ \ }}{\boxed{\ \ ユ\ \ }}\overrightarrow{DF}$
である。したがって、$\overrightarrow{BG}$=$\frac{\boxed{\ \ ヨ\ \ }}{\boxed{\ \ ラ\ \ }}\overrightarrow{BC}$ となる。
福田の数学〜くじ引きは神様が決めた順列〜明治大学2023年理工学部第1問(3)〜くじ引きの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)当たりくじ4本とはずれくじ6本からなる10本のくじがある。この中からAが2本のくじを同時に引き、その後Bが2本のくじを同時に引く。ただし、Aが引いたくじは元には戻さないものとする。
(a)Aの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。
(b)AとBが引いたくじの中に1本も当たりがない確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(c)Aが引いたくじのうち1本だけが当たりで、かつBが引いたくじのうち1本だけが当たりである確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(d)Bの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌネ\ \ }}$である。
この動画を見る
$\Large{\boxed{1}}$ (3)当たりくじ4本とはずれくじ6本からなる10本のくじがある。この中からAが2本のくじを同時に引き、その後Bが2本のくじを同時に引く。ただし、Aが引いたくじは元には戻さないものとする。
(a)Aの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。
(b)AとBが引いたくじの中に1本も当たりがない確率は$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツテ\ \ }}$である。
(c)Aが引いたくじのうち1本だけが当たりで、かつBが引いたくじのうち1本だけが当たりである確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(d)Bの引いたくじが2本とも当たりである確率は$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌネ\ \ }}$である。
福田の数学〜相反方程式の扱い方を知っていますか〜明治大学2023年理工学部第1問(2)〜相反方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)(a)$t$を実数とする。$x$についての方程式$x$+$\frac{1}{x}$=$t$ が実数解をもつための必要十分条件は$t$≦$-\boxed{\ \ カ\ \ }$または$t$≧$\boxed{\ \ キ\ \ }$ である。
(b)$k$を実数と定数とし、$f(x)$=$7x^4$+$2x^3$+$kx^2$+$2x$+7 とする。
$x$=$a$が$f(x)$=0 の解であるとき、$t$=$a$+$\frac{1}{a}$ とおくと
$\boxed{\ \ ク\ \ }t^2$+$\boxed{\ \ ケ\ \ }t$+$(k-\boxed{\ \ コサ\ \ })$=0
が成り立つ。方程式$f(x)$=0 の異なる実数解の個数が3個となるような$k$の値は$k$=$-\boxed{\ \ シス\ \ }$ である。
この動画を見る
$\Large{\boxed{1}}$ (2)(a)$t$を実数とする。$x$についての方程式$x$+$\frac{1}{x}$=$t$ が実数解をもつための必要十分条件は$t$≦$-\boxed{\ \ カ\ \ }$または$t$≧$\boxed{\ \ キ\ \ }$ である。
(b)$k$を実数と定数とし、$f(x)$=$7x^4$+$2x^3$+$kx^2$+$2x$+7 とする。
$x$=$a$が$f(x)$=0 の解であるとき、$t$=$a$+$\frac{1}{a}$ とおくと
$\boxed{\ \ ク\ \ }t^2$+$\boxed{\ \ ケ\ \ }t$+$(k-\boxed{\ \ コサ\ \ })$=0
が成り立つ。方程式$f(x)$=0 の異なる実数解の個数が3個となるような$k$の値は$k$=$-\boxed{\ \ シス\ \ }$ である。
福田の数学〜微分可能である条件とは何か〜明治大学2023年理工学部第1問(1)〜微分可能であるための条件

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)$a$,$b$,$c$を実数の定数とし、関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
\displaystyle\frac{1+3x-a\cos 2x}{4x} (x>0)\\
bx+c (x≦0)\\
\end{array}\right.$
で定める。$f(x)$が$x$=0で微分可能であるとき
$a$=$\boxed{\ \ ア\ \ }$, $b$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$, $c$=$\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。
この動画を見る
$\Large{\boxed{1}}$ (1)$a$,$b$,$c$を実数の定数とし、関数$f(x)$を
$f(x)$=$\left\{\begin{array}{1}
\displaystyle\frac{1+3x-a\cos 2x}{4x} (x>0)\\
bx+c (x≦0)\\
\end{array}\right.$
で定める。$f(x)$が$x$=0で微分可能であるとき
$a$=$\boxed{\ \ ア\ \ }$, $b$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$, $c$=$\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。
福田の数学〜陰関数を考える貴重な問題〜明治大学2023年全学部統一Ⅲ第4問〜陰関数のグラフの増減とグラフ

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
この動画を見る
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
福田の数学〜双曲線と直線の位置関係を考えよう〜明治大学2023年全学部統一Ⅲ第3問〜双曲線と直線

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
この動画を見る
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
福田の数学〜部分積分と極限のコンボ〜明治大学2023年全学部統一Ⅲ第2問〜部分積分と極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ $t$>0 に対して、次の2つの定積分を考える。
$I$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\sin xdx$, $J$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx$
部分積分を用いれば$I$=$\boxed{\ \ ア\ \ }$-$tJ$, $J$=$\boxed{\ \ イ\ \ }$+$tI$ が成り立つことが分かるので、
$I$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$, $J$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ エ\ \ }}$
を得る。したがって、$\displaystyle\lim_{t \to \infty}\frac{\log\boxed{\ \ エ\ \ }}{t}$=0 を用いれば、
$\displaystyle\lim_{t \to \infty}\frac{1}{t}\log\left(\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx-\frac{t}{\boxed{\ \ エ\ \ }}\right)$=$\boxed{\ \ カ\ \ }$
となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ ウ\ \ }$の解答群
⓪-1 ①1 ②2-$\pi$ ③$\pi$ ④1-$t$ ⑤1+$t$
⑥1-$t^2$ ⑦1+$t^2$ ⑧$-e^{-\frac{\pi}{2}t}$ ⑨$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ ウ\ \ }$、$\boxed{\ \ オ\ \ }$の解答群
⓪$t$ ①1 ②-1$-te^{-\frac{\pi}{2}t}$ ③-1$+te^{-\frac{\pi}{2}t}$ ④1$-te^{-\frac{\pi}{2}t}$
⑤1$+te^{-\frac{\pi}{2}t}$ ⑥-$t$-$e^{-\frac{\pi}{2}t}$ ⑦-$t$+$e^{-\frac{\pi}{2}t}$ ⑧$t$-$e^{-\frac{\pi}{2}t}$ ⑨$t$+$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ カ\ \ }$の解答群
⓪0 ①$-\frac{\pi}{2}$ ②$-\frac{\pi}{3}$ ③$-\frac{\pi}{4}$ ④$-\frac{\pi}{6}$ ⑤$-\frac{\pi}{12}$ ⑥$\frac{\pi}{6}$
⑦$\frac{\pi}{4}$ ⑧$\frac{\pi}{3}$ ⑨$\frac{\pi}{2}$
この動画を見る
$\Large{\boxed{2}}$ $t$>0 に対して、次の2つの定積分を考える。
$I$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\sin xdx$, $J$=$\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx$
部分積分を用いれば$I$=$\boxed{\ \ ア\ \ }$-$tJ$, $J$=$\boxed{\ \ イ\ \ }$+$tI$ が成り立つことが分かるので、
$I$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$, $J$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ エ\ \ }}$
を得る。したがって、$\displaystyle\lim_{t \to \infty}\frac{\log\boxed{\ \ エ\ \ }}{t}$=0 を用いれば、
$\displaystyle\lim_{t \to \infty}\frac{1}{t}\log\left(\displaystyle\int_0^{\frac{\pi}{2}}e^{-tx}\cos xdx-\frac{t}{\boxed{\ \ エ\ \ }}\right)$=$\boxed{\ \ カ\ \ }$
となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ ウ\ \ }$の解答群
⓪-1 ①1 ②2-$\pi$ ③$\pi$ ④1-$t$ ⑤1+$t$
⑥1-$t^2$ ⑦1+$t^2$ ⑧$-e^{-\frac{\pi}{2}t}$ ⑨$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ ウ\ \ }$、$\boxed{\ \ オ\ \ }$の解答群
⓪$t$ ①1 ②-1$-te^{-\frac{\pi}{2}t}$ ③-1$+te^{-\frac{\pi}{2}t}$ ④1$-te^{-\frac{\pi}{2}t}$
⑤1$+te^{-\frac{\pi}{2}t}$ ⑥-$t$-$e^{-\frac{\pi}{2}t}$ ⑦-$t$+$e^{-\frac{\pi}{2}t}$ ⑧$t$-$e^{-\frac{\pi}{2}t}$ ⑨$t$+$e^{-\frac{\pi}{2}t}$
$\boxed{\ \ カ\ \ }$の解答群
⓪0 ①$-\frac{\pi}{2}$ ②$-\frac{\pi}{3}$ ③$-\frac{\pi}{4}$ ④$-\frac{\pi}{6}$ ⑤$-\frac{\pi}{12}$ ⑥$\frac{\pi}{6}$
⑦$\frac{\pi}{4}$ ⑧$\frac{\pi}{3}$ ⑨$\frac{\pi}{2}$
福田の数学〜zを正負で場合分けできないときどうする〜明治大学2023年全学部統一Ⅲ第1問(2)〜複素数に関する2次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)複素数$z$の方程式
$z^2$-3|$z$|+2=0
を考える。この方程式は$\boxed{\ \ イ\ \ }$個の解を持ち、このうち実数でないかの個数は$\boxed{\ \ ウ\ \ }$個である。
この動画を見る
$\Large{\boxed{1}}$ (2)複素数$z$の方程式
$z^2$-3|$z$|+2=0
を考える。この方程式は$\boxed{\ \ イ\ \ }$個の解を持ち、このうち実数でないかの個数は$\boxed{\ \ ウ\ \ }$個である。
福田の数学〜無限級数の和は部分和の極限〜明治大学2023年全学部統一Ⅲ第1問(1)〜無限級数の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
無限級数
$\displaystyle \sum_{n=1}^{\infty} \log \frac{(n+1)(n+2)}{n(n+3)}$
の和を求めよ。
2023明治大学過去問
この動画を見る
無限級数
$\displaystyle \sum_{n=1}^{\infty} \log \frac{(n+1)(n+2)}{n(n+3)}$
の和を求めよ。
2023明治大学過去問
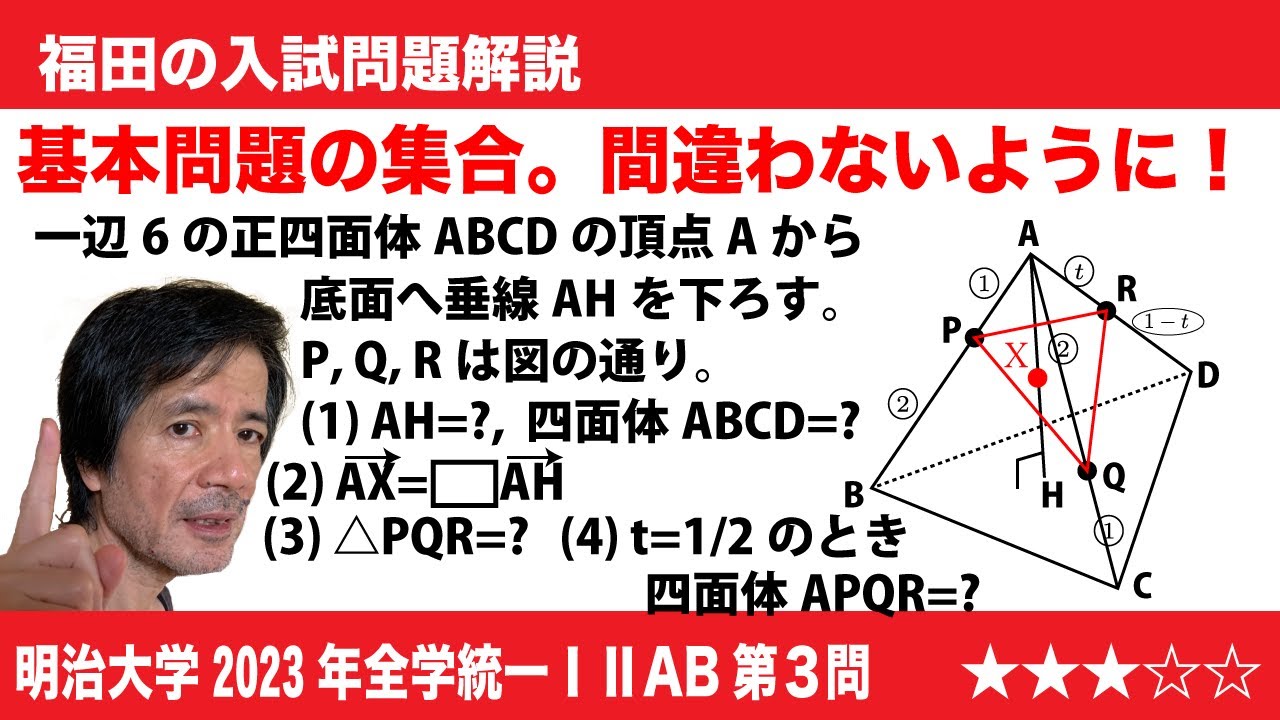
福田の数学〜共通テスト対策にもってこい〜明治大学2023年全学部統一ⅠⅡAB第3問〜四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#共通テスト#空間における垂直と平行と多面体(オイラーの法則)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
福田の数学〜微分積分の基本問題〜明治大学2023年全学部統一ⅠⅡAB第2問〜関数の増減と3次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ $k$を正の実数とし、$x$の関数$f(x)$を
$f(x)$=$x^3$$-3kx^2$$+9(k^2+2k-3)$
により定める。関数$f(x)$は$x$=$\boxed{\ \ ア\ \ }$で極大値$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$をとり、
$x$=$\boxed{\ \ キ\ \ }$で極小値$-\boxed{\ \ ク\ \ }k^3$+$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$ をとる。
以下、$f(x)$の極小値が0になる$k$の値を$a$,$b$(ただし、$a$<$b$)、$f(x)$の極大値が0となる$k$の値を$c$とする。このとき、
$a$=$\displaystyle\frac{\boxed{\ \ ケ\ \ }\left(\sqrt{\boxed{\ \ コサ\ \ }}-\boxed{\ \ シ\ \ }\right)}{\boxed{\ \ ス\ \ }}$, $b$=$\boxed{\ \ セ\ \ }$, $c$=$\boxed{\ \ ソ\ \ }$
である。座標平面において、$k$=$\boxed{\ \ セ\ \ }$のとき、$x$軸の$x$≧0の部分と$y$軸の$y$≧0 の部分と$y$=$f(x)$のグラフとで囲まれた図形の面積は$\boxed{\ \ タチツ\ \ }$である。
方程式$f(x)$=0 が異なる3つの実数解を持つための必要十分条件は$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ ア\ \ }$, $\boxed{\ \ キ\ \ }$の解答群
⓪0 ①$\frac{k}{2}$ ②$\frac{2k}{3}$ ③$k$ ④$\frac{4k}{3}$
⑤$2k$ ⑥$-\frac{k}{2}$ ⑦$-\frac{2k}{3}$ ⑧$-k$ ⑨$-2k$
$\boxed{\ \ テ\ \ }$の解答群
⓪$k$<$a$, $b$<$k$<$c$ ①$k$<$a$, $c$<$k$<$b$ ②$k$<$c$, $a$<$k$<$b$
③$a$<$k$<$b$, $c$<$k$ ④$a$<$k$<$c$, $b$<$k$ ⑤$c$<$k$<$a$, $b$<$k$
⑥$a$<$k$<$c$ ⑦$c$<$k$<$a$ ⑧$b$<$k$<$c$ ⑨$c$<$k$<$b$
この動画を見る
$\Large{\boxed{1}}$ $k$を正の実数とし、$x$の関数$f(x)$を
$f(x)$=$x^3$$-3kx^2$$+9(k^2+2k-3)$
により定める。関数$f(x)$は$x$=$\boxed{\ \ ア\ \ }$で極大値$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$をとり、
$x$=$\boxed{\ \ キ\ \ }$で極小値$-\boxed{\ \ ク\ \ }k^3$+$\boxed{\ \ イ\ \ }k^2$+$\boxed{\ \ ウエ\ \ }k$-$\boxed{\ \ オカ\ \ }$ をとる。
以下、$f(x)$の極小値が0になる$k$の値を$a$,$b$(ただし、$a$<$b$)、$f(x)$の極大値が0となる$k$の値を$c$とする。このとき、
$a$=$\displaystyle\frac{\boxed{\ \ ケ\ \ }\left(\sqrt{\boxed{\ \ コサ\ \ }}-\boxed{\ \ シ\ \ }\right)}{\boxed{\ \ ス\ \ }}$, $b$=$\boxed{\ \ セ\ \ }$, $c$=$\boxed{\ \ ソ\ \ }$
である。座標平面において、$k$=$\boxed{\ \ セ\ \ }$のとき、$x$軸の$x$≧0の部分と$y$軸の$y$≧0 の部分と$y$=$f(x)$のグラフとで囲まれた図形の面積は$\boxed{\ \ タチツ\ \ }$である。
方程式$f(x)$=0 が異なる3つの実数解を持つための必要十分条件は$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ ア\ \ }$, $\boxed{\ \ キ\ \ }$の解答群
⓪0 ①$\frac{k}{2}$ ②$\frac{2k}{3}$ ③$k$ ④$\frac{4k}{3}$
⑤$2k$ ⑥$-\frac{k}{2}$ ⑦$-\frac{2k}{3}$ ⑧$-k$ ⑨$-2k$
$\boxed{\ \ テ\ \ }$の解答群
⓪$k$<$a$, $b$<$k$<$c$ ①$k$<$a$, $c$<$k$<$b$ ②$k$<$c$, $a$<$k$<$b$
③$a$<$k$<$b$, $c$<$k$ ④$a$<$k$<$c$, $b$<$k$ ⑤$c$<$k$<$a$, $b$<$k$
⑥$a$<$k$<$c$ ⑦$c$<$k$<$a$ ⑧$b$<$k$<$c$ ⑨$c$<$k$<$b$
