学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜上智大学2024TEAP利用型文系第1問〜正四面体に関する図形問題
単元：
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
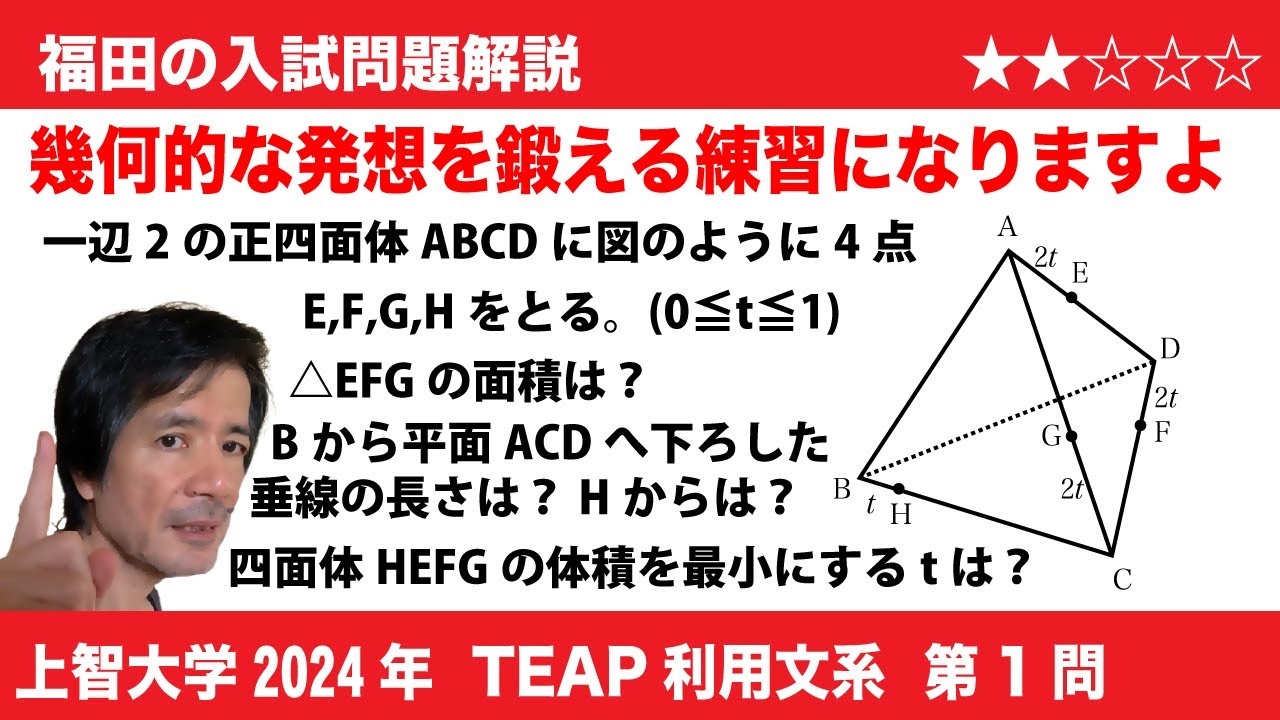
$1$ 辺の長さが $2$ の正四面体 $\mathrm{ABCD}$ において、辺 $\mathrm{AD}$ 上の点 $\mathrm{E}$、辺 $\mathrm{DC}$ 上の点 $\mathrm{F}$、辺 $\mathrm{CA}$ 上の点 $\mathrm{G}$、辺 $\mathrm{BC}$ 上の点 $\mathrm{H}$ を$\mathrm{AE}$$=\mathrm{DF}$$=\mathrm{CG}$$=2t,$ $\mathrm{BH}=t$ となるようにとる。ただし、 $0 \leqq t \leqq 1$ とする。
$(1)$ $\triangle \mathrm{EFG}$ の面積は $\sqrt{\fbox{ア}}(\fbox{イ}t^2$$+\fbox{ウ}t$$+\fbox{エ})$ である。
$(2)$ $\mathrm{B}$ から平面 $\mathrm{ACD}$ に垂線を下ろし、平面 $\mathrm{ACD}$ との交点を $\mathrm{P}$ とするとき、 $\mathrm{BP} = \frac{\fbox{オ}}{\fbox{カ}}\sqrt{\fbox{キ}}$ である。
$(3)$ $\mathrm{H}$ から平面 $\mathrm{EFG}$ に垂線を下ろし、平面 $\mathrm{EFG}$ との交点を $\mathrm{Q}$ とするとき、 $\mathrm{HQ} = \frac{\fbox{ク}}{\fbox{ケ}}\sqrt{\fbox{コ}}(t+\fbox{サ})$ である。
$(4)$ 四面体 $\mathrm{HEFG}$ の体積が最小になるのは
$t=\fbox{シ} + \frac{\fbox{ス}}{\fbox{セ}}\sqrt{\fbox{ソ}}$
この動画を見る
$1$ 辺の長さが $2$ の正四面体 $\mathrm{ABCD}$ において、辺 $\mathrm{AD}$ 上の点 $\mathrm{E}$、辺 $\mathrm{DC}$ 上の点 $\mathrm{F}$、辺 $\mathrm{CA}$ 上の点 $\mathrm{G}$、辺 $\mathrm{BC}$ 上の点 $\mathrm{H}$ を$\mathrm{AE}$$=\mathrm{DF}$$=\mathrm{CG}$$=2t,$ $\mathrm{BH}=t$ となるようにとる。ただし、 $0 \leqq t \leqq 1$ とする。
$(1)$ $\triangle \mathrm{EFG}$ の面積は $\sqrt{\fbox{ア}}(\fbox{イ}t^2$$+\fbox{ウ}t$$+\fbox{エ})$ である。
$(2)$ $\mathrm{B}$ から平面 $\mathrm{ACD}$ に垂線を下ろし、平面 $\mathrm{ACD}$ との交点を $\mathrm{P}$ とするとき、 $\mathrm{BP} = \frac{\fbox{オ}}{\fbox{カ}}\sqrt{\fbox{キ}}$ である。
$(3)$ $\mathrm{H}$ から平面 $\mathrm{EFG}$ に垂線を下ろし、平面 $\mathrm{EFG}$ との交点を $\mathrm{Q}$ とするとき、 $\mathrm{HQ} = \frac{\fbox{ク}}{\fbox{ケ}}\sqrt{\fbox{コ}}(t+\fbox{サ})$ である。
$(4)$ 四面体 $\mathrm{HEFG}$ の体積が最小になるのは
$t=\fbox{シ} + \frac{\fbox{ス}}{\fbox{セ}}\sqrt{\fbox{ソ}}$
#京都帝国大学1935#不定積分_60
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^2}}dx$を解け.
1935京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^2}}dx$を解け.
1935京都帝国大学過去問題
#京都大学1937#極限_59
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
霊感強い系の受験者は、山勘でいける 関西医科大学2024 大学入試問題#933
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#数B#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
数列$\{an\}$を
$a_1=2,a_{n+1}=S_n-n(n-4)$
$(n=1,2,3･･･)$で定めるとき,$a_n$と$S_n$を
それぞれ$n$の式で表せ.
2024関西医科大学過去問題
この動画を見る
数列$\{an\}$を
$a_1=2,a_{n+1}=S_n-n(n-4)$
$(n=1,2,3･･･)$で定めるとき,$a_n$と$S_n$を
それぞれ$n$の式で表せ.
2024関西医科大学過去問題
#弘前大学2023#定積分_58
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
#弘前大学2023#定積分_57
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
京大らしさ全開の不朽の名作 京都帝国大学1937 大学入試問題#932
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
#弘前大学2024#定積分_56
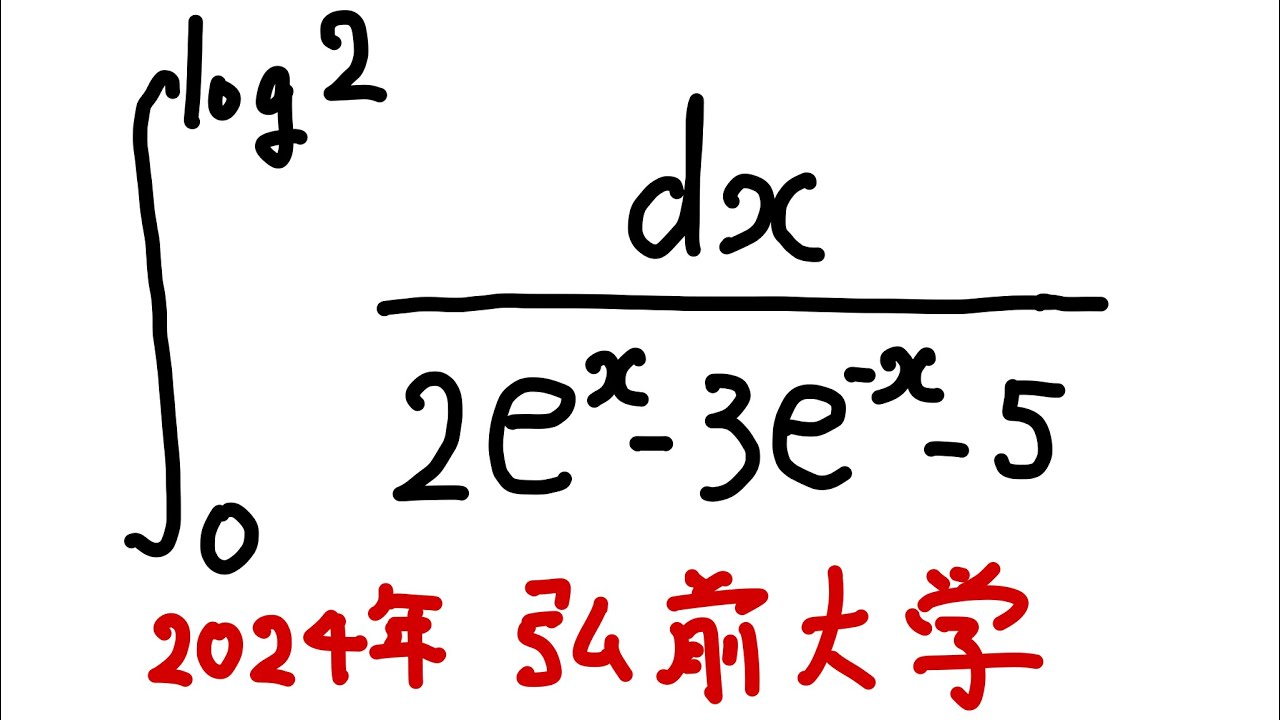
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
この動画を見る
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
#京都帝国大学1937#微分_55
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$y=e^{x^x}$なるとき,
$\dfrac{dy}{dx}$を求めよ.
1937京都帝国大学過去問題
この動画を見る
$y=e^{x^x}$なるとき,
$\dfrac{dy}{dx}$を求めよ.
1937京都帝国大学過去問題
沼に嵌りそうな典型問題 産業医科大学2019 大学入試問題#931
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が
$x^2+y^2+2xy+2x-2y+2=0$を満たすとき,
$x-y$の最大値を求めよ.
2019産業医科大学過去問題
この動画を見る
実数$x,y$が
$x^2+y^2+2xy+2x-2y+2=0$を満たすとき,
$x-y$の最大値を求めよ.
2019産業医科大学過去問題
福田の数学〜青山学院大学2024理工学部第3問〜2次方程式の解の条件と領域
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
福田次郎
問題文全文(内容文)：
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
この動画を見る
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
#京都大学1937#不定積分_54
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^6}}dx$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^6}}dx$を解け.
1937京都帝国大学過去問題
#電気通信大学2024#不定積分_53
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} e^x \sqrt{6-e^x} dx$を解け.
2024電気通信大学過去問題
この動画を見る
$\displaystyle \int_{}^{} e^x \sqrt{6-e^x} dx$を解け.
2024電気通信大学過去問題
突破口を探す不定積分 京都帝国大学1936 大学入試問題#931
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$ \sec \ x=\dfrac{1}{\cos x}$とする.
$\displaystyle \int_{}^{} \sec \ x \ \tan^2 x \ dx$を解け.
1936京都帝国大学過去問題
この動画を見る
$ \sec \ x=\dfrac{1}{\cos x}$とする.
$\displaystyle \int_{}^{} \sec \ x \ \tan^2 x \ dx$を解け.
1936京都帝国大学過去問題
福田の数学〜青山学院大学2024理工学部第2問〜法線と面積と回転体の体積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=\tan{x}$とする。また、曲線
$\displaystyle C:y=f(x)(-\frac{\pi}{2}\lt x\lt \frac{\pi}{2})$
上の点$(\displaystyle \frac{\pi}{6},f(\frac{\pi}{6}))$における法線を$\ell$とする。
(1)法線$\ell$の方程式は$\displaystyle y=\frac{\fbox{アイ}}{\fbox{ウ}}x+\frac{\fbox{エ}}{\fbox{オ}}\pi+\frac{\sqrt{\fbox{カ}}}{\fbox{キ}}である。$
(2)曲線$C$と$x$軸および法線$\ell$で囲まれた図形の面積は
$\log{a}+b(a=\frac{\fbox{ク}\sqrt{\fbox{ケ}}}{\fbox{コ}},b=\frac{\fbox{サ}}{\fbox{シ}})$
この動画を見る
$f(x)=\tan{x}$とする。また、曲線
$\displaystyle C:y=f(x)(-\frac{\pi}{2}\lt x\lt \frac{\pi}{2})$
上の点$(\displaystyle \frac{\pi}{6},f(\frac{\pi}{6}))$における法線を$\ell$とする。
(1)法線$\ell$の方程式は$\displaystyle y=\frac{\fbox{アイ}}{\fbox{ウ}}x+\frac{\fbox{エ}}{\fbox{オ}}\pi+\frac{\sqrt{\fbox{カ}}}{\fbox{キ}}である。$
(2)曲線$C$と$x$軸および法線$\ell$で囲まれた図形の面積は
$\log{a}+b(a=\frac{\fbox{ク}\sqrt{\fbox{ケ}}}{\fbox{コ}},b=\frac{\fbox{サ}}{\fbox{シ}})$
#京都帝国大学1935#不定積分_52
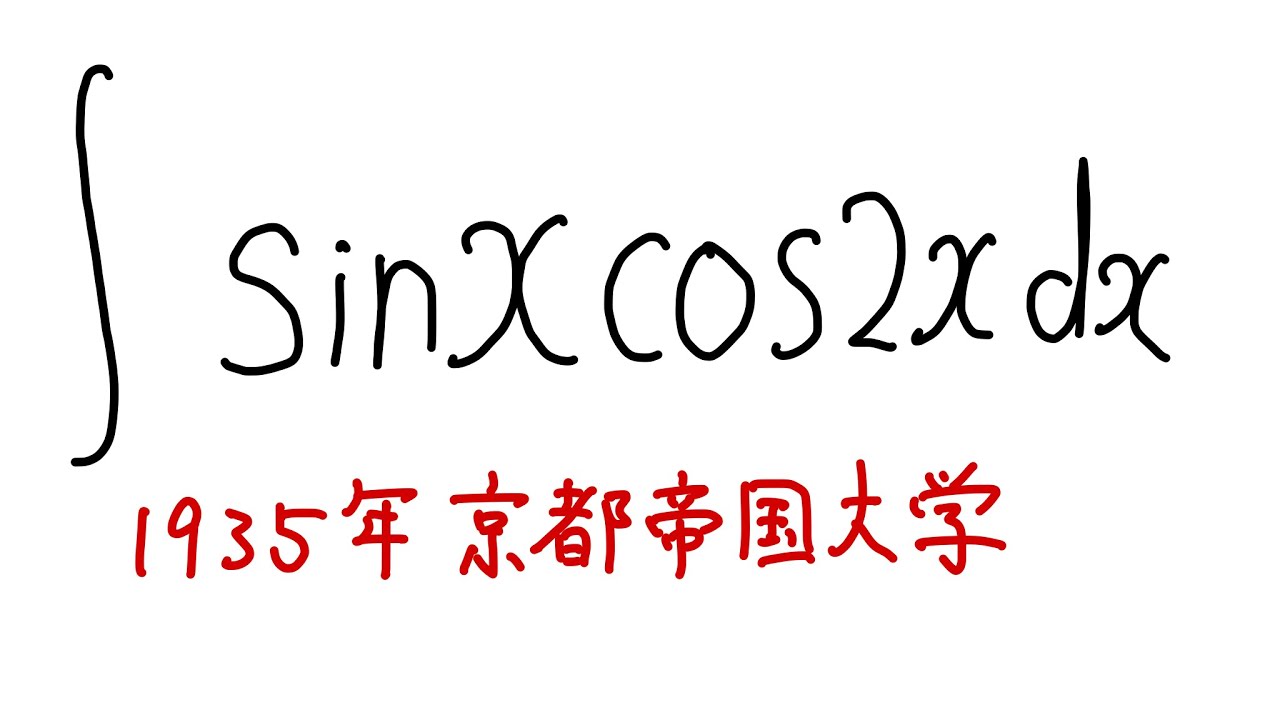
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \sin x \ \cos 2x \ dx$を解け.
1935京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \sin x \ \cos 2x \ dx$を解け.
1935京都帝国大学過去問題
#京都帝国大学1937#不定積分_51
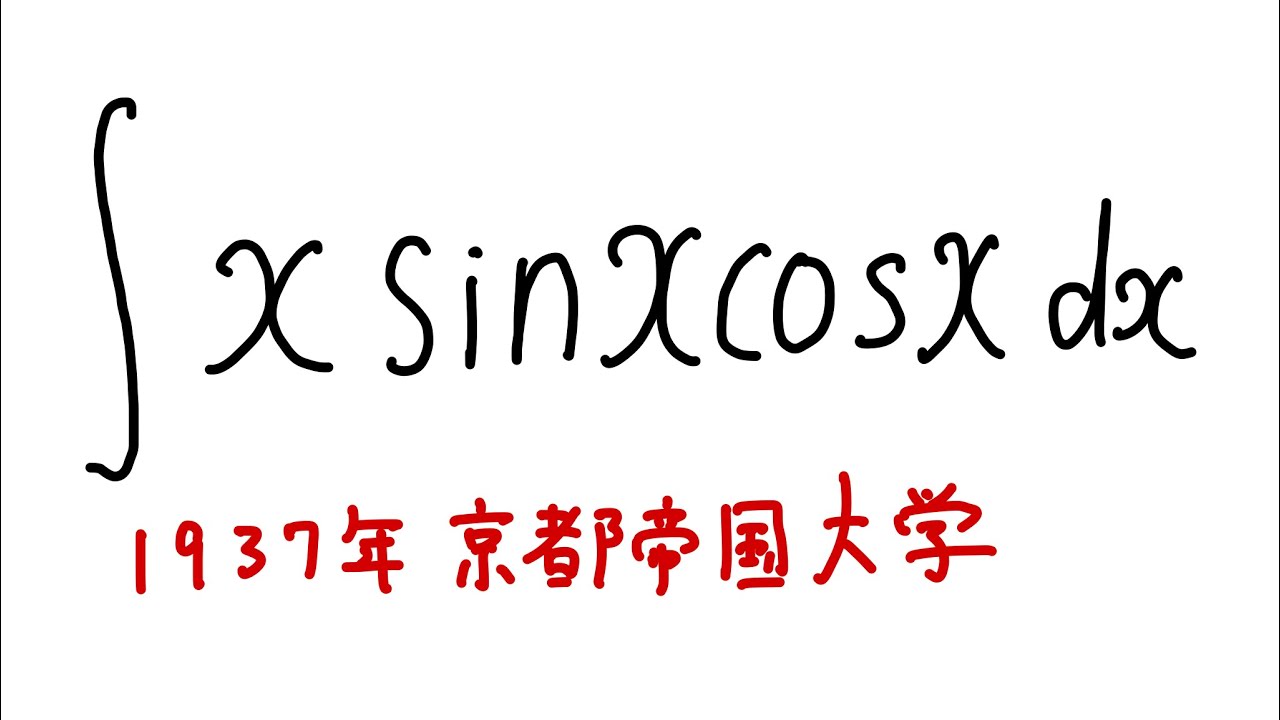
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x \ \sin x\ \cos x \ dx$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \sin x\ \cos x \ dx$を解け.
1937京都帝国大学過去問題
定積分の微分の基本問題 島根大学後期2024 大学入試問題#930
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学
指導講師：
ますただ
問題文全文(内容文)：
$a$の正の定数とする.
関数$g(x)$が,$x\gt 0$で定義された連続関数で,
次の等式をみたすとき,$g(x)$と$a$の値を求めよ.
$\displaystyle \int_{a}^{x^3} g(u) du =\log x$
2024島根大学後期過去問題
この動画を見る
$a$の正の定数とする.
関数$g(x)$が,$x\gt 0$で定義された連続関数で,
次の等式をみたすとき,$g(x)$と$a$の値を求めよ.
$\displaystyle \int_{a}^{x^3} g(u) du =\log x$
2024島根大学後期過去問題
#三重大学医学部2023#極限_50
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
#三重大学医学部2023#不定積分_49
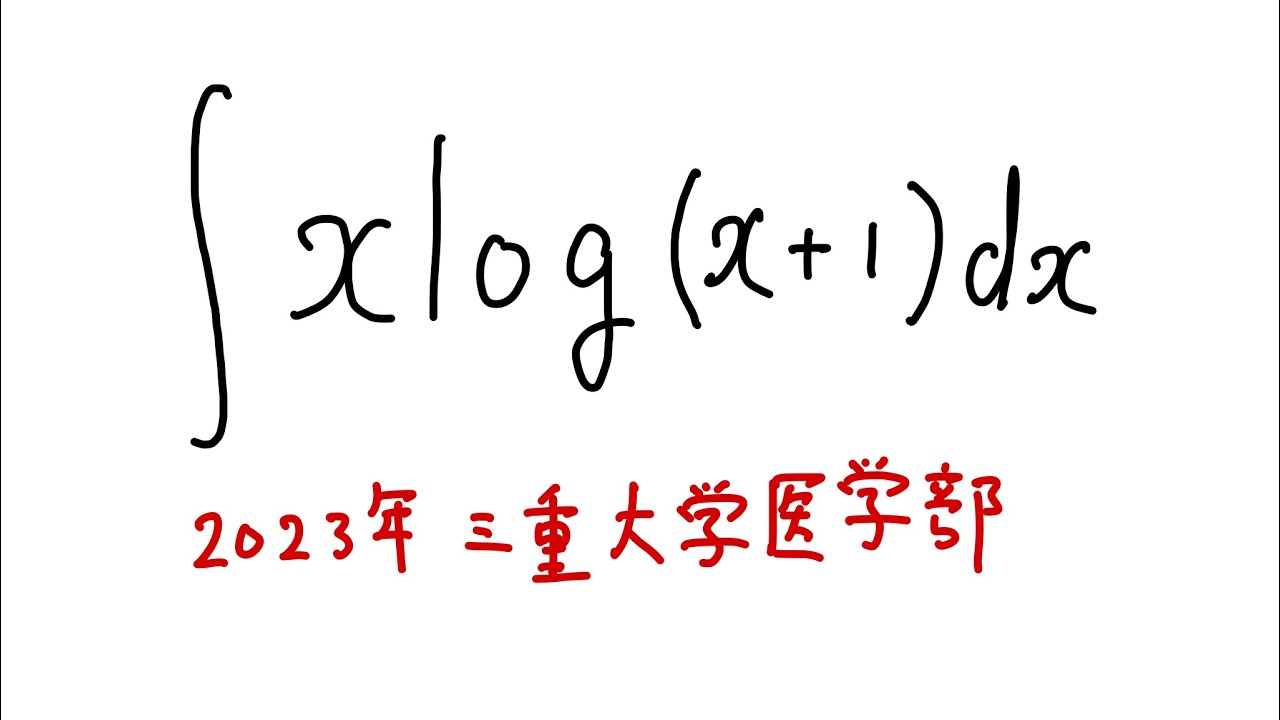
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
戦後の京都大学の入試いけんじゃね？ 京都大学医学部1946 大学入試問題#929
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^4-17x^2-34x-30=0$
なる方程式を解け.
1946京都大学医学部過去問題
この動画を見る
$x^4-17x^2-34x-30=0$
なる方程式を解け.
1946京都大学医学部過去問題
福田の数学〜明治大学2024理工学部第3問〜放物線と折れ線の位置関係
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
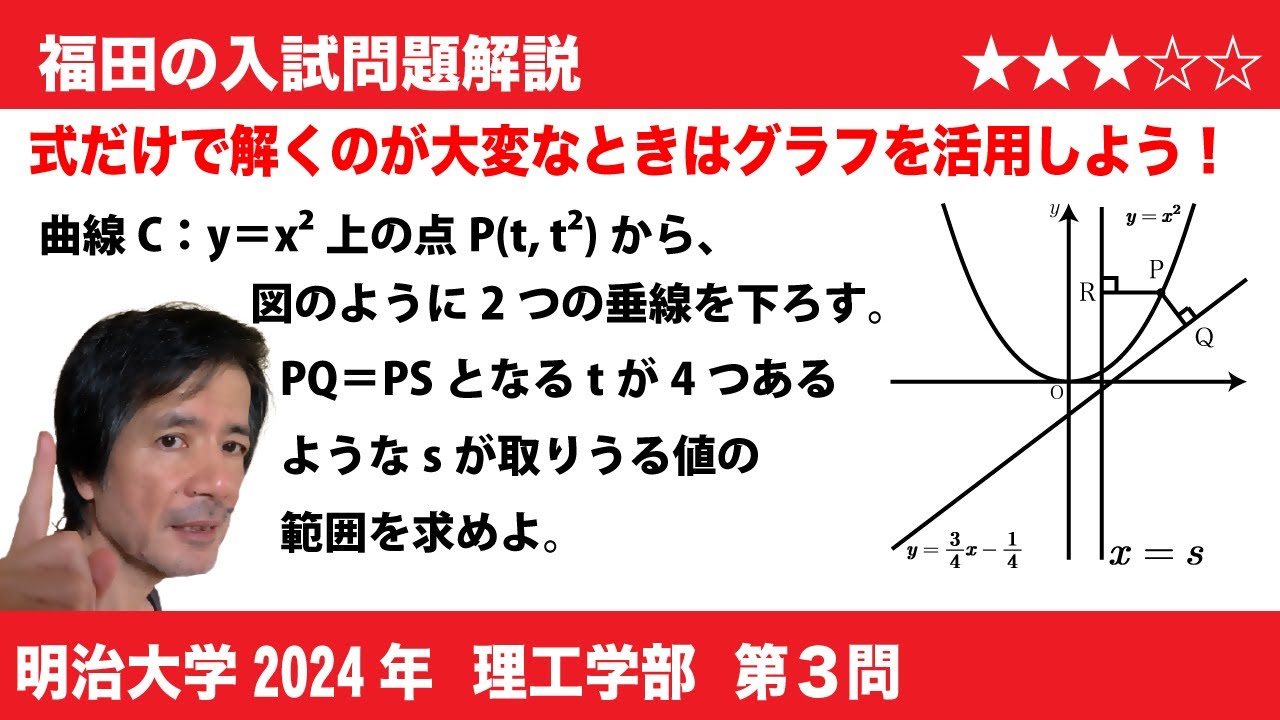
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
この動画を見る
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
#明治大学2023#極限_48
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
この動画を見る
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
#三重大学医学部2023#不定積分_47
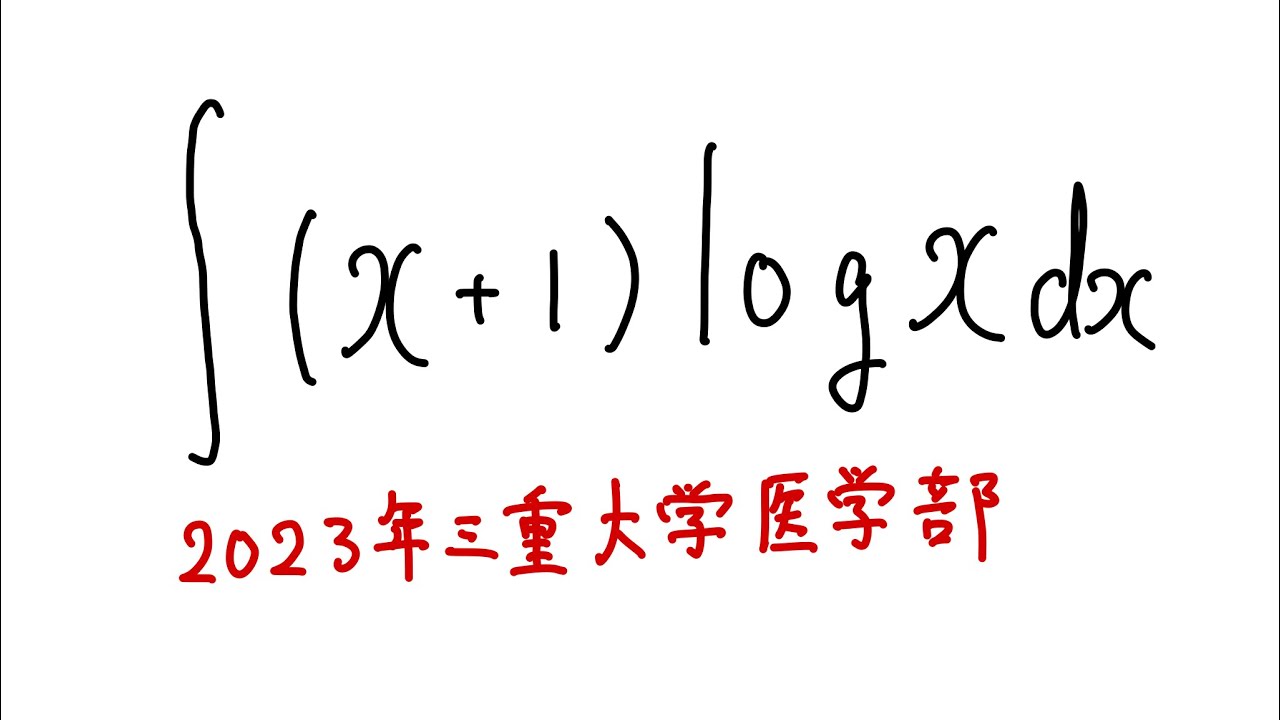
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} (x+1)\log x \ dx$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} (x+1)\log x \ dx$
を解け.
2023三重大学医学部過去問題
至高かつ王道の整数問題 関西医科大学2019 大学入試問題#928
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
正の整数の組$(x,y,z)$が
$2x^2+2y^2+z^2+2xy-2xz-2yz=9$を満たすとき
$x+y+z$の最大値を求めよ.
2019関西医科大学過去問題
この動画を見る
正の整数の組$(x,y,z)$が
$2x^2+2y^2+z^2+2xy-2xz-2yz=9$を満たすとき
$x+y+z$の最大値を求めよ.
2019関西医科大学過去問題
福田の数学〜明治大学2024理工学部第2問〜三角関数の増減と面積
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
この動画を見る
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
#産業医科大学2024#定積分_46
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} \sqrt{3-x^2+2x}\ dx$
を解け.
2024産業医科大学過去問題
この動画を見る
$\displaystyle \int_{-1}^{1} \sqrt{3-x^2+2x}\ dx$
を解け.
2024産業医科大学過去問題
#産業医科大学2023#式変形_45
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{2-\sqrt 3+\sqrt 7}{2+\sqrt 3-\sqrt7}-\dfrac{2+\sqrt 3-\sqrt7}{2-\sqrt3+\sqrt7}$
を簡単にせよ.
2023産業医科大学過去問題
この動画を見る
$\dfrac{2-\sqrt 3+\sqrt 7}{2+\sqrt 3-\sqrt7}-\dfrac{2+\sqrt 3-\sqrt7}{2-\sqrt3+\sqrt7}$
を簡単にせよ.
2023産業医科大学過去問題
王道の整数問題 産業医科大学2024 大学入試問題#927
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{b^2}{a}+\dfrac{a}{b}=6$を満たす
自然数の組$(a,b)$のうち$a+b$の最小値を求めよ.
2024産業医科大学過去問題
この動画を見る
$\dfrac{b^2}{a}+\dfrac{a}{b}=6$を満たす
自然数の組$(a,b)$のうち$a+b$の最小値を求めよ.
2024産業医科大学過去問題
福田の数学〜明治大学2024理工学部第1問(4)〜部屋分けの方法
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$5$ 人の中学生 $\mathrm{A,B,C,D,E}$ と $3$ 人の高校生 $\mathrm{F,G,H}$ の合計 $8$ 人の生徒が、 $2$ つの部屋 $\mathrm{X,Y}$ に分かれて入る。ただし、どの生徒も必ずどちらかの部屋に入るものとする。
(a) どちらの部屋にも $1$ 人以上の生徒が入るような入り方は $\fbox{トナニ}$ 通りである。
(b) どちらの部屋にも $1$ 人以上の中学生が入るような入り方は $\fbox{ヌネノ}$ 通りである。
(c) どちらの部屋にも $1$ 人以上の中学生と $1$ 人以上の高校生が入るような入り方は $\fbox{ハヒフ}$ 通りである。
(d) どちらの部屋も中学生の人数が高校生の人数より多くなるような入り方は $\fbox{ヘホ}$ 通りである。ただし、どちらの部屋にも $1$ 人以上の高校生が入るものとする。
この動画を見る
$5$ 人の中学生 $\mathrm{A,B,C,D,E}$ と $3$ 人の高校生 $\mathrm{F,G,H}$ の合計 $8$ 人の生徒が、 $2$ つの部屋 $\mathrm{X,Y}$ に分かれて入る。ただし、どの生徒も必ずどちらかの部屋に入るものとする。
(a) どちらの部屋にも $1$ 人以上の生徒が入るような入り方は $\fbox{トナニ}$ 通りである。
(b) どちらの部屋にも $1$ 人以上の中学生が入るような入り方は $\fbox{ヌネノ}$ 通りである。
(c) どちらの部屋にも $1$ 人以上の中学生と $1$ 人以上の高校生が入るような入り方は $\fbox{ハヒフ}$ 通りである。
(d) どちらの部屋も中学生の人数が高校生の人数より多くなるような入り方は $\fbox{ヘホ}$ 通りである。ただし、どちらの部屋にも $1$ 人以上の高校生が入るものとする。