学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
疑うところからすべては始まる 聖徳学園
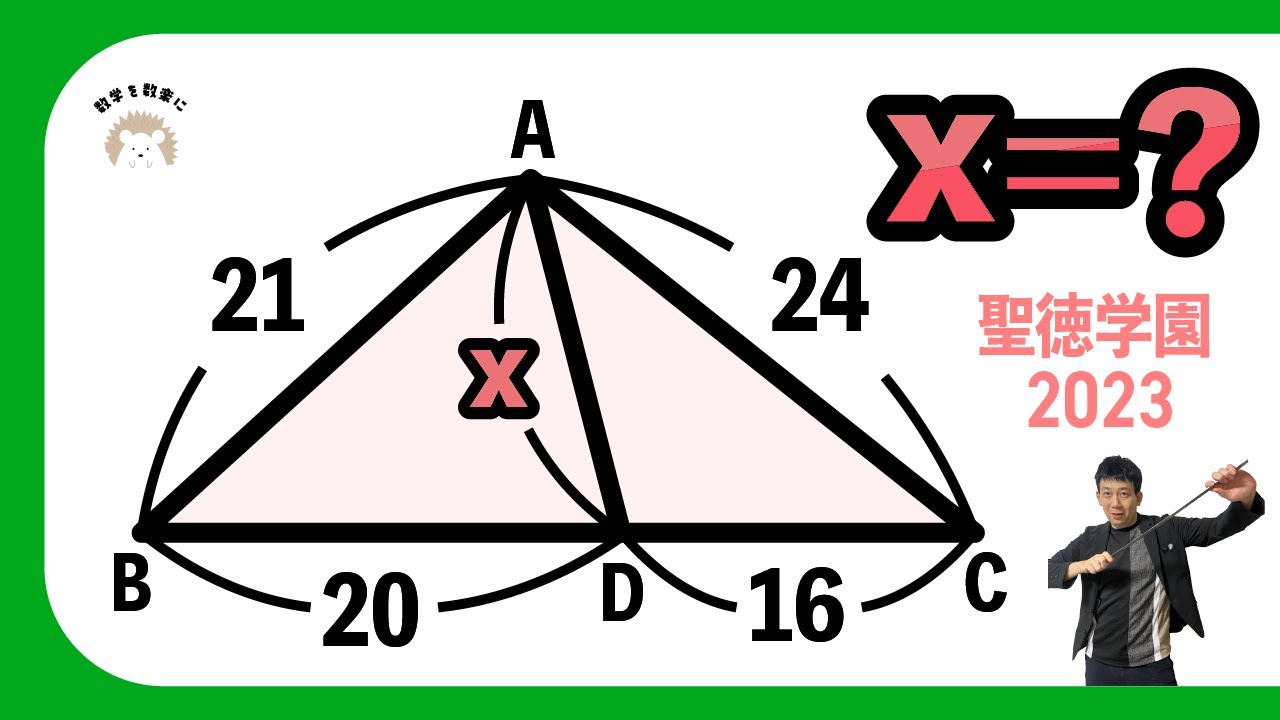
単元：
#大学入試過去問(数学)#相似な図形#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
x=?
＊図は動画内参照
聖徳学園高等学校2023
この動画を見る
x=?
＊図は動画内参照
聖徳学園高等学校2023
福田の数学〜慶應義塾大学2024年薬学部第2問〜放物線と円が接する条件と面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 原点をOとする$xy$平面上に円$x^2$+$y^2$－$12y$=0 があり、円の中心をPとする。
円周上に動点Qがあり、半直線POを始線とする動径PQの回転角を$\theta$とする。
ただし、$\theta$は$-\frac{\pi}{2}$＜$\theta$＜$\frac{\pi}{2}$を満たす実数とする。
(1)直線PQを表す方程式は、$\theta$=0 のとき$\boxed{\ \ ソ\ \ }$であり、$\theta$≠0 のとき$\boxed{\ \ タ\ \ }$である。
(2)点Qを通る放物線$y$=$ax^2$+$b$ をおく。点Qにおける放物線の接線は、点Qにおける円の接線と一致する。ただし、$a$, $b$は実数であり、$a$は$a$＞0 を満たす。
(i)$\theta$≠0 のとき$a$と$b$を$\theta$で表すと、$a$=$\boxed{\ \ チ\ \ }$, $b$=$\boxed{\ \ ツ\ \ }$ である。
(ii)$\theta$=$-\frac{\pi}{3}$ のとき、直線PQと放物線で囲まれる部分の面積は$\boxed{\ \ テ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ 原点をOとする$xy$平面上に円$x^2$+$y^2$－$12y$=0 があり、円の中心をPとする。
円周上に動点Qがあり、半直線POを始線とする動径PQの回転角を$\theta$とする。
ただし、$\theta$は$-\frac{\pi}{2}$＜$\theta$＜$\frac{\pi}{2}$を満たす実数とする。
(1)直線PQを表す方程式は、$\theta$=0 のとき$\boxed{\ \ ソ\ \ }$であり、$\theta$≠0 のとき$\boxed{\ \ タ\ \ }$である。
(2)点Qを通る放物線$y$=$ax^2$+$b$ をおく。点Qにおける放物線の接線は、点Qにおける円の接線と一致する。ただし、$a$, $b$は実数であり、$a$は$a$＞0 を満たす。
(i)$\theta$≠0 のとき$a$と$b$を$\theta$で表すと、$a$=$\boxed{\ \ チ\ \ }$, $b$=$\boxed{\ \ ツ\ \ }$ である。
(ii)$\theta$=$-\frac{\pi}{3}$ のとき、直線PQと放物線で囲まれる部分の面積は$\boxed{\ \ テ\ \ }$である。
大学入試問題#776「シグマの気持ち」 横浜国立大学(1996)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to +\infty } \displaystyle \frac{1}{n}log\{\displaystyle \frac{n}{n}・\displaystyle \frac{n+2}{n}・\displaystyle \frac{n+4}{n}・・・\displaystyle \frac{n+2(n-1)}{n}\}$
出典：1996年横浜国立大学
この動画を見る
$\displaystyle \lim_{ n \to +\infty } \displaystyle \frac{1}{n}log\{\displaystyle \frac{n}{n}・\displaystyle \frac{n+2}{n}・\displaystyle \frac{n+4}{n}・・・\displaystyle \frac{n+2(n-1)}{n}\}$
出典：1996年横浜国立大学
福田の数学〜慶應義塾大学2024年薬学部第1問(6)〜最大値と最小値と中央値の関係
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (6)偶数個の実数のデータ$x_i$(1≦$i$≦$2n$) があり、このデータの最大値を$A_{2n}$、最小値を$B_{2n}$、中央値を$C_{2n}$とし、$\displaystyle\sum_{i=1}^{2n}x_i$を$S_{2n}$とする。$A_{2n}$, $B_{2n}$, $C_{2n}$の値はわかっていおり、互いに異なる。$n$は$n$＞2を満たす整数とする。
(i)$A_8$=6、$B_8$=1、$C_8$=3、であるとき、$S_8$のとりうる値の範囲は$\boxed{\ \ ス\ \ }$である。
(ii)$S_{2n}$のとりうる値の範囲を$A_{2n}$, $B_{2n}$, $C_{2n}$を用いて表すと、$\boxed{\ \ セ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (6)偶数個の実数のデータ$x_i$(1≦$i$≦$2n$) があり、このデータの最大値を$A_{2n}$、最小値を$B_{2n}$、中央値を$C_{2n}$とし、$\displaystyle\sum_{i=1}^{2n}x_i$を$S_{2n}$とする。$A_{2n}$, $B_{2n}$, $C_{2n}$の値はわかっていおり、互いに異なる。$n$は$n$＞2を満たす整数とする。
(i)$A_8$=6、$B_8$=1、$C_8$=3、であるとき、$S_8$のとりうる値の範囲は$\boxed{\ \ ス\ \ }$である。
(ii)$S_{2n}$のとりうる値の範囲を$A_{2n}$, $B_{2n}$, $C_{2n}$を用いて表すと、$\boxed{\ \ セ\ \ }$である。
#広島市立大学(2016) #定積分 #Shorts
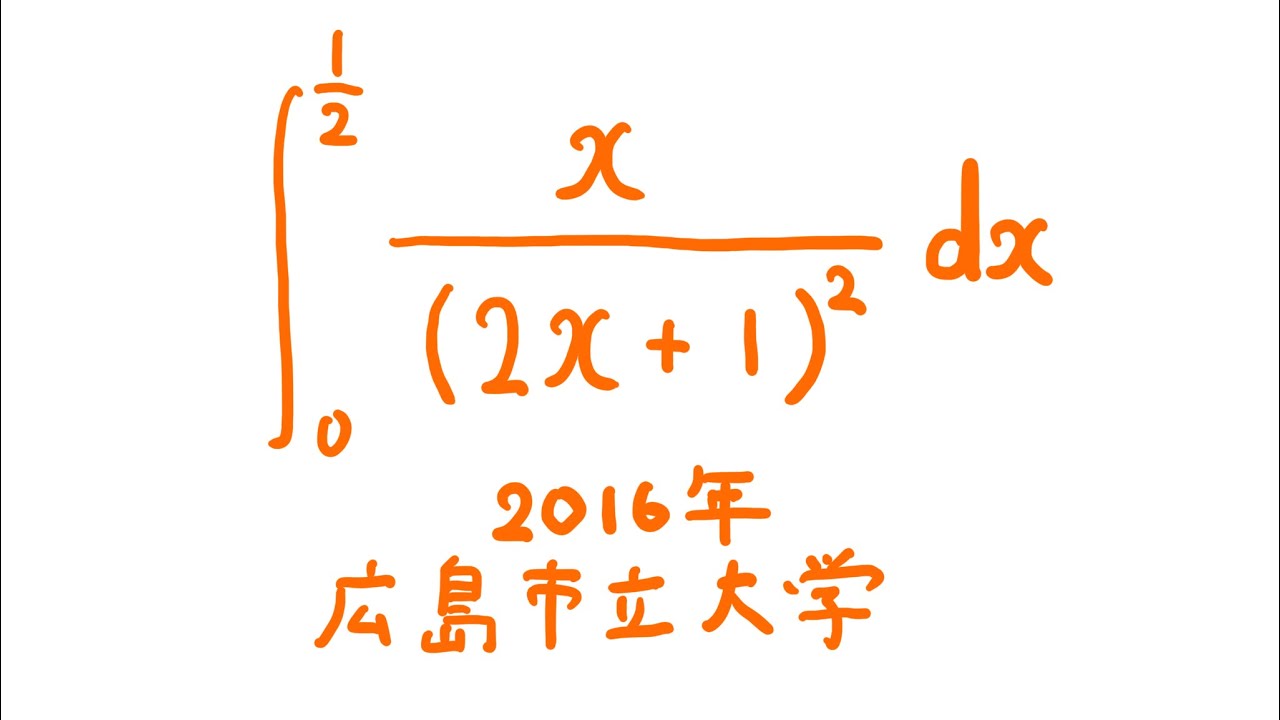
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x}{(2x+1)^2} dx$
出典：2016年広島市立大学
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x}{(2x+1)^2} dx$
出典：2016年広島市立大学
【高校数学】群馬大学医学部の積分の問題をその場で解説しながら解いてみた！毎日積分96日目~47都道府県制覇への道~【㊴群馬】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【群馬大学(医) 2023】
$xy$平面上において、不等式$(ye^x)^2≦(sin2x)^2, 0≦x≦π$の表す領域を$D$とし、領域$D$と直線$x=a$の共通部分の線分の長さを$l(a)$とする。以下の問に答えよ。
(1) $l(a)$が$a=a_0$で最大となるとき、$tana_0$の値を求めよ。
(2)領域$D$の面積を求めよ。
この動画を見る
【群馬大学(医) 2023】
$xy$平面上において、不等式$(ye^x)^2≦(sin2x)^2, 0≦x≦π$の表す領域を$D$とし、領域$D$と直線$x=a$の共通部分の線分の長さを$l(a)$とする。以下の問に答えよ。
(1) $l(a)$が$a=a_0$で最大となるとき、$tana_0$の値を求めよ。
(2)領域$D$の面積を求めよ。
二次関数と変域 2024明大中野
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$y=\frac{1}{3}x^2$について、xの変域が$a-6 \leqq x \leqq a$のとき、yの変域は$0 \leqq y \leqq 9$となる。
aの値をすべて求めよ。
2024明治大学付属中野高等学校
この動画を見る
$y=\frac{1}{3}x^2$について、xの変域が$a-6 \leqq x \leqq a$のとき、yの変域は$0 \leqq y \leqq 9$となる。
aの値をすべて求めよ。
2024明治大学付属中野高等学校
大学入試問題#775「ほぼ、詰んでる」 横浜国立大学(1998) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$
出典：1998年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$
出典：1998年横浜国立大学 入試問題
福田の数学〜慶應義塾大学2024年薬学部第1問(5)〜整数解と素数の性質
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (5)自然数$a$,$b$と素数$p$は等式
$a^4$－$4a^2b$+$4b^3$－$b^4$=$p^2$
を満たす。このとき、数の組($a$,$b$,$p$)を全て求めると($a$,$b$,$p$)$\boxed{\ \ シ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (5)自然数$a$,$b$と素数$p$は等式
$a^4$－$4a^2b$+$4b^3$－$b^4$=$p^2$
を満たす。このとき、数の組($a$,$b$,$p$)を全て求めると($a$,$b$,$p$)$\boxed{\ \ シ\ \ }$である。
【高校数学】筑波大学の積分の問題をその場で解説しながら解いてみた！毎日積分95日目~47都道府県制覇への道~【㊳茨城】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【筑波大学 2023】
$a,b$を実数とし、$f(x)=x+asinx, g(x)=bcosx$とする。
(1) 定積分$\displaystyle \int_{-π}^{π}f(x)g(x)dx$を求めよ。
(2)不等式
$\displaystyle \int_{-π}^{π}\{f(x)+g(x)\}^2dx≧\int_{-π}^{π}\{f(x)\}^2dx$
が成り立つことを示せ。
(3) 曲線$y=|f(x)+g(x)|$, 2直線$x=-π, x=π,$および$x$軸で囲まれた図形を$x$軸の周りに1回転させてできる回転体の体積を$V$とする。このとき不等式
$\displaystyle V≧\frac{2}{3}π^2(π^2-6)$
が成り立つことを示せ。さらに、等号が成立するときの$a,b$を求めよ。
この動画を見る
【筑波大学 2023】
$a,b$を実数とし、$f(x)=x+asinx, g(x)=bcosx$とする。
(1) 定積分$\displaystyle \int_{-π}^{π}f(x)g(x)dx$を求めよ。
(2)不等式
$\displaystyle \int_{-π}^{π}\{f(x)+g(x)\}^2dx≧\int_{-π}^{π}\{f(x)\}^2dx$
が成り立つことを示せ。
(3) 曲線$y=|f(x)+g(x)|$, 2直線$x=-π, x=π,$および$x$軸で囲まれた図形を$x$軸の周りに1回転させてできる回転体の体積を$V$とする。このとき不等式
$\displaystyle V≧\frac{2}{3}π^2(π^2-6)$
が成り立つことを示せ。さらに、等号が成立するときの$a,b$を求めよ。
約数の個数とその総和 2024明大中野
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
・正の約数を3個だけ持つ
・その約数の総和は871
この自然数を求めよ。
2024明治大学付属中野高等学校
この動画を見る
・正の約数を3個だけ持つ
・その約数の総和は871
この自然数を求めよ。
2024明治大学付属中野高等学校
大学入試問題#774「基本的な良問」 横浜国立大学(1998) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e-1} \displaystyle \frac{log(log(x+1))}{x+1} dx$
出典：1998年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e-1} \displaystyle \frac{log(log(x+1))}{x+1} dx$
出典：1998年横浜国立大学 入試問題
福田の数学〜慶應義塾大学2024年薬学部第1問(4)〜空間図形の計量
単元：
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (4)Oを原点とする$xyz$空間に点A(0,0,$\sqrt 6$)があり、$y$軸上の点B, C($t$,$\frac{t}{\tan\theta}$,0)を∠OBA=30°,∠BAC=45°,∠ACB=60° を満たすようにおく。ただし$t$は$t$＞0 を満たす実数の定数、$\theta$は0°＜$\theta$＜90°を満たす実数の定数とする。
(i)$|\overrightarrow{BC}|$=$\boxed{\ \ ケ\ \ }$である。
(ii)$|\overrightarrow{OC}|^2$=$\boxed{\ \ コ\ \ }$である。
(iii)$\theta$は$\tan^2\theta$の値が$\boxed{\ \ サ\ \ }$となる実数である。
この動画を見る
$\Large\boxed{1}$ (4)Oを原点とする$xyz$空間に点A(0,0,$\sqrt 6$)があり、$y$軸上の点B, C($t$,$\frac{t}{\tan\theta}$,0)を∠OBA=30°,∠BAC=45°,∠ACB=60° を満たすようにおく。ただし$t$は$t$＞0 を満たす実数の定数、$\theta$は0°＜$\theta$＜90°を満たす実数の定数とする。
(i)$|\overrightarrow{BC}|$=$\boxed{\ \ ケ\ \ }$である。
(ii)$|\overrightarrow{OC}|^2$=$\boxed{\ \ コ\ \ }$である。
(iii)$\theta$は$\tan^2\theta$の値が$\boxed{\ \ サ\ \ }$となる実数である。
#広島市立大学(2016) #定積分 #Shorts
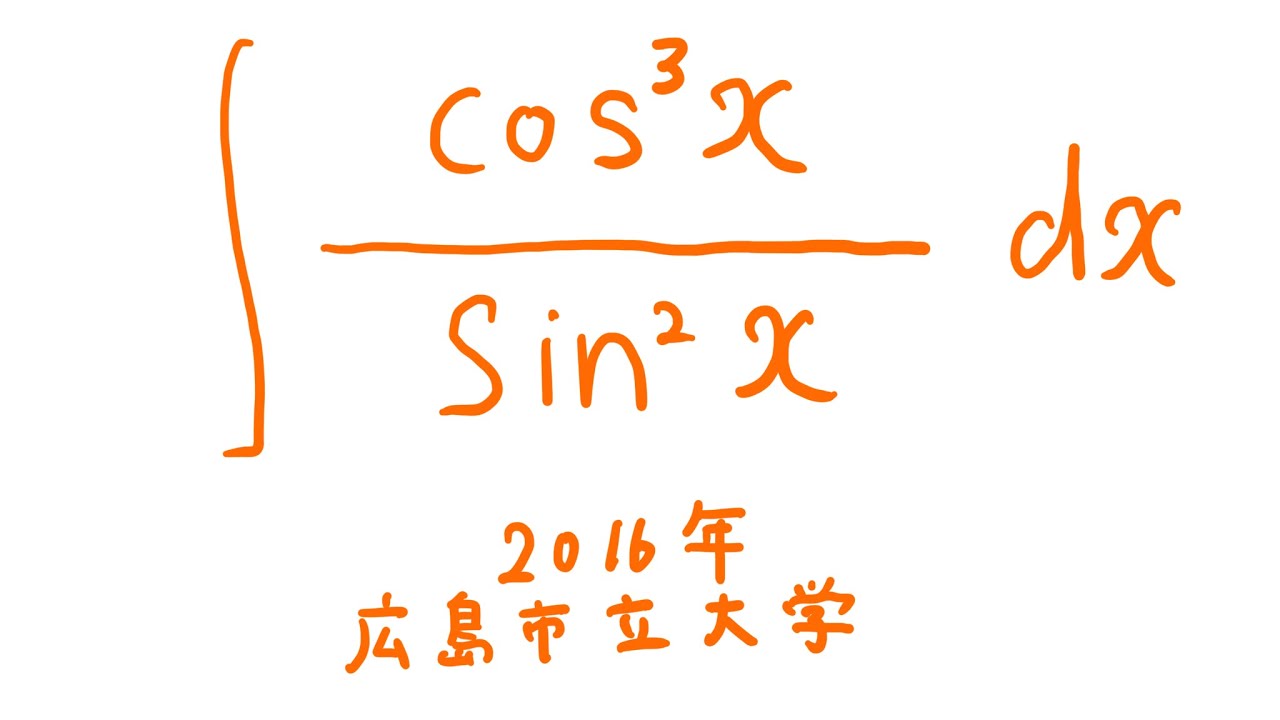
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典：2016年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典：2016年広島市立大学
【高校数学】千葉大学の積分の問題をその場で解説しながら解いてみた！毎日積分94日目~47都道府県制覇への道~【㊲千葉】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【千葉大学 2023】
等式$\displaystyle f(x)=x^2+\int_{-1}^{2}(xf(t)-t)dt$を満たす関数$f(x)$を求めよ。
この動画を見る
【千葉大学 2023】
等式$\displaystyle f(x)=x^2+\int_{-1}^{2}(xf(t)-t)dt$を満たす関数$f(x)$を求めよ。
大学入試問題#773「綺麗な良問」 青山学院大学(2019) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
素数$p.q$および自然数$n$に対し
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{pq}=\displaystyle \frac{1}{n}$
が成り立つような$(p,q,n)$の組をすべて求めよ
出典：2019年青山学院大学
この動画を見る
素数$p.q$および自然数$n$に対し
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{pq}=\displaystyle \frac{1}{n}$
が成り立つような$(p,q,n)$の組をすべて求めよ
出典：2019年青山学院大学
2次方程式 3通りで解説！！ 2024日比谷高校
単元：
#数Ⅰ#大学入試過去問(数学)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$(x-1)^2-4(x-2)^2=0$
2024日比谷高等学校
この動画を見る
方程式を解け
$(x-1)^2-4(x-2)^2=0$
2024日比谷高等学校
福田の数学〜慶應義塾大学2024年薬学部第1問(3)〜領域における最大最小
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (3)$xy$平面上に連立不等式$x$+$y$≦4, $5x$－$7y$≧－40, $x$－$3y$≦－8 の表す領域Dがある。点P($x$,$y$)がD内を動くとき、$x^2$+$y^2$の最小値は$\boxed{\ \ キ\ \ }$であり、最大値は$\boxed{\ \ ク\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (3)$xy$平面上に連立不等式$x$+$y$≦4, $5x$－$7y$≧－40, $x$－$3y$≦－8 の表す領域Dがある。点P($x$,$y$)がD内を動くとき、$x^2$+$y^2$の最小値は$\boxed{\ \ キ\ \ }$であり、最大値は$\boxed{\ \ ク\ \ }$である。
2024山口大 １の10乗根のナイスな問題
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形と計量#三角比への応用（正弦・余弦・面積）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$2Z^4+(1-\sqrt{ 5 })Z^2+2=0$であるとき
(1)$Z^{10}=1$であることを示せ
(2)$\cos \displaystyle \frac{\pi}{5} \cos \displaystyle \frac{2\pi}{5}=\displaystyle \frac{1}{4}$を示せ
出典：2024年山口大学数学 過去問
この動画を見る
$2Z^4+(1-\sqrt{ 5 })Z^2+2=0$であるとき
(1)$Z^{10}=1$であることを示せ
(2)$\cos \displaystyle \frac{\pi}{5} \cos \displaystyle \frac{2\pi}{5}=\displaystyle \frac{1}{4}$を示せ
出典：2024年山口大学数学 過去問
【高校数学】埼玉大学の積分の問題をその場で解説しながら解いてみた！毎日積分93日目~47都道府県制覇への道~【㊱埼玉】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【埼玉大学 2017】
関数$f(x)$は微分可能で
$\displaystyle f(x)=x^2e^{-x}+\int_0^xe^{t-x}f(t)dt$
を満たすものとする。次の問いに答えよ。
(1) $f(0),f'(0)$を求めよ。
(2) $f'(x)$を求めよ。
(3) $f(x)$を求めよ。
この動画を見る
【埼玉大学 2017】
関数$f(x)$は微分可能で
$\displaystyle f(x)=x^2e^{-x}+\int_0^xe^{t-x}f(t)dt$
を満たすものとする。次の問いに答えよ。
(1) $f(0),f'(0)$を求めよ。
(2) $f'(x)$を求めよ。
(3) $f(x)$を求めよ。
大学入試の連立方程式 東北学院大
単元：
#連立方程式#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=8 \\
z(x+y)=9
\end{array}
\right.
\end{eqnarray}
東北学院大学
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=8 \\
z(x+y)=9
\end{array}
\right.
\end{eqnarray}
東北学院大学
大学入試問題#772「初手は好みがでそう」 広島市立大学(2012) #不定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{log\ x}{\sqrt[ 3 ]{ x }} dx$
出典：2012年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{log\ x}{\sqrt[ 3 ]{ x }} dx$
出典：2012年広島市立大学 入試問題
【高校数学】東京大学2024年の積分の問題をその場で解説しながら解いてみた！毎日積分92日目~47都道府県制覇への道~【㉟東京】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【東京大学 2024】
座標空間内に3点A(1,0,0),B(0,1,0),C(0,0,1)をとり、D を線分ACの中点とする。三角形ABDの周および内部をx軸のまわりに1回転させて得られる立体の体積を求めよ。
この動画を見る
【東京大学 2024】
座標空間内に3点A(1,0,0),B(0,1,0),C(0,0,1)をとり、D を線分ACの中点とする。三角形ABDの周および内部をx軸のまわりに1回転させて得られる立体の体積を求めよ。
大学入試問題#771「たぶん良問！」 島根大学後期(2023) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1} dx$
出典：2023年島根大学後期 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1} dx$
出典：2023年島根大学後期 入試問題
【高校数学】横浜国立大学2023年の積分の問題をその場で解説しながら解いてみた！毎日積分91日目~47都道府県制覇への道~【㉞神奈川】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【横浜国立大学(後) 2023】
$\displaystyle \int_{log\frac{π}{4}}^{log\frac{π}{2}}\frac{e^{2x}}{\{sin(e^x)\}^2}dx$
この動画を見る
【横浜国立大学(後) 2023】
$\displaystyle \int_{log\frac{π}{4}}^{log\frac{π}{2}}\frac{e^{2x}}{\{sin(e^x)\}^2}dx$
大学入試の因数分解 神戸女子大
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$a^4+a^2b^2+b^4$
神戸女子大学
この動画を見る
因数分解せよ
$a^4+a^2b^2+b^4$
神戸女子大学
大学入試問題#770「減点注意！」 千葉大学(2003) #微積の応用
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典：2003年千葉大学 入試問題
この動画を見る
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典：2003年千葉大学 入試問題
【高校数学】新潟大学2023年の積分の問題をその場で解説しながら解いてみた！毎日積分90日目~47都道府県制覇への道~【㉝新潟】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【新潟大学 2023】
$a,b$を正の数とし、座標平面上の曲線
$C_1:y=e^{ax}, C_2:y=\sqrt{2x-b}$
を考える。次の問いに答えよ。
(1)関数$y=e^{ax}$,と関数$y=\sqrt{2x-b}$の導関数を求めよ。
(2)曲線$C_1$と曲線$C_2$が1点$P$を共有し、その点において共通の接線をもつとする。この時,$b$と点$P$の座標を$a$を用いて表せ。
(3) (2)において、曲線$C_1$,曲線$C_2$,$x$軸,$y$軸で囲まれる図形の面積を$a$を用いて表せ。
この動画を見る
【新潟大学 2023】
$a,b$を正の数とし、座標平面上の曲線
$C_1:y=e^{ax}, C_2:y=\sqrt{2x-b}$
を考える。次の問いに答えよ。
(1)関数$y=e^{ax}$,と関数$y=\sqrt{2x-b}$の導関数を求めよ。
(2)曲線$C_1$と曲線$C_2$が1点$P$を共有し、その点において共通の接線をもつとする。この時,$b$と点$P$の座標を$a$を用いて表せ。
(3) (2)において、曲線$C_1$,曲線$C_2$,$x$軸,$y$軸で囲まれる図形の面積を$a$を用いて表せ。
大学入試問題#769「受験生は抑えたい良問」 日本医科大学(2013) #微積の応用
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{3}{2} \leq \displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{2^2}+・・・+\displaystyle \frac{1}{n^2}) \leq 2$を示せ。
出典：2013年日本医科大学 入試問題
この動画を見る
$\displaystyle \frac{3}{2} \leq \displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{2^2}+・・・+\displaystyle \frac{1}{n^2}) \leq 2$を示せ。
出典：2013年日本医科大学 入試問題
福田の数学〜東京工業大学2024年理系第4問〜表の出る確率が異なるコインを投げたときの表が奇数枚出る確率と極限
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1－$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1－$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。