 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
#宮崎大学 2020年 #定積分 #Shorts
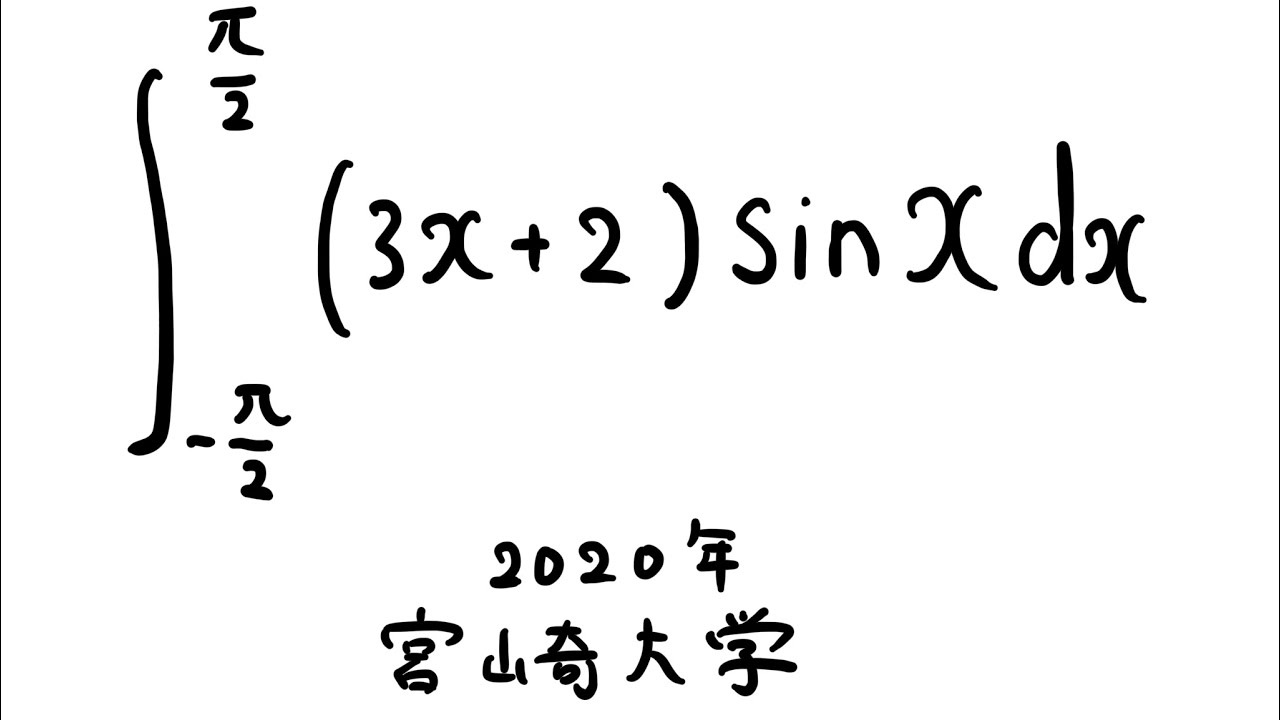
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (3x+2)\sin\ x\ dx$
出典:2020年宮崎大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (3x+2)\sin\ x\ dx$
出典:2020年宮崎大学
【高校数学】福井大学2023年の積分の問題をその場で解説しながら解いてみた!毎日積分83日目~47都道府県制覇への道~【㉖福井】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#福井大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【福井大学 2023】
$f(t)=2e^t-e^{2t}, g(t)=te^t$とし、$f(t)$が極大となる$t$の値を$α$、$f(t)=0$となる$t$の値を$β$とする。$xy$平面上の曲線$C$を$x=f(t), y=g(t) (α≦t≦β)$で与える。以下の問いに答えよ。
(1) $α$と$β$の値を求めよ。
(2) $α<t<β$の範囲で、$\frac{dy}{dx}$を$t$の関数として表せ。
(3) 曲線$C$と$x$軸および$y$軸で囲まれた図形の面積を求めよ。
この動画を見る
【福井大学 2023】
$f(t)=2e^t-e^{2t}, g(t)=te^t$とし、$f(t)$が極大となる$t$の値を$α$、$f(t)=0$となる$t$の値を$β$とする。$xy$平面上の曲線$C$を$x=f(t), y=g(t) (α≦t≦β)$で与える。以下の問いに答えよ。
(1) $α$と$β$の値を求めよ。
(2) $α<t<β$の範囲で、$\frac{dy}{dx}$を$t$の関数として表せ。
(3) 曲線$C$と$x$軸および$y$軸で囲まれた図形の面積を求めよ。
意外と間違える!?二次方程式 2024京都府

単元:
#数Ⅰ#大学入試過去問(数学)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$8x^2=22x$
2024京都府
この動画を見る
方程式を解け
$8x^2=22x$
2024京都府
大学入試問題#762「再生回数は、期待できない」 東京理科大学工学部(2003) #曲線の長さ

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
曲線$y=(2x+1)\sqrt{ 2x+1 }$の区間$0 \leq x \leq \displaystyle \frac{1}{3}$にある部分の長さを求めよ。
出典:2003年東京理科大学工学部 入試問題
この動画を見る
曲線$y=(2x+1)\sqrt{ 2x+1 }$の区間$0 \leq x \leq \displaystyle \frac{1}{3}$にある部分の長さを求めよ。
出典:2003年東京理科大学工学部 入試問題
福田の数学〜京都大学2024年文系第1問〜四面体の体積
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
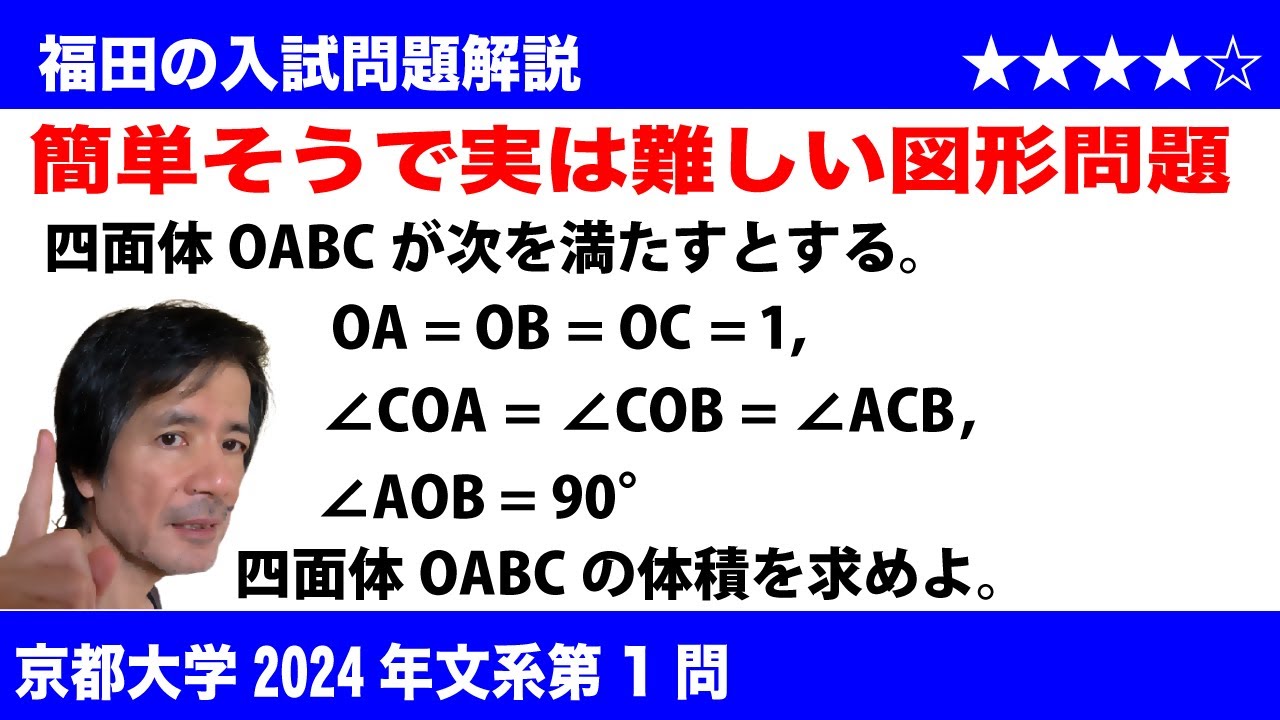
$\Large\boxed{1}$ 四面体OABCが次を満たすとする。
OA=OB=OC=1, ∠COA=∠COB=∠ACB, ∠AOB=90°
このとき、四面体OABCの体積を求めよ。
この動画を見る
$\Large\boxed{1}$ 四面体OABCが次を満たすとする。
OA=OB=OC=1, ∠COA=∠COB=∠ACB, ∠AOB=90°
このとき、四面体OABCの体積を求めよ。
2024早稲田(教育)循環小数を2進法で表せ

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{4}{9}$を2進法の循環小数で表せ
出典:2024年早稲田大学教育学部過去問
この動画を見る
$\displaystyle \frac{4}{9}$を2進法の循環小数で表せ
出典:2024年早稲田大学教育学部過去問
#宮崎大学 2022年 #定積分 #Shorts
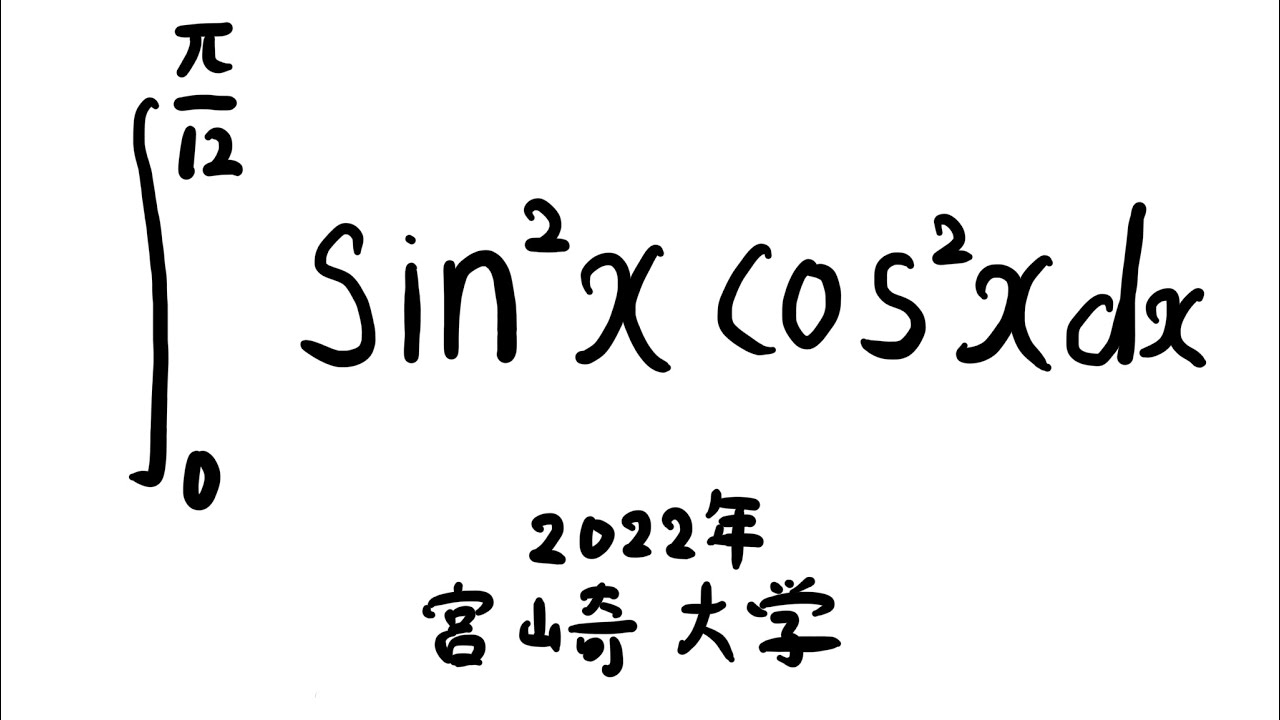
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{12}} \sin^2x\ \cos^2x\ dx$
出典:2022年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{12}} \sin^2x\ \cos^2x\ dx$
出典:2022年宮崎大学
【高校数学】名古屋大学2024年の手強い積分の問題をその場で解説しながら解いてみた!毎日積分82日目~47都道府県制覇への道~【㉕愛知】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【名古屋大学 2024】
袋の中にいくつかの赤玉と白玉が入っている。すべての玉に対する赤玉の割合を$p(0≦p≦1)$とする。袋から無作為に玉を一つ取り出して袋に戻す試行を行う。試行を$n$回行うとき、赤玉を$k$回以上取り出す確率を$f(k)$をおく。
(1) $n≧2$に対して、$f(1), f(2)$を求めよ。
(2) $k=1,2, ・・・・・・,n$に対して、等式
$\displaystyle f(k)=\frac{n!}{(k-1)!(n-k)!}\int_0^px^{k-1}(1-x)^{n-k}dx$
を示せ。
(3) 自然数$k$に対して、定積分
$\displaystyle I=\int_0^{\frac{1}{2}}x^k(1-x)^k dx$
を求めよ。
この動画を見る
【名古屋大学 2024】
袋の中にいくつかの赤玉と白玉が入っている。すべての玉に対する赤玉の割合を$p(0≦p≦1)$とする。袋から無作為に玉を一つ取り出して袋に戻す試行を行う。試行を$n$回行うとき、赤玉を$k$回以上取り出す確率を$f(k)$をおく。
(1) $n≧2$に対して、$f(1), f(2)$を求めよ。
(2) $k=1,2, ・・・・・・,n$に対して、等式
$\displaystyle f(k)=\frac{n!}{(k-1)!(n-k)!}\int_0^px^{k-1}(1-x)^{n-k}dx$
を示せ。
(3) 自然数$k$に対して、定積分
$\displaystyle I=\int_0^{\frac{1}{2}}x^k(1-x)^k dx$
を求めよ。
大学入試問題#761「微積の入試勉強は、まずこれから!」 東京理科大学理学部(2002) #微積

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
関数$F(x)$を
$F(x)=\displaystyle \int_{0}^{x} (\sin\ t+\cos\ t)^2 dt$と定める。
$F(x),\displaystyle \lim_{ x \to \infty } \displaystyle \frac{F(x)}{x},\displaystyle \lim_{ x \to 0 } \displaystyle \frac{F(x)}{x}$を求めよ。
出典:2002年東京理科大学理学部 入試問題
この動画を見る
関数$F(x)$を
$F(x)=\displaystyle \int_{0}^{x} (\sin\ t+\cos\ t)^2 dt$と定める。
$F(x),\displaystyle \lim_{ x \to \infty } \displaystyle \frac{F(x)}{x},\displaystyle \lim_{ x \to 0 } \displaystyle \frac{F(x)}{x}$を求めよ。
出典:2002年東京理科大学理学部 入試問題
福田の数学〜京都大学2024年理系第6問〜桁数がn桁の数列の中に含まれる最高位1の項の割合

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 自然数$k$に対して、$a_k$=$2^{\sqrt k}$とする。$n$を自然数とし、$a_k$の整数部分が$n$桁であるような$k$の個数を$N_n$とする。また、$a_k$の整数部分が$n$桁であり、その最高位の数字が1であるような$k$の個数を$L_n$とする。次を求めよ。
$\displaystyle\lim_{n \to \infty}\frac{L_n}{N_n}$
ただし、例えば実数2345.678 の整数部分2345は4桁で、最高位の数字は2である。
この動画を見る
$\Large\boxed{6}$ 自然数$k$に対して、$a_k$=$2^{\sqrt k}$とする。$n$を自然数とし、$a_k$の整数部分が$n$桁であるような$k$の個数を$N_n$とする。また、$a_k$の整数部分が$n$桁であり、その最高位の数字が1であるような$k$の個数を$L_n$とする。次を求めよ。
$\displaystyle\lim_{n \to \infty}\frac{L_n}{N_n}$
ただし、例えば実数2345.678 の整数部分2345は4桁で、最高位の数字は2である。
【高校数学】ワイエルシュトラス置換って何!?毎日積分81日目~47都道府県制覇への道~【㉔三重】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【三重大学 2009】
$\displaystyle \int_\frac{π}{3}^{\frac{π}{2}}\frac{1}{1+sinθ-cosθ}dθ$
この動画を見る
【三重大学 2009】
$\displaystyle \int_\frac{π}{3}^{\frac{π}{2}}\frac{1}{1+sinθ-cosθ}dθ$
大学入試問題#760「ほぼ一直線」 東京理科大学(2003) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
定積分
$I=\displaystyle \int_{1}^{4} t^2\sin(\displaystyle \frac{\pi}{4}t\sqrt{ t })\ dt$を求めよ。
出典:2003年東京理科大学 入試問題
この動画を見る
定積分
$I=\displaystyle \int_{1}^{4} t^2\sin(\displaystyle \frac{\pi}{4}t\sqrt{ t })\ dt$を求めよ。
出典:2003年東京理科大学 入試問題
福田の数学〜京都大学2024年理系第5問〜指数関数で囲まれた図形の面積と極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $a$は$a$≧1を満たす定数とする。座標平面上で、次の4つの不等式が表す領域を$D_a$とする。
$x$≧0, $\frac{e^x-e^{-x}}{2}$≦$y$, $y$≦$\frac{e^x+e^{-x}}{2}$, $y$≦$a$
次の問いに答えよ。
(1)$D_a$の面積$S_a$を求めよ。
(2)$\displaystyle\lim_{a \to \infty}S_a$ を求めよ。
この動画を見る
$\Large\boxed{5}$ $a$は$a$≧1を満たす定数とする。座標平面上で、次の4つの不等式が表す領域を$D_a$とする。
$x$≧0, $\frac{e^x-e^{-x}}{2}$≦$y$, $y$≦$\frac{e^x+e^{-x}}{2}$, $y$≦$a$
次の問いに答えよ。
(1)$D_a$の面積$S_a$を求めよ。
(2)$\displaystyle\lim_{a \to \infty}S_a$ を求めよ。
【高校数学】滋賀医科大学2023年の積分の問題をその場で解説しながら解いてみた!毎日積分80日目~47都道府県制覇への道~【㉓滋賀】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#滋賀医科大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【滋賀医科大学 2023】
実数全体を定義域とする微分可能な関数$f(x)$は、常に$f(x)>0$であり、等式
$\displaystyle f(x)=1+\int_0^x e^t(1+t)f(t)dt$
を満たしている。
(1) $f(0)$を求めよ。
(2) $logf(x)$の導関数$(logf(x))’$を求めよ。
(3) 関数$f(x)$を求めよ。
(4) 方程式$f(x)=\frac{1}{\sqrt{2}}$を解け。
この動画を見る
【滋賀医科大学 2023】
実数全体を定義域とする微分可能な関数$f(x)$は、常に$f(x)>0$であり、等式
$\displaystyle f(x)=1+\int_0^x e^t(1+t)f(t)dt$
を満たしている。
(1) $f(0)$を求めよ。
(2) $logf(x)$の導関数$(logf(x))’$を求めよ。
(3) 関数$f(x)$を求めよ。
(4) 方程式$f(x)=\frac{1}{\sqrt{2}}$を解け。
大学入試の因数分解 2通りで解説 近畿大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^3-3x^2-6x+8$
近畿大学
この動画を見る
因数分解せよ
$x^3-3x^2-6x+8$
近畿大学
大学入試問題#759「サムネみすった」 東京理科大学(2002) #定積分
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
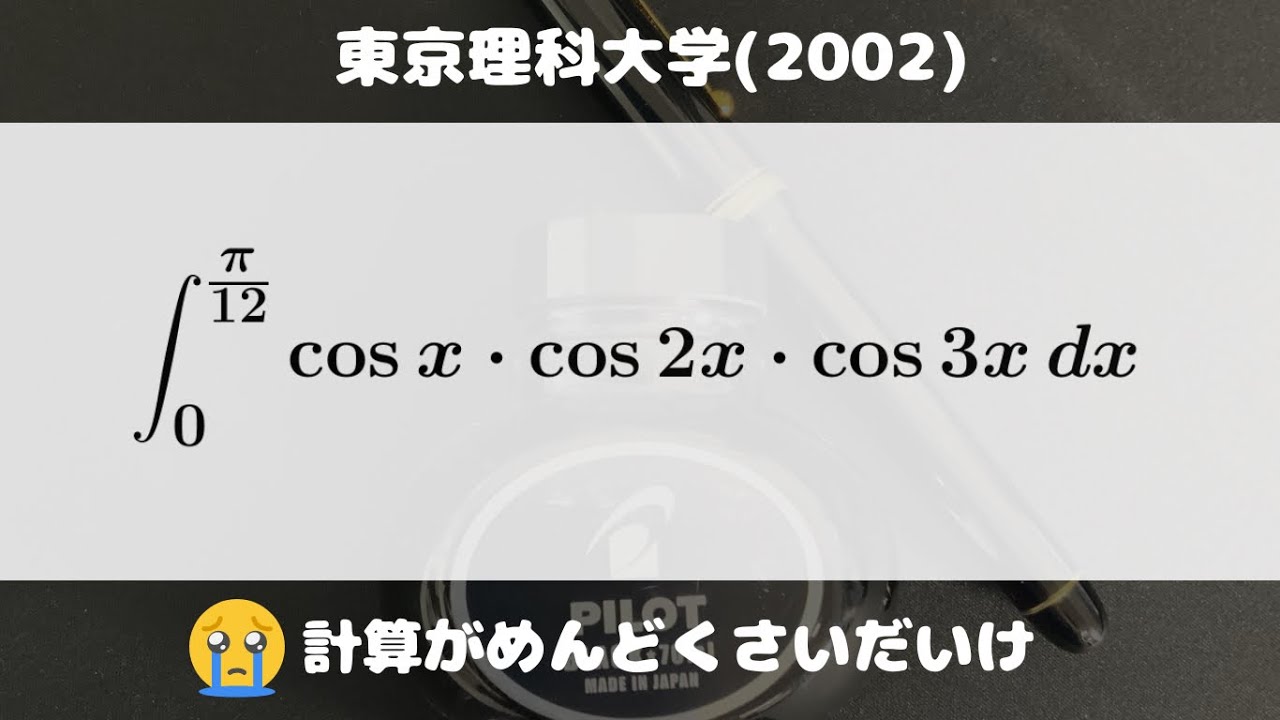
$\displaystyle \int_{0}^{\frac{\pi}{12}} \cos\ x・\cos\ 2x・\cos\ 3x\ dx$
出典:2002年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{12}} \cos\ x・\cos\ 2x・\cos\ 3x\ dx$
出典:2002年東京理科大学 入試問題
福田の数学〜京都大学2024年理系第4問〜その項が偶数であるかないかで定義が変わる漸化式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 与えられた自然数$a_0$に対して、自然数からなる数列$a_0$,$a_1$,$a_2$, ... を次のように定める。
$a_{n+1}$=$\left\{\begin{array}{1}
\displaystyle\frac{a_n}{2} (a_nが偶数のとき)\\
\displaystyle\frac{3a_n+1}{2} (a_nが奇数のとき)\\
\end{array}\right.$
次の問いに答えよ。
(1)$a_0$,$a_1$,$a_2$,$a_3$がすべて奇数であるような最小の自然数$a_0$を求めよ。
(2)$a_0$,$a_1$,...,$a_{10}$がすべて奇数であるような最小の自然数$a_0$を求めよ。
この動画を見る
$\Large\boxed{4}$ 与えられた自然数$a_0$に対して、自然数からなる数列$a_0$,$a_1$,$a_2$, ... を次のように定める。
$a_{n+1}$=$\left\{\begin{array}{1}
\displaystyle\frac{a_n}{2} (a_nが偶数のとき)\\
\displaystyle\frac{3a_n+1}{2} (a_nが奇数のとき)\\
\end{array}\right.$
次の問いに答えよ。
(1)$a_0$,$a_1$,$a_2$,$a_3$がすべて奇数であるような最小の自然数$a_0$を求めよ。
(2)$a_0$,$a_1$,...,$a_{10}$がすべて奇数であるような最小の自然数$a_0$を求めよ。
#広島市立大学 2010年 #不定積分 #Shorts
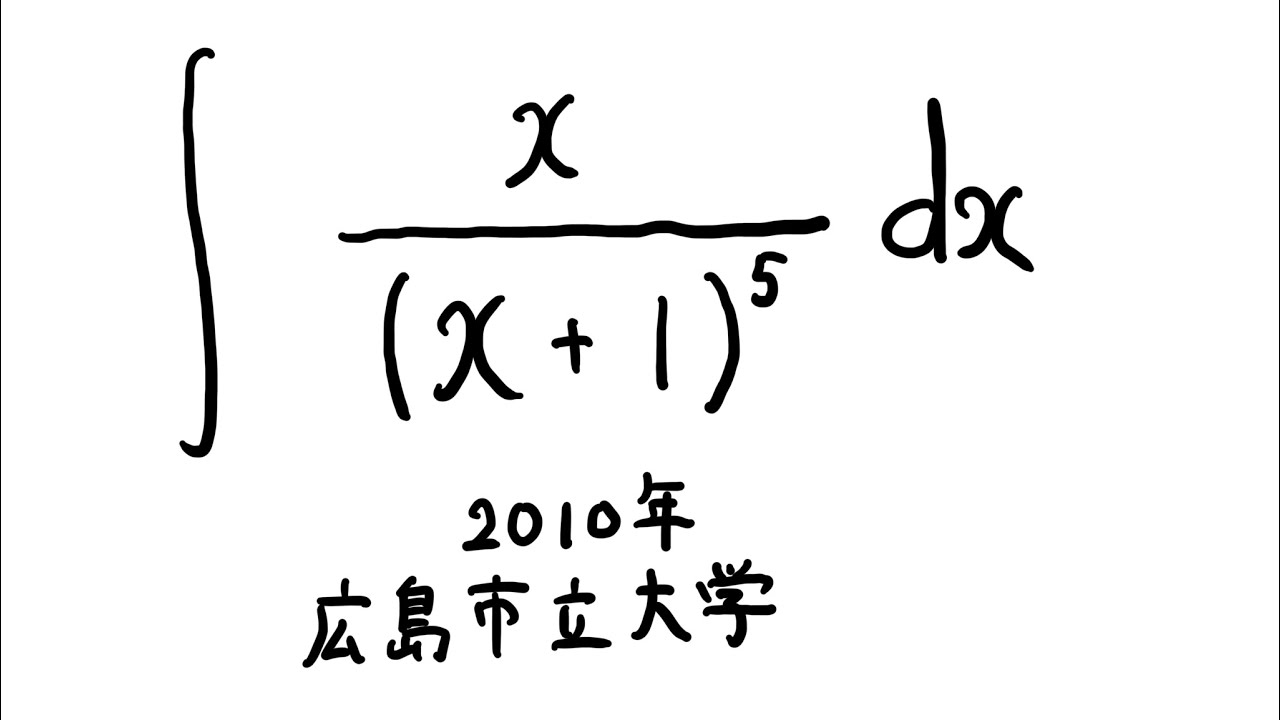
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{(x+1)^5} dx$
出典:2010年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{(x+1)^5} dx$
出典:2010年広島市立大学
【高校数学】京都大学2024年の積分の問題をその場で解説しながら解いてみた!毎日積分79日目~47都道府県制覇への道~【㉒京都】【毎日17時投稿】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【京都大学 2024】
$a$は$a≧1$を満たす定数とする。座標平面上で、次の4つの不等式が表す領域を$D_a$ とする。
$\displaystyle x≧0, \frac{e^x-e^{-x}}{2}≦y, y≦ \frac{e^x+e^{-x}}{2}, y≦a$
次の問いに答えよ。
(1) $D_a$の面積$S_a$を求めよ。
(2) $\displaystyle \lim_{a\to \infty}S_a$を求めよ。
この動画を見る
【京都大学 2024】
$a$は$a≧1$を満たす定数とする。座標平面上で、次の4つの不等式が表す領域を$D_a$ とする。
$\displaystyle x≧0, \frac{e^x-e^{-x}}{2}≦y, y≦ \frac{e^x+e^{-x}}{2}, y≦a$
次の問いに答えよ。
(1) $D_a$の面積$S_a$を求めよ。
(2) $\displaystyle \lim_{a\to \infty}S_a$を求めよ。
#広島市立大学 2010年 #不定積分 #Shorts
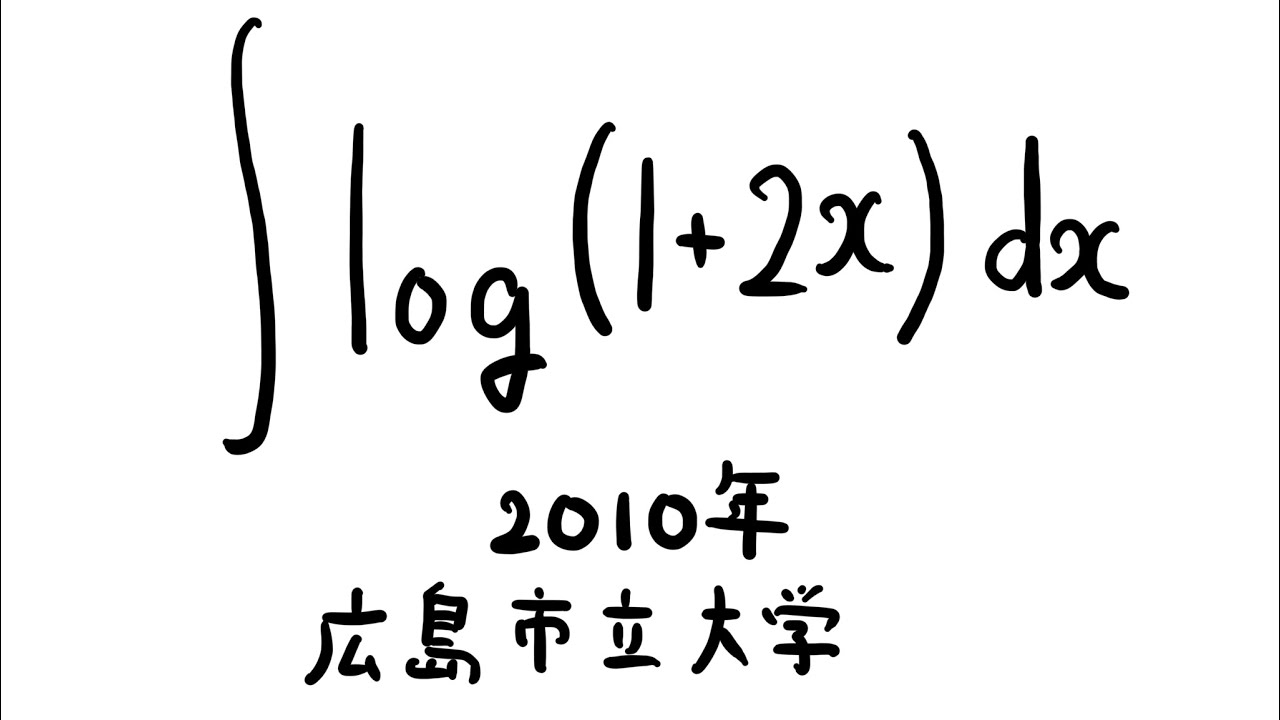
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+2x) dx$
出典:2010年広島市立大学
この動画を見る
$\displaystyle \int log(1+2x) dx$
出典:2010年広島市立大学
大学入試問題#758 「ミスりようがない。」 東京理科大学理学部(2002) #方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
方程式$(x+2)(x+3)(x-4)(x-5)=44$を解け。
出典:2002年東京理科大学理学部 入試問題
この動画を見る
方程式$(x+2)(x+3)(x-4)(x-5)=44$を解け。
出典:2002年東京理科大学理学部 入試問題
福田の数学〜京都大学2024年理系第3問〜2直線がねじれの位置になるための必要十分条件

単元:
#計算と数の性質#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標空間の4点O,A,B,Cは同一平面上にないとする。線分OAの中点をP、線分ABの中点をQとする。実数$x$,$y$に対して、直線OC上の点Xと、直線BC上の点Yを次のように定める。
$\overrightarrow{\textrm{OX}}$=$x\overrightarrow{\textrm{OC}}$, $\overrightarrow{\textrm{BY}}$=$y\overrightarrow{\textrm{BC}}$
このとき、直線QYと直線PXがねじれの位置にあるための$x$,$y$に関する必要十分条件を求めよ。
この動画を見る
$\Large\boxed{3}$ 座標空間の4点O,A,B,Cは同一平面上にないとする。線分OAの中点をP、線分ABの中点をQとする。実数$x$,$y$に対して、直線OC上の点Xと、直線BC上の点Yを次のように定める。
$\overrightarrow{\textrm{OX}}$=$x\overrightarrow{\textrm{OC}}$, $\overrightarrow{\textrm{BY}}$=$y\overrightarrow{\textrm{BC}}$
このとき、直線QYと直線PXがねじれの位置にあるための$x$,$y$に関する必要十分条件を求めよ。
#岡山県立大学 2023年 #Shorts
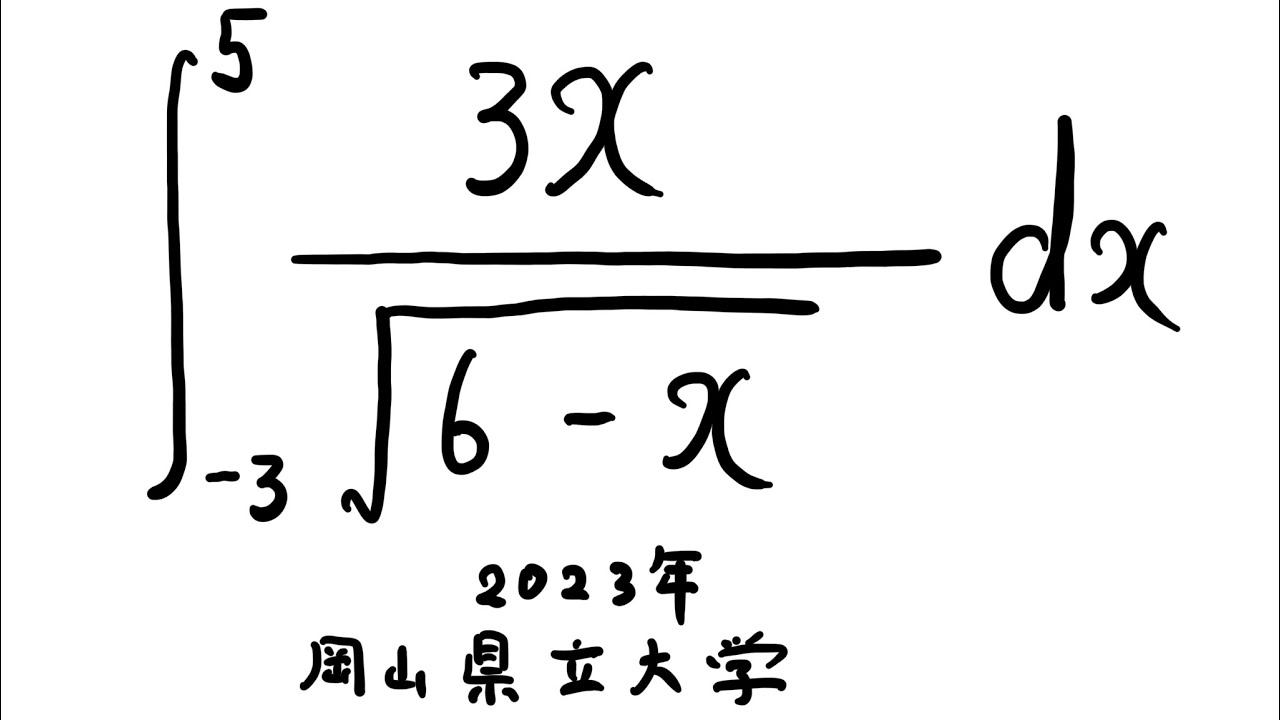
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-3}^{5} \displaystyle \frac{3x}{\sqrt{ 6-x }} dx$
出典:2023年岡山県立大学
この動画を見る
$\displaystyle \int_{-3}^{5} \displaystyle \frac{3x}{\sqrt{ 6-x }} dx$
出典:2023年岡山県立大学
【高校数学】毎日積分78日目~47都道府県制覇への道~【㉑奈良】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【奈良教育大学 2023】
以下の問いに答えよ。
(1) 次の関数の導関数を求めよ。ただし、対数は自然対数とする。
(i) $log|x+\sqrt{1+x^2}|$
(ii) $\displaystyle \frac{1}{2}(x\sqrt{1+x^2}+log|x+\sqrt{1+x^2}|)$
(2)次の等式を示せ。
$\displaystyle \int_0^{\frac{π}{2}}\frac{cos^3x}{\sqrt{1+sin^2x}}dx=\frac{1}{2}\{3log(1+\sqrt{2})-\sqrt{2}\}$
この動画を見る
【奈良教育大学 2023】
以下の問いに答えよ。
(1) 次の関数の導関数を求めよ。ただし、対数は自然対数とする。
(i) $log|x+\sqrt{1+x^2}|$
(ii) $\displaystyle \frac{1}{2}(x\sqrt{1+x^2}+log|x+\sqrt{1+x^2}|)$
(2)次の等式を示せ。
$\displaystyle \int_0^{\frac{π}{2}}\frac{cos^3x}{\sqrt{1+sin^2x}}dx=\frac{1}{2}\{3log(1+\sqrt{2})-\sqrt{2}\}$
大学入試問題#757「綺麗な基本問題」 東京理科大学(2001) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
関数$f(x)=1+\displaystyle \frac{1}{2}ce^{-x}$において、定数$c$は
$c=\displaystyle \int_{0}^{\frac{\pi}{2}} e^t f(t)\sin\ t\ dt$を満たす。
このとき、$c$の値を求めよ。
出典:2001年東京理科大学工学部 入試問題
この動画を見る
関数$f(x)=1+\displaystyle \frac{1}{2}ce^{-x}$において、定数$c$は
$c=\displaystyle \int_{0}^{\frac{\pi}{2}} e^t f(t)\sin\ t\ dt$を満たす。
このとき、$c$の値を求めよ。
出典:2001年東京理科大学工学部 入試問題
福田の数学〜京都大学2024年理系第2問〜複素数平面上における点の軌跡と領域

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $|x|$≦2 を満たす複素数$x$と、$|y-(8+6i)|$=3 を満たす複素数$y$に対して、$z$=$\displaystyle\frac{x+y}{2}$ とする。このような複素数$z$が複素数平面において動く領域を図示し、その面積を求めよ。
この動画を見る
$\Large\boxed{2}$ $|x|$≦2 を満たす複素数$x$と、$|y-(8+6i)|$=3 を満たす複素数$y$に対して、$z$=$\displaystyle\frac{x+y}{2}$ とする。このような複素数$z$が複素数平面において動く領域を図示し、その面積を求めよ。
大学入試問題#756「ほぼ定石通り」 藤田医科大学(2024) #級数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ na_{n+1}=3\displaystyle \sum_{k=1}^n a_k$
1.数列$\{a_n\}$の一般項を求めよ。
2.$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{a_{n+1}}{a_na_{n+2}}$を求めよ。
出典:2024年藤田医科大学 入試問題
この動画を見る
$a_1=1,\ na_{n+1}=3\displaystyle \sum_{k=1}^n a_k$
1.数列$\{a_n\}$の一般項を求めよ。
2.$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{a_{n+1}}{a_na_{n+2}}$を求めよ。
出典:2024年藤田医科大学 入試問題
見ただけで何でくくれるかは、わかる。 大学入試の因数分解 秋田大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x(x+1)(x+2)-y(y+1)(y+2)+xy(x-y)$
秋田大学
この動画を見る
因数分解せよ
$x(x+1)(x+2)-y(y+1)(y+2)+xy(x-y)$
秋田大学
大学入試問題#755「基本問題」 北海道大学(1970) #微分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)$は$x \gt 0$で定義された正の値をとる微分可能な関数で
$\{f(x)\}^2=x+1+\displaystyle \int_{1}^{x} \{f(t)\}^2dt$を満たすものとする。
(1)$y=f(x)$の満たす1階微分方程式を求めよ。
(2)$y=f(x)$を任意定数を含まない形で求めよ。
出典:1970年北海道大学 入試問題
この動画を見る
$f(x)$は$x \gt 0$で定義された正の値をとる微分可能な関数で
$\{f(x)\}^2=x+1+\displaystyle \int_{1}^{x} \{f(t)\}^2dt$を満たすものとする。
(1)$y=f(x)$の満たす1階微分方程式を求めよ。
(2)$y=f(x)$を任意定数を含まない形で求めよ。
出典:1970年北海道大学 入試問題
#岡山県立大学 2011 #定積分 #Shorts
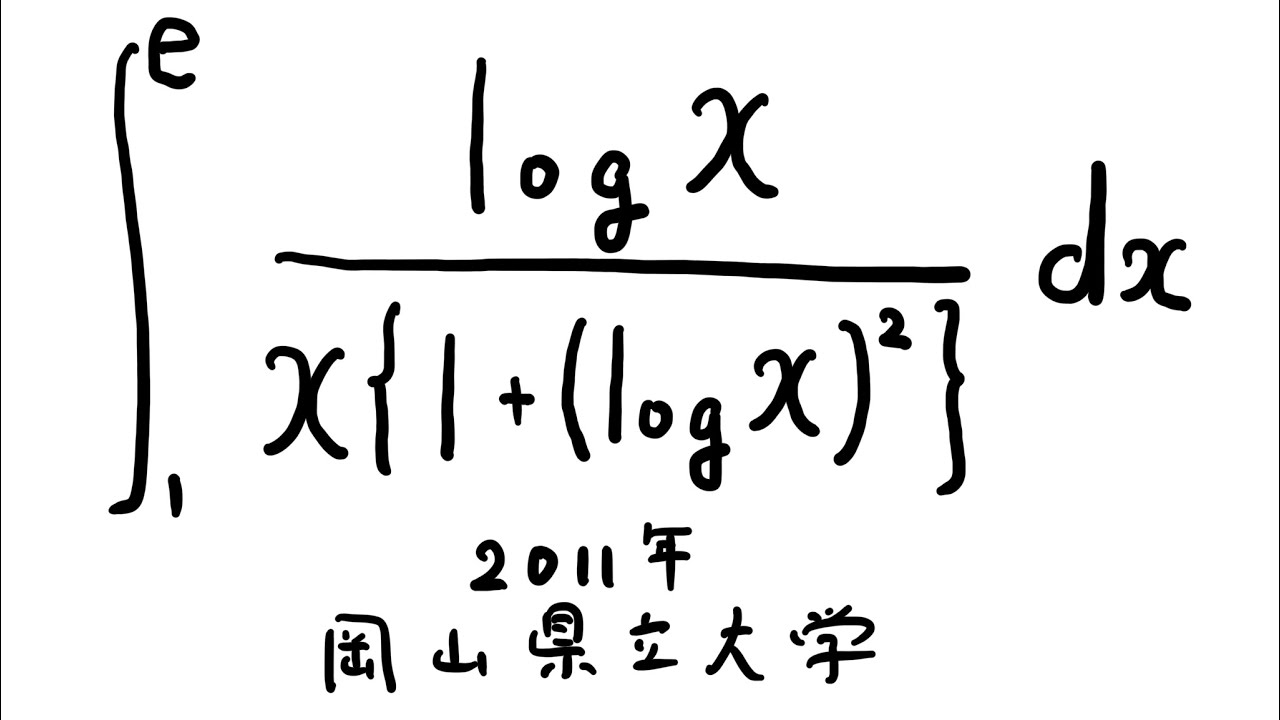
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x\{1+(log\ x)^2\}}dx$
出典:2011年岡山県立大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x\{1+(log\ x)^2\}}dx$
出典:2011年岡山県立大学
