 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
北里大学2021年医学部第1問(2)。複素数平面でド・モアブルの定理を利用した偏角、絶対値の計算や正三角形の残りの頂点を求める

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(2)iを虚数単位とし、$z_1=\frac{(\sqrt3+i)^{17}}{(1+i)^{19}(1-\sqrt3i)^7}, z_2=-1+i$とする。
$z_1$の偏角$\theta$のうち、$\\0 \leqq \theta \lt 2\pi$を満たすものは$\theta=\boxed{オ}$であり、$|z_1|=\boxed{カ}$である。
複素数平面上で$z_1,z_2$を表す点をそれぞれA,Bとする。このとき線分ABを
1辺とする正三角形ABCの、頂点Cを表す複素数の実部は0または$\boxed{キ}$である。
a,bを正の整数とし、複素数$\frac{(\sqrt3+i)^7}{(1+i)^a(1-\sqrt3i)^b}$の偏角の一つが$\frac{\pi}{12}$であるとき、
a+bの最小値は$\boxed{ク}$である。
2021北里大学医学部過去問
この動画を見る
(2)iを虚数単位とし、$z_1=\frac{(\sqrt3+i)^{17}}{(1+i)^{19}(1-\sqrt3i)^7}, z_2=-1+i$とする。
$z_1$の偏角$\theta$のうち、$\\0 \leqq \theta \lt 2\pi$を満たすものは$\theta=\boxed{オ}$であり、$|z_1|=\boxed{カ}$である。
複素数平面上で$z_1,z_2$を表す点をそれぞれA,Bとする。このとき線分ABを
1辺とする正三角形ABCの、頂点Cを表す複素数の実部は0または$\boxed{キ}$である。
a,bを正の整数とし、複素数$\frac{(\sqrt3+i)^7}{(1+i)^a(1-\sqrt3i)^b}$の偏角の一つが$\frac{\pi}{12}$であるとき、
a+bの最小値は$\boxed{ク}$である。
2021北里大学医学部過去問
福田の1.5倍速演習〜合格する重要問題021〜一橋大学2016年度文系数学第4問〜絶対値の付いた3次関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数とし、$f(x)=x^3-3ax$とする。区間$-1 \leqq x \leqq 1$における
$|f(x)|$の最大値をMとする。Mの最小値とそのときのaの値を求めよ。
2016一橋大学文系過去問
この動画を見る
aを実数とし、$f(x)=x^3-3ax$とする。区間$-1 \leqq x \leqq 1$における
$|f(x)|$の最大値をMとする。Mの最小値とそのときのaの値を求めよ。
2016一橋大学文系過去問
福田の1.5倍速演習〜合格する重要問題020〜東京工業大学2016年度理系数学第5問〜媒介変数で表された曲線の追跡と面積

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東京工業大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
次のように媒介変数表示されたxy平面上の曲線をCとする。
$\left\{\begin{array}{1}
x=3\cos t-\cos3t
y=3\sin t-\sin3t
\end{array}\right.$
ただし、$0 \leqq t \leqq \frac{\pi}{2}$である。
(1)$\frac{dx}{dt}$および$\frac{dy}{dt}$を計算し、Cの概形を図示せよ。
(2)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2016東京工業大学理系過去問
この動画を見る
次のように媒介変数表示されたxy平面上の曲線をCとする。
$\left\{\begin{array}{1}
x=3\cos t-\cos3t
y=3\sin t-\sin3t
\end{array}\right.$
ただし、$0 \leqq t \leqq \frac{\pi}{2}$である。
(1)$\frac{dx}{dt}$および$\frac{dy}{dt}$を計算し、Cの概形を図示せよ。
(2)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2016東京工業大学理系過去問
福田の数学〜北里大学2021年医学部第1問(1)〜空間ベクトルの内積と平面に下ろした垂線の長さ

単元:
#数Ⅰ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)一辺の長さが4の正四面体ABCDにおいて、辺BCの中点をEとおく。
動点Pは$PE=\frac{1}{2}AE$を満たしながら$\triangle AED$の内部および周上を動くものとし、
$\angle PED=\theta$とおく。このとき、$\overrightarrow{ PB }・\overrightarrow{ PC }=\boxed{ア}$である。また、$\overrightarrow{ PB }・\overrightarrow{ PC }$を
$\theta$を用いて表すと$\overrightarrow{ PC }・\overrightarrow{ PD }=\boxed{イ}$、その最大値は$\boxed{ウ}$である。
$\overrightarrow{ PC }・\overrightarrow{ PD }$が最大となるときの点Pと平面ACDの距離は$\boxed{エ}$である。
2021北里大学医学部過去問
この動画を見る
(1)一辺の長さが4の正四面体ABCDにおいて、辺BCの中点をEとおく。
動点Pは$PE=\frac{1}{2}AE$を満たしながら$\triangle AED$の内部および周上を動くものとし、
$\angle PED=\theta$とおく。このとき、$\overrightarrow{ PB }・\overrightarrow{ PC }=\boxed{ア}$である。また、$\overrightarrow{ PB }・\overrightarrow{ PC }$を
$\theta$を用いて表すと$\overrightarrow{ PC }・\overrightarrow{ PD }=\boxed{イ}$、その最大値は$\boxed{ウ}$である。
$\overrightarrow{ PC }・\overrightarrow{ PD }$が最大となるときの点Pと平面ACDの距離は$\boxed{エ}$である。
2021北里大学医学部過去問
福田の1.5倍速演習〜合格する重要問題019〜東京工業大学2016年度理系数学第4問〜整数に関する論証

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを2以上の自然数とする。
(1)nが素数または4のとき、$(n-1)!$はnで割り切れないことを示せ。
(2)nが素数でなくかつ4でもないとき、$(n-1)!$はnで割り切れることを示せ。
2016東京工業大学理系過去問
この動画を見る
nを2以上の自然数とする。
(1)nが素数または4のとき、$(n-1)!$はnで割り切れないことを示せ。
(2)nが素数でなくかつ4でもないとき、$(n-1)!$はnで割り切れることを示せ。
2016東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題018〜東北大学2016年度文系数学第3問〜3変数の不定方程式

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある工場で作る部品A,B,Cはねじをそれぞれ7個、9個、12個使っている。
出荷後に残ったこれらの部品のねじを全て外したところ、ネジが全部で54個あった。
残った部品A,B,Cの個数をそれぞれl,m,nとして可能性のある組(l,m,n)を全て求めよ。
2016東北大学文系過去問
この動画を見る
ある工場で作る部品A,B,Cはねじをそれぞれ7個、9個、12個使っている。
出荷後に残ったこれらの部品のねじを全て外したところ、ネジが全部で54個あった。
残った部品A,B,Cの個数をそれぞれl,m,nとして可能性のある組(l,m,n)を全て求めよ。
2016東北大学文系過去問
大学入試問題#384「見た目のイカツサはない計算量」 #富山県立大学2009 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x(1+log\ x)^2} dx$
出典:2009年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x(1+log\ x)^2} dx$
出典:2009年富山県立大学 入試問題
頻出!微分のよく見るような問題【京都大学】【数学 入試問題】
単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
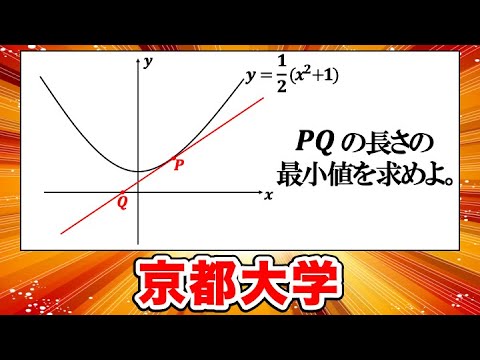
曲線$y=\displaystyle \frac{1}{2}(x^2+1)$上の点$P$における接線は$x$軸と交わるとし,その交点を$\varrho$とおく。線分$P\varrho$の長さを$L$とするとき,$L$が取りうる値の最小値を求めよ。
京都大過去問
この動画を見る
曲線$y=\displaystyle \frac{1}{2}(x^2+1)$上の点$P$における接線は$x$軸と交わるとし,その交点を$\varrho$とおく。線分$P\varrho$の長さを$L$とするとき,$L$が取りうる値の最小値を求めよ。
京都大過去問
頻出!微分のよく見るような問題【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
曲線y=-1/2(x²+1)上の点Pにおける接線はx軸と交わるとし,その交点をQとおく。線分PQの長さをLとするとき, Lが取りうる値の最小値を求めよ。
京都大過去問
この動画を見る
曲線y=-1/2(x²+1)上の点Pにおける接線はx軸と交わるとし,その交点をQとおく。線分PQの長さをLとするとき, Lが取りうる値の最小値を求めよ。
京都大過去問
福田の1.5倍速演習〜合格する重要問題017〜東北大学2016年度理系数学第6問〜定積分で表された関数

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数
$f(x)=\int_0^{\pi}|\sin(t-x)-\sin2t|dt$
の区間$\ 0 \leqq x \leqq \pi\ $における最大値と最小値を求めよ。
2016東北大学理系過去問
この動画を見る
関数
$f(x)=\int_0^{\pi}|\sin(t-x)-\sin2t|dt$
の区間$\ 0 \leqq x \leqq \pi\ $における最大値と最小値を求めよ。
2016東北大学理系過去問
大学入試問題#383「もう、この手法は擦りすぎか」 東洋大学2011 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東洋大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{\cos^2x}{2^x+1} dx$
出典:2011年東洋大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{\cos^2x}{2^x+1} dx$
出典:2011年東洋大学 入試問題
【数学】東京海洋大2021年度整数問題(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京海洋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自然数a,b,cが等式$a^2+b^2=c^2$を満たすときa,b,cの少なくとも一つは5の倍数であることを示せ
この動画を見る
自然数a,b,cが等式$a^2+b^2=c^2$を満たすときa,b,cの少なくとも一つは5の倍数であることを示せ
福田の1.5倍速演習〜合格する重要問題016〜京都大学2016年度理系数学第2問〜素数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学的帰納法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
この動画を見る
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
大学入試問題#382「初手が重要かと」 千葉大学 改 2009 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3\sqrt{ 3 }} \displaystyle \frac{1}{1+\sqrt[ 3 ]{ x^2 }} dx$
出典:2009年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3\sqrt{ 3 }} \displaystyle \frac{1}{1+\sqrt[ 3 ]{ x^2 }} dx$
出典:2009年千葉大学 入試問題
東大数学!少しひらめきを求められる問題です(誘導あり)【東京大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
この動画を見る
(1)実数$x$が$-1<x<1,x \neq 0$を満たすとき,次の不等式を示せ。
$(1-x)^{1-\dfrac{1}{x}}<(1+x)^{\dfrac{1}{x}}$
(2)次の不等式を示せ。
$0.9999^{101}<0.99<0.9999^{100}$
東大過去問
福田の1.5倍速演習〜合格する重要問題015〜東京大学2016年度理系数学第4問〜複素数平面上の三角形が鋭角三角形になる条件

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
zを複素数とする。複素数平面上の3点$A(I),B(z),C(z^2)$が
鋭角三角形をなすようなzの範囲を定め、図示せよ。
2016東京大学理系過去問
この動画を見る
zを複素数とする。複素数平面上の3点$A(I),B(z),C(z^2)$が
鋭角三角形をなすようなzの範囲を定め、図示せよ。
2016東京大学理系過去問
大学入試問題#381「ストック0でPC破損との闘い」 愛知工業大学2011 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} \displaystyle \frac{x^3+3x}{x^2+1} dx$
出典:2011年愛知工業大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2} \displaystyle \frac{x^3+3x}{x^2+1} dx$
出典:2011年愛知工業大学 入試問題
福田の1.5倍速演習〜合格する重要問題014〜東京大学2016年度理系数学第1問〜eの定義と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
eを自然対数の底、すなわち$e=\lim_{t \to \infty}\left(1+\frac{1}{t}\right)^t$とする。
すべての正の実数xに対し、次の不等式が成り立つことを示せ。
$\left(1+\frac{1}{x}\right)^x \lt e \lt \left(1+\frac{1}{x}\right)^{x+\frac{1}{2}}$
2016東京大学理系過去問
この動画を見る
eを自然対数の底、すなわち$e=\lim_{t \to \infty}\left(1+\frac{1}{t}\right)^t$とする。
すべての正の実数xに対し、次の不等式が成り立つことを示せ。
$\left(1+\frac{1}{x}\right)^x \lt e \lt \left(1+\frac{1}{x}\right)^{x+\frac{1}{2}}$
2016東京大学理系過去問
大学入試問題#380「基本に沿って」 立教大学2011 #極限
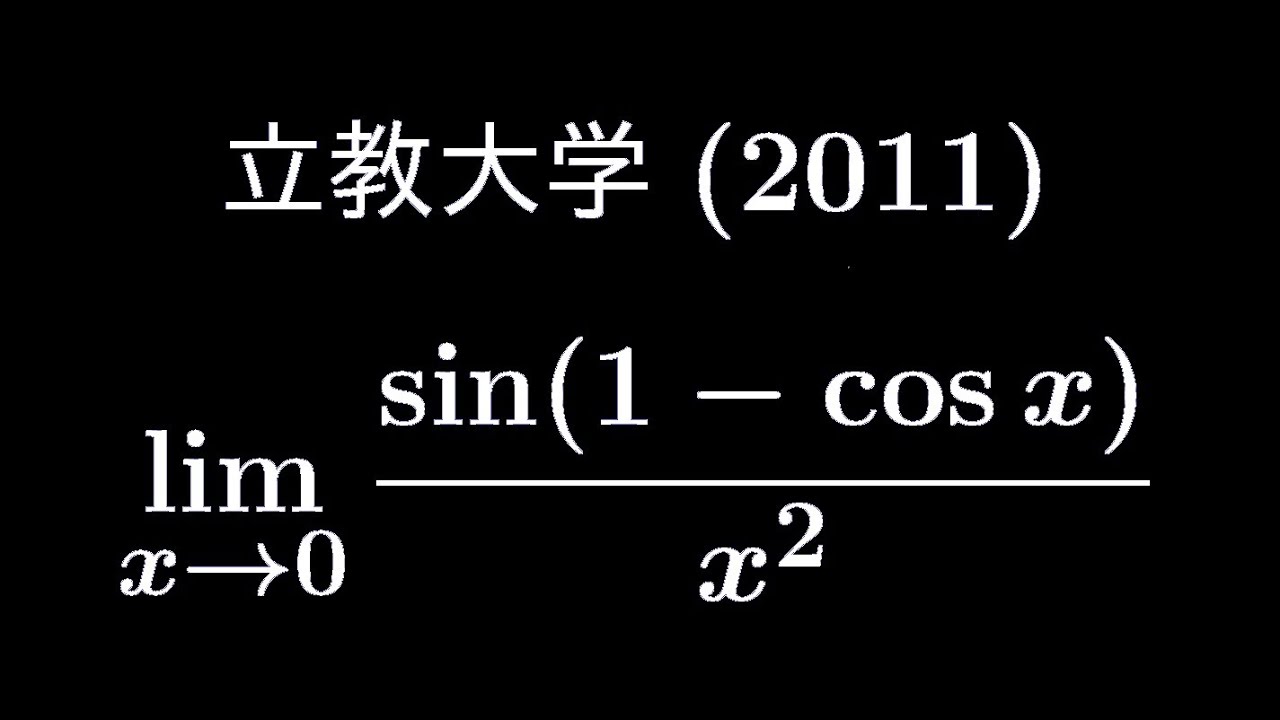
単元:
#大学入試過去問(数学)#関数と極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos\ x)}{x^2}$
出典:2011年立教大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos\ x)}{x^2}$
出典:2011年立教大学 入試問題
福田の1.5倍速演習〜合格する重要問題013〜京都大学2015年度理系数学第3問〜極限と追い出しの原理

単元:
#大学入試過去問(数学)#微分とその応用#数列の極限#微分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数とするとき、(a,0)を通り、$y=e^x+1$に接する直線がただ
一つ存在することを示せ。
(2)$a_1=1$として、$n=1,2,\cdots$について、$(a_n, 0)$を通り、$y=e^x+1$に接する
直線の接点のx座標を$a_{n+1}$とする。このとき、$\lim_{n \to \infty}(a_{n+1}-a_n)$を求めよ。
2015京都大学理系過去問
この動画を見る
aを実数とするとき、(a,0)を通り、$y=e^x+1$に接する直線がただ
一つ存在することを示せ。
(2)$a_1=1$として、$n=1,2,\cdots$について、$(a_n, 0)$を通り、$y=e^x+1$に接する
直線の接点のx座標を$a_{n+1}$とする。このとき、$\lim_{n \to \infty}(a_{n+1}-a_n)$を求めよ。
2015京都大学理系過去問
大学入試問題#379「計算が大変そうだが・・・」 同志社大学2011 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#同志社大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+5}{(x+1)^2(x-2)} dx$
出典:2011年同志社大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+5}{(x+1)^2(x-2)} dx$
出典:2011年同志社大学 入試問題
福田の1.5倍速演習〜合格する重要問題012〜京都大学2015年度文系数学第1問〜折れ線と交わらない条件

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次関数とグラフ#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
この動画を見る
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
数Ⅲ微分!絶対に落としたくない問題です【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x>0$に対して,$(1+x)^{\frac{1}{x}}<e<(1+x)^{\frac{1}{x}+1}$が成り立つことを示せ。
一橋大過去問
この動画を見る
$x>0$に対して,$(1+x)^{\frac{1}{x}}<e<(1+x)^{\frac{1}{x}+1}$が成り立つことを示せ。
一橋大過去問
福田の1.5倍速演習〜合格する重要問題011〜東京大学2015年度理系数学第5問〜コンビネーションの性質

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
mを2015以下の正の整数とする。
2015Cmが偶数となる最小のmを求めよ
2015東京大学理系過去問
この動画を見る
mを2015以下の正の整数とする。
2015Cmが偶数となる最小のmを求めよ
2015東京大学理系過去問
福田の1.5倍速演習〜合格する重要問題010〜千葉大学2015年度理系数学第6問〜論証と剰余類

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
この動画を見る
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
大学入試問題#378「どこまで記述すべきか・・・」 #奈良県立医科大学2015 #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin\ x-\sin(\tan\ x)}{x-\tan\ x}$
出典:2015年奈良県立医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin\ x-\sin(\tan\ x)}{x-\tan\ x}$
出典:2015年奈良県立医科大学 入試問題
東大医学部ベテランちが5浪TAWASHIに早稲田の数学の問題を解説

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
東大医学部のベテランちさんが、TAWASHIさんに早稲田大学の数学入試を解説します。
問題の解き方を理解しましょう!
この動画を見る
東大医学部のベテランちさんが、TAWASHIさんに早稲田大学の数学入試を解説します。
問題の解き方を理解しましょう!
福田の1.5倍速演習〜合格する重要問題009〜九州大学2015年度理系数学第2問〜関数の増減と区分求積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)関数$\ y=\frac{1}{x(\log x)^2}$は$x \gt 1$において単調に減少することを示せ。
(2)不定積分$\ \int\frac{1}{x(\log x)^2}dx$ を求めよ。
(3)nを3以上の整数とするとき、不等式
$\sum_{k=3}^n\frac{1}{k(\log k)^2} \lt \frac{1}{\log 2}$
が成り立つことを示せ。
2015九州大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)関数$\ y=\frac{1}{x(\log x)^2}$は$x \gt 1$において単調に減少することを示せ。
(2)不定積分$\ \int\frac{1}{x(\log x)^2}dx$ を求めよ。
(3)nを3以上の整数とするとき、不等式
$\sum_{k=3}^n\frac{1}{k(\log k)^2} \lt \frac{1}{\log 2}$
が成り立つことを示せ。
2015九州大学理系過去問
大学入試問題#377「基本的な手筋」 琉球大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1}|x|\sqrt{ 1-x^2 }\ dx$
出典:2015年琉球大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1}|x|\sqrt{ 1-x^2 }\ dx$
出典:2015年琉球大学 入試問題
対数と整数の融合問題!難問です【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\log_{y} (6x+y)=x$を満たす正の整数$x,y$の組を求めよ。
一橋大過去問
この動画を見る
$\log_{y} (6x+y)=x$を満たす正の整数$x,y$の組を求めよ。
一橋大過去問
