 式の計算(整式・展開・因数分解)
式の計算(整式・展開・因数分解)
 式の計算(整式・展開・因数分解)
式の計算(整式・展開・因数分解)
【数Ⅰ】相反方程式の解法(偶数次数の場合)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
相反方程式という特殊な方程式の解法を説明します。こちらの動画では定義の説明と、偶数次数の場合の解法を紹介しています。
この動画を見る
相反方程式という特殊な方程式の解法を説明します。こちらの動画では定義の説明と、偶数次数の場合の解法を紹介しています。
【数学Ⅰ/高1の予習】複雑な式の因数分解
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
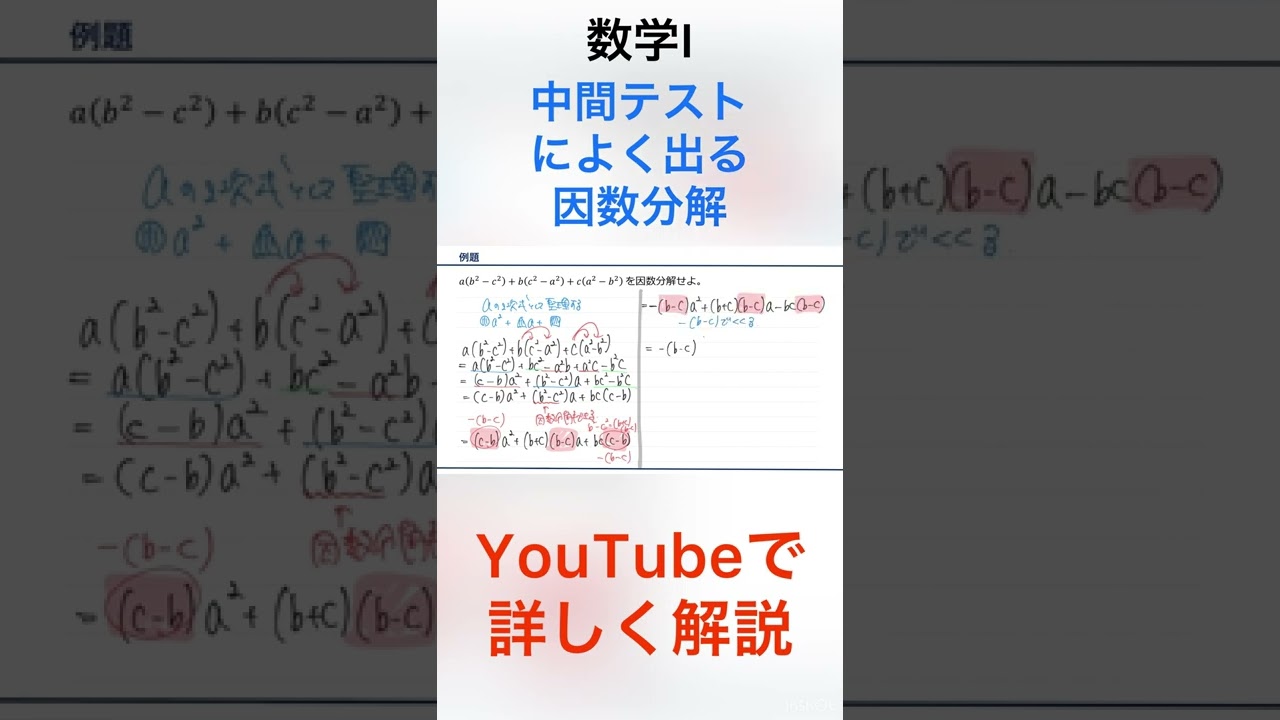
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
この動画を見る
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
【テストに出る】複雑な式の因数分解を解説!(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
この動画を見る
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
【#5】【因数分解100問】基礎から応用まで!(41)〜(50)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(41)$2xy-x-2y+1$
(42)$ab-bc+cd-da$
(43)$16-12y+3xy-x^2$
(44)$x^3y+x^2-xyz^2-z^2$
(45)$a^2+b^2+2bc+2ca+2ab$
(46)$(x+y+5)(x+2y-3)$
(47)$(x-y-2)(x-y+1)$
(48)$(2x+y+4)(3x+y-5)$
(49)$-(a-b)(b-c)(c-a)$
(50)$(a+1)(b+1)(c+1)$
この動画を見る
(41)$2xy-x-2y+1$
(42)$ab-bc+cd-da$
(43)$16-12y+3xy-x^2$
(44)$x^3y+x^2-xyz^2-z^2$
(45)$a^2+b^2+2bc+2ca+2ab$
(46)$(x+y+5)(x+2y-3)$
(47)$(x-y-2)(x-y+1)$
(48)$(2x+y+4)(3x+y-5)$
(49)$-(a-b)(b-c)(c-a)$
(50)$(a+1)(b+1)(c+1)$
【#4】【因数分解100問】基礎から応用まで!(31)〜(40)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(31)$(x^2+5)(x+3)(x-3)$
(32)$(x^2+1)(x+1)(x-1)$
(33)$(a+2b)(a-2b)(2a+3b)(2a-3b)$
(34)$3b^2(3a+2bc)(3a-2bc)$
(35)$\dfrac{1}{4}(2a+b-c)(2a-b+c)$
(36)$(5x+3)(25x^2-15x+9)$
(37)$(2x-3y)(4x^2+6xy+9y^2)$
(38)$(x-2)(x+1)(x-3)(x+2)$
(39)$(x+1)(x+3)(x+2)^2$
(40)$(x-1)^2(x^2-2x-4)$
この動画を見る
(31)$(x^2+5)(x+3)(x-3)$
(32)$(x^2+1)(x+1)(x-1)$
(33)$(a+2b)(a-2b)(2a+3b)(2a-3b)$
(34)$3b^2(3a+2bc)(3a-2bc)$
(35)$\dfrac{1}{4}(2a+b-c)(2a-b+c)$
(36)$(5x+3)(25x^2-15x+9)$
(37)$(2x-3y)(4x^2+6xy+9y^2)$
(38)$(x-2)(x+1)(x-3)(x+2)$
(39)$(x+1)(x+3)(x+2)^2$
(40)$(x-1)^2(x^2-2x-4)$
大学ではなく高校入試。2種類の解法

単元:
#計算と数の性質#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$2^{ 56 }$と$5^{ 24 }$どっちが大きい?
この動画を見る
$2^{ 56 }$と$5^{ 24 }$どっちが大きい?
【#3】【因数分解100問】基礎から応用まで!(21)〜(30)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(21)$x^2-4x+4-y^2$
(22)$x^2-y^2+6y-9$
(23)$4a^2-4b^2+4b-1$
(24)$x^2-2xy+y^2-4z^2$
(25)$(x+2)^2+7(x+2)+6$
(26)$(x+y)^2-x-y-12$
(27)$6(x-y)^2-5(x-y)-4$
(28)$(a+b)^2+10c(a+b)+25c^2$
(29)$(x+y+2)(x+y-3)-6$
(30)$(x+2y)(x+2y-2z)-8z^2$
この動画を見る
(21)$x^2-4x+4-y^2$
(22)$x^2-y^2+6y-9$
(23)$4a^2-4b^2+4b-1$
(24)$x^2-2xy+y^2-4z^2$
(25)$(x+2)^2+7(x+2)+6$
(26)$(x+y)^2-x-y-12$
(27)$6(x-y)^2-5(x-y)-4$
(28)$(a+b)^2+10c(a+b)+25c^2$
(29)$(x+y+2)(x+y-3)-6$
(30)$(x+2y)(x+2y-2z)-8z^2$
有名な高校入試解説できる?

単元:
#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$2^{ 56 }$と$5^{ 24 }$ どちらが大きい?
この動画を見る
$2^{ 56 }$と$5^{ 24 }$ どちらが大きい?
【#2】【因数分解100問】基礎から応用まで!(11)〜(20)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(11)$x^2+19x+48$
(12)$x^2-6x-27$
(13)$x^2+8xy-20y^2$
(14)$y^2-7xy+10x^2$
(15)$5a^2+7a+2$
(16)$2x^2-7x-15$
(17)$4a^2+23a-27$
(18)$12x^2-25x+12$
(19)$5a^2+13ab-6b^2$
(20)$6x^2-3xy-18y^2$
この動画を見る
(11)$x^2+19x+48$
(12)$x^2-6x-27$
(13)$x^2+8xy-20y^2$
(14)$y^2-7xy+10x^2$
(15)$5a^2+7a+2$
(16)$2x^2-7x-15$
(17)$4a^2+23a-27$
(18)$12x^2-25x+12$
(19)$5a^2+13ab-6b^2$
(20)$6x^2-3xy-18y^2$
【#1】【因数分解100問】基礎から応用まで!(1)〜(10)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$5a^2b^2-25a^3b$
(2)$x^2+x(y+z)$
(3)$a(a-3b)-7b(3b-a)$
(4)$x^2+16x+64$
(5)$27a^2+18a+3$
(6)$4-4x+x^2$
(7)$\dfrac{1}{4}x^2-x+1$
(8)$4a^2-b^2$
(9)$9a^2-9b^2$
(10)$5a^3-20ab^2$
この動画を見る
(1)$5a^2b^2-25a^3b$
(2)$x^2+x(y+z)$
(3)$a(a-3b)-7b(3b-a)$
(4)$x^2+16x+64$
(5)$27a^2+18a+3$
(6)$4-4x+x^2$
(7)$\dfrac{1}{4}x^2-x+1$
(8)$4a^2-b^2$
(9)$9a^2-9b^2$
(10)$5a^3-20ab^2$
【数学Ⅰ/高1の予習】展開の公式を利用する因数分解
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
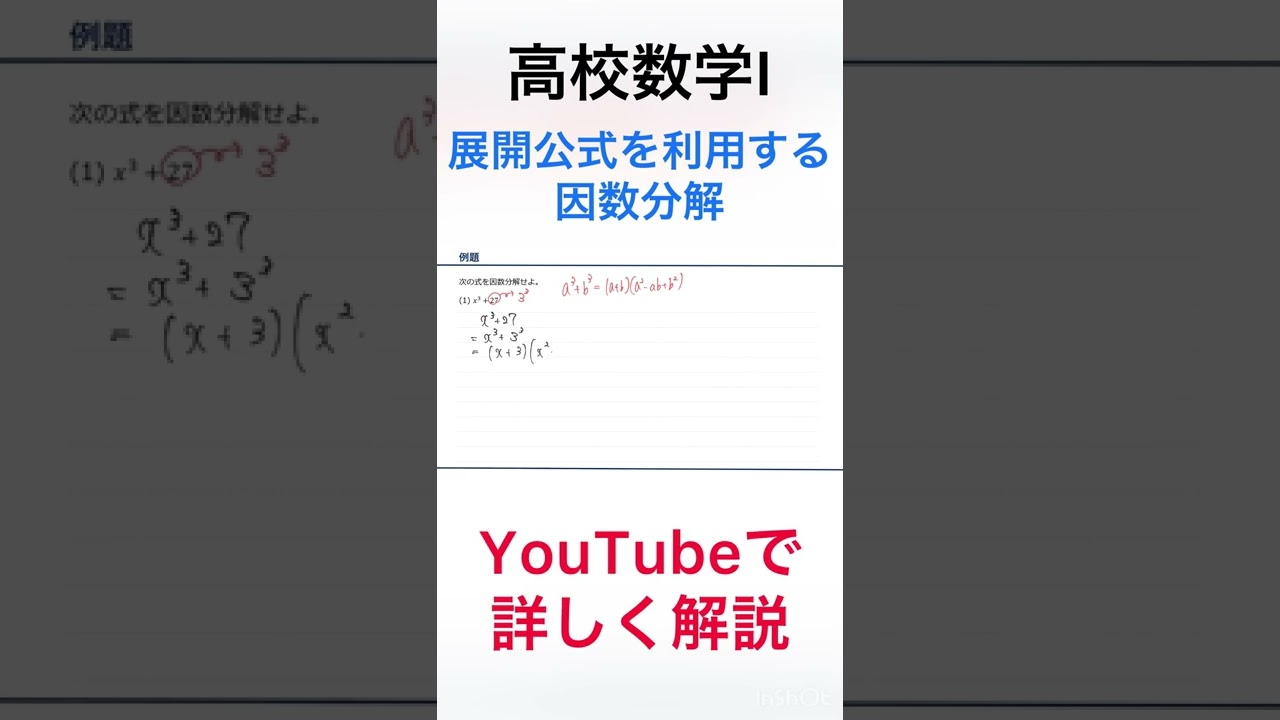
次の式を因数分解せよ。
(1)$x^3+27$
(2)$16x^3-2y^3$
(3)$x^3-9x^2+27x-27$
この動画を見る
次の式を因数分解せよ。
(1)$x^3+27$
(2)$16x^3-2y^3$
(3)$x^3-9x^2+27x-27$
【数学I/高1の予習】文字を含んだたすきがけの因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を因数分解せよ。
(1)$x^2+3xy+2y^2+4x+7y+3$
(2)$2x^2+5xy-3y^2+3x+2y+1$
この動画を見る
次の式を因数分解せよ。
(1)$x^2+3xy+2y^2+4x+7y+3$
(2)$2x^2+5xy-3y^2+3x+2y+1$
春は因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを因数分解せよ.
(1)$ x^2+y^2-x^2y^2-4xy-1 $
(2)$ x^2-y^2-2x+6y-8 $
この動画を見る
これを因数分解せよ.
(1)$ x^2+y^2-x^2y^2-4xy-1 $
(2)$ x^2-y^2-2x+6y-8 $
【数学Ⅰ/高1の予習】3乗の展開公式
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
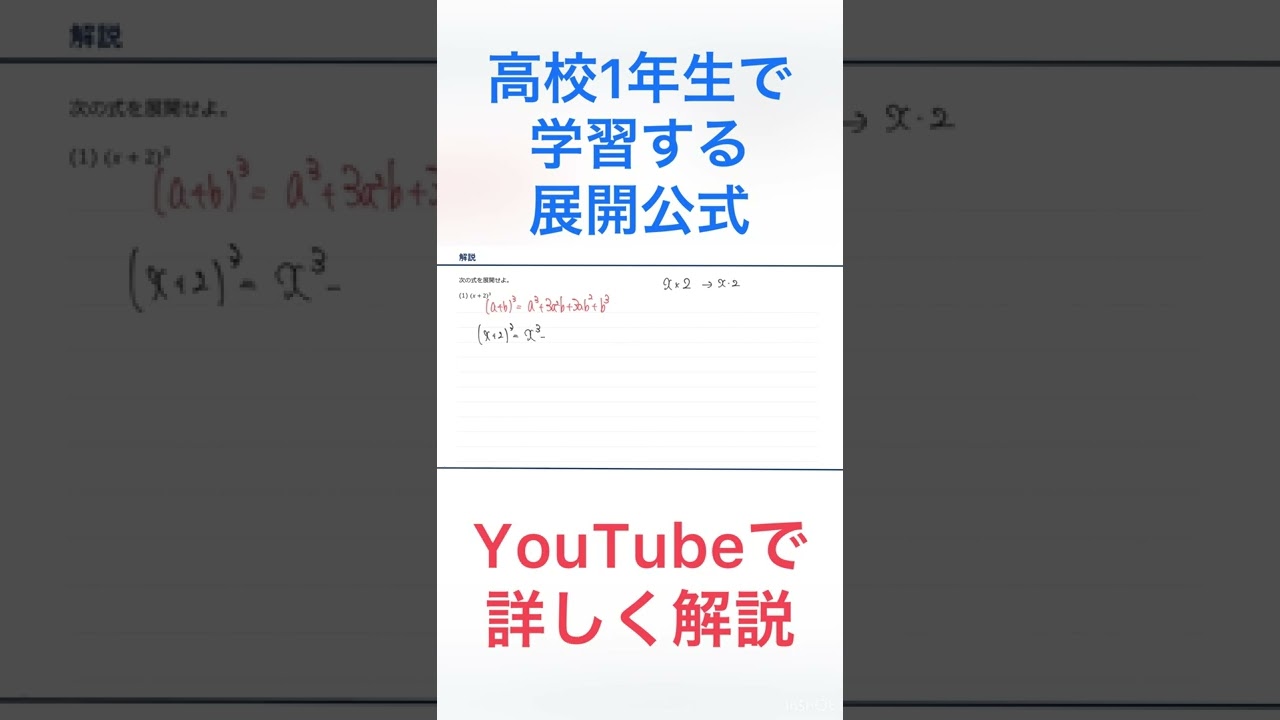
次の式を展開せよ。
(1)$(x+2)^3$
(2)$(3x-1)^3$
(3)$(2a-3b)^3$
この動画を見る
次の式を展開せよ。
(1)$(x+2)^3$
(2)$(3x-1)^3$
(3)$(2a-3b)^3$
【基礎から解説】展開の公式を利用する因数分解(高校数学Ⅰ)
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を因数分解せよ。
(1)$x^3+27$
(2)$16x^3-2y^3$
(3)$x^3-9x^2+27x-27$
この動画を見る
次の式を因数分解せよ。
(1)$x^3+27$
(2)$16x^3-2y^3$
(3)$x^3-9x^2+27x-27$
【数学Ⅰ/高1の予習】展開公式
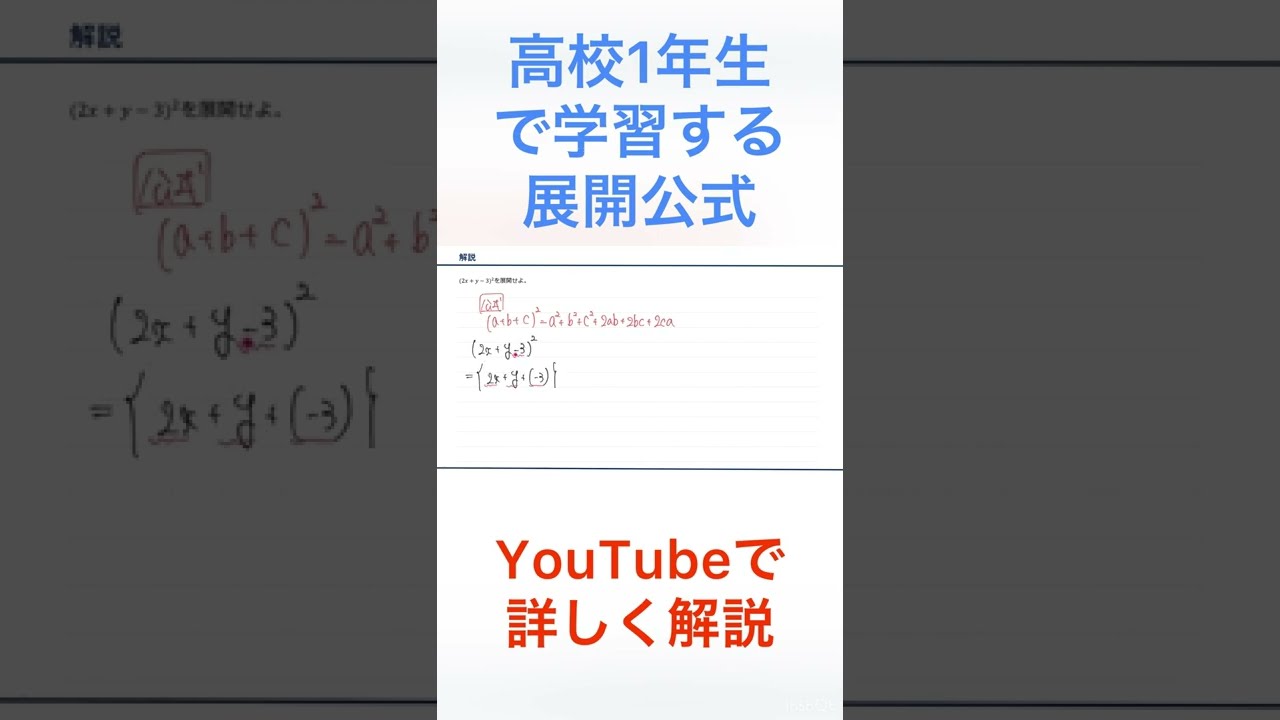
【わかりやすく】たすきがけを使う因数分解を解説!(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を因数分解せよ。
(1)$6x^2+7x+2$
(2)$2x^2+x-6$
(3)$3x^2-10xy+8y^2$
この動画を見る
次の式を因数分解せよ。
(1)$6x^2+7x+2$
(2)$2x^2+x-6$
(3)$3x^2-10xy+8y^2$
素数

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^4-11n^2+49 $が素数となる整数 $ n$を求めよ.
この動画を見る
$ n^4-11n^2+49 $が素数となる整数 $ n$を求めよ.
大学入試問題#143 東海大学医学部(2020) 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典:2020年東海大学医学部 入試問題
この動画を見る
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典:2020年東海大学医学部 入試問題
ただの因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+$
$x^3+x^2+x+1$
これを因数分解せよ.(実数係数)
この動画を見る
$ x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+$
$x^3+x^2+x+1$
これを因数分解せよ.(実数係数)
ただの因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+$
$x^3+x^2+x+1$
これを因数分解せよ.(実数係数)
この動画を見る
$ x^{11}+x^{10}+x^9+x^8+x^7+x^6+x^5+x^4+$
$x^3+x^2+x+1$
これを因数分解せよ.(実数係数)
【わかりやすく】高校で習う展開公式②(高校数学Ⅰ)

連立2元9次方程式
単元:
#数Ⅰ#数Ⅱ#数と式#2次関数#複素数と方程式#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4y^5+x^5y^4=810 \\
x^3y^6+x^6y^3=945
\end{array}
\right.
\end{eqnarray}$
実数解を求めよ.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4y^5+x^5y^4=810 \\
x^3y^6+x^6y^3=945
\end{array}
\right.
\end{eqnarray}$
実数解を求めよ.
【わかりやすく】高校で習う展開公式①(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を展開せよ。
(1)$(x+2)(x^2-2x+4)$
(2)$(x-3y)(x^2+3xy+9y^2)$
この動画を見る
次の式を展開せよ。
(1)$(x+2)(x^2-2x+4)$
(2)$(x-3y)(x^2+3xy+9y^2)$
【ゼロからわかる】3乗の展開公式(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を展開せよ。
(1)$(x+2)^3$
(2)$(3x-1)^3$
(3)$(2a-3b)^3$
この動画を見る
次の式を展開せよ。
(1)$(x+2)^3$
(2)$(3x-1)^3$
(3)$(2a-3b)^3$
【わかりやすく解説】中学の「展開」をおさらい!

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を展開せよ
(1)$(x+3)(2x-1)$
(2)$(x+3y)(x-3y)$
(3)$(x-5y)^2$
この動画を見る
次の式を展開せよ
(1)$(x+3)(2x-1)$
(2)$(x+3y)(x-3y)$
(3)$(x-5y)^2$
【本当に苦手な人へ8分だけ時間をください!!】因数分解の基礎を現役塾講師が簡単に解説!〔現役塾講師解説、数学〕

無題

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
この動画を見る
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
xの2022乗の値
単元:
#数Ⅰ#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \left(x+\dfrac{1}{x}\right)^2=3$のとき,$ x^{2022}$の値を求めよ.
この動画を見る
$ \left(x+\dfrac{1}{x}\right)^2=3$のとき,$ x^{2022}$の値を求めよ.
小数第2022位の数は?!

単元:
#数Ⅰ#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (6+\sqrt{37})^{2023}$の小数第$2022$位数は?
この動画を見る
$ (6+\sqrt{37})^{2023}$の小数第$2022$位数は?
