 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
2021年藤田医科大

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は実数である.
$\left(\dfrac{2+\sqrt{-77}}{9}\right)^{2021}=\dfrac{x+y\sqrt{-77}}{9}$
$x^2+77y^2$の値を求めよ.
2021藤田医科大過去問
この動画を見る
$x,y$は実数である.
$\left(\dfrac{2+\sqrt{-77}}{9}\right)^{2021}=\dfrac{x+y\sqrt{-77}}{9}$
$x^2+77y^2$の値を求めよ.
2021藤田医科大過去問
秘技!瞬間平方完成
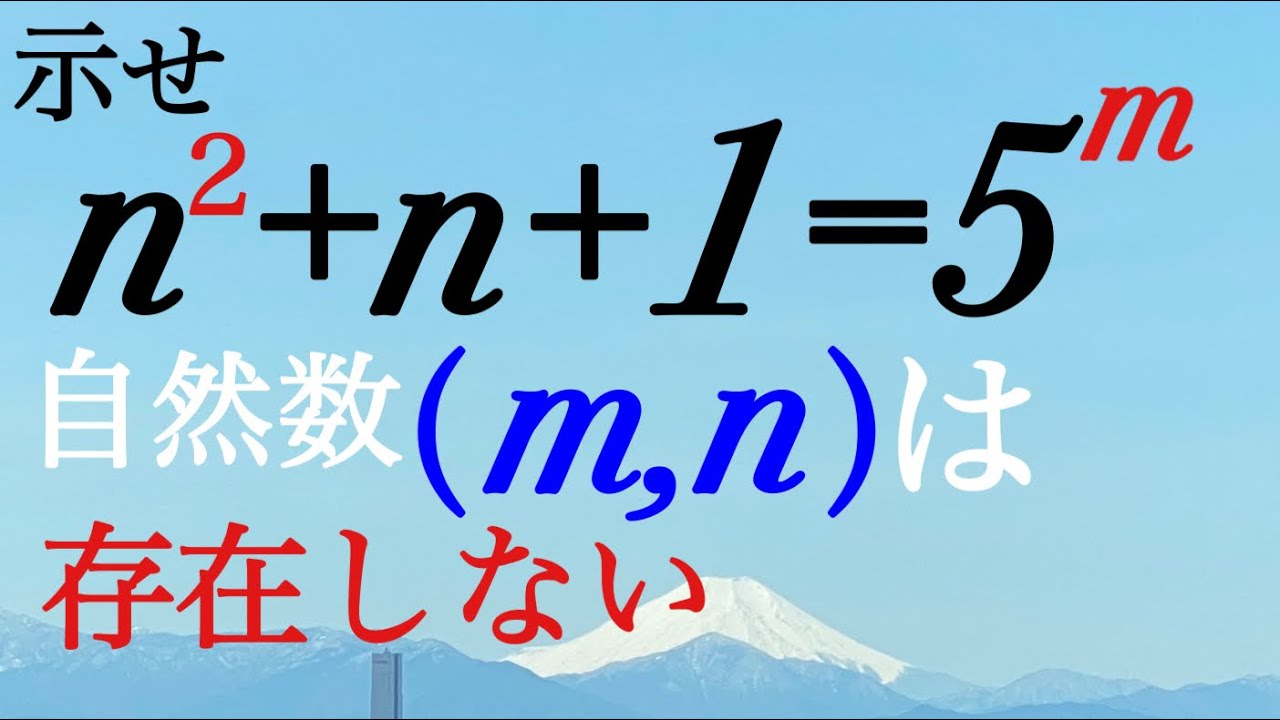
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^2+n+1=5^m$を満たす自然数$(m,n)$は存在しないことを示せ.
この動画を見る
$n^2+n+1=5^m$を満たす自然数$(m,n)$は存在しないことを示せ.
これは無理数か?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{97-56\sqrt3}+\sqrt{73+40\sqrt3}$は無理数か?
この動画を見る
$\sqrt{97-56\sqrt3}+\sqrt{73+40\sqrt3}$は無理数か?
平方根の計算 A コメント欄に良い解説あり!

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{1}{\sqrt 2} - \frac{1}{\sqrt 3})(\frac{1}{\sqrt 6} + \frac{1}{3})=$
日比谷高等学校
この動画を見る
$(\frac{1}{\sqrt 2} - \frac{1}{\sqrt 3})(\frac{1}{\sqrt 6} + \frac{1}{3})=$
日比谷高等学校
数理クイズ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
数理クイズ.これを解け.
$5\times 5=23$
$6\times 6=33$
$7\times 7=45$
$8\times 8=59$
$ 9\times 9=?$
$ 10\times 10=100$
この動画を見る
数理クイズ.これを解け.
$5\times 5=23$
$6\times 6=33$
$7\times 7=45$
$8\times 8=59$
$ 9\times 9=?$
$ 10\times 10=100$
4つの相加相乗平均

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,d$を正とする.
$\dfrac{a+b+c+d}{4}\geqq \sqrt[4]{abcd}$を示し,それを用いて$\dfrac{a+b+c}{3}\geqq \sqrt[3]{abc}$を示せ.
この動画を見る
$a,b,c,d$を正とする.
$\dfrac{a+b+c+d}{4}\geqq \sqrt[4]{abcd}$を示し,それを用いて$\dfrac{a+b+c}{3}\geqq \sqrt[3]{abc}$を示せ.
2021の2021乗根と2020の2020乗根どっちがでかい

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[2021]{2021}$と$\sqrt[2020]{2020}$では,どちらが大きいか?
この動画を見る
$\sqrt[2021]{2021}$と$\sqrt[2020]{2020}$では,どちらが大きいか?
平方根の方程式
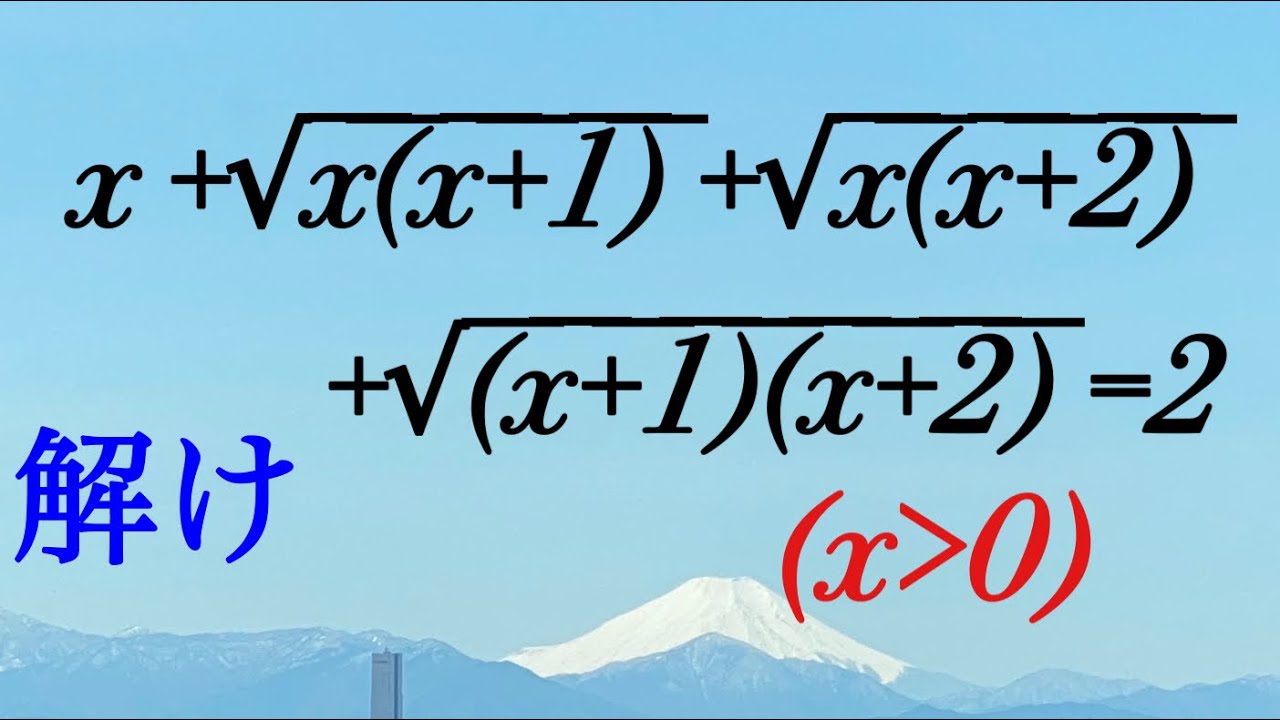
単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
方程式を解け.$x$は正の実数である.
$x+\sqrt{x(x+1)}+\sqrt{x(x+2)}+$
$\sqrt{(x+1)(x+2)}=2$
この動画を見る
方程式を解け.$x$は正の実数である.
$x+\sqrt{x(x+1)}+\sqrt{x(x+2)}+$
$\sqrt{(x+1)(x+2)}=2$
2021 ガウス記号

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(45+\sqrt{2021})^{2021}]$の$1$の位の数を求めよ.
この動画を見る
$[(45+\sqrt{2021})^{2021}]$の$1$の位の数を求めよ.
3乗根の大小

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[3]{26}$と$\sqrt[3]{28}$では,どちらが$3$に近いか.
この動画を見る
$\sqrt[3]{26}$と$\sqrt[3]{28}$では,どちらが$3$に近いか.
横浜市立大(医)3次方程式の虚数解の絶対値

単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-x^2-x+k=0(k\gt 1)$である.
(1)実数解は1個であることを示せ.
(2)3つの解の絶対値はいずれも1より大きいことを示せ.
横浜市立(医)過去問
この動画を見る
$x^3-x^2-x+k=0(k\gt 1)$である.
(1)実数解は1個であることを示せ.
(2)3つの解の絶対値はいずれも1より大きいことを示せ.
横浜市立(医)過去問
平方根:代表的な無理数の暗記法~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根:代表的な無理数の暗記法~全国入試問題解法
$\sqrt{ 2 } = 1.41421356$ 一夜一夜に人見ごろ
$\sqrt{ 3 } = 1.7320508$ ...人なみにおごれや
$\sqrt{ 5 } = 2.2360679$ 富士山ろくオウム鳴く
$\sqrt{ 6 } = 2 2.4494897$... 二夜シクシク
$\sqrt{ 7 } = 2 2.6457513$... 変に虫いないさ
$\sqrt{ 8 } = 2 2.828427$… ニヤニヤ呼ぶな
$\sqrt{ 10 } = 3 3,1622776.$……… 人丸は三色に並ぶや
この動画を見る
平方根:代表的な無理数の暗記法~全国入試問題解法
$\sqrt{ 2 } = 1.41421356$ 一夜一夜に人見ごろ
$\sqrt{ 3 } = 1.7320508$ ...人なみにおごれや
$\sqrt{ 5 } = 2.2360679$ 富士山ろくオウム鳴く
$\sqrt{ 6 } = 2 2.4494897$... 二夜シクシク
$\sqrt{ 7 } = 2 2.6457513$... 変に虫いないさ
$\sqrt{ 8 } = 2 2.828427$… ニヤニヤ呼ぶな
$\sqrt{ 10 } = 3 3,1622776.$……… 人丸は三色に並ぶや
富山大(医) 無理数の証明

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$は異なる素数であり,$k,m,n$は整数である.
$k+m\sqrt p+n\sqrt q=0$なら,$k=m=n=0$を示せ.
(1)$\sqrt p$が無理数であることを示せ.
2016富山大(医)
この動画を見る
$p,q$は異なる素数であり,$k,m,n$は整数である.
$k+m\sqrt p+n\sqrt q=0$なら,$k=m=n=0$を示せ.
(1)$\sqrt p$が無理数であることを示せ.
2016富山大(医)
北海道医療大(薬・歯)式の計算

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\dfrac{\sqrt5-1}{2}$である.
$\dfrac{1}{a}+\dfrac{1}{a^3}+\dfrac{1}{a^5}+\dfrac{1}{a^7}$の値を求めよ.
北海道医療大(薬・歯)過去問
この動画を見る
$a=\dfrac{\sqrt5-1}{2}$である.
$\dfrac{1}{a}+\dfrac{1}{a^3}+\dfrac{1}{a^5}+\dfrac{1}{a^7}$の値を求めよ.
北海道医療大(薬・歯)過去問
大阪市立大 無理数の証明
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
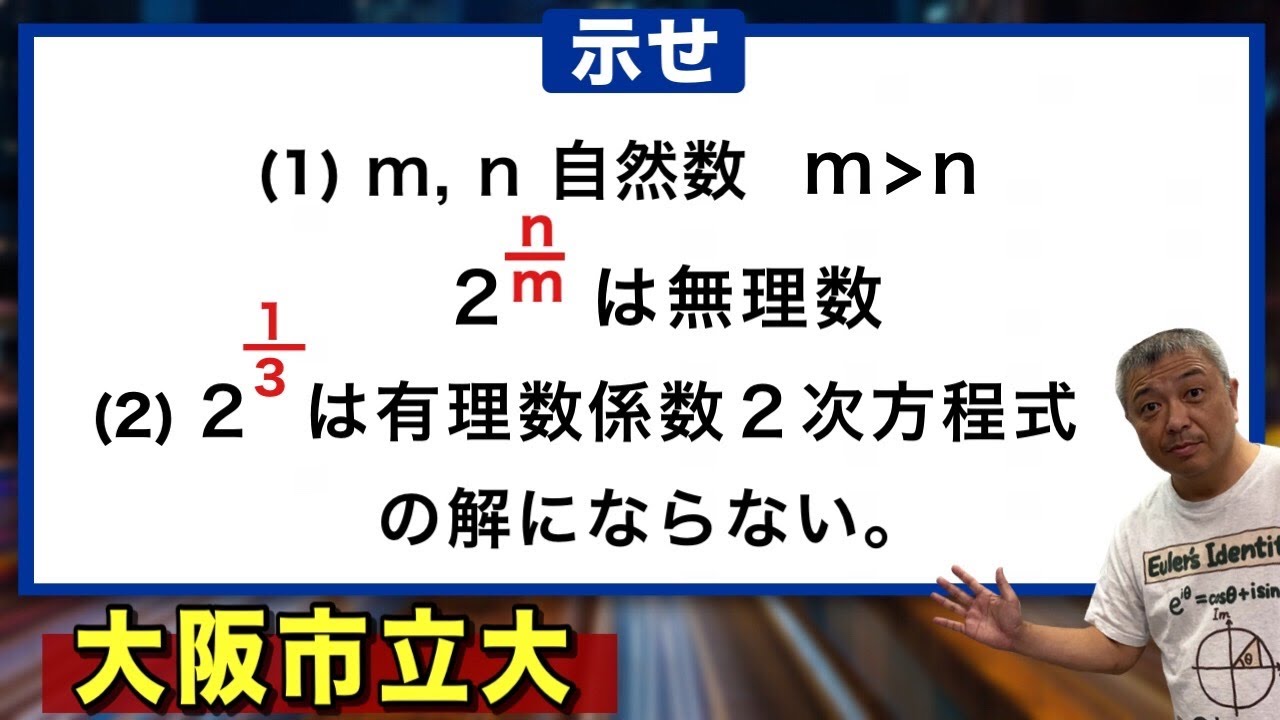
(1)$m,n$を自然数とし,$m\gt n$とする.$2^{\frac{n}{m}}$は無理数であることを示せ.
(2)$2^{\frac{1}{3}}$は有理数係数の2次方程式の解にならないことを示せ.
1993大阪市立大過去問
この動画を見る
(1)$m,n$を自然数とし,$m\gt n$とする.$2^{\frac{n}{m}}$は無理数であることを示せ.
(2)$2^{\frac{1}{3}}$は有理数係数の2次方程式の解にならないことを示せ.
1993大阪市立大過去問
数と式の全パターン①【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
1.次の式の分母を有理化せよ。
$\displaystyle \frac{1}{1+\sqrt{ 2 }+\sqrt{ 3 }}$
2.次の問いに答えよ。
$x=\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }}{\sqrt{ 5 }-\sqrt{ 3 }},\ y=\displaystyle \frac{\sqrt{ 5 }-\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}$のとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3$
(5)$x^4+y^4$
(6)$x^5+y^5$
3.次の問いに答えよ。
$x+\displaystyle \frac{1}{x}=3$のとき、次の式の値を求めよ。
(1)$x^2+\displaystyle \frac{1}{x^2}$
(2)$x-\displaystyle \frac{1}{x}$
(3)$x-^3+\displaystyle \frac{1}{x^3}$
(4)$x^4+\displaystyle \frac{1}{x^4}$
この動画を見る
1.次の式の分母を有理化せよ。
$\displaystyle \frac{1}{1+\sqrt{ 2 }+\sqrt{ 3 }}$
2.次の問いに答えよ。
$x=\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }}{\sqrt{ 5 }-\sqrt{ 3 }},\ y=\displaystyle \frac{\sqrt{ 5 }-\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}$のとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3$
(5)$x^4+y^4$
(6)$x^5+y^5$
3.次の問いに答えよ。
$x+\displaystyle \frac{1}{x}=3$のとき、次の式の値を求めよ。
(1)$x^2+\displaystyle \frac{1}{x^2}$
(2)$x-\displaystyle \frac{1}{x}$
(3)$x-^3+\displaystyle \frac{1}{x^3}$
(4)$x^4+\displaystyle \frac{1}{x^4}$
数と式の全パターン②【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
$\displaystyle \frac{1}{3-\sqrt{ 5 }}$の整数部分を$a$、小数部分を$b$とする。
(1)$a,b$の値を求めよ。
(2)$b^1+\displaystyle \frac{1}{2}b$の値を求めよ。
ーーーーーーーーーーーーーーーーーーーーーー
$x=\sqrt{ 2 }-1$のとき
$x^2+4x^2+3x^2+2x+1$
ーーーーーーーーーーーーーーーーーーーーーー
次の式の二重根号をはずして簡単にせよ。
(1)$\sqrt{ 5+2\sqrt{ 6 } }$
(2)$\sqrt{ 7-4\sqrt{ 3 } }$
(3)$\sqrt{ 8+\sqrt{ 60 } }$
(4)$\sqrt{ 3+\sqrt{ 5 } }$
この動画を見る
次の問いに答えよ。
$\displaystyle \frac{1}{3-\sqrt{ 5 }}$の整数部分を$a$、小数部分を$b$とする。
(1)$a,b$の値を求めよ。
(2)$b^1+\displaystyle \frac{1}{2}b$の値を求めよ。
ーーーーーーーーーーーーーーーーーーーーーー
$x=\sqrt{ 2 }-1$のとき
$x^2+4x^2+3x^2+2x+1$
ーーーーーーーーーーーーーーーーーーーーーー
次の式の二重根号をはずして簡単にせよ。
(1)$\sqrt{ 5+2\sqrt{ 6 } }$
(2)$\sqrt{ 7-4\sqrt{ 3 } }$
(3)$\sqrt{ 8+\sqrt{ 60 } }$
(4)$\sqrt{ 3+\sqrt{ 5 } }$
金沢大 N進法の循環小数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#金沢大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は1桁の自然数とする.
$N=\boxed{x}\boxed{y}.\boxed{z}_{(5)}$,$N-1=\boxed{z}\boxed{y}.\boxed{x}_{(7)}$
$(x,y,z)$の値を求めよ.
1969金沢大過去問
この動画を見る
$x,y,z$は1桁の自然数とする.
$N=\boxed{x}\boxed{y}.\boxed{z}_{(5)}$,$N-1=\boxed{z}\boxed{y}.\boxed{x}_{(7)}$
$(x,y,z)$の値を求めよ.
1969金沢大過去問
一橋大(2)
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
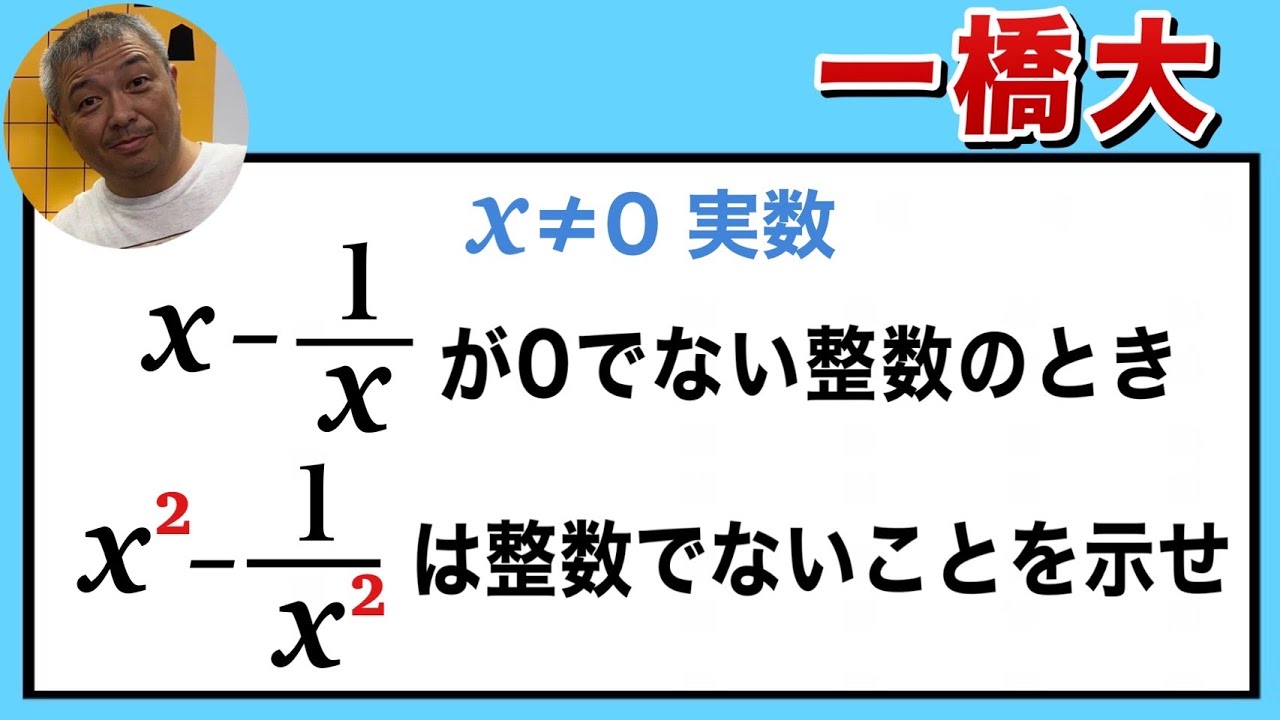
$x\neq 0$は実数である.
$x-\dfrac{1}{x}$が$0$でない整数であるとき,$x^2-\dfrac{1}{x^2}$は整数出ないことを示せ.
1991一橋大過去問
この動画を見る
$x\neq 0$は実数である.
$x-\dfrac{1}{x}$が$0$でない整数であるとき,$x^2-\dfrac{1}{x^2}$は整数出ないことを示せ.
1991一橋大過去問
3通り以上の平方の和で表せる数

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1^2+8^2=4^2+7^2=65$
$65$は2通りの平方の和で表せる.3通り以上の平方の和で表せる数の列をあげよ.
この動画を見る
$1^2+8^2=4^2+7^2=65$
$65$は2通りの平方の和で表せる.3通り以上の平方の和で表せる数の列をあげよ.
平方数の和

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2+b^2=13^5$を満たす自然数$(a,b)$の組を1つ例示せよ.
※平方数の和の積は平方数の和で表せる.
この動画を見る
$a^2+b^2=13^5$を満たす自然数$(a,b)$の組を1つ例示せよ.
※平方数の和の積は平方数の和で表せる.
名古屋大 分野不明

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{n}$は整数でなく,小数第一位が$0$で$2$倍は$0$でない.
$\sqrt{n}=\boxed{A}.0\boxed{b}・・・$
(1)最小の$n$を求めよ.
(2)小さい順で$10$番目の$n$を求めよ.
2019名古屋大過去問
この動画を見る
$\sqrt{n}$は整数でなく,小数第一位が$0$で$2$倍は$0$でない.
$\sqrt{n}=\boxed{A}.0\boxed{b}・・・$
(1)最小の$n$を求めよ.
(2)小さい順で$10$番目の$n$を求めよ.
2019名古屋大過去問
【数Ⅰ】数と式:√(4+√7)の2重根号を外す!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{(4+\sqrt7)}$の2重根号を外しなさい
この動画を見る
$\sqrt{(4+\sqrt7)}$の2重根号を外しなさい
【数Ⅰ】数と式:√(8+4√3)の2重根号を外す!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{(8+4\sqrt3)}$の2重根号を外しなさい
この動画を見る
$\sqrt{(8+4\sqrt3)}$の2重根号を外しなさい
【数Ⅰ】数と式:√(8-2√15)の2重根号を外す!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{(8-2\sqrt{15})}$の2重根号を外しなさい
この動画を見る
$\sqrt{(8-2\sqrt{15})}$の2重根号を外しなさい
大阪大 共役な無理数

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^n+a_{n-1}x^{n-1}+・・・・・・+a_1x+a_0=0$という$x$の$n$次方程式が
$1+\sqrt3$を解にもつとき$1-\sqrt3$も解であることを示せ.
$a_i(i=0$~$n-1$)は有理数である.
2009大阪大(改)過去問
この動画を見る
$x^n+a_{n-1}x^{n-1}+・・・・・・+a_1x+a_0=0$という$x$の$n$次方程式が
$1+\sqrt3$を解にもつとき$1-\sqrt3$も解であることを示せ.
$a_i(i=0$~$n-1$)は有理数である.
2009大阪大(改)過去問
大阪大 無理数と整数

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha$を$x^2-2x-1=0$の解とするとき,
$(a+5\alpha)(b+5c\alpha)=1$を満たす整数の組$(a,b,c)$をすべて求めよ.
ただし,$\sqrt2$が無理数であることは証明不要
2009大阪大過去問
この動画を見る
$\alpha$を$x^2-2x-1=0$の解とするとき,
$(a+5\alpha)(b+5c\alpha)=1$を満たす整数の組$(a,b,c)$をすべて求めよ.
ただし,$\sqrt2$が無理数であることは証明不要
2009大阪大過去問
慶應義塾大 3次方程式が有理数解をもつ条件

単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^3-(a+1)x^2-4x+a=0$が整数でない有理数解をもつ自然数$a$の値を求めよ.
慶應義塾大過去問
この動画を見る
$3x^3-(a+1)x^2-4x+a=0$が整数でない有理数解をもつ自然数$a$の値を求めよ.
慶應義塾大過去問
16大阪府教員採用試験(数学:高校1番 積分)

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1⃣ $f(x)=\int_1^e |logt-logx|dt (1 \leqq x \leqq e)$
(1)f(x)を求めよ。
(2)f(x)の最大値、最小値を求めよ。
この動画を見る
1⃣ $f(x)=\int_1^e |logt-logx|dt (1 \leqq x \leqq e)$
(1)f(x)を求めよ。
(2)f(x)の最大値、最小値を求めよ。
17愛知県教員採用試験(数学:1-1番 整数問題)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣(1)
$\sqrt{n^2+16}$が自然数となるような自然数nを求めよ。
この動画を見る
1⃣(1)
$\sqrt{n^2+16}$が自然数となるような自然数nを求めよ。
