 数と式
数と式
 数と式
数と式
因数分解 大学入試だけど中学生の知識で解ける!福島大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^4+x^2+1+2xy-y^2$
福島大学
この動画を見る
因数分解せよ
$x^4+x^2+1+2xy-y^2$
福島大学
解けるように作られた方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,y,zを実数とするとき,これを解け.
$x+y+z=2(\sqrt x +\sqrt{y-1}+\sqrt{z-2})$
中国中等学校過去問
この動画を見る
x,y,zを実数とするとき,これを解け.
$x+y+z=2(\sqrt x +\sqrt{y-1}+\sqrt{z-2})$
中国中等学校過去問
3乗根の方程式
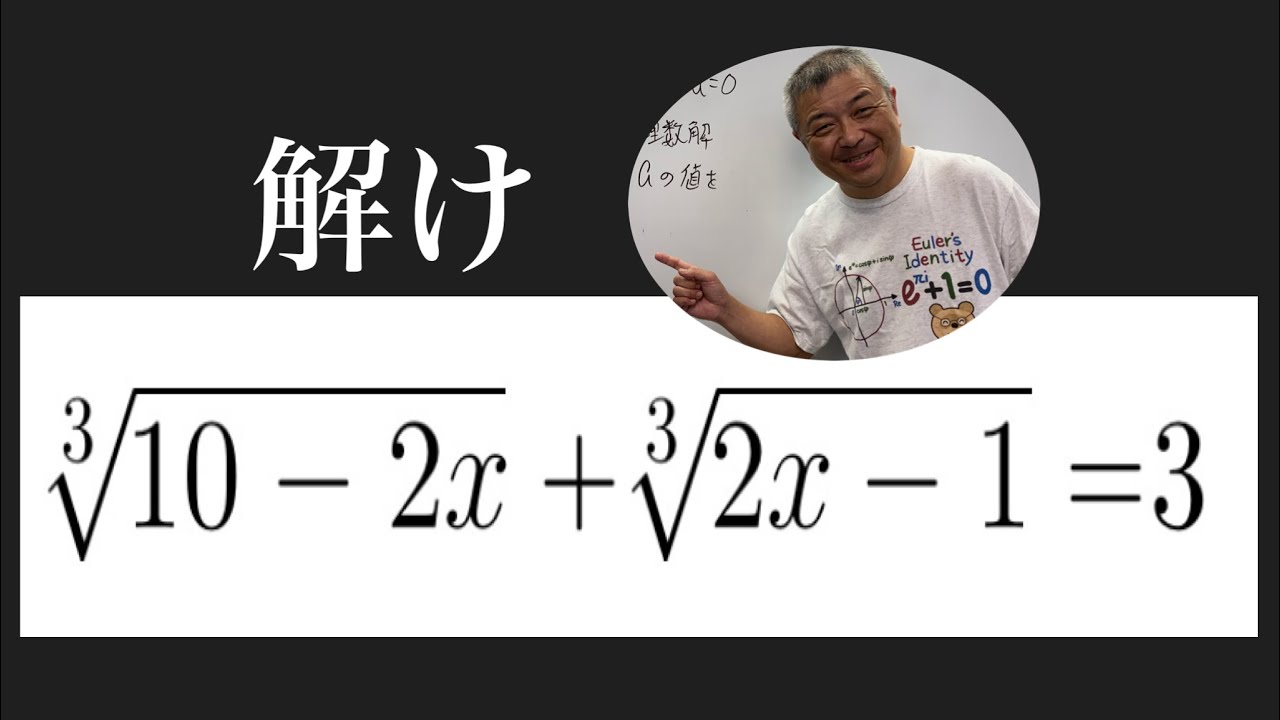
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[3]{10-2x}+\sqrt[3]{2x-1}=3$
これを解け.
この動画を見る
$ \sqrt[3]{10-2x}+\sqrt[3]{2x-1}=3$
これを解け.
ただの計算
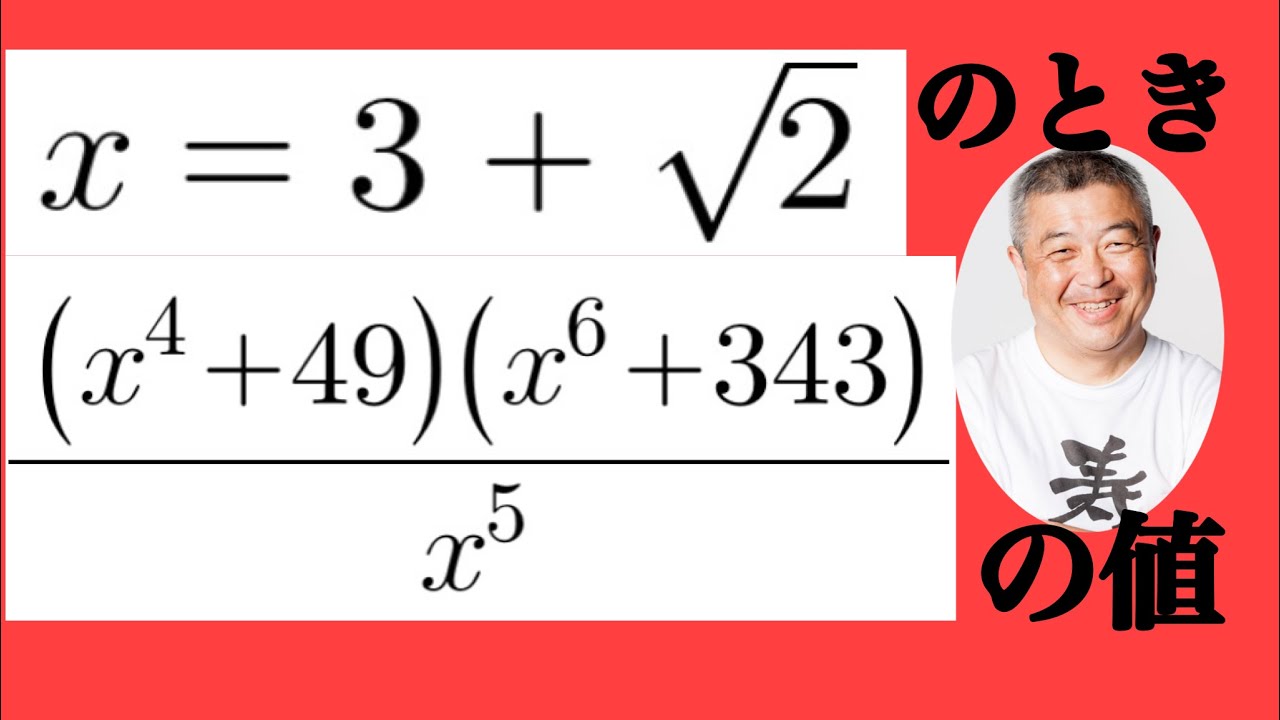
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x=3+\sqrt2,\dfrac{(x^4+49)(x^6+343)}{x^5}$の値を求めよ.
この動画を見る
$ x=3+\sqrt2,\dfrac{(x^4+49)(x^6+343)}{x^5}$の値を求めよ.
3通りで解ける!因数分解 早稲田本庄

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2+b^2-3c^2+2(ab-bc-ca)$を因数分解せよ。
早稲田大学 本庄高等学院
この動画を見る
$a^2+b^2-3c^2+2(ab-bc-ca)$を因数分解せよ。
早稲田大学 本庄高等学院
(x-y)⁵+(y-z)⁵+(z-x)⁵を因数分解せよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x-y)^5+(y-z)^5+(z-x)^5$を因数分解せよ.
この動画を見る
$(x-y)^5+(y-z)^5+(z-x)^5$を因数分解せよ.
解いて代入すれば出るけどね‥‥
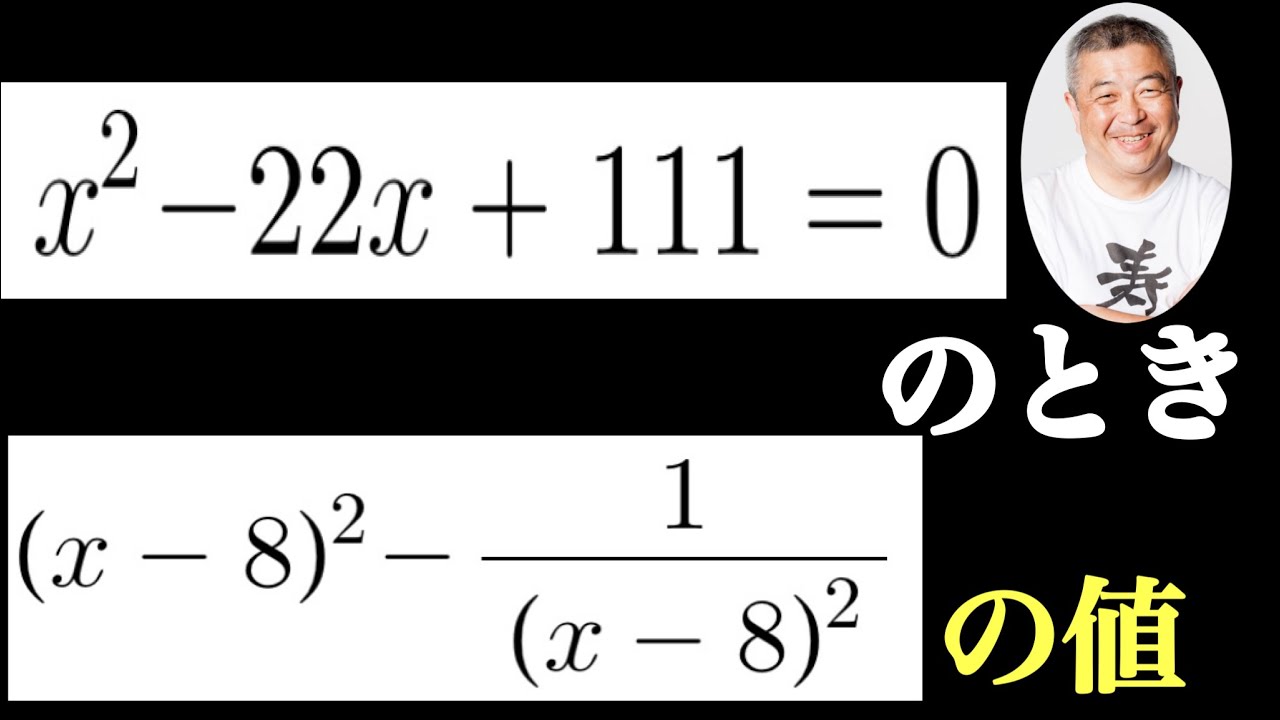
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2-22x+111=0$のとき,
$(x-8)^2-\dfrac{1}{(x-8)^2}$の値を求めよ.
この動画を見る
$ x^2-22x+111=0$のとき,
$(x-8)^2-\dfrac{1}{(x-8)^2}$の値を求めよ.
因数分解!私できませんでした!

二重根号の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{x+6-6\sqrt{x-3}}+\sqrt{x+22-10\sqrt{x-3}}$
$=18$
これを解け.
この動画を見る
$ \sqrt{x+6-6\sqrt{x-3}}+\sqrt{x+22-10\sqrt{x-3}}$
$=18$
これを解け.
2022富山大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left[\sqrt{3\sqrt3+\dfrac{2}{3\sqrt3-1}}\right]$
これを解け.
富山大過去問
この動画を見る
$\left[\sqrt{3\sqrt3+\dfrac{2}{3\sqrt3-1}}\right]$
これを解け.
富山大過去問
√と二乗は打ち消し合う?? 熊本マリスト学園

単元:
#数学(中学生)#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$9+\sqrt {a^2} = 25$
整数aを求めよ
熊本マリスト学園高等学校
この動画を見る
$9+\sqrt {a^2} = 25$
整数aを求めよ
熊本マリスト学園高等学校
連立2元4次方程式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x+y=1 \\
x^4+y^4=881
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x+y=1 \\
x^4+y^4=881
\end{array}
\right.
\end{eqnarray}$
これを解け.
定期試験レベル?平方根の式の値
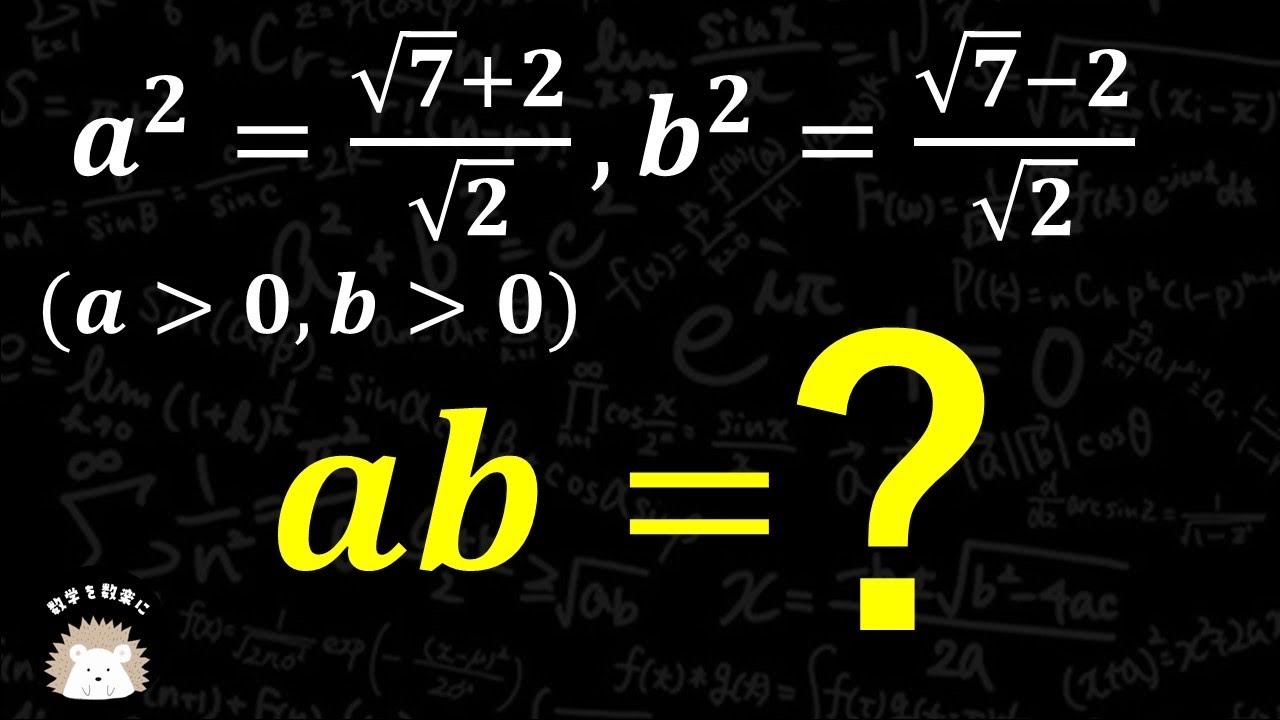
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 = \frac{\sqrt 7 + 2}{\sqrt 2}$ , $b^2 = \frac{\sqrt 7 - 2}{\sqrt 2}$
(a>0 , b>0)
$ab=?$
$a^2b^2=?$
この動画を見る
$a^2 = \frac{\sqrt 7 + 2}{\sqrt 2}$ , $b^2 = \frac{\sqrt 7 - 2}{\sqrt 2}$
(a>0 , b>0)
$ab=?$
$a^2b^2=?$
福田の数学〜上智大学2022年理工学部第1問(1)〜集合と論理

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)x,yを実数とする。次の条件を考える。
$p:xy$が無理数である.
$q:x,y$がともに無理数である.
$r:x,y$の少なくとも一方が無理数である.
$(\textrm{i})$以下から真の命題をすべて選べ。
$(\textrm{a})p \Rightarrow q\ \ \ (\textrm{b})p \Rightarrow r\ \ \ (\textrm{c})q \Rightarrow p\ \ \ (\textrm{d})q \Rightarrow r\ \ \ (\textrm{e})r \Rightarrow p\ \ \ (\textrm{f})r \Rightarrow q\ \ \ \\
(\textrm{ii})x,y$が命題「$p \Rightarrow q$」の判例であるための必要十分条件を、すべて選べ。
$(\textrm{a})$「$xy$が無理数」かつ「x,yが共に有理数」である。
$(\textrm{b})$「$xy$が有理数」かつ「x,yが共に有理数」である。
$(\textrm{c})$「$xy$が有理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{d})$「$xy$が無理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{e})$「$xy$が無理数、かつxが有理数」または「xyが無理数、かつ、yが有
理数」である。
$(\textrm{f})$「$xy$が無理数、かつxが有理数」または「xyが有理数、かつ、yが有
理数」である。
2022上智大学理工学部過去問
この動画を見る
(1)x,yを実数とする。次の条件を考える。
$p:xy$が無理数である.
$q:x,y$がともに無理数である.
$r:x,y$の少なくとも一方が無理数である.
$(\textrm{i})$以下から真の命題をすべて選べ。
$(\textrm{a})p \Rightarrow q\ \ \ (\textrm{b})p \Rightarrow r\ \ \ (\textrm{c})q \Rightarrow p\ \ \ (\textrm{d})q \Rightarrow r\ \ \ (\textrm{e})r \Rightarrow p\ \ \ (\textrm{f})r \Rightarrow q\ \ \ \\
(\textrm{ii})x,y$が命題「$p \Rightarrow q$」の判例であるための必要十分条件を、すべて選べ。
$(\textrm{a})$「$xy$が無理数」かつ「x,yが共に有理数」である。
$(\textrm{b})$「$xy$が有理数」かつ「x,yが共に有理数」である。
$(\textrm{c})$「$xy$が有理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{d})$「$xy$が無理数」かつ「xが有理数、または、yが有理数」である。
$(\textrm{e})$「$xy$が無理数、かつxが有理数」または「xyが無理数、かつ、yが有
理数」である。
$(\textrm{f})$「$xy$が無理数、かつxが有理数」または「xyが有理数、かつ、yが有
理数」である。
2022上智大学理工学部過去問
だからどうした?
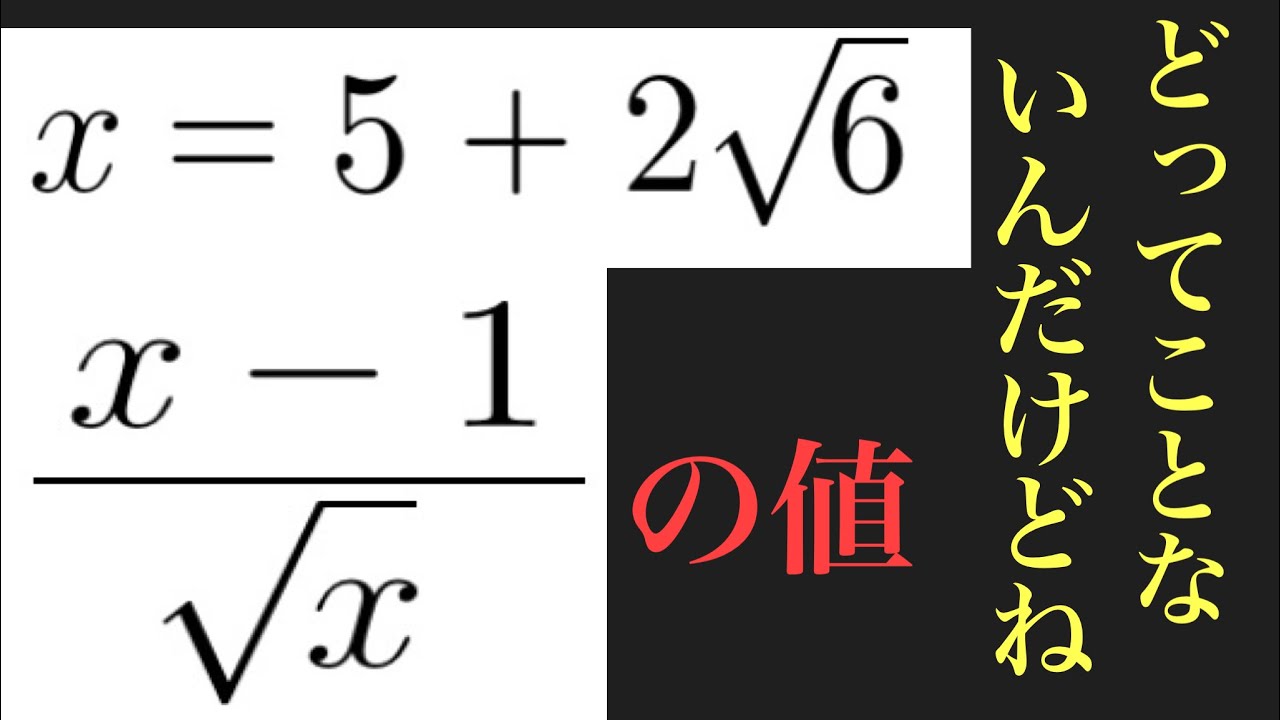
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x=5+2\sqrt6,\dfrac{x-1}{\sqrt x}$
これを解け.
この動画を見る
$ x=5+2\sqrt6,\dfrac{x-1}{\sqrt x}$
これを解け.
方程式
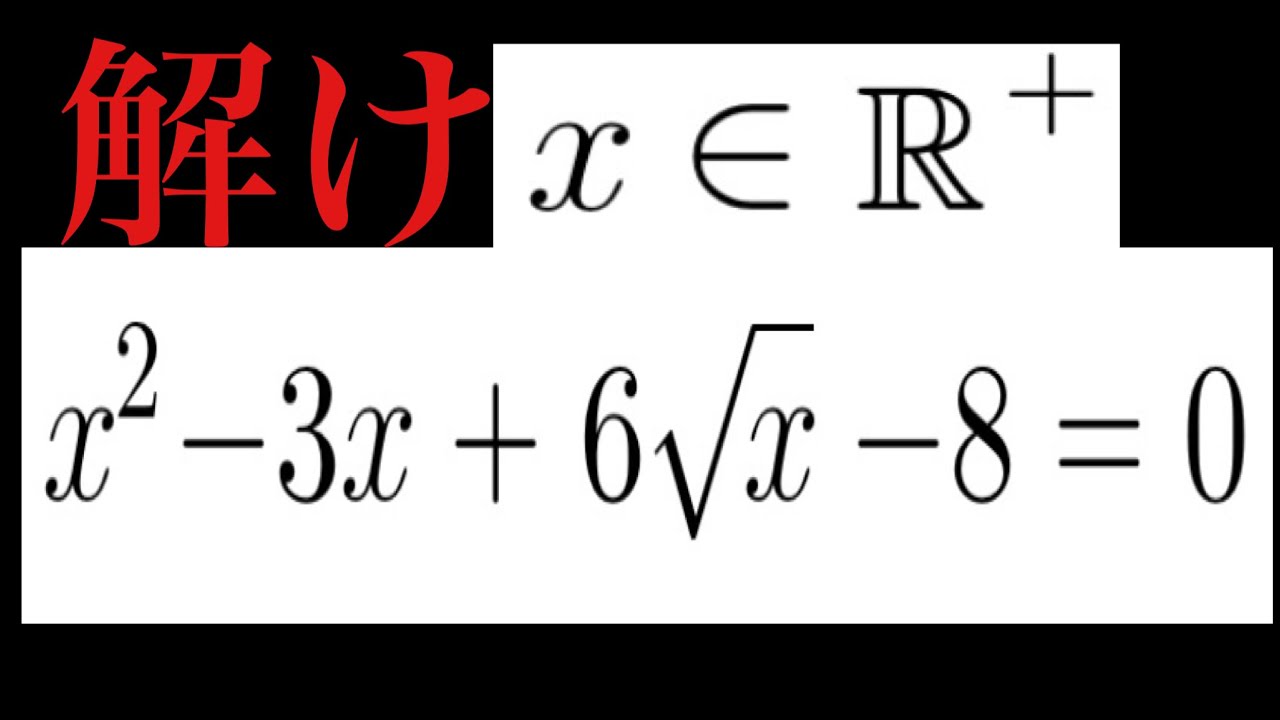
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
xは正の実数であるとする.
$x^2-3x+6\sqrt x-8=0$
これを解け.
この動画を見る
xは正の実数であるとする.
$x^2-3x+6\sqrt x-8=0$
これを解け.
例の問題
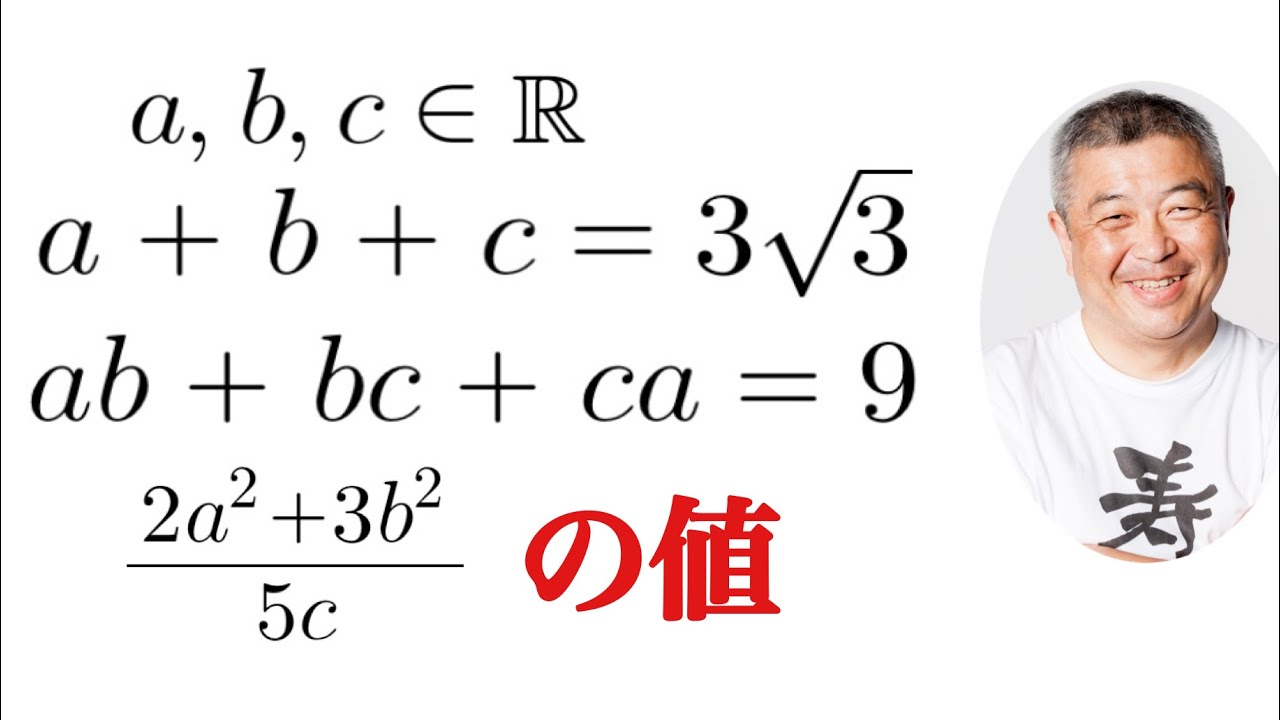
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=3\sqrt3 \\
ab+bc+ca=9
\end{array}
\right.
\end{eqnarray}$
$\dfrac{2a^2+3b^2}{5c}$の値を求めよ.
この動画を見る
a,b,cは実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=3\sqrt3 \\
ab+bc+ca=9
\end{array}
\right.
\end{eqnarray}$
$\dfrac{2a^2+3b^2}{5c}$の値を求めよ.
福田の数学〜上智大学2022年TEAP理系型第1問(3)〜命題と必要十分な条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1
(3) aを正の実数とする。 実数からなる集合X, Yを次で定める。
$X={x|0 < x < a}, Y={y|3 < y < 5}$
次のそれぞれの命題が成り立つための必要十分条件を、選択肢から1つずつ選べ。
(i) すべてのx∈Xとすべてのy∈Yに対してx<yとなる
(ii) 「すべてのx∈Xに対してx<y」となるy∈Yが存在する
(iii) すべてのx∈Xに対して「x<yとなるy∈Yが存在する」
2022上智大学理系過去問
この動画を見る
1
(3) aを正の実数とする。 実数からなる集合X, Yを次で定める。
$X={x|0 < x < a}, Y={y|3 < y < 5}$
次のそれぞれの命題が成り立つための必要十分条件を、選択肢から1つずつ選べ。
(i) すべてのx∈Xとすべてのy∈Yに対してx<yとなる
(ii) 「すべてのx∈Xに対してx<y」となるy∈Yが存在する
(iii) すべてのx∈Xに対して「x<yとなるy∈Yが存在する」
2022上智大学理系過去問
福田の数学〜上智大学2022年TEAP文系型第4問(1)〜必要十分条件と条件の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)実数の数列${a_n}$に関する以下の条件 $(P)$ を考える。
$(P) 「n\geqq N$ならば $a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{i})$ 以下の選択肢から、(P) であるための必要十分条件をすべて選べ。
$(\textrm{ii})$ 以下の選択肢から、(P) であるための必要条件ではあるが十分条件ではないもの
をすべて選べ。
$(\textrm{iii})$ 以下の選択肢から、(P) の否定であるものをすべて選べ。
選択肢$(\textrm{a})$「$n\gt N$ ならば$a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{b})$ 「$n \lt N$ ならば$an \leqq 4$」 が成り立つ自然数Nが存在する
$(\textrm{c})$ 「$n\geqq N$ならば$a_n\gt 4$」 が成り立つ自然数Nが存在する
$(\textrm{d}) a_n \gt 4$ を満たす自然数n が無限個存在する
$(\textrm{e}) a_n \leqq 4$ を満たす自然数nが無限個存在する
$(\textrm{f}) a_n \gt 4$ を満たす自然数nは存在しても有限個である
$(\textrm{g}) a_n \leqq 4$ を満たす自然数nは存在しても有限個である
2022上智大学文系過去問
この動画を見る
(1)実数の数列${a_n}$に関する以下の条件 $(P)$ を考える。
$(P) 「n\geqq N$ならば $a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{i})$ 以下の選択肢から、(P) であるための必要十分条件をすべて選べ。
$(\textrm{ii})$ 以下の選択肢から、(P) であるための必要条件ではあるが十分条件ではないもの
をすべて選べ。
$(\textrm{iii})$ 以下の選択肢から、(P) の否定であるものをすべて選べ。
選択肢$(\textrm{a})$「$n\gt N$ ならば$a_n \leqq 4$」が成り立つ自然数Nが存在する
$(\textrm{b})$ 「$n \lt N$ ならば$an \leqq 4$」 が成り立つ自然数Nが存在する
$(\textrm{c})$ 「$n\geqq N$ならば$a_n\gt 4$」 が成り立つ自然数Nが存在する
$(\textrm{d}) a_n \gt 4$ を満たす自然数n が無限個存在する
$(\textrm{e}) a_n \leqq 4$ を満たす自然数nが無限個存在する
$(\textrm{f}) a_n \gt 4$ を満たす自然数nは存在しても有限個である
$(\textrm{g}) a_n \leqq 4$ を満たす自然数nは存在しても有限個である
2022上智大学文系過去問
【循環小数(じゅんかんしょうすう)とは…!】確率:京都府公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#数と式#確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
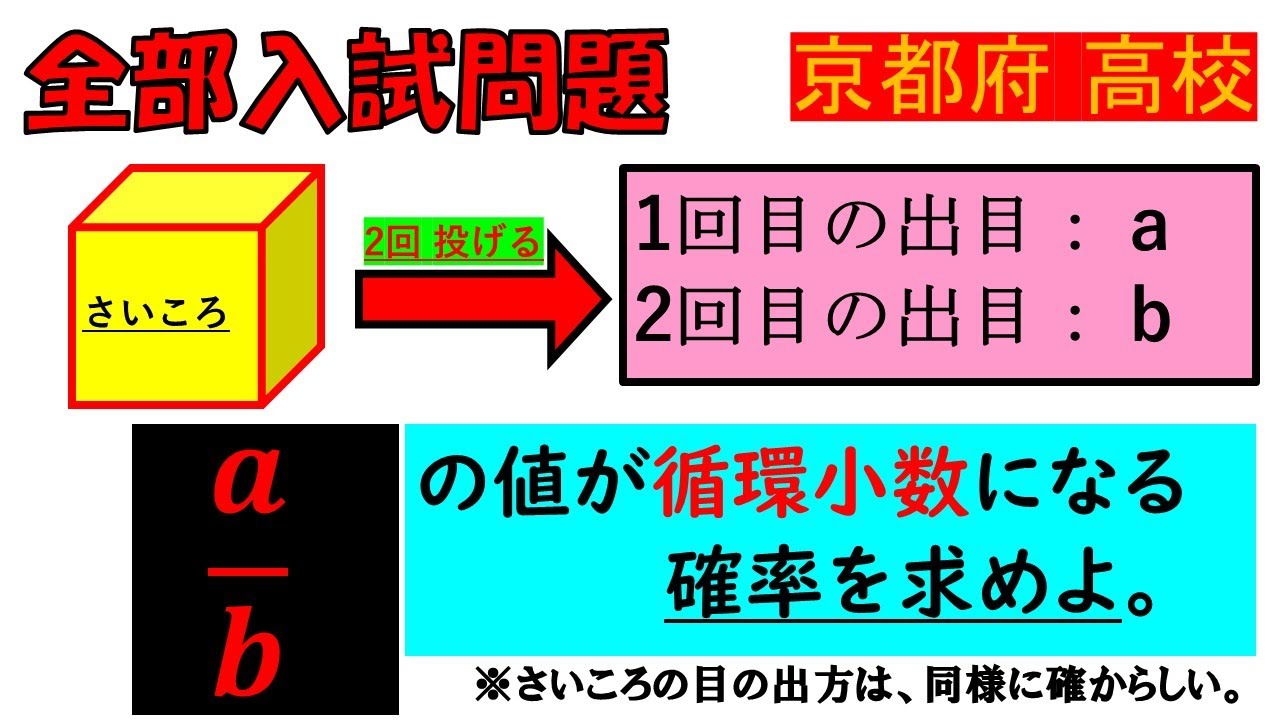
さいころを2回投げた.
1回目の出目は$a$であり,2回目の出目は$b$であった.
$\dfrac{a}{b}$の値が循環小数になる確率を求めよ.
※さいころの目の出方は,同様に確からしい.
京都府高校過去問
この動画を見る
さいころを2回投げた.
1回目の出目は$a$であり,2回目の出目は$b$であった.
$\dfrac{a}{b}$の値が循環小数になる確率を求めよ.
※さいころの目の出方は,同様に確からしい.
京都府高校過去問
指数の計算
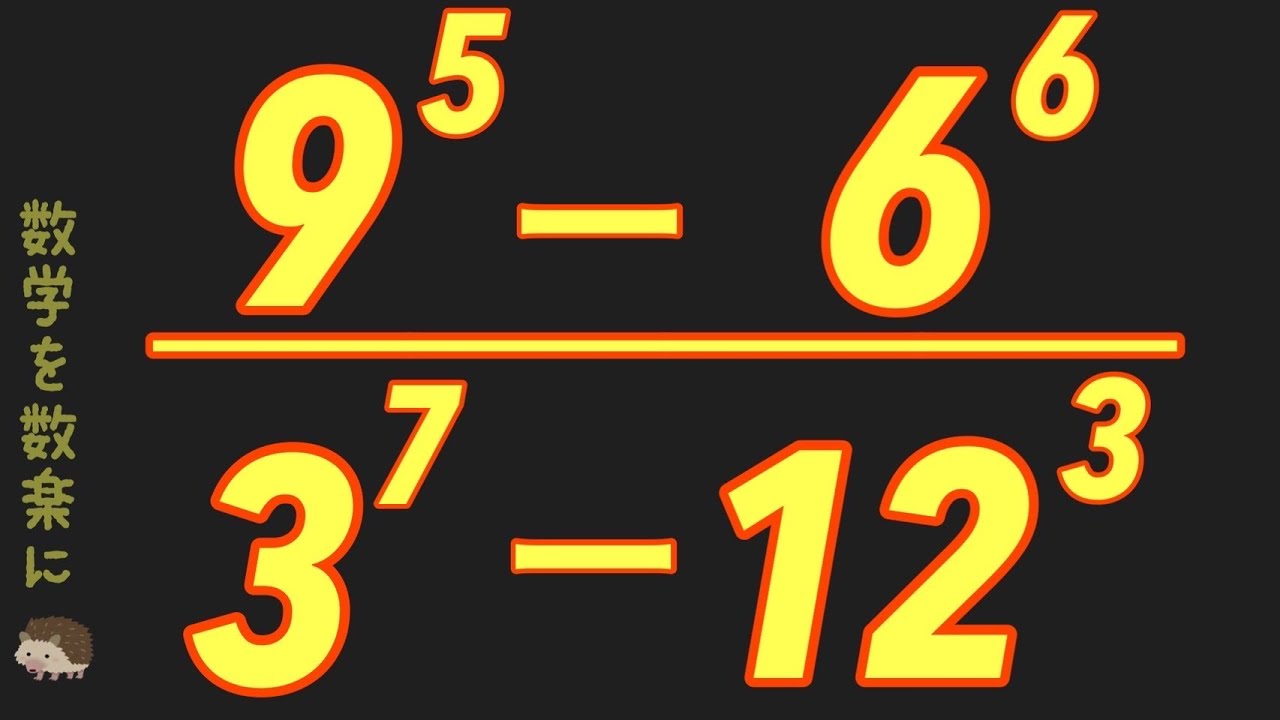
単元:
#数Ⅰ#数Ⅱ#数と式#式の計算(整式・展開・因数分解)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{9^5 -6^6}{3^7 - 12^3}$
この動画を見る
$\frac{9^5 -6^6}{3^7 - 12^3}$
以上未満の覚え方~とんとんと先生の教え方の違い~

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
以上未満の覚え方
この動画を見る
以上未満の覚え方
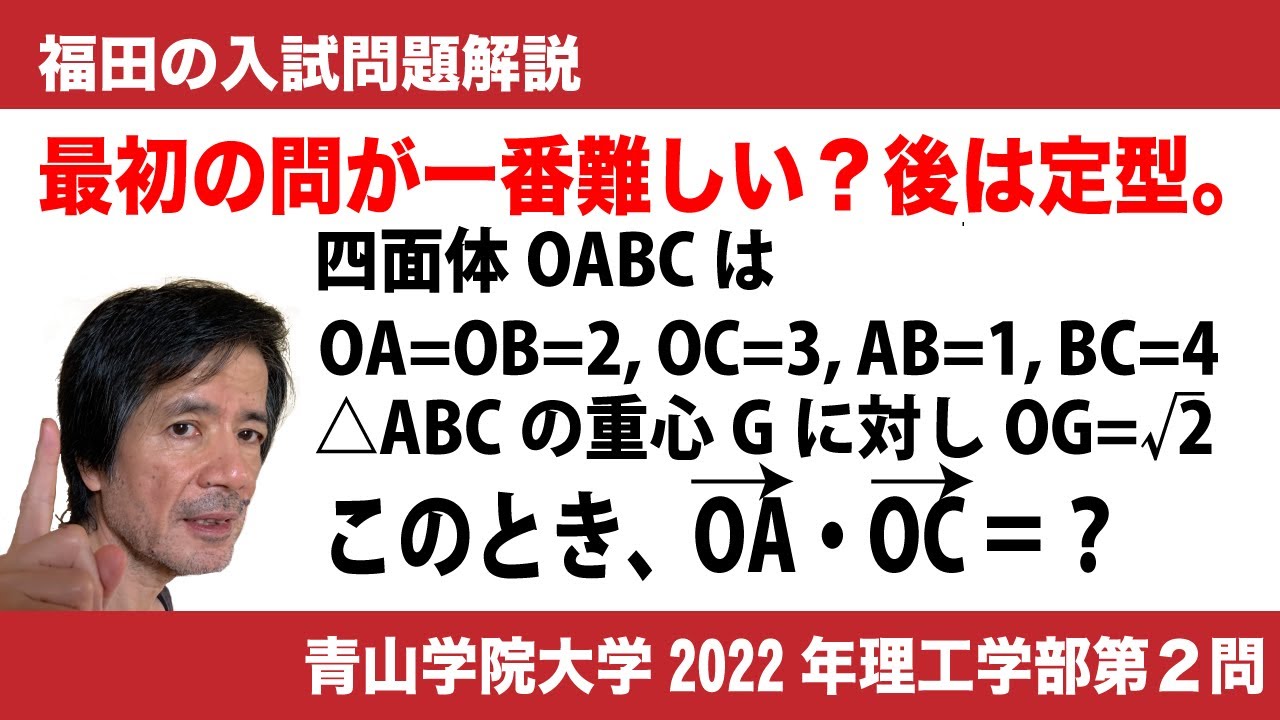
福田の数学〜青山学院大学2022年理工学部第2問〜平面ベクトルの直交と絶対値の最小
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
四面体OABCは
$OA=OB=2,\ \ \ OC=3,\ \ \ AB=1,\ \ \ BC=4$
を満たすとする。また、三角形ABCの重心をGとするとき、$OG=\sqrt2$である。
(1)$\overrightarrow{ OA }・\overrightarrow{ OB }=\frac{\boxed{ア}}{\boxed{イ}},$
$\ \ \ \overrightarrow{ OA }・\overrightarrow{ OC}=\frac{\boxed{ウエ}}{\boxed{オ}}$
(2)$\ \overrightarrow{ OG }$と$\overrightarrow{ OA }+k\overrightarrow{ OB }$が垂直であるのは$k=\boxed{カキ}$のときである。
(3)$t$を実数とする。
$|t\overrightarrow{ OA }-2t\overrightarrow{ OB }+\overrightarrow{ OC }|$
の最小値は$\frac{\sqrt{\boxed{クケコ}}}{\boxed{サ}}$であり、
そのときのtの値は$\frac{\boxed{シス}}{\boxed{セ}}$である。
2022青山学院大学理工学部過去問
この動画を見る
四面体OABCは
$OA=OB=2,\ \ \ OC=3,\ \ \ AB=1,\ \ \ BC=4$
を満たすとする。また、三角形ABCの重心をGとするとき、$OG=\sqrt2$である。
(1)$\overrightarrow{ OA }・\overrightarrow{ OB }=\frac{\boxed{ア}}{\boxed{イ}},$
$\ \ \ \overrightarrow{ OA }・\overrightarrow{ OC}=\frac{\boxed{ウエ}}{\boxed{オ}}$
(2)$\ \overrightarrow{ OG }$と$\overrightarrow{ OA }+k\overrightarrow{ OB }$が垂直であるのは$k=\boxed{カキ}$のときである。
(3)$t$を実数とする。
$|t\overrightarrow{ OA }-2t\overrightarrow{ OB }+\overrightarrow{ OC }|$
の最小値は$\frac{\sqrt{\boxed{クケコ}}}{\boxed{サ}}$であり、
そのときのtの値は$\frac{\boxed{シス}}{\boxed{セ}}$である。
2022青山学院大学理工学部過去問
ルートを含む方程式

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$\sqrt{2x-1} - \sqrt {x-1} = \sqrt {6-x}$
岡山県立大学
この動画を見る
方程式を解け
$\sqrt{2x-1} - \sqrt {x-1} = \sqrt {6-x}$
岡山県立大学
中学生も解ける??因数分解 福島大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^4+x^2+1+2xy-y^2$
福島大学
この動画を見る
因数分解せよ
$x^4+x^2+1+2xy-y^2$
福島大学
福田の数学〜立教大学2022年経済学部第1問(2)〜絶対の付いた方程式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
この動画を見る
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
二重根号を外せ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{4.5+\sqrt2+2\sqrt3+\sqrt6}$
これの二重根号を外せ.
この動画を見る
$ \sqrt{4.5+\sqrt2+2\sqrt3+\sqrt6}$
これの二重根号を外せ.
一度はみんな間違える変域 国分寺高校
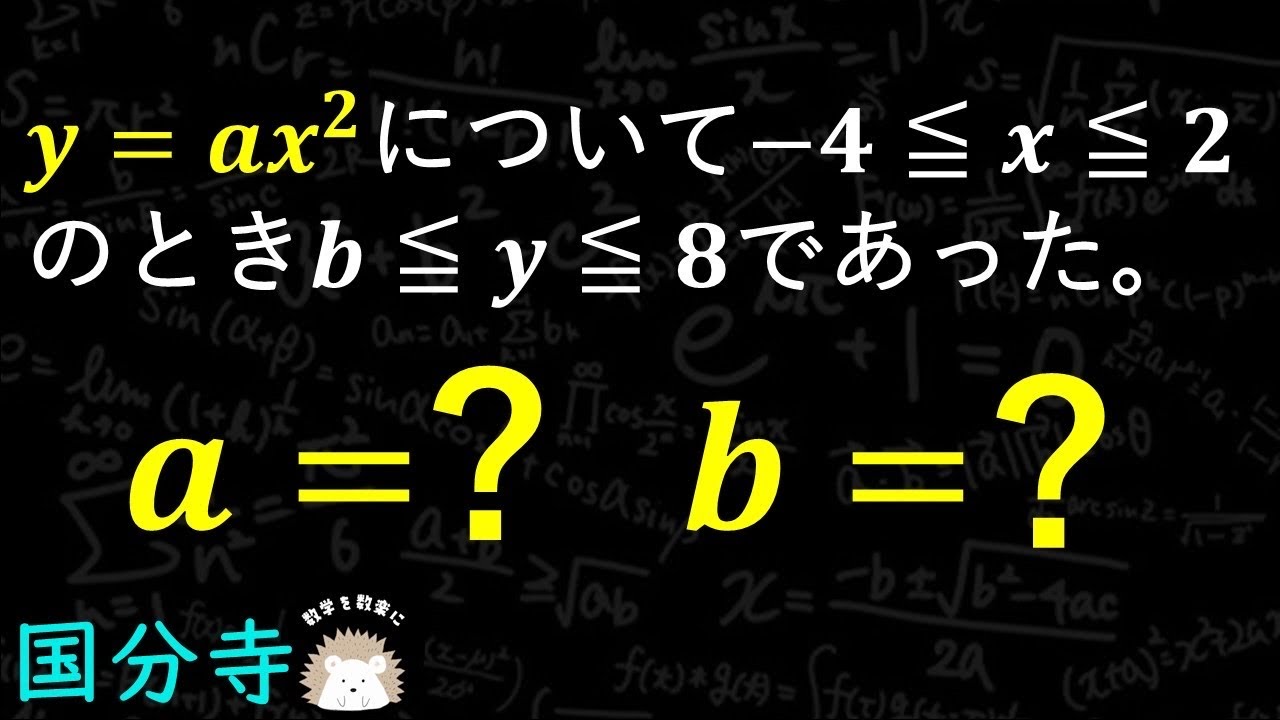
単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=ax^2$について$-4 \leqq x \leqq 2$のとき$b \leqq y \leqq 8$であった。
a=? b=?
国分寺高等学校
この動画を見る
$y=ax^2$について$-4 \leqq x \leqq 2$のとき$b \leqq y \leqq 8$であった。
a=? b=?
国分寺高等学校
因数分解せよ 北京大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x \sqrt x - 2x + 1$
北京大学
この動画を見る
因数分解せよ
$x \sqrt x - 2x + 1$
北京大学
和と差の積は? 灘高校

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(c-a)^2+3b^2 = 4b\\
(a-b)^2+3c^2 = 4c\\
b \neq c
\end{array}
\right.
\end{eqnarray}
$
aをb,cの1次式で表せ。
灘高等学校
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(c-a)^2+3b^2 = 4b\\
(a-b)^2+3c^2 = 4c\\
b \neq c
\end{array}
\right.
\end{eqnarray}
$
aをb,cの1次式で表せ。
灘高等学校
