 2次関数
2次関数
 2次関数
2次関数
2次不等式はこの手順通りに考えれば解けちゃう!? #数学 #高校数学 #不等式
【高校数学】2次不等式はこれでマスター!この手順通りに考えれば解けちゃう【数学のコツ】
ルートの方程式 むりっすぅ
複雑な2次方程式。あれ使え。桐光学園

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$2(x-1)^2-4\sqrt3(x-1)+1=0$
2024桐光学園高等学校
この動画を見る
方程式を解け
$2(x-1)^2-4\sqrt3(x-1)+1=0$
2024桐光学園高等学校
福田の数学〜早稲田大学2024年人間科学部第1問(2)〜不等式の表す領域の面積

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
この動画を見る
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
一手間加えるだけで美味しい方程式

【その手があったか…!】:因数分解への応用(その5)~中学からの二次方程式

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式の解の公式を用いて
$ px^2+(2p-1)x-(4p-1)$を因数分解せよ.
ただし,$ p\neq 0$とする.
この動画を見る
2次方程式の解の公式を用いて
$ px^2+(2p-1)x-(4p-1)$を因数分解せよ.
ただし,$ p\neq 0$とする.
福田のおもしろ数学096〜連立方程式が実数解をもつ条件

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$,$b$が実数のとき、次の連立方程式が実数解をもつための$a$,$b$の条件を求めよ。
$\left\{\begin{array}{1}
x+y+z=a ...①
x^2+y^2+z^2=b ...②
\end{array}\right.$
この動画を見る
$a$,$b$が実数のとき、次の連立方程式が実数解をもつための$a$,$b$の条件を求めよ。
$\left\{\begin{array}{1}
x+y+z=a ...①
x^2+y^2+z^2=b ...②
\end{array}\right.$
二次関数と変域 2024明大中野

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=\frac{1}{3}x^2$について、xの変域が$a-6 \leqq x \leqq a$のとき、yの変域は$0 \leqq y \leqq 9$となる。
aの値をすべて求めよ。
2024明治大学付属中野高等学校
この動画を見る
$y=\frac{1}{3}x^2$について、xの変域が$a-6 \leqq x \leqq a$のとき、yの変域は$0 \leqq y \leqq 9$となる。
aの値をすべて求めよ。
2024明治大学付属中野高等学校
2次方程式 3通りで解説!! 2024日比谷高校

単元:
#数Ⅰ#大学入試過去問(数学)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$(x-1)^2-4(x-2)^2=0$
2024日比谷高等学校
この動画を見る
方程式を解け
$(x-1)^2-4(x-2)^2=0$
2024日比谷高等学校
福田のおもしろ数学085〜不等式を満たす自然数の組合せ

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$<$b$<$c$を満たす正の整数の組($a$,$b$,$c$)であって、
$a^2$-$20005a$>$b^2$-$20005b$>$c^2$-$20005c$
が成り立つものはいくつあるか。
この動画を見る
$a$<$b$<$c$を満たす正の整数の組($a$,$b$,$c$)であって、
$a^2$-$20005a$>$b^2$-$20005b$>$c^2$-$20005c$
が成り立つものはいくつあるか。
意外と間違える!?二次方程式 2024京都府

単元:
#数Ⅰ#大学入試過去問(数学)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$8x^2=22x$
2024京都府
この動画を見る
方程式を解け
$8x^2=22x$
2024京都府
知っていれば一瞬!!2次方程式と解と式の関係 2024早稲田実業

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$3x^2-4x-2=0$の2つの解をa,bとする。
$(3a^2-4a+2)(6b^2-8b)=?$
2024早稲田実業学校
この動画を見る
$3x^2-4x-2=0$の2つの解をa,bとする。
$(3a^2-4a+2)(6b^2-8b)=?$
2024早稲田実業学校
二次方程式の解が1つ 灘高校2024

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xの二次方程式
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値をすべて求めよ
灘高等学校2024
この動画を見る
xの二次方程式
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値をすべて求めよ
灘高等学校2024
ルートを含む二次方程式の計算 2024早稲田本庄最初の一問

単元:
#数Ⅰ#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 5 + \sqrt 3 )x^2+2 \sqrt 3x - \sqrt 5+ \sqrt 3= 0$を解け
2024早稲田大学 本庄高等学院
この動画を見る
$(\sqrt 5 + \sqrt 3 )x^2+2 \sqrt 3x - \sqrt 5+ \sqrt 3= 0$を解け
2024早稲田大学 本庄高等学院
二次方程式の解と確率 2024立教新座

単元:
#数Ⅰ#数A#2次関数#場合の数と確率#2次方程式と2次不等式#確率#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
さいころを3回続けて投げるとき、1回目、2回目、3回目に出た目の数をそれぞれa,b,cとする。
2次方程式$ax^2+bx+c=0$について2つの解が-2、-3となる確率を求めよ
2024立教新座高等学校
この動画を見る
さいころを3回続けて投げるとき、1回目、2回目、3回目に出た目の数をそれぞれa,b,cとする。
2次方程式$ax^2+bx+c=0$について2つの解が-2、-3となる確率を求めよ
2024立教新座高等学校
福田のおもしろ数学037〜相加相乗平均の罠〜2変数関数の最小値

単元:
#数Ⅰ#2次関数#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
この動画を見る
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
2024年共通テスト徹底解説〜数学ⅠA第2問(1)2次関数〜福田の入試問題解説

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
2024年の2次方程式
ちょっと変わった2次方程式
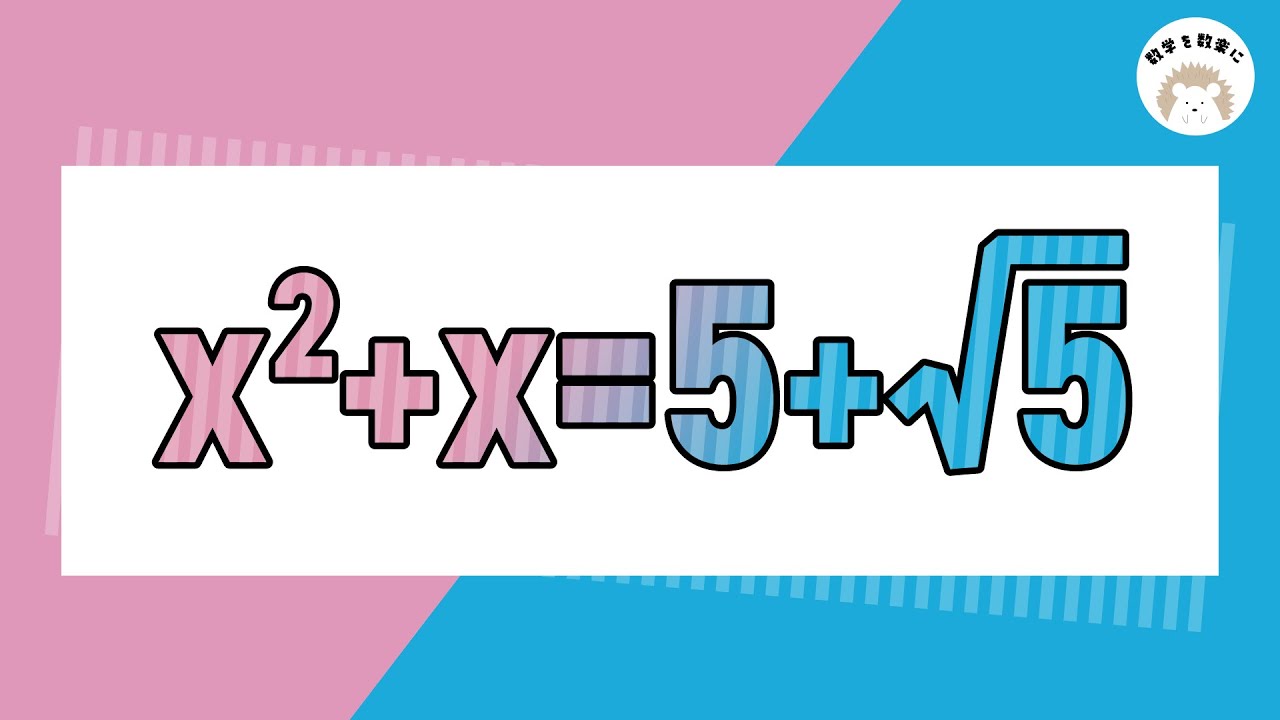
君はどうやって解く? 3通りで解説 二次方程式の計算 八王子東

二次方程式の解が2つの整数 戸山

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xの2次方程式$x^2+ax-8=0$の2つの解がともに整数であるとき、aの値をすべて求めよ。
戸山高等学校
この動画を見る
xの2次方程式$x^2+ax-8=0$の2つの解がともに整数であるとき、aの値をすべて求めよ。
戸山高等学校
福田の数学〜長文問題を解くコツは〜慶應義塾大学2023年環境情報学部第6問〜長文問題と2次関数

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{6}$いま、 A 国の部品会社 A 社から B 国のメ ー カ ー B 社が一定量の部品の取引を行うために、その取引価格pを交渉している。 A 社の生産コスト c は事前の投資額xに依存し、$\dfrac{1}{8}x^2-10x+220$が成り立っているものとすると、 A 社の利益はp-c-xと表すことができる。一方、 B 社はこの部品を使用し生産を行うことで308 の売上を得ることができるものとすると、 A 社から部品を輸人する際に 10 %の関税が課せられるため、 B 社の利益は$308- \dfrac{11}{10}p$と表すことができる。ところで、交渉は常に成立するわけではなく決裂することもあるから、 A 社およびB 社は共に決裂した場合のことを考慮しながら互いに交渉しなければならないそこで、交渉が成立したときの A 社 (B 社)の利益から、交渉が決裂したときのA社(B社)の利益(負の場合は損失を意味する)を引いた値を、A社(B社)の純利益と呼び、 A 社の純利益と B 社の純利益の積を最大化するようにpの値が定まるものとする。またA社は以上のことを踏まえて、自らの利益p-c-xを最大化するようなxの大きさの投資を、事前に行っておくものとする。
(1)交渉が決裂した時、A社は生産を行わず生産コストはかからないが、事前の投資額xの分だけ損失を被るのでA社の利益は-xとなり、B社はB国内の他の部品会社から、価格220で同僚の同じ部品を調達できるとすると、(この場合は関税がかからないことから)B社の利益は308-220=88となる。この場合の投資額xは$\fbox{ア}$となり、価格pは$\fbox{イ}$となる。
(2)交渉が決裂した時、A者は国内の他のメーカーに価格250で部品を販売できるとするとB社の利益は0となる。この場合の投資額xは$\fbox{ウ}$となり、価格pは$\fbox{エ}$となる。
最後に、交渉が成立した場合の「(2)の会社の利益」ー「(1)のA社の利益」=$\fbox{オ}$
2023慶應義塾大学環境情報学部過去問
この動画を見る
$\fbox{6}$いま、 A 国の部品会社 A 社から B 国のメ ー カ ー B 社が一定量の部品の取引を行うために、その取引価格pを交渉している。 A 社の生産コスト c は事前の投資額xに依存し、$\dfrac{1}{8}x^2-10x+220$が成り立っているものとすると、 A 社の利益はp-c-xと表すことができる。一方、 B 社はこの部品を使用し生産を行うことで308 の売上を得ることができるものとすると、 A 社から部品を輸人する際に 10 %の関税が課せられるため、 B 社の利益は$308- \dfrac{11}{10}p$と表すことができる。ところで、交渉は常に成立するわけではなく決裂することもあるから、 A 社およびB 社は共に決裂した場合のことを考慮しながら互いに交渉しなければならないそこで、交渉が成立したときの A 社 (B 社)の利益から、交渉が決裂したときのA社(B社)の利益(負の場合は損失を意味する)を引いた値を、A社(B社)の純利益と呼び、 A 社の純利益と B 社の純利益の積を最大化するようにpの値が定まるものとする。またA社は以上のことを踏まえて、自らの利益p-c-xを最大化するようなxの大きさの投資を、事前に行っておくものとする。
(1)交渉が決裂した時、A社は生産を行わず生産コストはかからないが、事前の投資額xの分だけ損失を被るのでA社の利益は-xとなり、B社はB国内の他の部品会社から、価格220で同僚の同じ部品を調達できるとすると、(この場合は関税がかからないことから)B社の利益は308-220=88となる。この場合の投資額xは$\fbox{ア}$となり、価格pは$\fbox{イ}$となる。
(2)交渉が決裂した時、A者は国内の他のメーカーに価格250で部品を販売できるとするとB社の利益は0となる。この場合の投資額xは$\fbox{ウ}$となり、価格pは$\fbox{エ}$となる。
最後に、交渉が成立した場合の「(2)の会社の利益」ー「(1)のA社の利益」=$\fbox{オ}$
2023慶應義塾大学環境情報学部過去問
4次関数の最小値

4次方程式

ガウス記号!これは取りたい!【早稲田大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の等式を満たす最大の整数aは、a=?である。
[$\displaystyle \frac{a}{2}$]+[$\displaystyle \frac{2a}{3}$]=a
但し、実数xに対して、$\lbrack x \rbrack$は、x以下の最大の整数を表す。
早稲田大過去問
この動画を見る
次の等式を満たす最大の整数aは、a=?である。
[$\displaystyle \frac{a}{2}$]+[$\displaystyle \frac{2a}{3}$]=a
但し、実数xに対して、$\lbrack x \rbrack$は、x以下の最大の整数を表す。
早稲田大過去問
共テ数学90%取る勉強法

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#式と証明#複素数と方程式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#指数関数#対数関数#平均変化率・極限・導関数#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト数学90%取る勉強法説明動画です
この動画を見る
共通テスト数学90%取る勉強法説明動画です
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜虚数係数の2次方程式の解き方〜明治大学2023年全学部統一ⅠⅡAB第1問(2)〜

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(2)$k$を実数とする。$x$についての方程式
$x^2$-(4-3$i$)$x$+(4-$ki$)=0
を満たす実数$x$があるとき、$k$=$\boxed{\ \ キ\ \ }$である。このとき、上の等式を満たす$x$の値は2つあり、$\boxed{\ \ ク\ \ }$と$\boxed{\ \ ケ\ \ }$-$\boxed{\ \ コ\ \ }$$i$ である。ただし、$i$を虚数単位とする。
この動画を見る
$\Large{\boxed{1}}$
(2)$k$を実数とする。$x$についての方程式
$x^2$-(4-3$i$)$x$+(4-$ki$)=0
を満たす実数$x$があるとき、$k$=$\boxed{\ \ キ\ \ }$である。このとき、上の等式を満たす$x$の値は2つあり、$\boxed{\ \ ク\ \ }$と$\boxed{\ \ ケ\ \ }$-$\boxed{\ \ コ\ \ }$$i$ である。ただし、$i$を虚数単位とする。
引くばか 二次方程式の応用 昭和学院秀英

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$2x^2-5x+c=0$の2つの解の比が2:3である。
定数cの値を求めよ。
昭和学院秀英高等学校
この動画を見る
2次方程式$2x^2-5x+c=0$の2つの解の比が2:3である。
定数cの値を求めよ。
昭和学院秀英高等学校
