 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
2023高校入試解説32問目 3辺の長さがわかれば面積求まる 桃山学院

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
2023桃山学院高等学校
この動画を見る
△ABC=?
*図は動画内参照
2023桃山学院高等学校
全体の面積を求めよ

【短時間でマスター!!】内接円や外接円と三角形に関する面積の求め方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
内接円や外接円と三角形に関する面積の求め方を解説します。
この動画を見る
数学1A
内接円や外接円と三角形に関する面積の求め方を解説します。
福田の1.5倍速演習〜合格する重要問題093〜中央大学2020年度理工学部第5問〜円周上の点と三角形五角形の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#微分法と積分法#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa >0,b >0, a +b<$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0<a<$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。
2020中央大学理工学部過去問
この動画を見る
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa >0,b >0, a +b<$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0<a<$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。
2020中央大学理工学部過去問
【短時間でマスター!!】三角形の面積の求め方を解説!〔現役塾講師解説、数学〕

【短時間でマスター!!】正弦定理・余弦定理を解説!〔現役塾講師解説、数学〕

ハルハルさんの作成問題「たぶん名作だと思います。難易度は高め」 図形 三角比

単元:
#数Ⅰ#数Ⅱ#式と証明#図形と計量#三角比への応用(正弦・余弦・面積)#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
この動画を見る
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
補助線のセンスを磨け!2通りで解説

高さが等しい面積比

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
高さが等しい図形の面積比
A:B:C=
*図は動画内参照
この動画を見る
高さが等しい図形の面積比
A:B:C=
*図は動画内参照
【高校数学】余弦定理の応用~問題演習~ 3-7.5【数学Ⅰ】

【数検2級】数学検定2級2次:問題6
単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学検定#数学検定2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
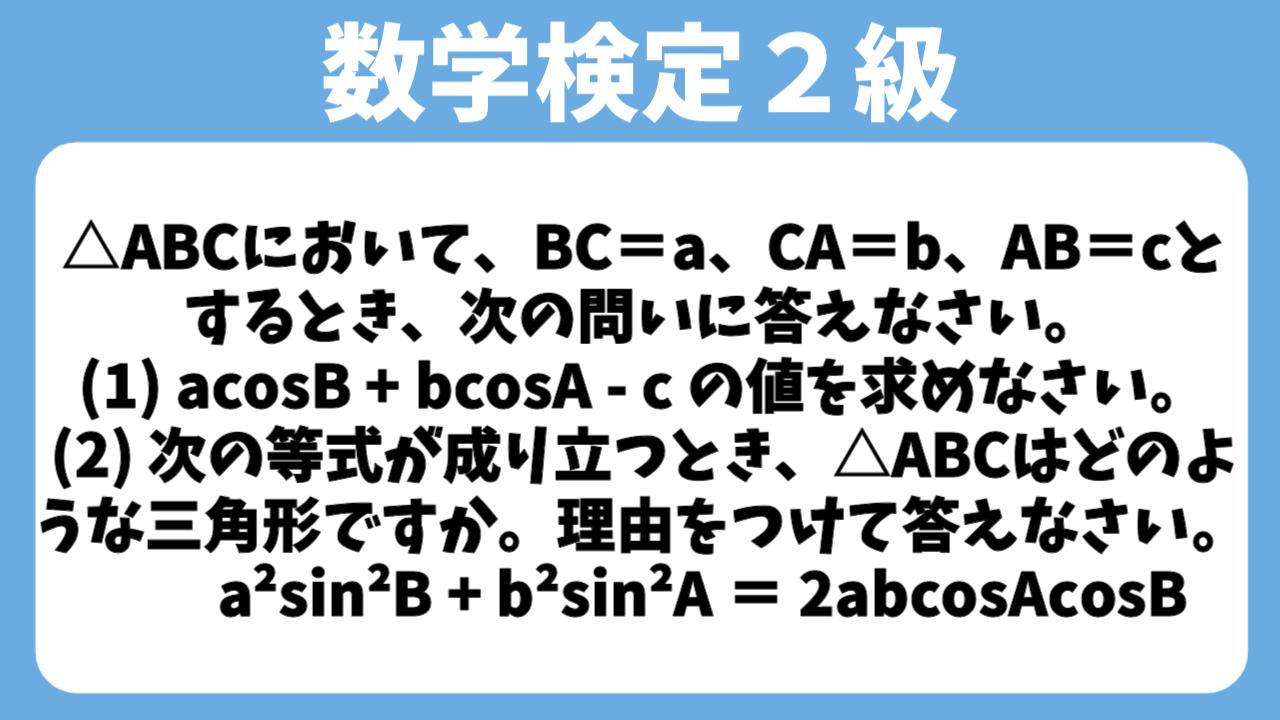
問題6.(必須)
△ABCにおいて、$BC=a、CA=b、AB=c$とするとき、次の問いに答えなさい。
(1)$a\cos B+b\cos A-c$ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 次の等式が成り立つとき、△ABCはどのような三角形ですか。理由をつけて答えなさい。
$a^2\sin^2B+b^2\sin^2 A=2ab\cos A\cos B$
この動画を見る
問題6.(必須)
△ABCにおいて、$BC=a、CA=b、AB=c$とするとき、次の問いに答えなさい。
(1)$a\cos B+b\cos A-c$ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 次の等式が成り立つとき、△ABCはどのような三角形ですか。理由をつけて答えなさい。
$a^2\sin^2B+b^2\sin^2 A=2ab\cos A\cos B$
角の和 茨城県 動画内に誘導あり 茨城県
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
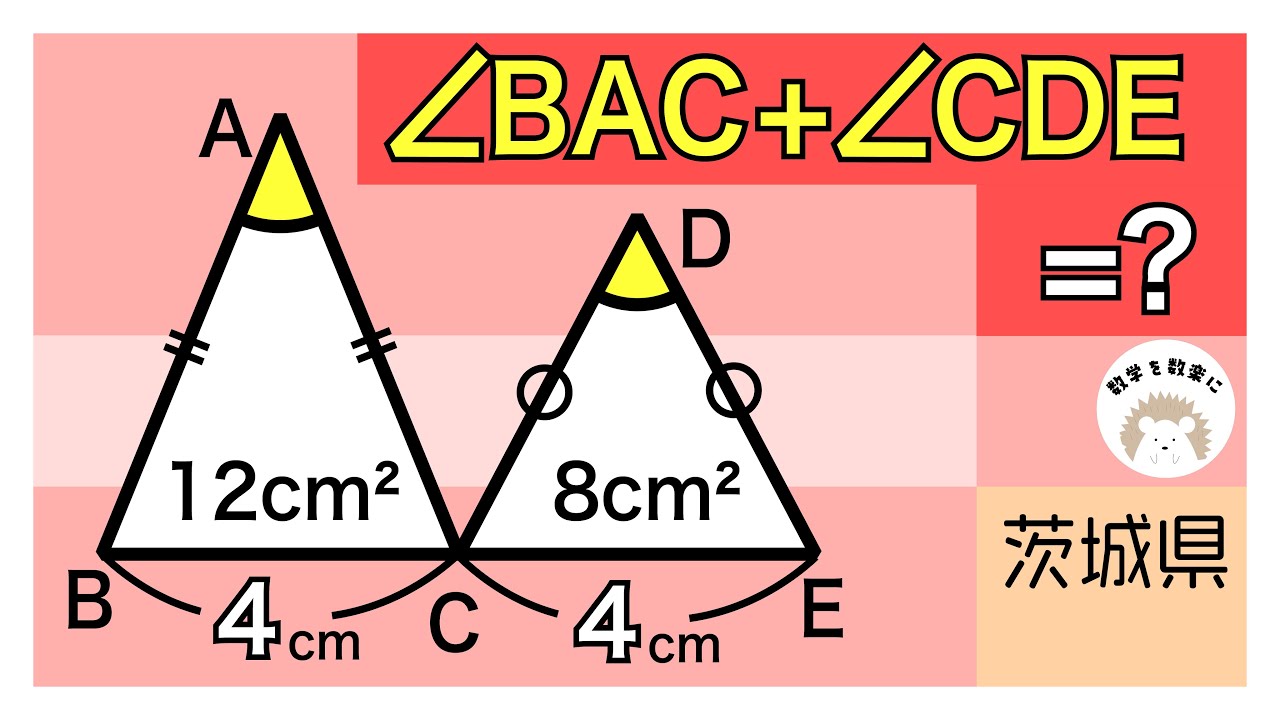
$\angle BAC + \angle CDE$=?
*図は動画内参照
茨城県
この動画を見る
$\angle BAC + \angle CDE$=?
*図は動画内参照
茨城県
福田の数学〜上智大学2022年理工学部第2問〜三角比と通過領域の体積
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
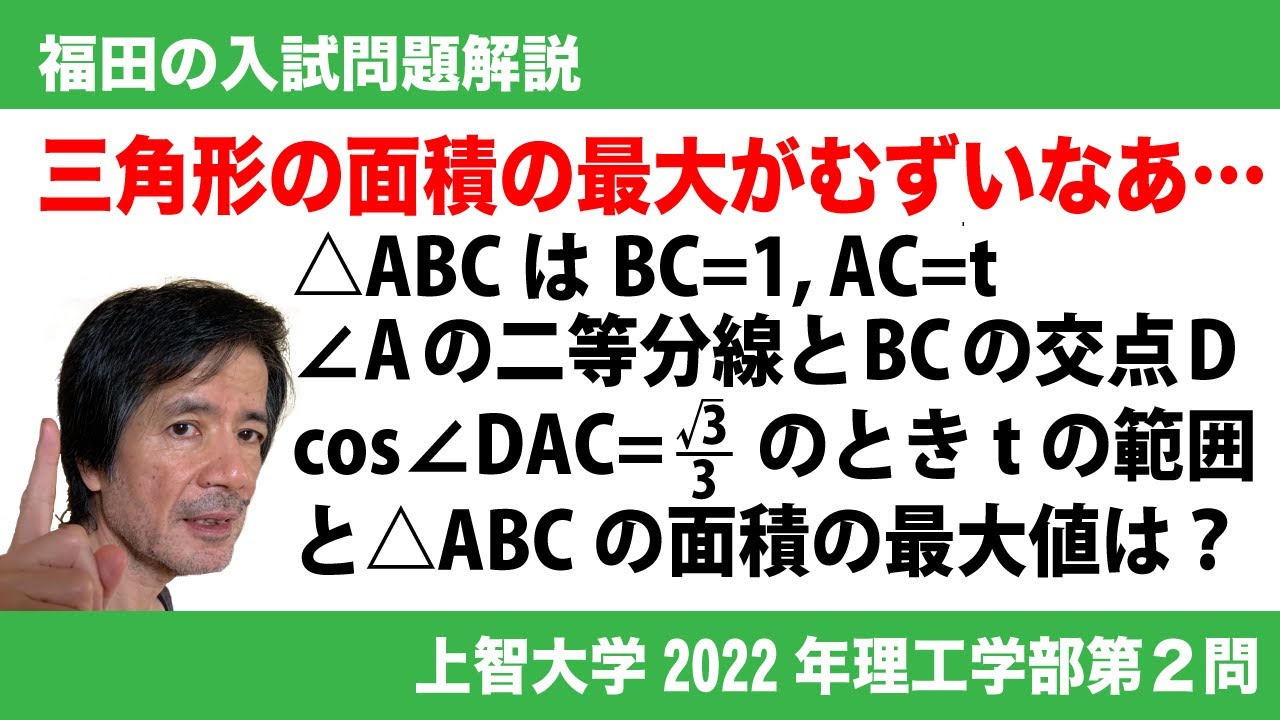
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
この動画を見る
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
正方形と2つの正三角形の面積の和 2通りで解説
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
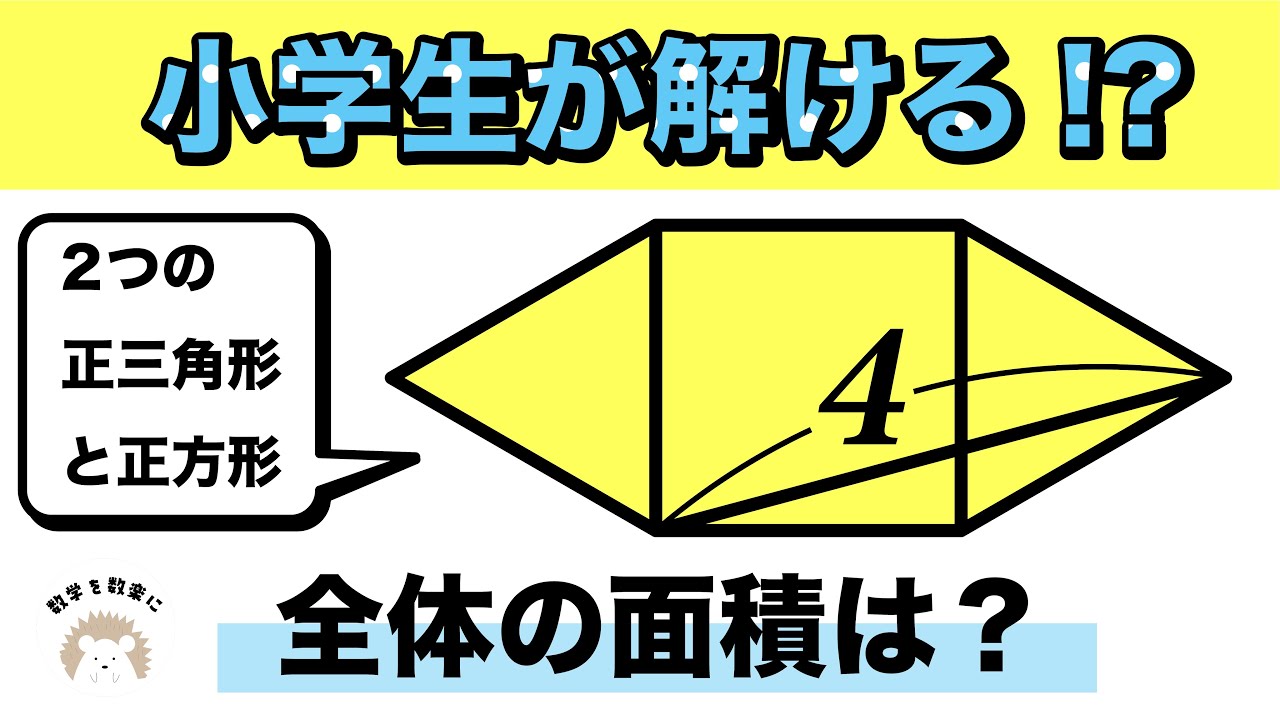
2つの正三角形と正方形
全体の面積=?
*図は動画内参照
この動画を見る
2つの正三角形と正方形
全体の面積=?
*図は動画内参照
【中学からの!】余弦定理(2):三角比~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において
$ a \cos A=b \cos B$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において
$ a \cos A=b \cos B$ならばどんな三角形か.
福田の数学〜明治大学2022年理工学部第2問〜平面図形の計量

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#英語(高校生)#平面図形#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#明治大学#数学(高校生)#明治大学
指導講師:
福田次郎
問題文全文(内容文):
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
この動画を見る
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
【中学からの!】余弦定理(1):三角比~全国入試問題解法
単元:
#数学(中学生)#図形と計量#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において
$ a \cos B=b \cos A$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において
$ a \cos B=b \cos A$ならばどんな三角形か.
福田の数学〜明治大学2022年全学部統一入試12AB第1問(4)〜角の二等分線と辺の長さの軽量

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
この動画を見る
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
【中学から分かる!】正弦定理(2):三角比 特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において,$a \sin A=b \sin B=c \sin C$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において,$a \sin A=b \sin B=c \sin C$ならばどんな三角形か.
【中学から学ぶ!】正弦定理(1):三角比 特別講義~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \triangle ABC$において$ \sin^2 A=\sin^2 B+\sin^2 C$ならばどんな三角形か.
この動画を見る
$ \triangle ABC$において$ \sin^2 A=\sin^2 B+\sin^2 C$ならばどんな三角形か.
福田の数学〜早稲田大学2022年人間科学部第1問(3)〜三角形の辺の関係から角の関係を求める

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
【ここからでも楽しめる!】三角比の計算(4):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
この動画を見る
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
【中学からの!】三角比の計算(3):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
この動画を見る
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
【中学からの!】三角比の計算(2):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
【中学からの!】三角比の計算(1):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
福田の数学〜慶應義塾大学2022年総合政策学部第4問〜折り紙を折ってできる線分、角、面積を求める
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが2の正方形の折り紙 ABCD を次の手順にしたがって折る。
(1) A と B、DとCを合わせて ADがBCに重なるように谷折りし、折り目をつけて
開く。AB および DC 上にあるこの谷折り線の端点をそれぞれEおよびFとする。
(2 ) AF が谷折り線になるよう に谷折りし、折り目をつけて開く。
(3) A を谷折り線の端点の1つとして、AB がAF 上に重なるように谷折りし、折り
目をつけて開く。BC上にあるこの谷折り線のもう1つの端点をGとする。
(4) D と A、CとBを合わせてDCがABに重なるように谷折りして、折り目をつけ
る。AD およびBC 上にあるこの谷折り線の端点をそれぞれHおよびIとする。
(5) C と B がいずれもGと重なるように2枚重ねて谷折りし、CIおよびBI 上に折り
目をつけて開く。この折り目の点をそれぞれ」およびKとする (A, E, B, K は
それぞれ D, F, C, J と重なっているため図中には表示していない)
(6) HI を谷折り線とする谷折りを開く (A, E, B, KはそれぞれD, F, C, J と重なって
いるため図中には表示していない)
(7) K を谷折り線の端点の1つとして、JがAB上に重なるように谷折りし、折り目
をつける。AD上にあるこの谷折り線のもう1つの端点をしとし、AB上にある
Jが重なる点をMとする。
(8)KLを谷折り戦とする谷折りを開く(MはJと重なっているため表示していない)
(9)Mを谷折り線の端点の1つとして、AとDがそれぞれBEとCF上にくるように
谷折りし、折り目をつけて開く。DC上にあるこの谷折り線のもう1つ端点を
Nとする。
(10)折るのをやめる。
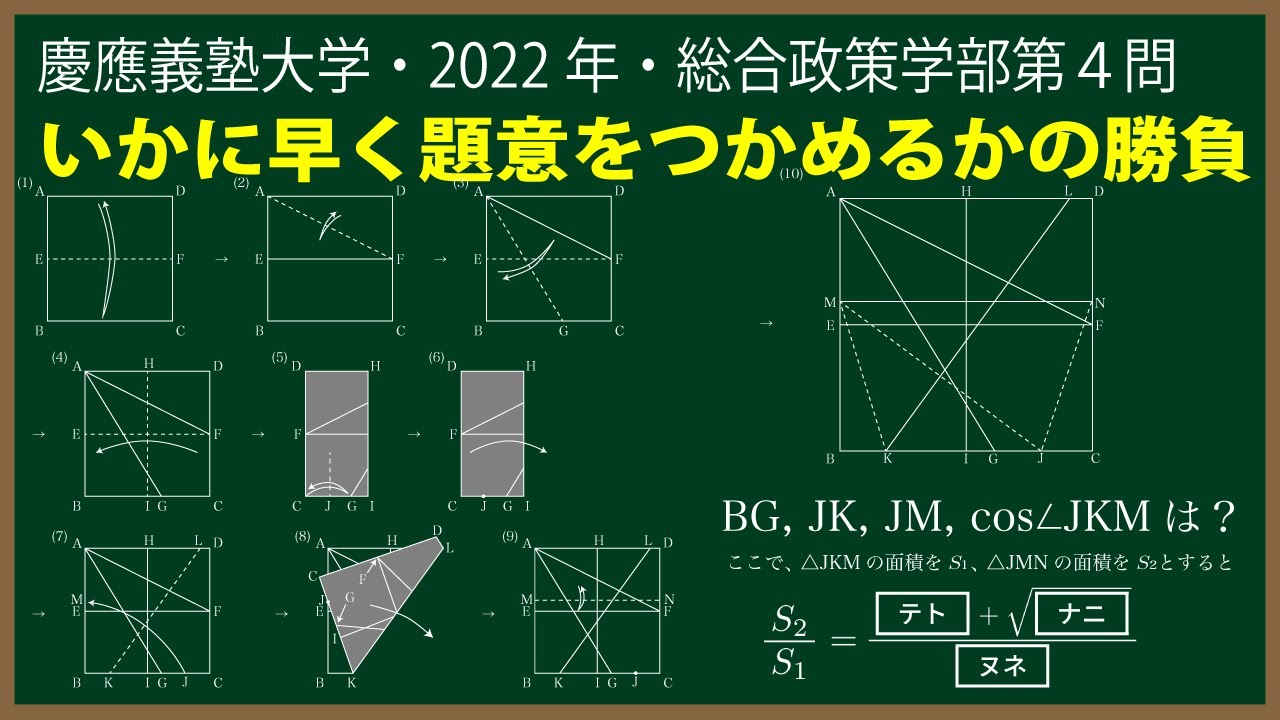
このとき、
$BG=\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }},JK=\boxed{\ \ オカ\ \ }+\sqrt{\boxed{\ \ キク\ \ }},JM=\boxed{\ \ ケコ\ \ },$
$\cos\angle JKM=\frac{\boxed{\ \ サシ\ \ }+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }}$
ここで、$\triangle JKM$の面積を$S_1,\triangle JMN$の面積を$S_2$とすると
$\frac{S_2}{S_1}=\frac{\boxed{\ \ テト\ \ }+\sqrt{\boxed{\ \ ナニ\ \ }}}{\boxed{\ \ ヌネ\ \ }}$
となる。
※(1)~(10)の画像は動画参照
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが2の正方形の折り紙 ABCD を次の手順にしたがって折る。
(1) A と B、DとCを合わせて ADがBCに重なるように谷折りし、折り目をつけて
開く。AB および DC 上にあるこの谷折り線の端点をそれぞれEおよびFとする。
(2 ) AF が谷折り線になるよう に谷折りし、折り目をつけて開く。
(3) A を谷折り線の端点の1つとして、AB がAF 上に重なるように谷折りし、折り
目をつけて開く。BC上にあるこの谷折り線のもう1つの端点をGとする。
(4) D と A、CとBを合わせてDCがABに重なるように谷折りして、折り目をつけ
る。AD およびBC 上にあるこの谷折り線の端点をそれぞれHおよびIとする。
(5) C と B がいずれもGと重なるように2枚重ねて谷折りし、CIおよびBI 上に折り
目をつけて開く。この折り目の点をそれぞれ」およびKとする (A, E, B, K は
それぞれ D, F, C, J と重なっているため図中には表示していない)
(6) HI を谷折り線とする谷折りを開く (A, E, B, KはそれぞれD, F, C, J と重なって
いるため図中には表示していない)
(7) K を谷折り線の端点の1つとして、JがAB上に重なるように谷折りし、折り目
をつける。AD上にあるこの谷折り線のもう1つの端点をしとし、AB上にある
Jが重なる点をMとする。
(8)KLを谷折り戦とする谷折りを開く(MはJと重なっているため表示していない)
(9)Mを谷折り線の端点の1つとして、AとDがそれぞれBEとCF上にくるように
谷折りし、折り目をつけて開く。DC上にあるこの谷折り線のもう1つ端点を
Nとする。
(10)折るのをやめる。
このとき、
$BG=\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }},JK=\boxed{\ \ オカ\ \ }+\sqrt{\boxed{\ \ キク\ \ }},JM=\boxed{\ \ ケコ\ \ },$
$\cos\angle JKM=\frac{\boxed{\ \ サシ\ \ }+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }}$
ここで、$\triangle JKM$の面積を$S_1,\triangle JMN$の面積を$S_2$とすると
$\frac{S_2}{S_1}=\frac{\boxed{\ \ テト\ \ }+\sqrt{\boxed{\ \ ナニ\ \ }}}{\boxed{\ \ ヌネ\ \ }}$
となる。
※(1)~(10)の画像は動画参照
2022慶應義塾大学総合政策学部過去問
【中学生から理解できる!】三角比(さんかくひ)[ エッセンシャル版 ]:~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三角比に関して解説していきます.
この動画を見る
三角比に関して解説していきます.
阪大の証明問題!解けますか?【数学 入試問題】【大阪大学 理系】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の自然数とする。三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。$ \angle ACB=n \angle ABC$であるとき,$ c<nb $を示せ。
大阪大理系過去問
この動画を見る
$n$を2以上の自然数とする。三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。$ \angle ACB=n \angle ABC$であるとき,$ c<nb $を示せ。
大阪大理系過去問
阪大の証明問題!ぜひとも取りたい問題【数学 入試問題】【大阪大学 文系】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。
$\angle ACB=3\angle ABC$であるとき,$c<3b$を示せ。
大阪大過去問
この動画を見る
三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。
$\angle ACB=3\angle ABC$であるとき,$c<3b$を示せ。
大阪大過去問
福田の数学〜慶應義塾大学2022年経済学部第1問〜円に外接する四角形の性質

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の四角形ABCDは以下の条件を満たすとする。
$(\textrm{a})$頂点Aの座標は(-1,-1)である。
$(\textrm{b})$四角形の各辺は原点を中心とする半径1の円と接する。
$(\textrm{c})$$\angle BCD$は直角である。
また、辺ABの長さをlとし、$\angle ABC=\theta$とする。
(1)$\angle BAD=\frac{\pi}{\boxed{\ \ ア\ \ }}$である。
(2)辺CDの長さが$\frac{5}{3}$であるとき、$l=\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},\ \tan\theta=\frac{\boxed{\ \ エオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\theta$は鋭角とする。四角形ABCDの面積が6であるとき、$l=\boxed{\ \ キ\ \ }+\sqrt{\boxed{\ \ ク\ \ }}$ ,
$\theta = \frac{\pi}{\boxed{\ \ ケ\ \ }}$である。
2022慶應義塾大学経済学部過去問
この動画を見る
座標平面上の四角形ABCDは以下の条件を満たすとする。
$(\textrm{a})$頂点Aの座標は(-1,-1)である。
$(\textrm{b})$四角形の各辺は原点を中心とする半径1の円と接する。
$(\textrm{c})$$\angle BCD$は直角である。
また、辺ABの長さをlとし、$\angle ABC=\theta$とする。
(1)$\angle BAD=\frac{\pi}{\boxed{\ \ ア\ \ }}$である。
(2)辺CDの長さが$\frac{5}{3}$であるとき、$l=\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},\ \tan\theta=\frac{\boxed{\ \ エオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\theta$は鋭角とする。四角形ABCDの面積が6であるとき、$l=\boxed{\ \ キ\ \ }+\sqrt{\boxed{\ \ ク\ \ }}$ ,
$\theta = \frac{\pi}{\boxed{\ \ ケ\ \ }}$である。
2022慶應義塾大学経済学部過去問
