数Ⅰ
数Ⅰ
この因数分解できますか？
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
因数分解しなさい。
$ab(a+b)+bc(b+c)+ca(c+a)+2abc$
この動画を見る
因数分解しなさい。
$ab(a+b)+bc(b+c)+ca(c+a)+2abc$
福田のおもしろ数学494〜3乗根の付いた数の大小比較
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
この動画を見る
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
福田のおもしろ数学490〜3乗根混じりの2重根号を解消
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
この動画を見る
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
これ知ってた？
単元：
#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$(x+a)^{ 2 }=x^{ 2 }+2ax+a^{ 2 }$の考え方
この動画を見る
$(x+a)^{ 2 }=x^{ 2 }+2ax+a^{ 2 }$の考え方
福田の数学〜慶應義塾大学看護医療学部2025第5問〜データの分析、平均と分散
単元：
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
(1)$20$人の生徒に、$5$点満点の小テストを行った。
次の度数分布表は全員のテストの得点である。
この小テストの得点の平均値は$\boxed{ハ}$、
分散は$\boxed{ヒ}$である。
また、生徒のうちの$1$名の得点が$\boxed{フ}$点から
$\boxed{ヘ}$点に変更された場合、
生徒全員の得点の平均値は$3$、分散は$2$となる。
(2)確率変数$X$と$Y$は独立であり、$X$の平均が$m_x$、
分散が$\upsilon_x$であるとする。
また、$a,b$は定数とする。このとき、$aX+bY$の
平均は$\boxed{ホ}$、分散は$\boxed{マ}$である。
(3)確率変数$X_1,X_2,\cdots,X_n,X_{n+1}$は互いに
独立であり、
$T_n=\dfrac{1}{n}(X_1+X_2+\cdots + X_n)$
の平均が$m$、分散が$\upsilon$であるとする。
$X_{n+1}$の平均が$m'$、分散が$\upsilon'$であるとき、
$T_{n+1}=\dfrac{1}{n+1}(X_1+X_2+\cdots +X_n+X_{n+1})$
の平均は$\boxed{ミ}$、分散は$\boxed{ム}$である。
図は動画内参照
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{5}$
(1)$20$人の生徒に、$5$点満点の小テストを行った。
次の度数分布表は全員のテストの得点である。
この小テストの得点の平均値は$\boxed{ハ}$、
分散は$\boxed{ヒ}$である。
また、生徒のうちの$1$名の得点が$\boxed{フ}$点から
$\boxed{ヘ}$点に変更された場合、
生徒全員の得点の平均値は$3$、分散は$2$となる。
(2)確率変数$X$と$Y$は独立であり、$X$の平均が$m_x$、
分散が$\upsilon_x$であるとする。
また、$a,b$は定数とする。このとき、$aX+bY$の
平均は$\boxed{ホ}$、分散は$\boxed{マ}$である。
(3)確率変数$X_1,X_2,\cdots,X_n,X_{n+1}$は互いに
独立であり、
$T_n=\dfrac{1}{n}(X_1+X_2+\cdots + X_n)$
の平均が$m$、分散が$\upsilon$であるとする。
$X_{n+1}$の平均が$m'$、分散が$\upsilon'$であるとき、
$T_{n+1}=\dfrac{1}{n+1}(X_1+X_2+\cdots +X_n+X_{n+1})$
の平均は$\boxed{ミ}$、分散は$\boxed{ム}$である。
図は動画内参照
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学486〜1分チャレンジ！無理数の計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
この動画を見る
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
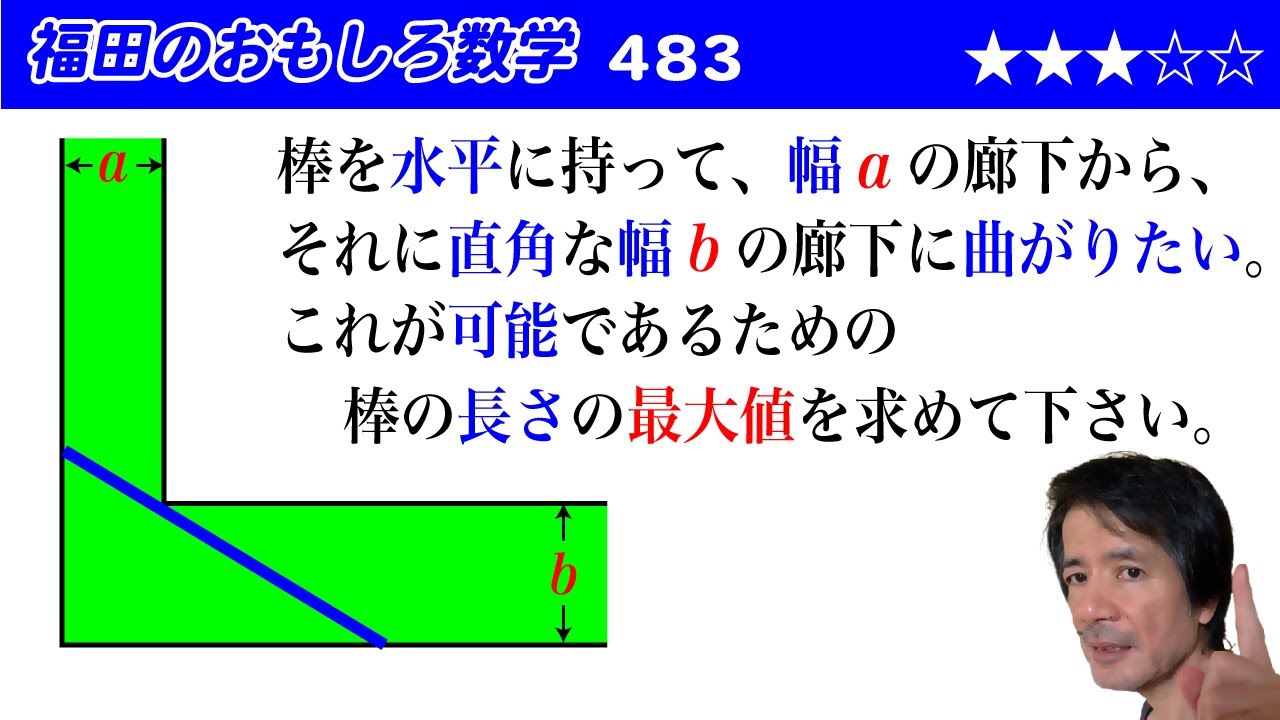
福田のおもしろ数学483〜直角に曲がった廊下を曲がれる棒の長さの最大値
単元：
#数Ⅰ#数A#図形の性質#図形と計量#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
棒を水平に持って、幅$a$の廊下から、
それに直角な幅$b$の廊下に曲がりたい。
これが可能であるための
棒の長さの最大値を求めて下さい。
図は動画内参照
この動画を見る
棒を水平に持って、幅$a$の廊下から、
それに直角な幅$b$の廊下に曲がりたい。
これが可能であるための
棒の長さの最大値を求めて下さい。
図は動画内参照
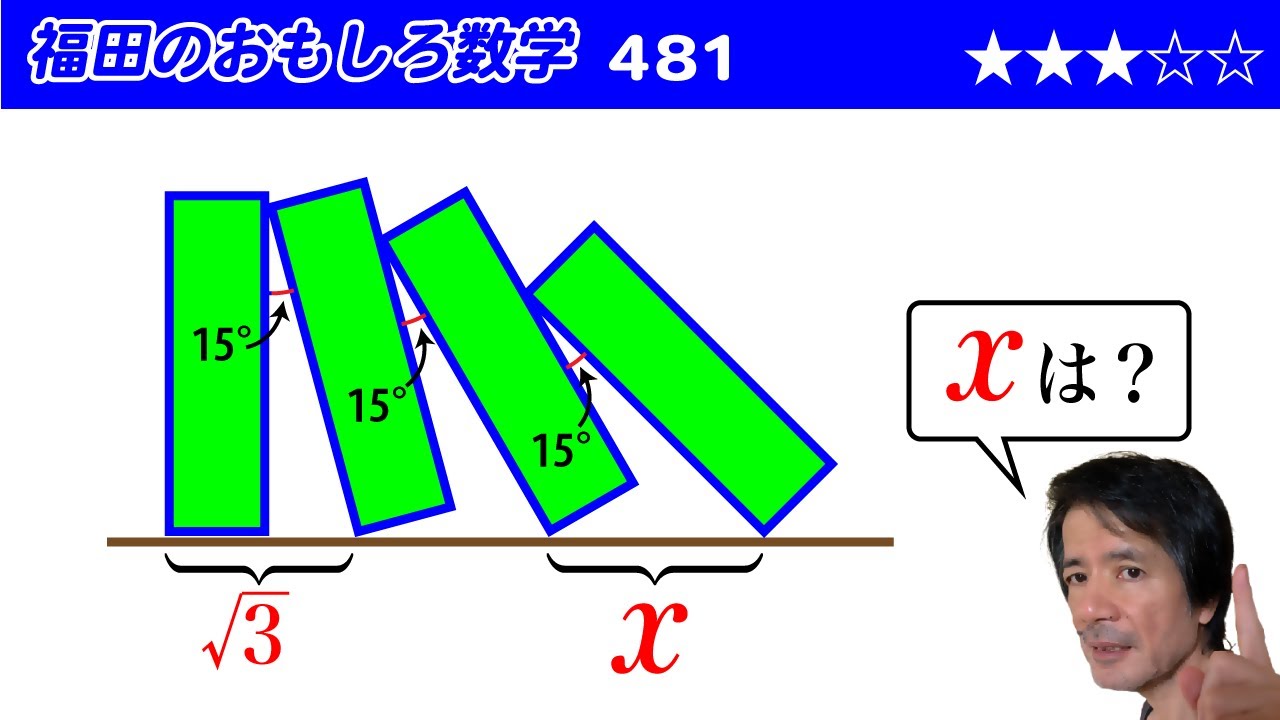
福田のおもしろ数学481〜長方形が15°ずつ傾いてずれていく
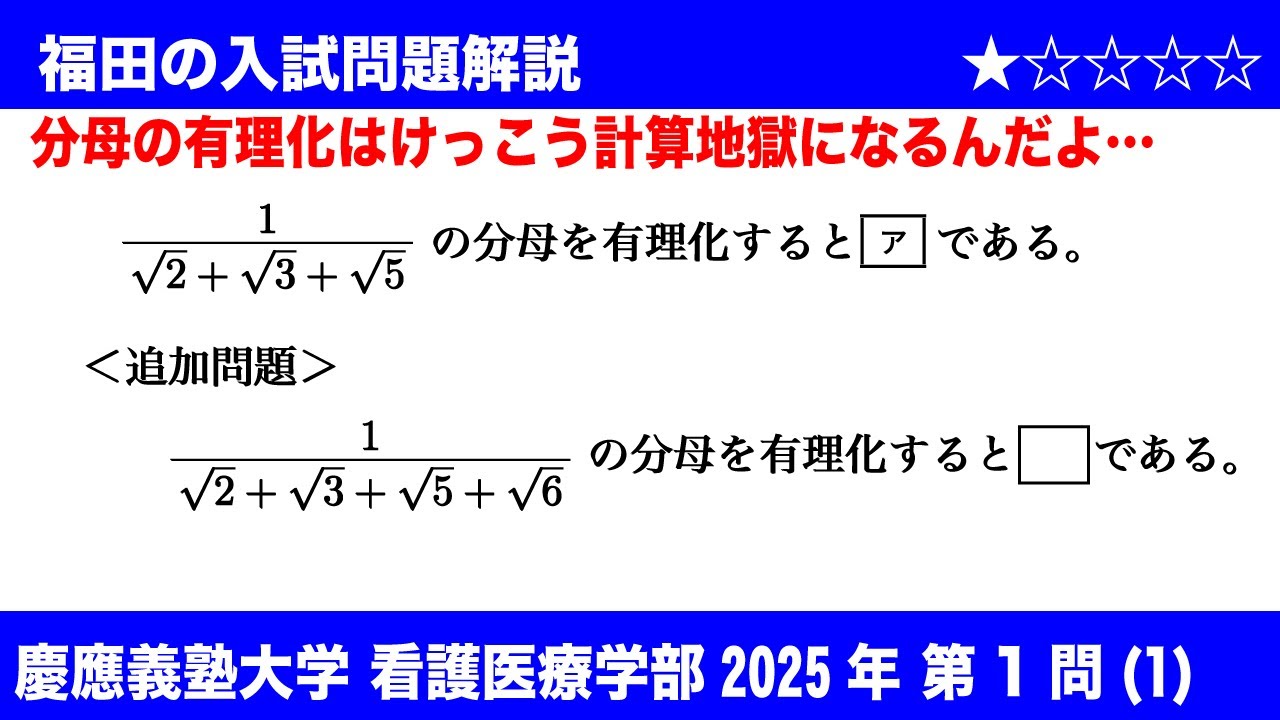
福田の数学〜慶應義塾大学看護医療学部2025第1問(1)〜分母の有理化
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
福田の数学〜早稲田大学理工学部2025第2問〜領域に含まれる三角形の面積の最大値
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
福田のおもしろ数学474〜3変数の関係からa+b+cの値を求める
単元：
#連立方程式#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
この動画を見る
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
福田の数学〜慶應義塾大学薬学部2025第1問(1)〜絶対不等式と2次関数の最大最小
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜北海道大学2025文系第2問〜数え上げと余弦定理
単元：
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用（正弦・余弦・面積）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
整数$a,b,c$は条件
$2\leqq a \lt b \lt c \leqq 6$を満たすとする。
(1)不等式$a+b\gt c$を満たすような
$(a+b+c)$をすべて挙げよ。
(2)不等式$a^2+b^2\geqq c^2$を満たすような
$(a+b+c)$をすべて挙げよ。
(3) (2)で求めた$(a,b,c)$について、
頂点$A,B,C$と向かい合う辺の長さがそれぞれ
$a,b,c$で与えられる$\triangle ABC$を考える。
このようなすべての$\triangle ABC$について
$\cos \angle ACB$を求めよ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{2}$
整数$a,b,c$は条件
$2\leqq a \lt b \lt c \leqq 6$を満たすとする。
(1)不等式$a+b\gt c$を満たすような
$(a+b+c)$をすべて挙げよ。
(2)不等式$a^2+b^2\geqq c^2$を満たすような
$(a+b+c)$をすべて挙げよ。
(3) (2)で求めた$(a,b,c)$について、
頂点$A,B,C$と向かい合う辺の長さがそれぞれ
$a,b,c$で与えられる$\triangle ABC$を考える。
このようなすべての$\triangle ABC$について
$\cos \angle ACB$を求めよ。
$2025$年北海道大学文系過去問題
福田の数学〜京都大学2025理系第4問〜平面が定点を通過する条件
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
福田のおもしろ数学430〜整式を満たす整数解の性質
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
整数係数の整式$P(x)$に対して
$P(x)=1$と$P(x)＝3＄がともに整数解をもつとき、
$P(x)=2$
は異なる$2$つの整数解をもてるか？
この動画を見る
整数係数の整式$P(x)$に対して
$P(x)=1$と$P(x)＝3＄がともに整数解をもつとき、
$P(x)=2$
は異なる$2$つの整数解をもてるか？
福田のおもしろ数学428〜√n+1-√n-1が有理数になるような整数nが存在するかどうかを考える
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{n+1}-\sqrt{n-1}$が有理数となる
整数$n$は存在するか？
この動画を見る
$\sqrt{n+1}-\sqrt{n-1}$が有理数となる
整数$n$は存在するか？
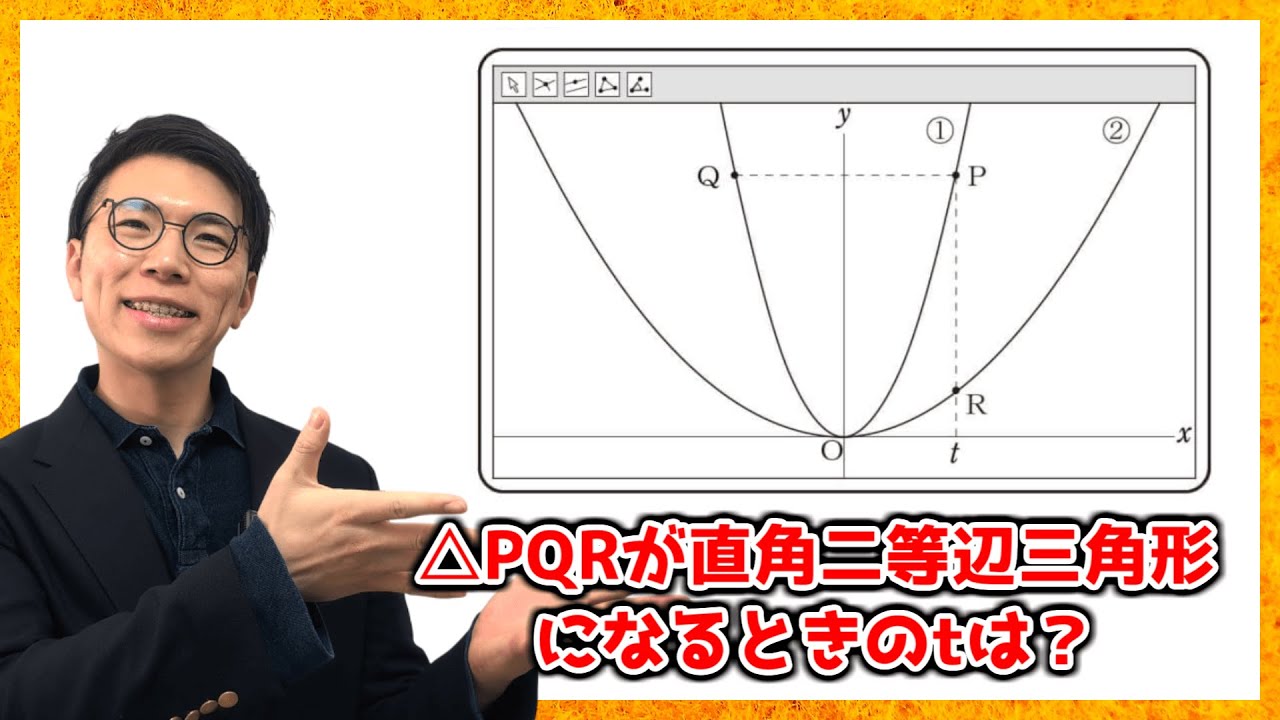
【中学数学】2次関数の問題～2024年度北海道公立高校入試大問3～【高校受験】
単元：
#数学(中学生)#中３数学#数Ⅰ#２次関数#2次関数#2次関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①，$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$＞0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ？△PQRが直角に等辺三角形に見えるときがあるよ？」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
この動画を見る
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①，$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$＞0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ？△PQRが直角に等辺三角形に見えるときがあるよ？」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
福田の数学〜東京大学2025理系第4問〜関数の値が平方数となる条件
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
【中学生の方が解ける…!?】図形：駿台甲府高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#数Ⅰ#図形と計量
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
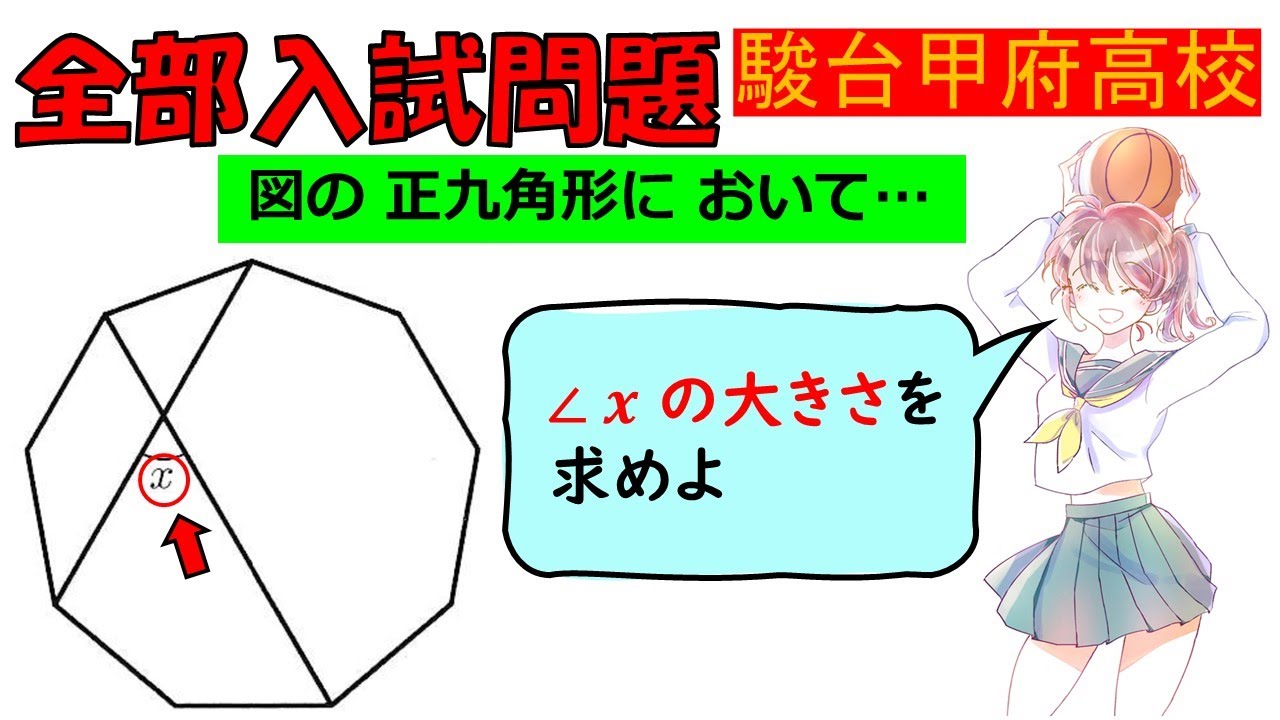
図の正九角形において
$\angle x$の大きさを求めよ
この動画を見る
図の正九角形において
$\angle x$の大きさを求めよ
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
【初めの一手は…！】二次方程式：中央大学杉並高等学校～全国入試問題解法
単元：
#数学(中学生)#数Ⅰ#高校入試過去問(数学)#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
この動画を見る
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
福田のおもしろ数学410〜条件を満たすKの最大値
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
この動画を見る
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
【スッキリ理解できる…！】一次関数：駿台甲府高等学校～全国入試問題解法
単元：
#図形と計量#平面図形#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
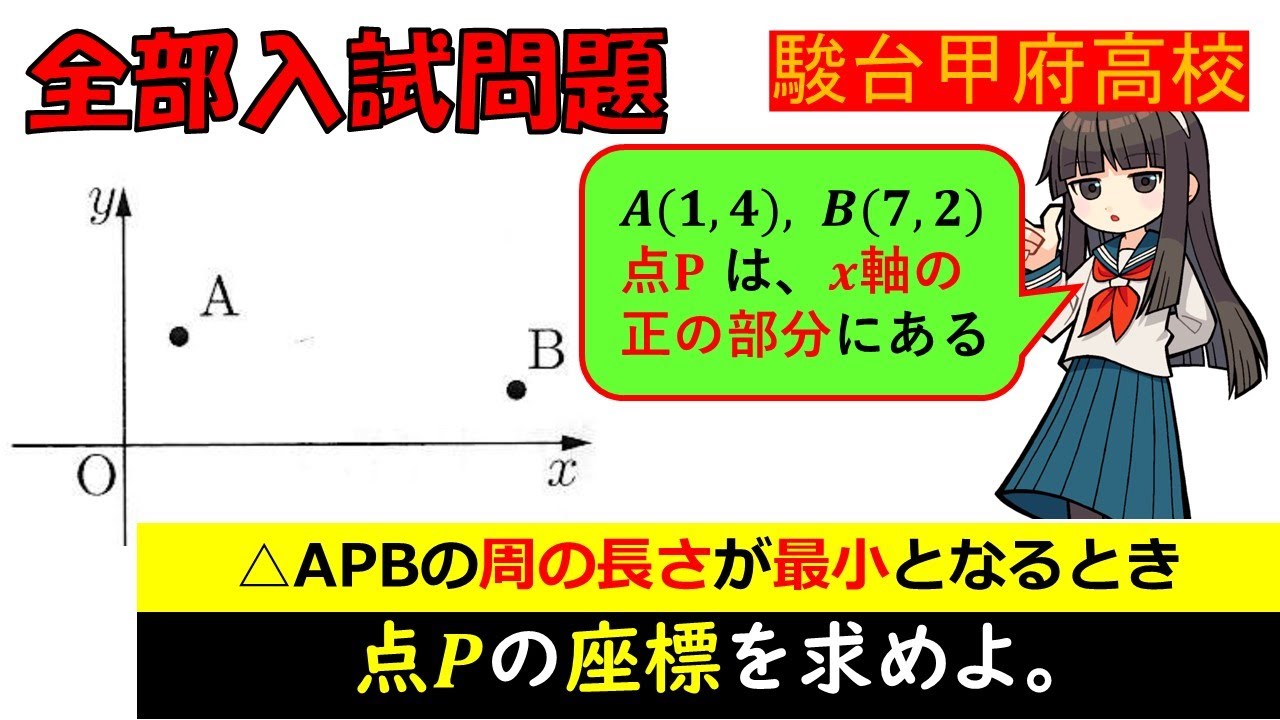
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
この動画を見る
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
【入試で必要な発想…！】図形：明治学院高等学校～全国入試問題解法
単元：
#数学(中学生)#数Ⅰ#図形と計量#平面図形#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
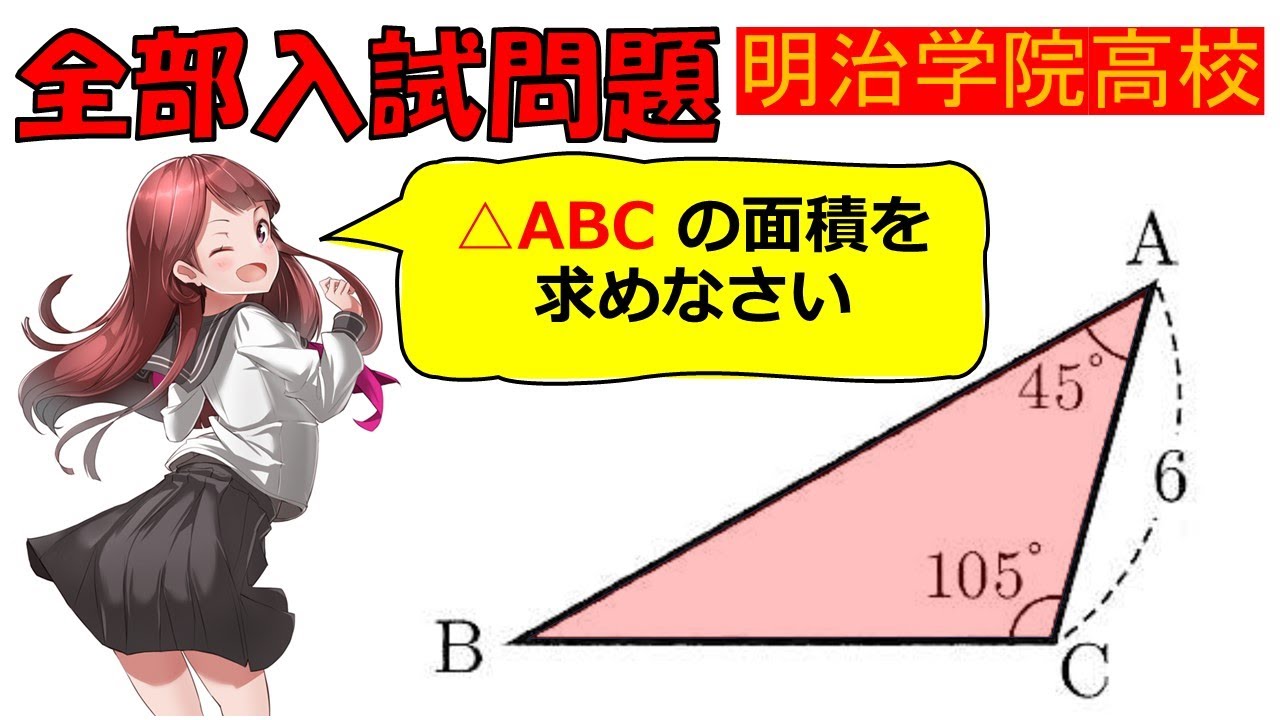
$\triangleABCの面積を求めなさい$
この動画を見る
$\triangleABCの面積を求めなさい$
【数Ⅰ】【図形と計量】測量の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
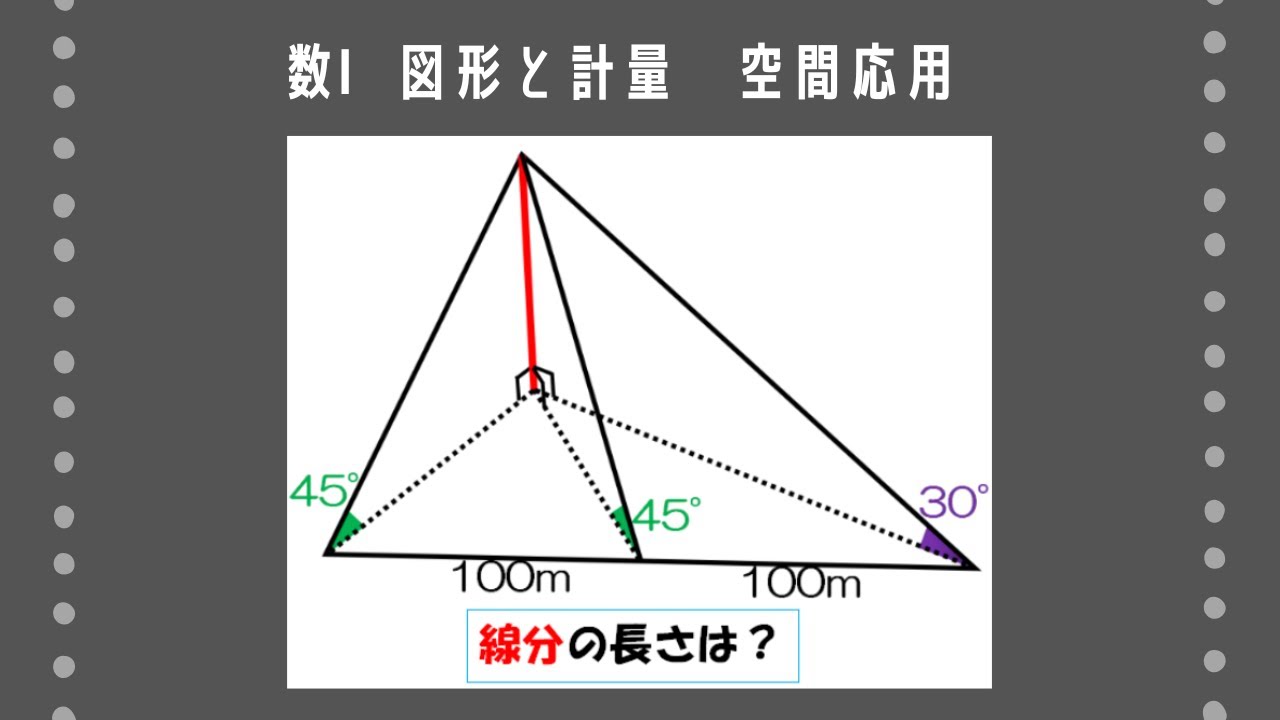
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
この動画を見る
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
【数Ⅰ】【図形と計量】測量の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
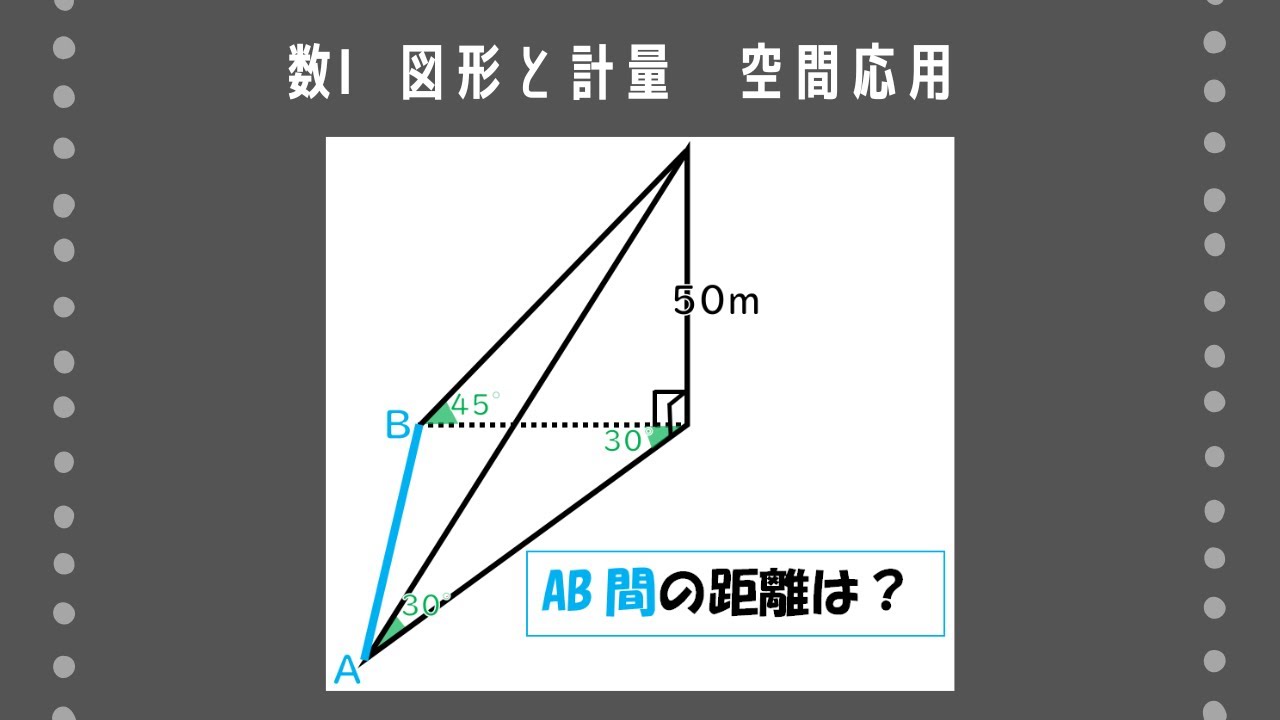
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
この動画を見る
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
【数Ⅰ】【図形と計量】球2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
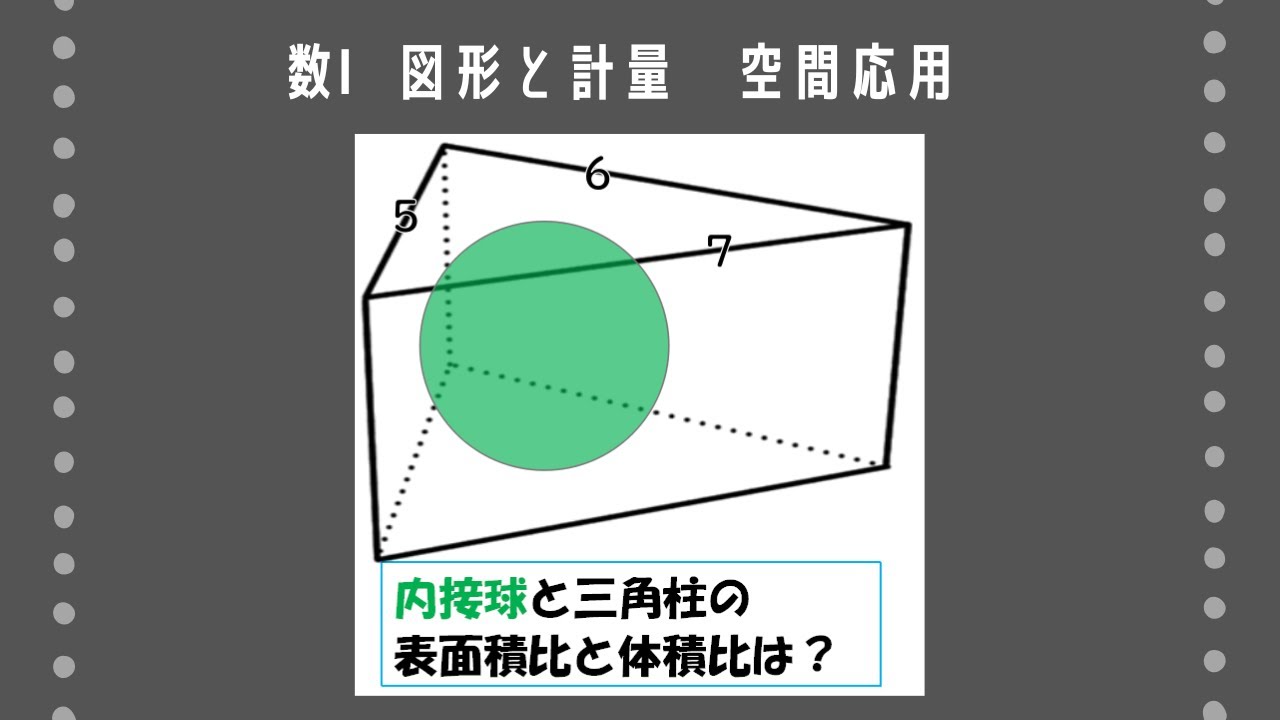
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
この動画を見る
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
【数Ⅰ】【図形と計量】球1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
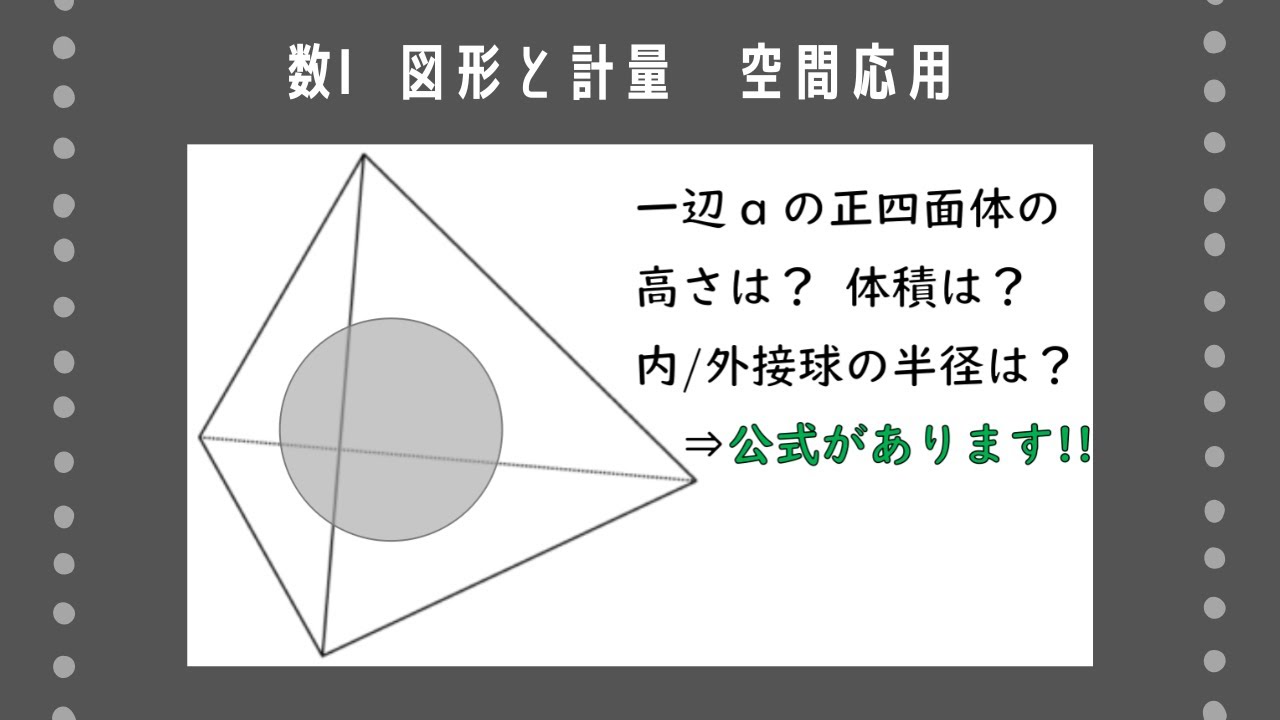
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
この動画を見る
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
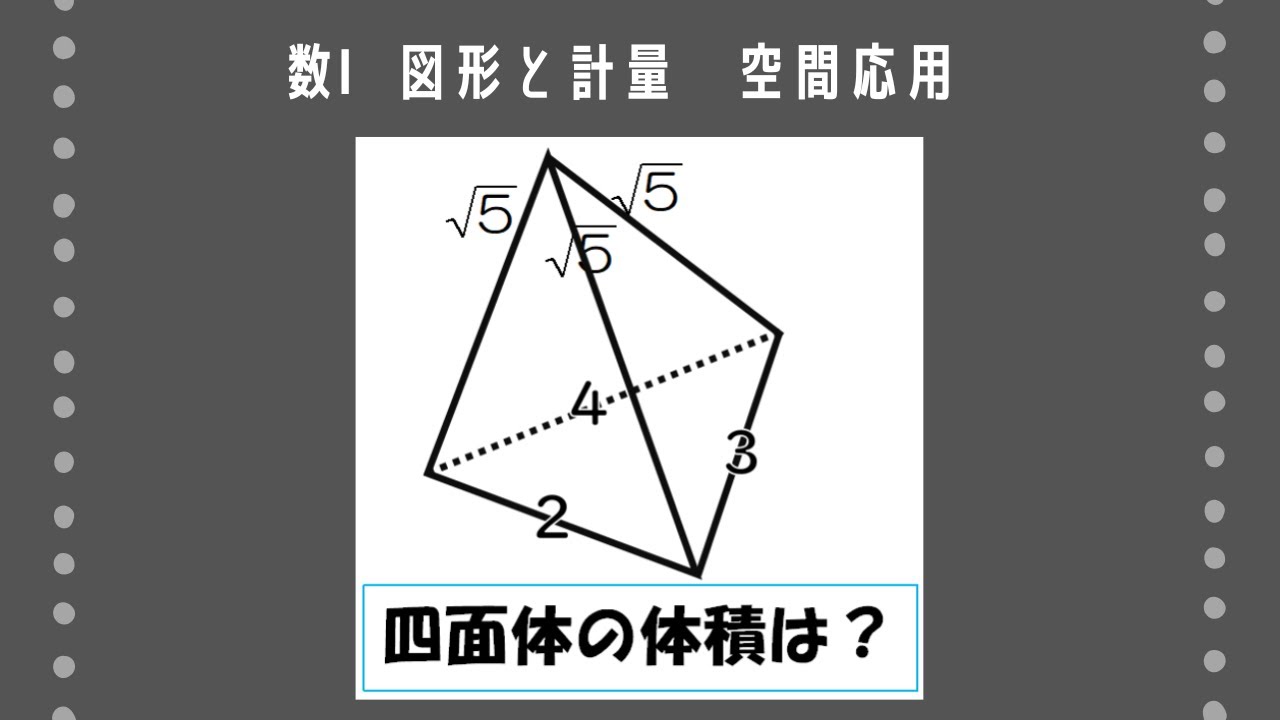
$\rm PA＝PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
この動画を見る
$\rm PA＝PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
この動画を見る
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。