数Ⅰ
数Ⅰ
【初めの一手は…！】二次方程式：中央大学杉並高等学校～全国入試問題解法
単元：
#数学(中学生)#数Ⅰ#高校入試過去問(数学)#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
この動画を見る
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
福田のおもしろ数学410〜条件を満たすKの最大値
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
この動画を見る
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
【スッキリ理解できる…！】一次関数：駿台甲府高等学校～全国入試問題解法
単元：
#図形と計量#平面図形#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
この動画を見る
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
【入試で必要な発想…！】図形：明治学院高等学校～全国入試問題解法
単元：
#数学(中学生)#数Ⅰ#図形と計量#平面図形#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\triangleABCの面積を求めなさい$
この動画を見る
$\triangleABCの面積を求めなさい$
【数Ⅰ】【図形と計量】測量の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
この動画を見る
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
【数Ⅰ】【図形と計量】測量の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
この動画を見る
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
【数Ⅰ】【図形と計量】球2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
この動画を見る
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
【数Ⅰ】【図形と計量】球1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
この動画を見る
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\rm PA＝PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
この動画を見る
$\rm PA＝PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
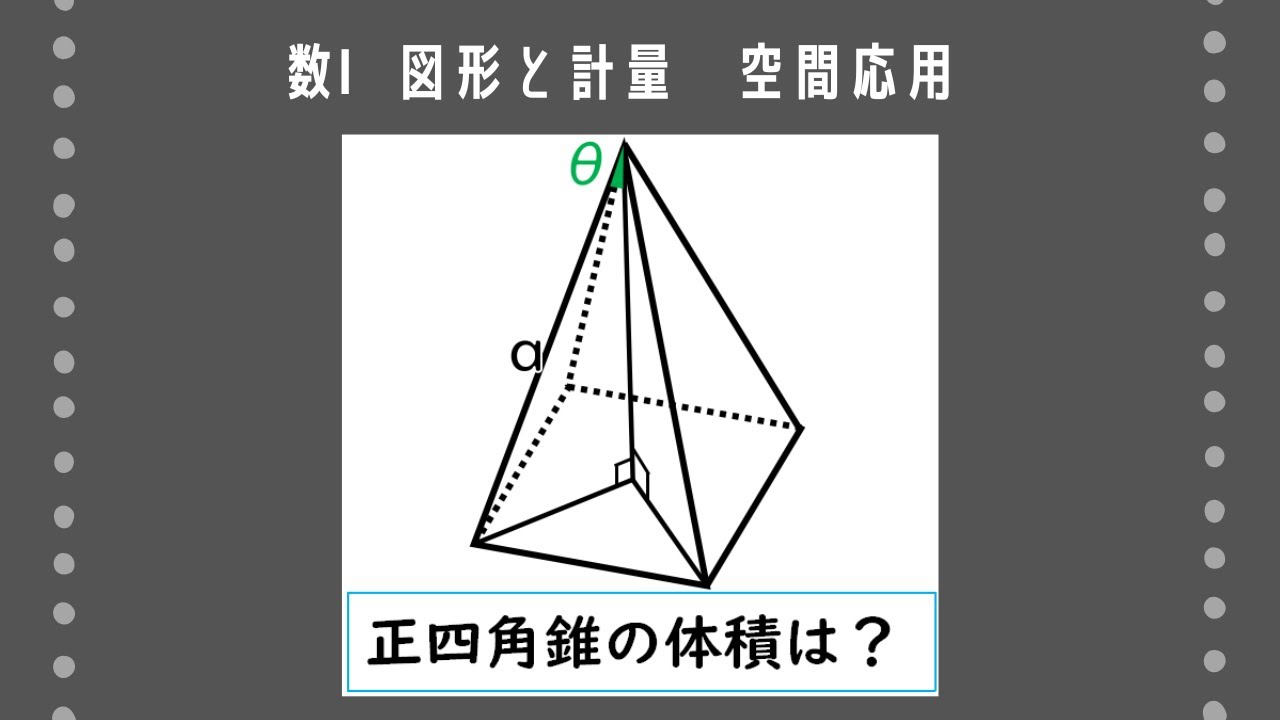
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
この動画を見る
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
【数Ⅰ】【図形と計量】空間の基本2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
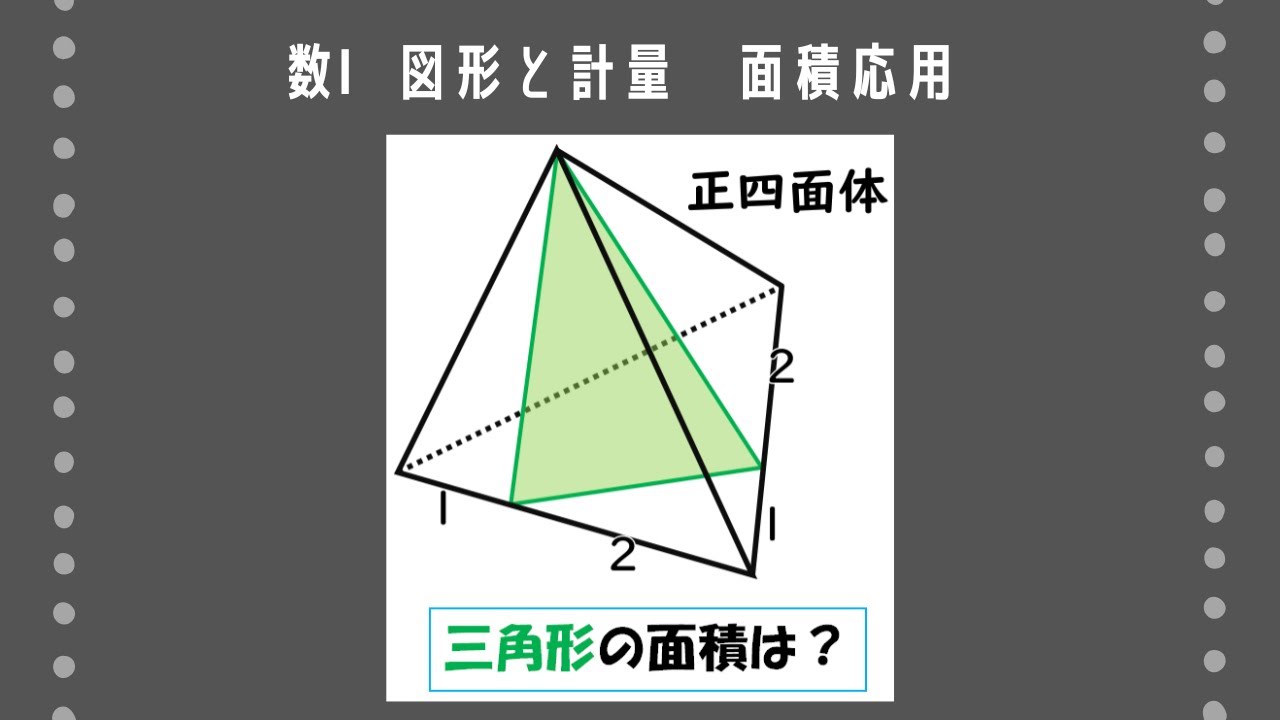
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
この動画を見る
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
【数Ⅰ】【図形と計量】空間の基本3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
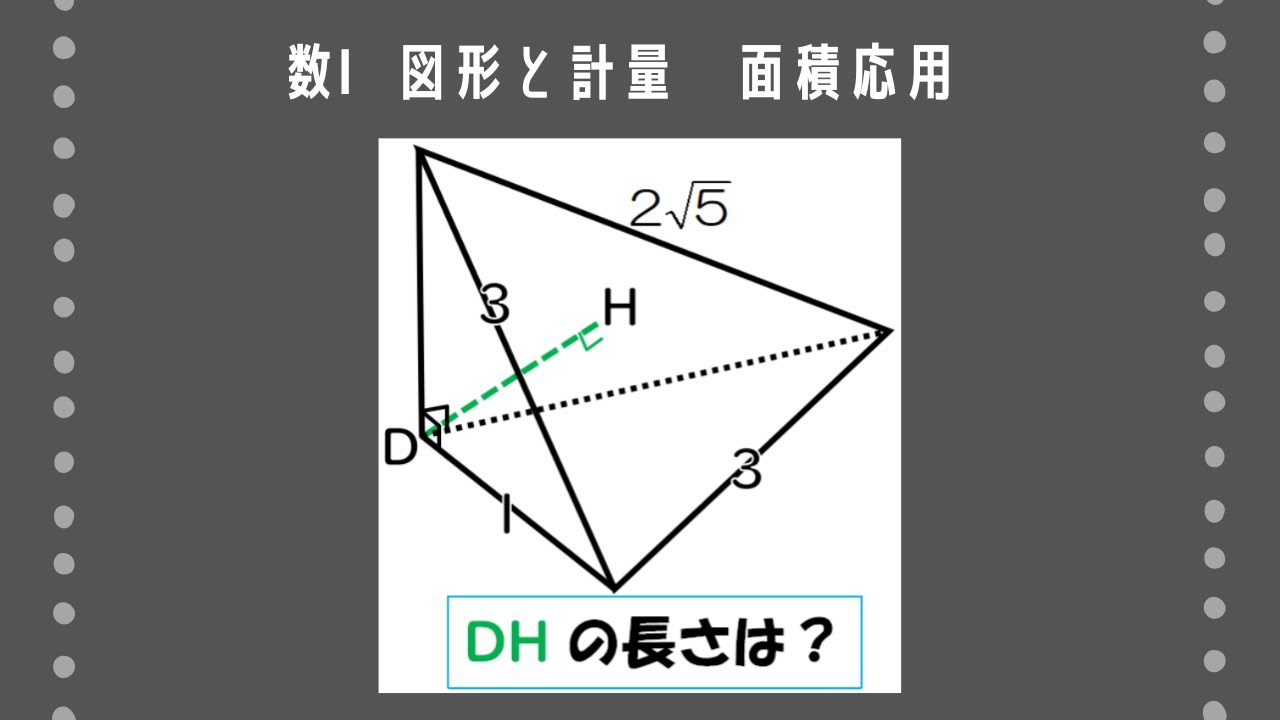
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
この動画を見る
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
【数Ⅰ】【図形と計量】空間の基本1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
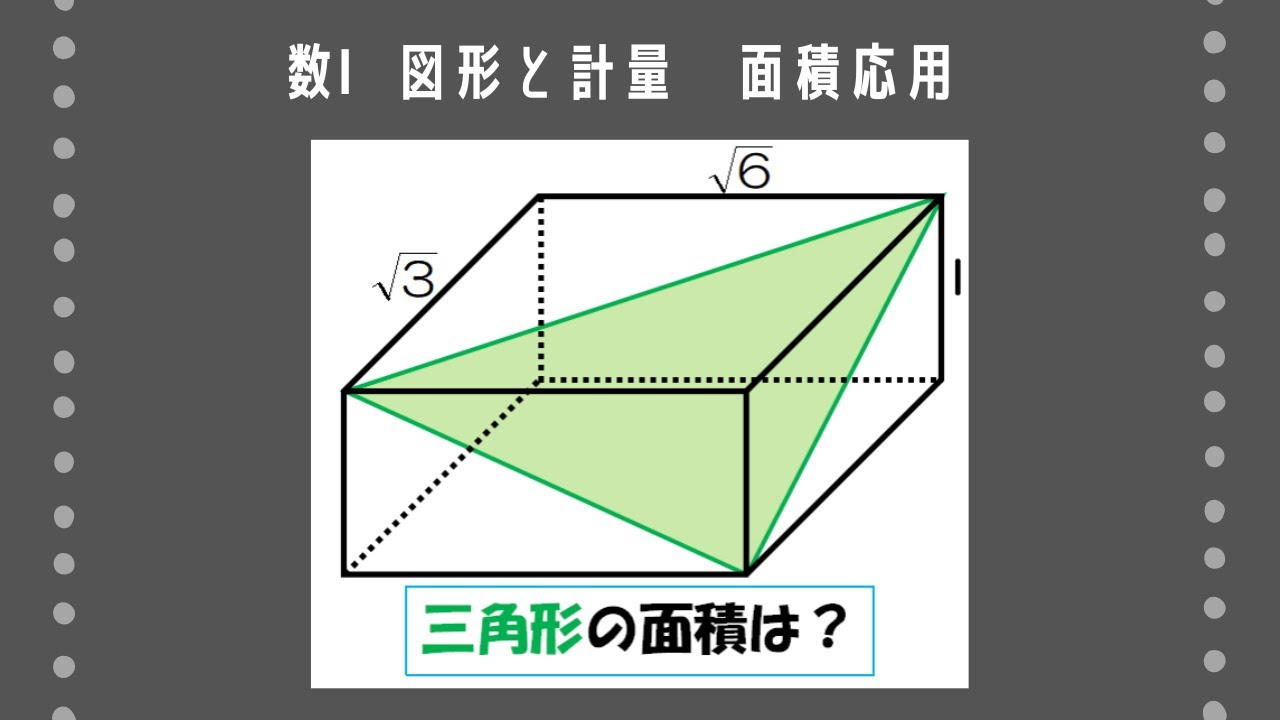
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
この動画を見る
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
【数Ⅰ】【図形と計量】面積応用10 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
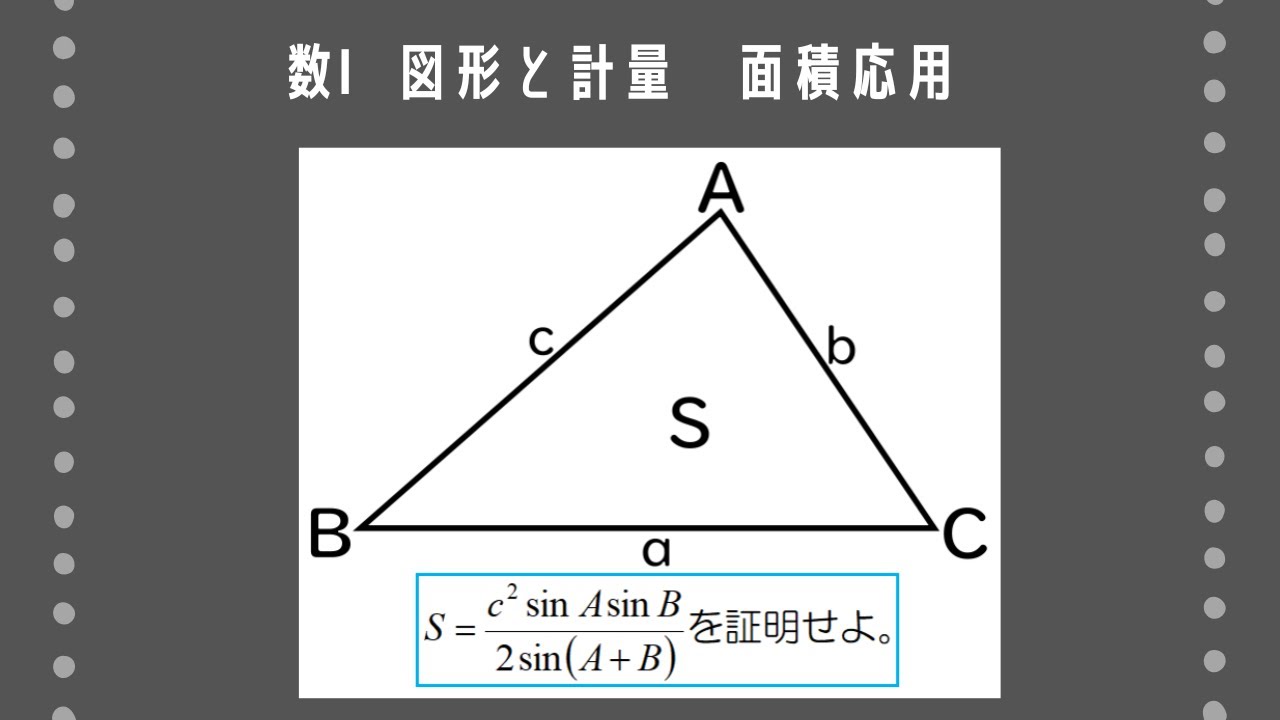
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
この動画を見る
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
【数Ⅰ】【図形と計量】面積応用9 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
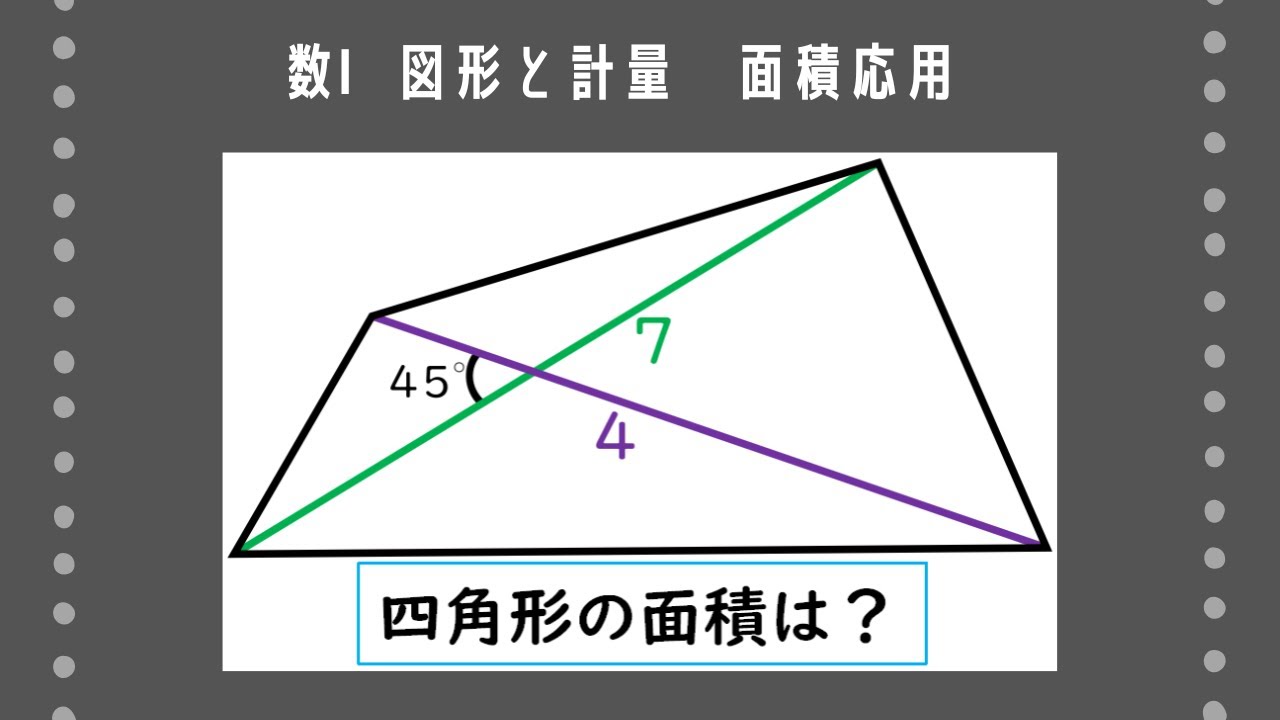
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
この動画を見る
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
【数Ⅰ】【図形と計量】面積応用8 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
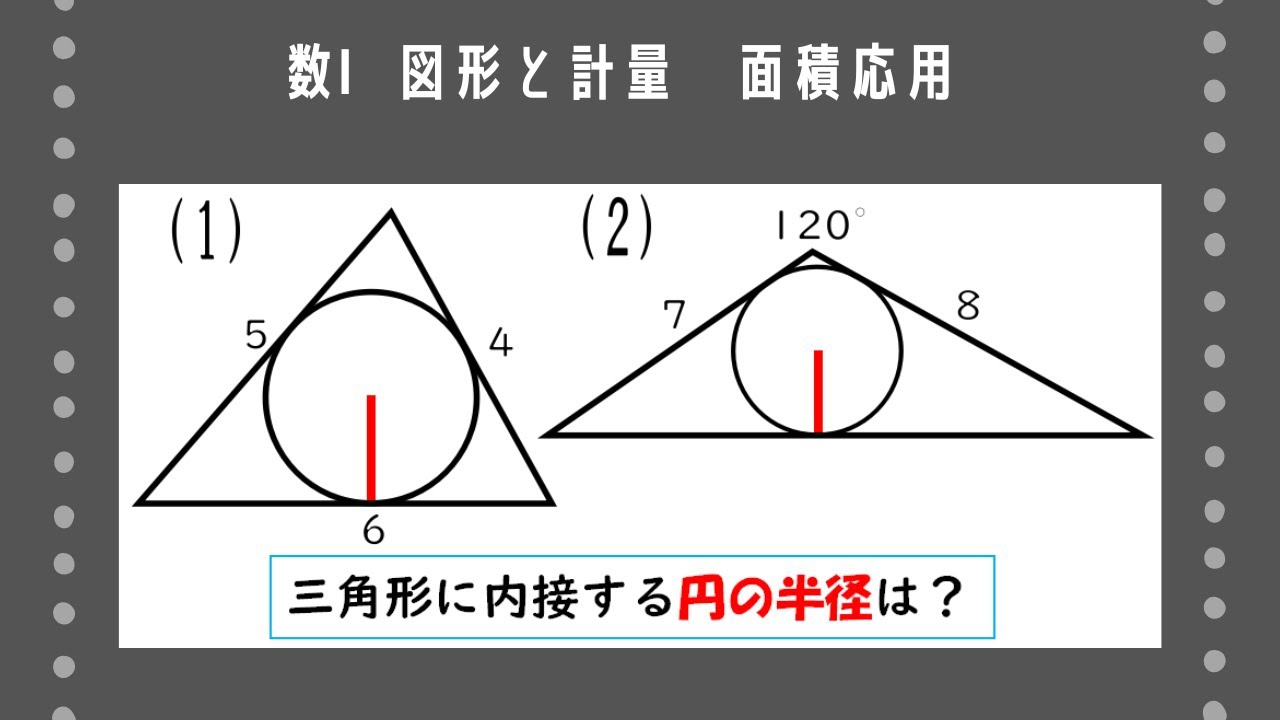
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
この動画を見る
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
２つの二次方程式 2025立教新座
単元：
#２次関数#2次方程式と2次不等式
指導講師：
数学を数楽に
問題文全文(内容文)：
2つの2次方程式 \begin{eqnarray}
x^2 -kx-10 = 0
\end{eqnarray}
\begin{eqnarray}
x^2+5x+2k=0
\end{eqnarray}
が共通解を1つだけ持つ。この共通解と定数kを求めよ。ただしk≠-5
この動画を見る
2つの2次方程式 \begin{eqnarray}
x^2 -kx-10 = 0
\end{eqnarray}
\begin{eqnarray}
x^2+5x+2k=0
\end{eqnarray}
が共通解を1つだけ持つ。この共通解と定数kを求めよ。ただしk≠-5
【数Ⅰ】【図形と計量】面積応用3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
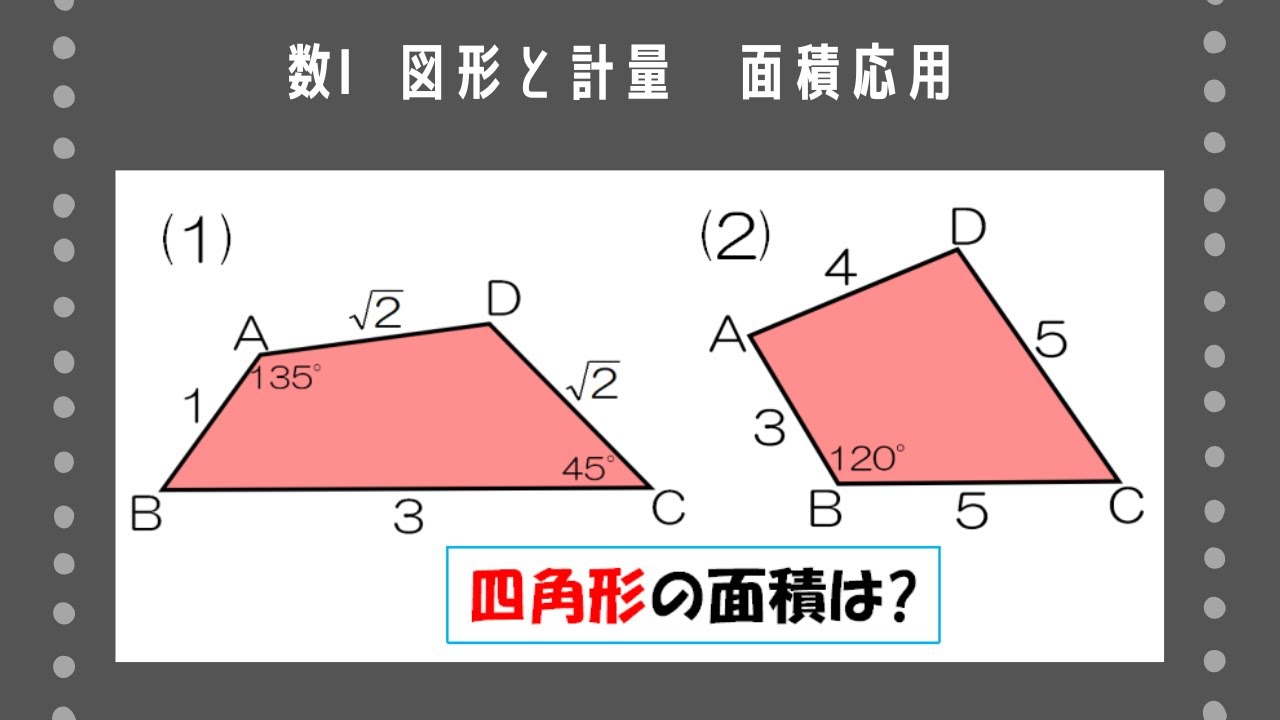
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
【数Ⅰ】【図形と計量】面積応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
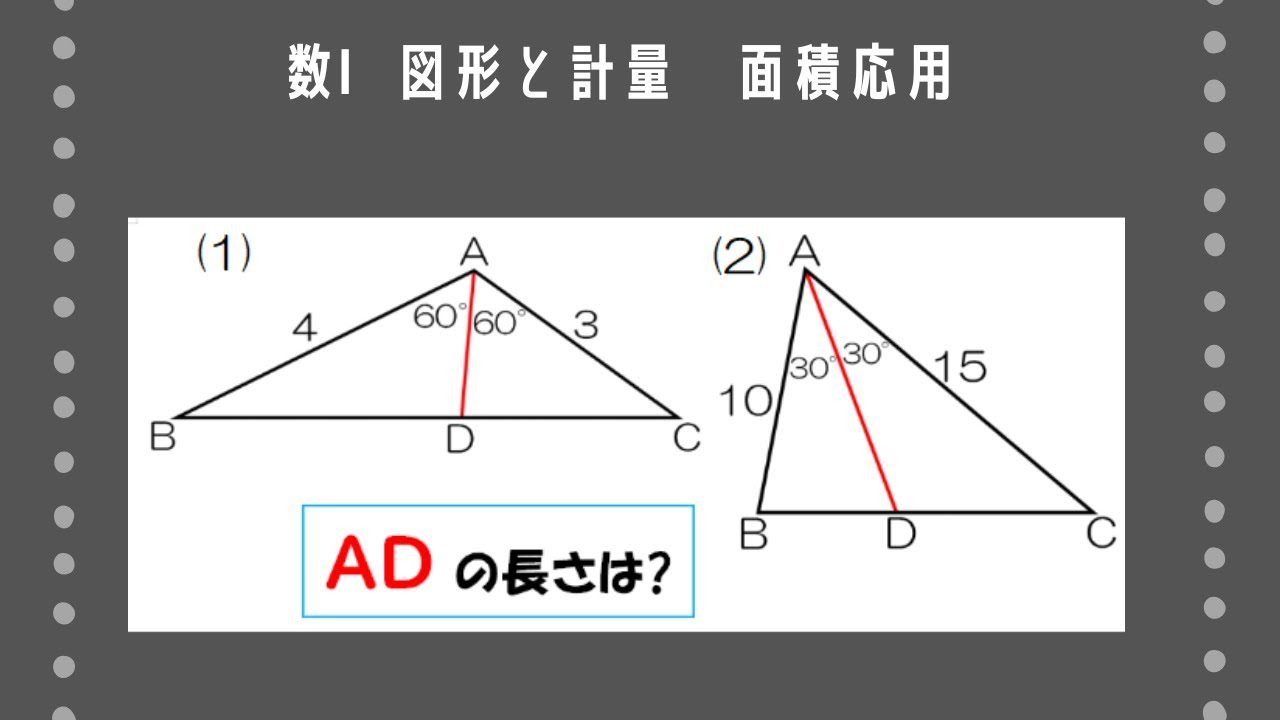
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
この動画を見る
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
【数Ⅰ】【図形と計量】面積応用7 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
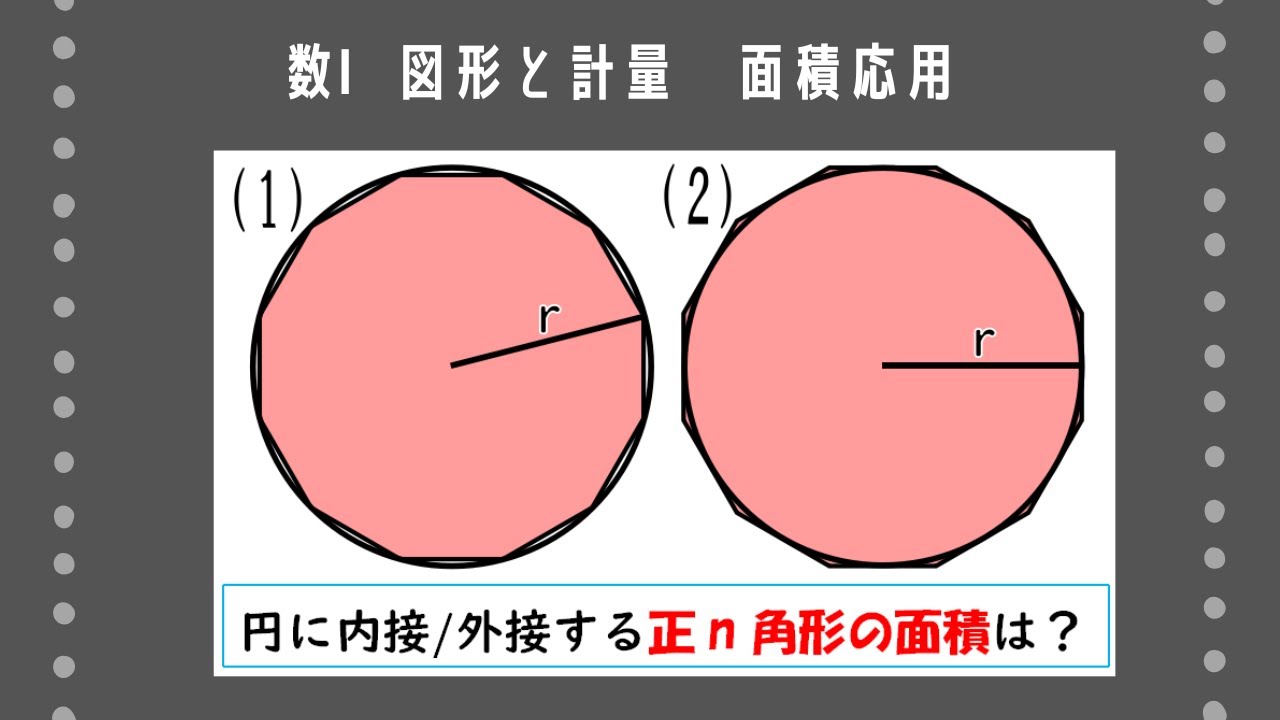
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
この動画を見る
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
【数Ⅰ】【図形と計量】面積応用6 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
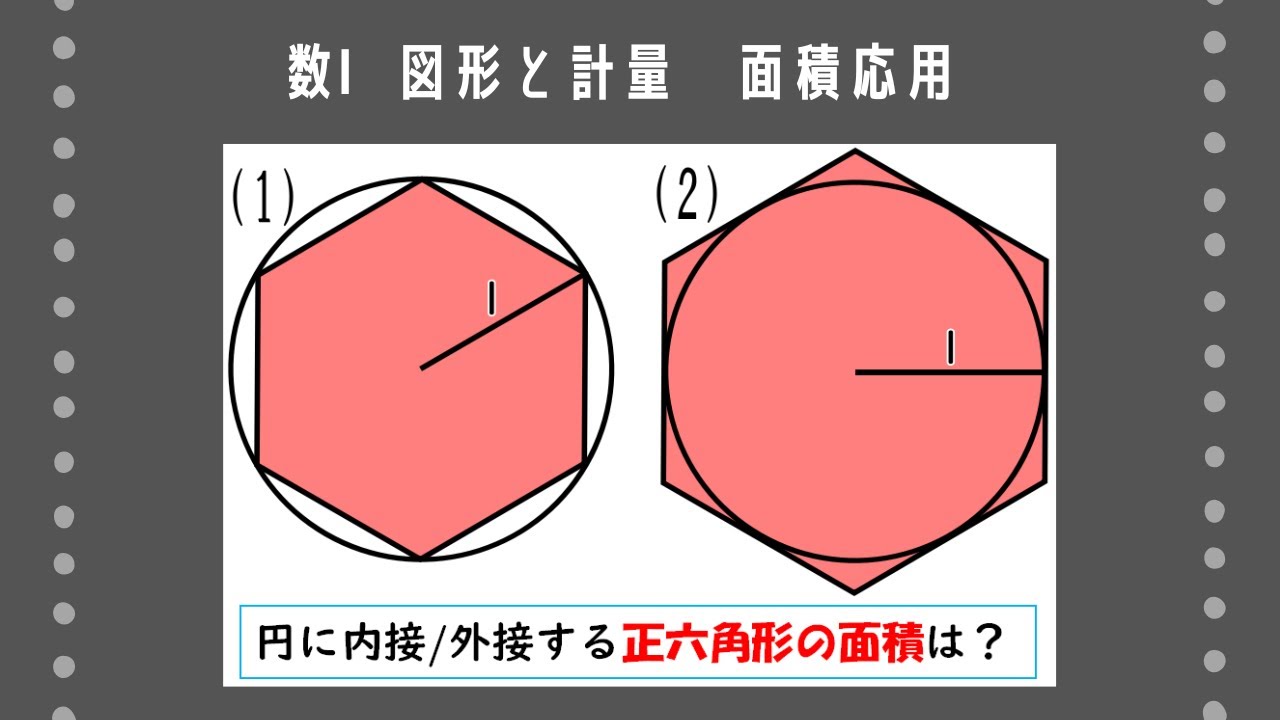
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
この動画を見る
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
【数Ⅰ】【図形と計量】面積応用5 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
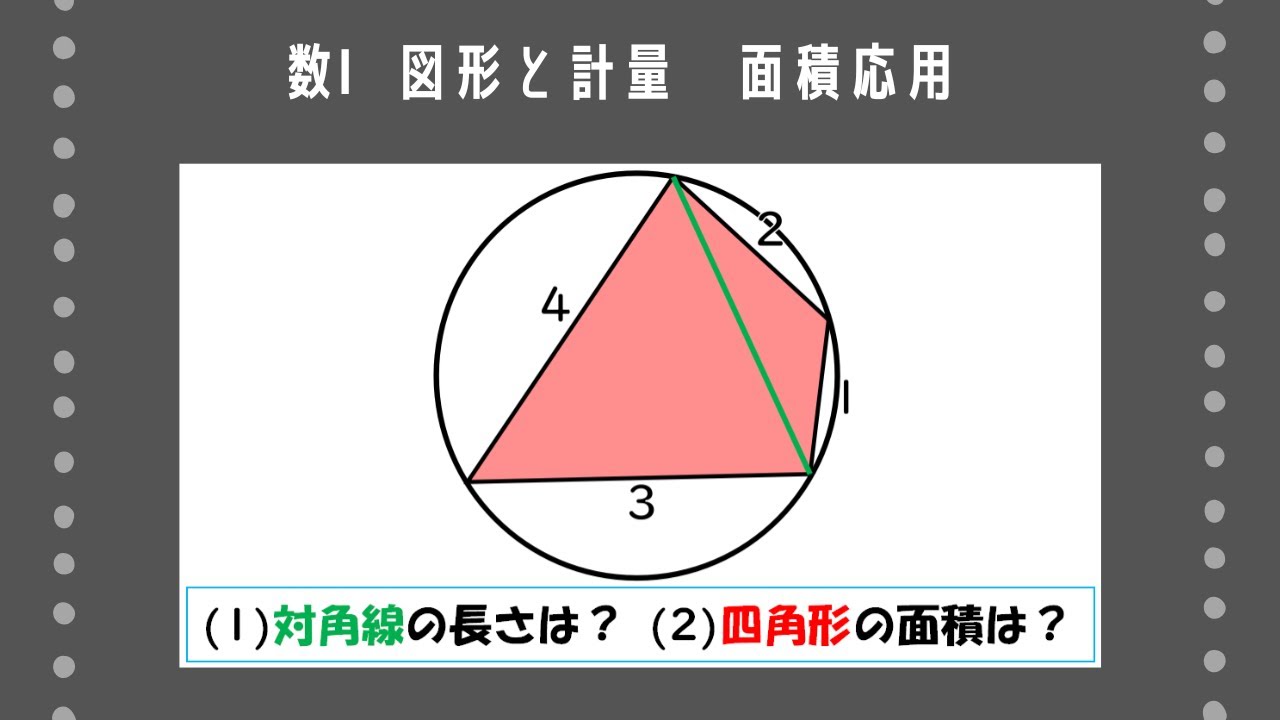
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
この動画を見る
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
【数Ⅰ】【図形と計量】面積応用4 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
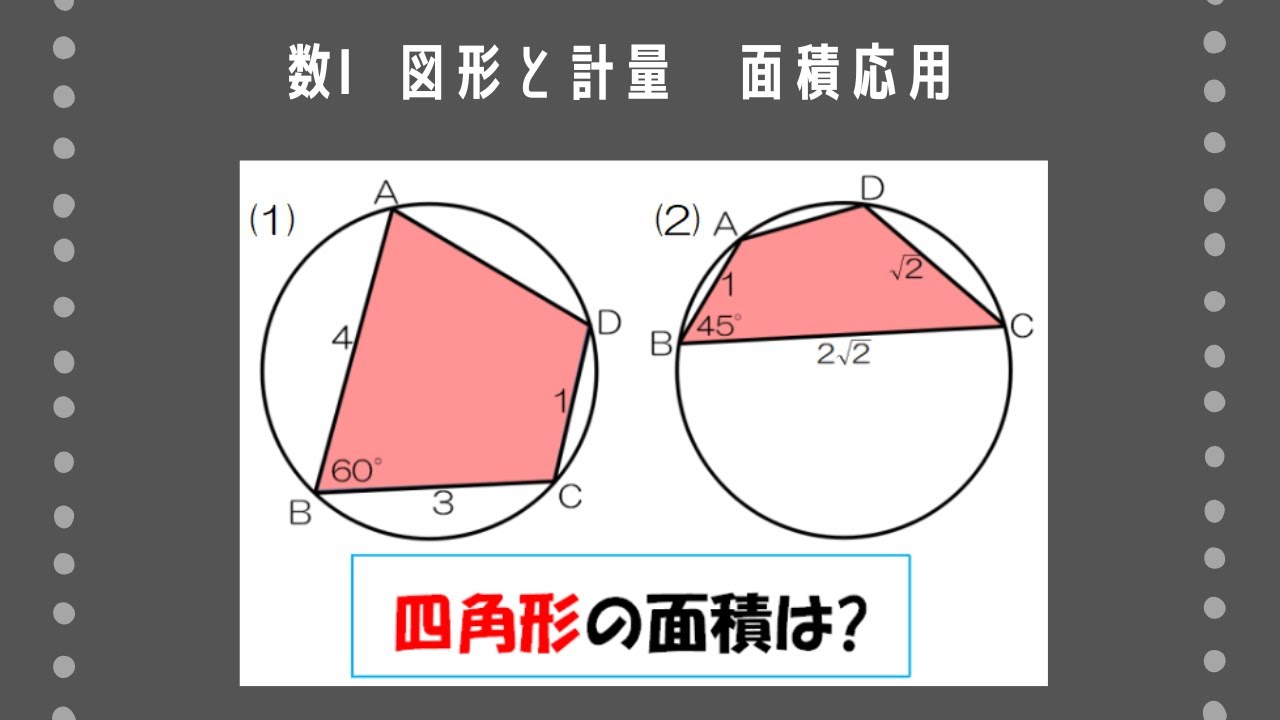
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
この動画を見る
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
【数Ⅰ】【図形と計量】面積応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
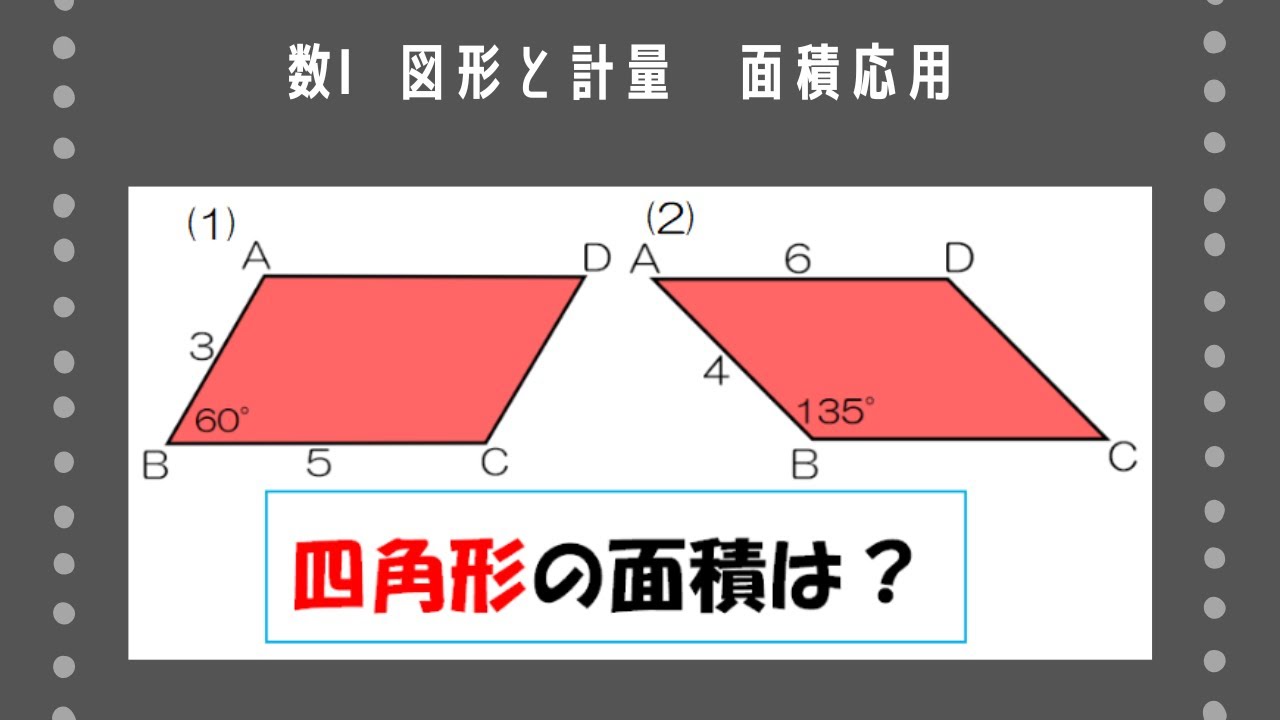
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
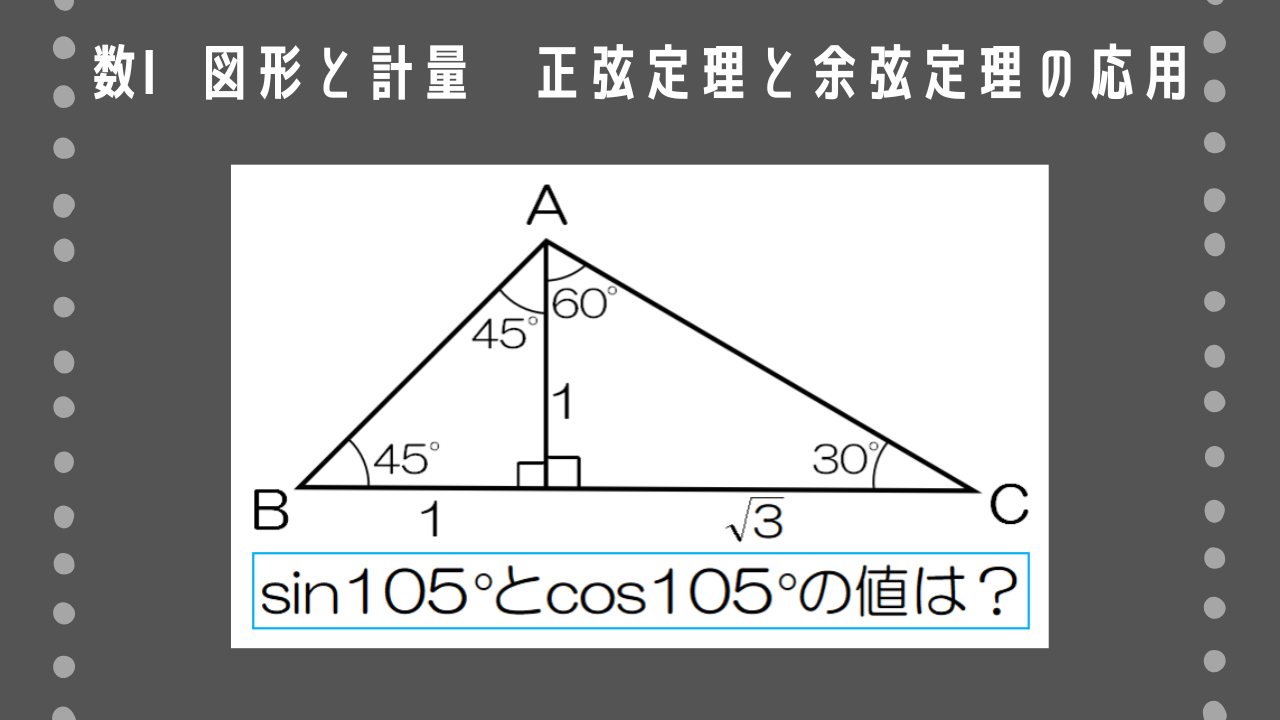
図を利用して、sin105°とcos105°の値を求めよ。
この動画を見る
図を利用して、sin105°とcos105°の値を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
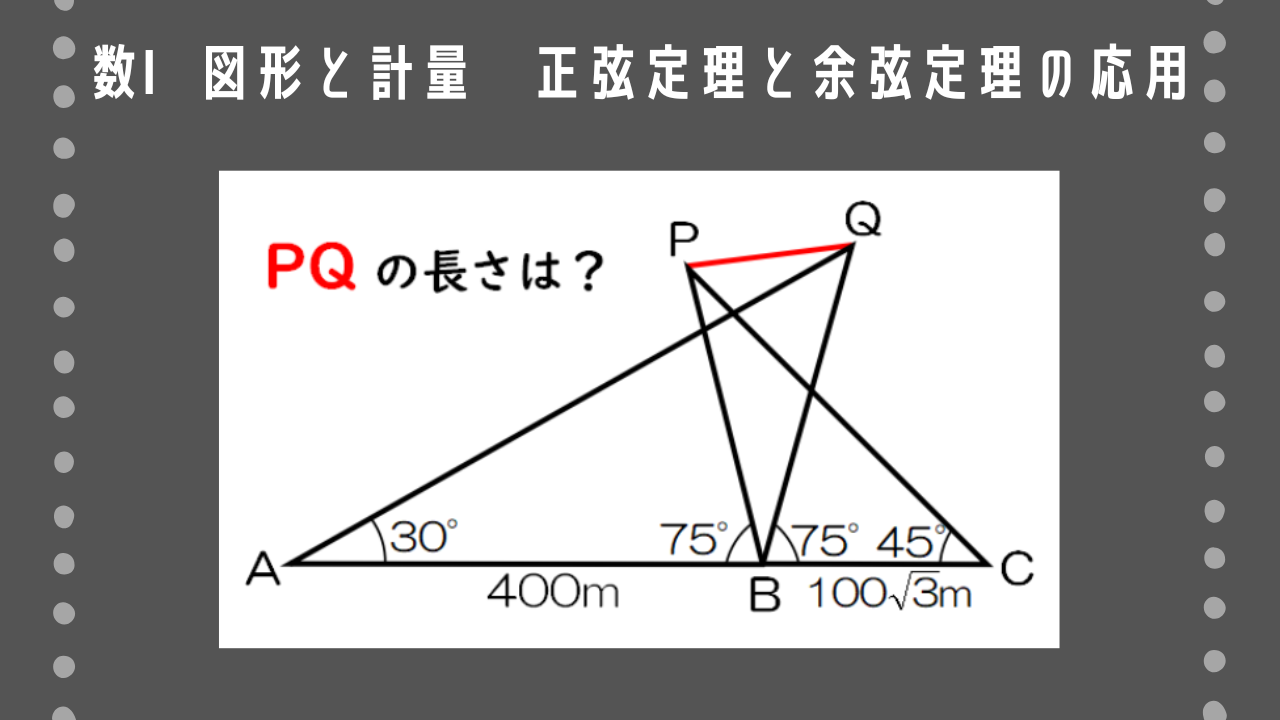
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
この動画を見る
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
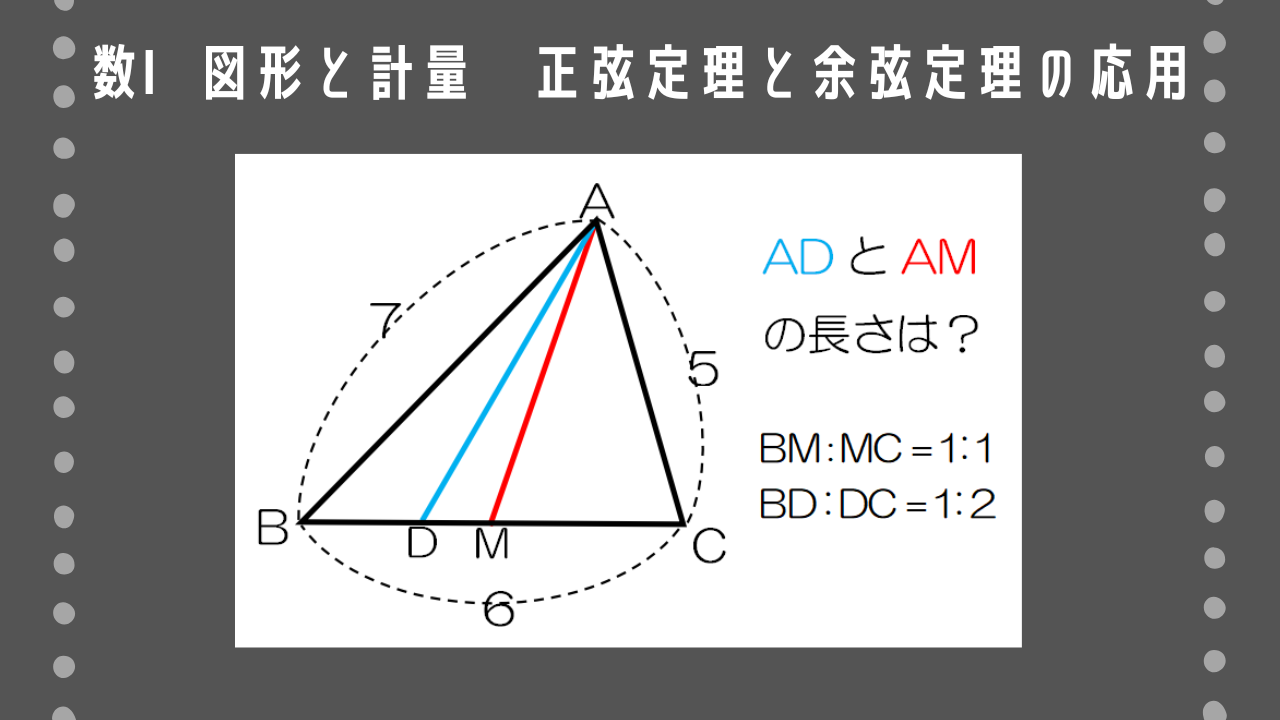
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
この動画を見る
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
【解法は1つでない…！】連立方程式：東京工業大学附属科学技術高等学校～全国入試問題解法
福田のおもしろ数学400〜2項展開の係数と次数に関する個数
単元：
#数Ⅰ#数A#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか？
この動画を見る
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか？
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数Ⅰ#数A#図形の性質#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\angle{B}=45^{ \circ }$
$\angle{C}=15^{ \circ }$
$AC=2\sqrt{3}+2 \triangle{ABC}の面積を求めなさい$
この動画を見る
$\angle{B}=45^{ \circ }$
$\angle{C}=15^{ \circ }$
$AC=2\sqrt{3}+2 \triangle{ABC}の面積を求めなさい$