 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
息抜き雑問

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
①$\sqrt{3・5・17・257+1}$
どちらが大きいか?
②$9^{12}$ VS $127^{5}$
この動画を見る
これを解け.
①$\sqrt{3・5・17・257+1}$
どちらが大きいか?
②$9^{12}$ VS $127^{5}$
福田のわかった数学〜高校1年生039〜15°の三角比

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$
15°の三角比
$\sin15°,\cos15°,\tan15°$を求めよ。
この動画を見る
数学$\textrm{I}$
15°の三角比
$\sin15°,\cos15°,\tan15°$を求めよ。
総復習
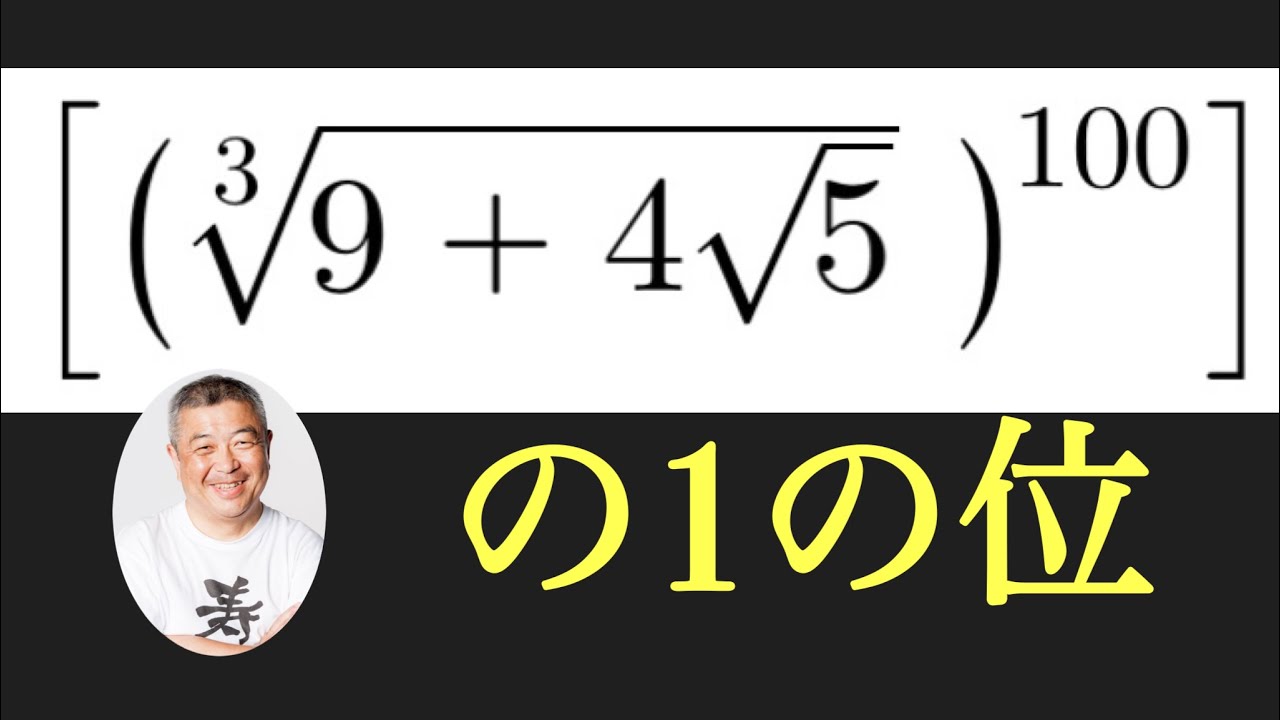
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(\sqrt[3]{9+4\sqrt5})^{100}]$の1の位を求めよ.
この動画を見る
$[(\sqrt[3]{9+4\sqrt5})^{100}]$の1の位を求めよ.
福田のわかった数学〜高校1年生037〜部屋割り論法(2)の訂正版

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 部屋割り論法(2)
座標平面上に異なる5個の格子点がある。これら5個の格子点の中に、
結んだ線分の中点がまた格子点となるような2点が存在することを示せ。
この動画を見る
数学$\textrm{I}$ 部屋割り論法(2)
座標平面上に異なる5個の格子点がある。これら5個の格子点の中に、
結んだ線分の中点がまた格子点となるような2点が存在することを示せ。
【中学数学】平方根・ルートの計算演習~乗法公式3~ 2-9.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})$
2⃣
$(5\sqrt{5}-2\sqrt{7})(5\sqrt{5}+2\sqrt{7})$
3⃣
$(\sqrt{3}+4)(\sqrt{3}-4)$
この動画を見る
1⃣
$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})$
2⃣
$(5\sqrt{5}-2\sqrt{7})(5\sqrt{5}+2\sqrt{7})$
3⃣
$(\sqrt{3}+4)(\sqrt{3}-4)$
福田のわかった数学〜高校1年生038〜三角比、簡単な測量
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
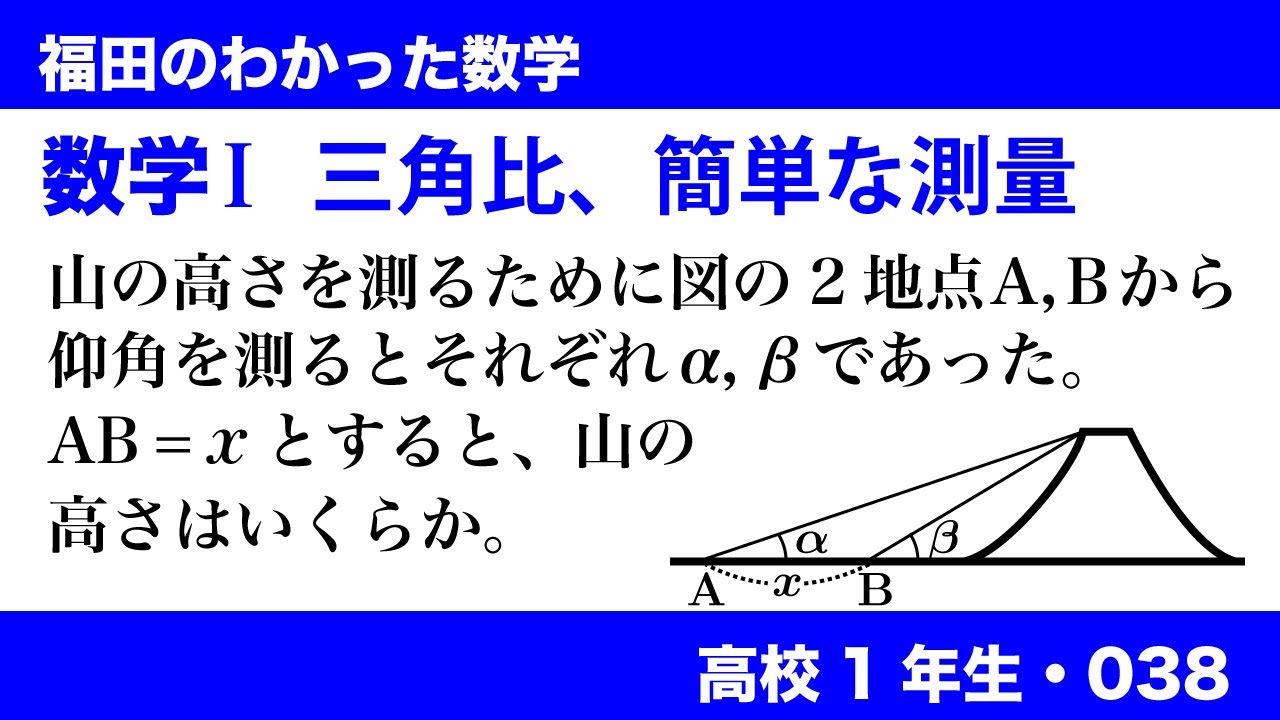
数学$\textrm{I}$三角比、簡単な測量
山の高さを測るために図の2地点A,B(※動画参照)から
仰角を測るとそれぞれ$\alpha,\beta$であった。
$AB=x$とすると、山の高さはいくらか。
この動画を見る
数学$\textrm{I}$三角比、簡単な測量
山の高さを測るために図の2地点A,B(※動画参照)から
仰角を測るとそれぞれ$\alpha,\beta$であった。
$AB=x$とすると、山の高さはいくらか。
ゆる言語学者バーゼル問題に驚く

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
バーゼル問題に関して解説していきます.
この動画を見る
バーゼル問題に関して解説していきます.
【中学数学】平方根・ルートの計算演習~乗法公式2~ 2-9.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(\sqrt{5}-\sqrt{2})^2$
2⃣
$(\sqrt{3}-5)^2$
3⃣
$(\sqrt{3}+3\sqrt{5})^2$
この動画を見る
1⃣
$(\sqrt{5}-\sqrt{2})^2$
2⃣
$(\sqrt{3}-5)^2$
3⃣
$(\sqrt{3}+3\sqrt{5})^2$
福田のわかった数学〜高校1年生037〜部屋割り論法(2)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{I} 部屋割り論法(2)\\
座標平面上で異なる5個の格子点の\\
どれか2個を結ぶと、その中点が格子点になることを証明せよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} 部屋割り論法(2)\\
座標平面上で異なる5個の格子点の\\
どれか2個を結ぶと、その中点が格子点になることを証明せよ。
\end{eqnarray}
福田の数学〜慶應義塾大学2021年経済学部第1問〜2つの円に同時に外接する円の条件

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
どっちがでかい?あれを証明します。

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$51^{100}$ VS $100!$
この動画を見る
どちらが大きいか?
$51^{100}$ VS $100!$
場合分けたくさん!

【中学数学】平方根・ルートの計算演習~乗法公式1~ 2-9【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(\sqrt{5}+3)(\sqrt{5}-2)$
2⃣
$(\sqrt{2}+3)(\sqrt{2}-1)$
3⃣
$(3\sqrt{5}-3)(6+3\sqrt{5})$
この動画を見る
1⃣
$(\sqrt{5}+3)(\sqrt{5}-2)$
2⃣
$(\sqrt{2}+3)(\sqrt{2}-1)$
3⃣
$(3\sqrt{5}-3)(6+3\sqrt{5})$
【中学数学】平方根・ルートの近似値の問題演習~解き方伝授~ 2-8【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{2}=1.41,\sqrt{5}=2.23$として次の値を求めよ
(1)$\sqrt{200}$
(2)$\sqrt{0.02}$
(3)$\sqrt{0.2}$
この動画を見る
$\sqrt{2}=1.41,\sqrt{5}=2.23$として次の値を求めよ
(1)$\sqrt{200}$
(2)$\sqrt{0.02}$
(3)$\sqrt{0.2}$
平方根の計算 工夫せよ 久留米大附設

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$
久留米大附設高等学校
この動画を見る
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$
久留米大附設高等学校
福田の数学〜慶應義塾大学2021年環境情報学部第4問〜条件を満たす部分集合の個数

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\scriptsize$ ${\Large\boxed{4}}$ $A_n=\left\{1,2,\ldots,n\right\}$を、$1$から$n$までの自然数の集合とする。$S$を$A_n$の部分集合(空集合および$A_n$自身も含む)としたとき、$S'$を$S$の要素それぞれに$1$を加えてできた集合とする。また$S''$を$S'$の要素それぞれにさらに$1$を加えてできた集合とする。たとえば、$A_3=\left\{1,2,3\right\}$の部分集合$S=\left\{1,3\right\}$の場合、$S'=\left\{2,4\right\},S''=\left\{3,5\right\}$
$(1)A_4=\left\{1,2,3,4\right\}$の部分集合$S=\left\{1,2,3\right\}$は$S \cup S'=A_4$となる。このように$A_4$の部分集合で$S \cup S'=A_4$となるものは$\left\{1,2,3\right\}$と$\left\{1,\boxed{\ \ ア\ \ }\right\}$の$2つ$である。
$(2)$$A_n$の$部分集合S$で$S \cup S'=A_n$となるような$S$の個数を$a_n$とすると、$(1)$から分かるように$a_4=2$であり$a_5=\boxed{\ \ イウ\ \ },$ $a_6=\boxed{\ \ エオ\ \ },$$a_7=\boxed{\ \ カキ\ \ },$$a_8=\boxed{\ \ クケ\ \ },$$\ldots,a_{16}=\boxed{\ \ コサシ\ \ }$となる。
$(3)$$A_4=\left\{1,2,3,4\right\}$の$部分集合S$で$S\cup S''=A_4$となるものは$S=\left\{1,\boxed{\ \ ス\ \ }\right\}$だけである。
$(4)A_n$の$部分集合S$で$S \cup S''=A_n$となるような$S$の個数を$b_n$とすると、$(3)$から分かるように$b_4=1$であり$ b_5=\boxed{\ \ セソ\ \ },$$b_6=\boxed{\ \ タチ\ \ },$$b_7=\boxed{\ \ ツテ\ \ },$$b_8=\boxed{\ \ トナ\ \ },$$\ldots,b_{16}=\boxed{\ \ ニヌネ\ \ }$となる。
2021慶應義塾大学環境情報学部過去問
この動画を見る
$\scriptsize$ ${\Large\boxed{4}}$ $A_n=\left\{1,2,\ldots,n\right\}$を、$1$から$n$までの自然数の集合とする。$S$を$A_n$の部分集合(空集合および$A_n$自身も含む)としたとき、$S'$を$S$の要素それぞれに$1$を加えてできた集合とする。また$S''$を$S'$の要素それぞれにさらに$1$を加えてできた集合とする。たとえば、$A_3=\left\{1,2,3\right\}$の部分集合$S=\left\{1,3\right\}$の場合、$S'=\left\{2,4\right\},S''=\left\{3,5\right\}$
$(1)A_4=\left\{1,2,3,4\right\}$の部分集合$S=\left\{1,2,3\right\}$は$S \cup S'=A_4$となる。このように$A_4$の部分集合で$S \cup S'=A_4$となるものは$\left\{1,2,3\right\}$と$\left\{1,\boxed{\ \ ア\ \ }\right\}$の$2つ$である。
$(2)$$A_n$の$部分集合S$で$S \cup S'=A_n$となるような$S$の個数を$a_n$とすると、$(1)$から分かるように$a_4=2$であり$a_5=\boxed{\ \ イウ\ \ },$ $a_6=\boxed{\ \ エオ\ \ },$$a_7=\boxed{\ \ カキ\ \ },$$a_8=\boxed{\ \ クケ\ \ },$$\ldots,a_{16}=\boxed{\ \ コサシ\ \ }$となる。
$(3)$$A_4=\left\{1,2,3,4\right\}$の$部分集合S$で$S\cup S''=A_4$となるものは$S=\left\{1,\boxed{\ \ ス\ \ }\right\}$だけである。
$(4)A_n$の$部分集合S$で$S \cup S''=A_n$となるような$S$の個数を$b_n$とすると、$(3)$から分かるように$b_4=1$であり$ b_5=\boxed{\ \ セソ\ \ },$$b_6=\boxed{\ \ タチ\ \ },$$b_7=\boxed{\ \ ツテ\ \ },$$b_8=\boxed{\ \ トナ\ \ },$$\ldots,b_{16}=\boxed{\ \ ニヌネ\ \ }$となる。
2021慶應義塾大学環境情報学部過去問
【裏技】平方根・ルートの近似値の出し方~面白テクニック~

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
平方根・ルートの近似値の出し方紹介動画です
この動画を見る
平方根・ルートの近似値の出し方紹介動画です
6乗根 一橋の類題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt[6]{99+70\sqrt2}$
$\beta=\sqrt[6]{99-70\sqrt2}$
$Am=\alpha^{2n-1}-\beta^{2n-1}$
$n$が自然数のとき,$An$は整数であることを示せ.
この動画を見る
$\alpha=\sqrt[6]{99+70\sqrt2}$
$\beta=\sqrt[6]{99-70\sqrt2}$
$Am=\alpha^{2n-1}-\beta^{2n-1}$
$n$が自然数のとき,$An$は整数であることを示せ.
【中学数学】平方根・ルートの色々な計算~代入する問題~ 2-7【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$
2⃣
$x^2+2xy+y^2$
この動画を見る
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$
2⃣
$x^2+2xy+y^2$
福田の数学〜慶應義塾大学2021年環境情報学部第1問〜三角形の内部にある外接している5つの円
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#方べきの定理と2つの円の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
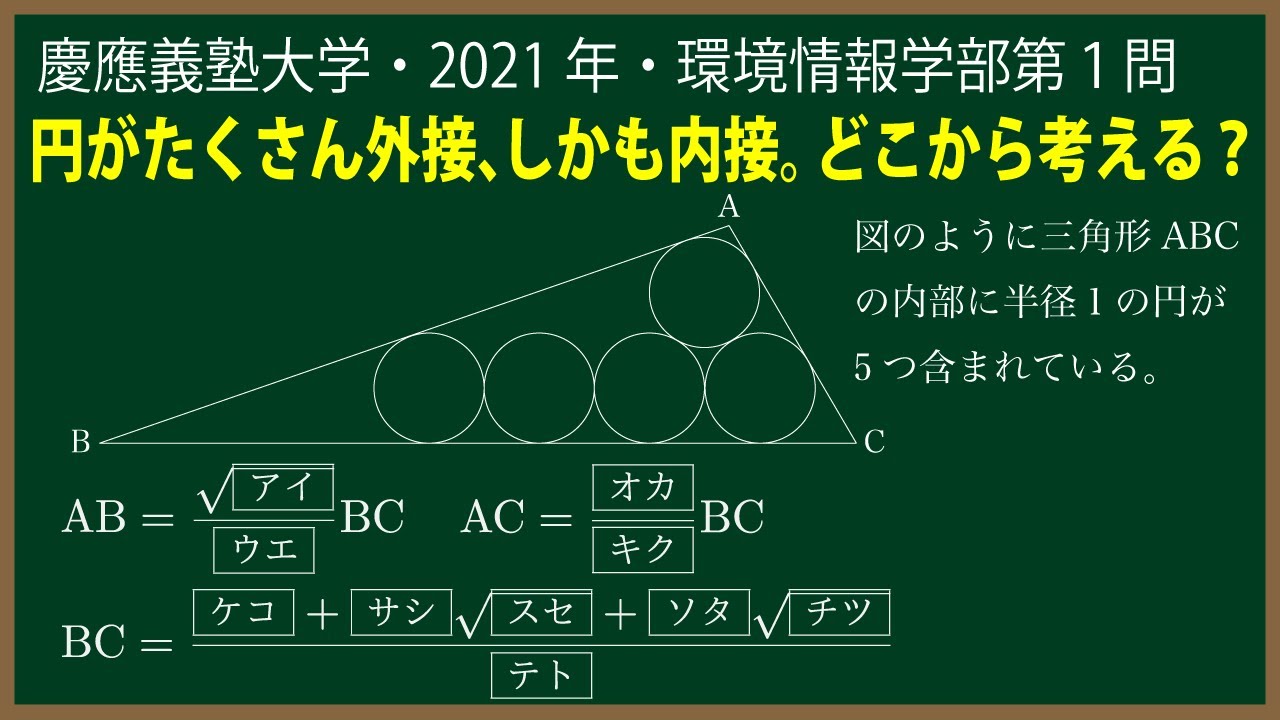
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$ $(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。
2021慶應義塾大学環境情報学部過去問
この動画を見る
${\Large\boxed{1}}$
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$ $(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。
2021慶應義塾大学環境情報学部過去問
福田のわかった数学〜高校1年生035〜必要条件・十分条件

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 必要条件・十分条件
$a \gt 0$とする。2つの条件$p,q$を
$p:|x-1| \leqq a, q:|x| \lt 2$とする。
(1)$p$が$q$の十分条件となる$a$の範囲
(2)$p$が$q$の必要条件となる$a$の範囲
この動画を見る
数学$\textrm{I}$ 必要条件・十分条件
$a \gt 0$とする。2つの条件$p,q$を
$p:|x-1| \leqq a, q:|x| \lt 2$とする。
(1)$p$が$q$の十分条件となる$a$の範囲
(2)$p$が$q$の必要条件となる$a$の範囲
1の5乗根の計算
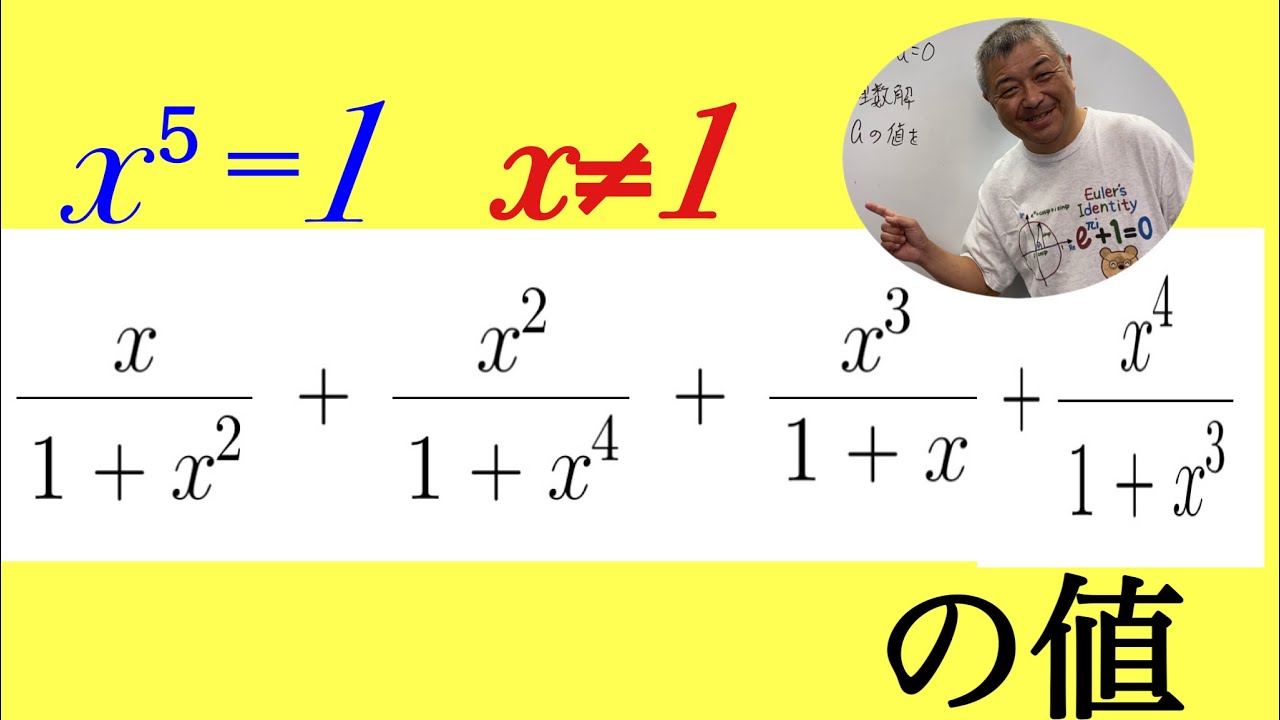
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^5=1,x \neq 1$である.
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
この動画を見る
$x^5=1,x \neq 1$である.
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
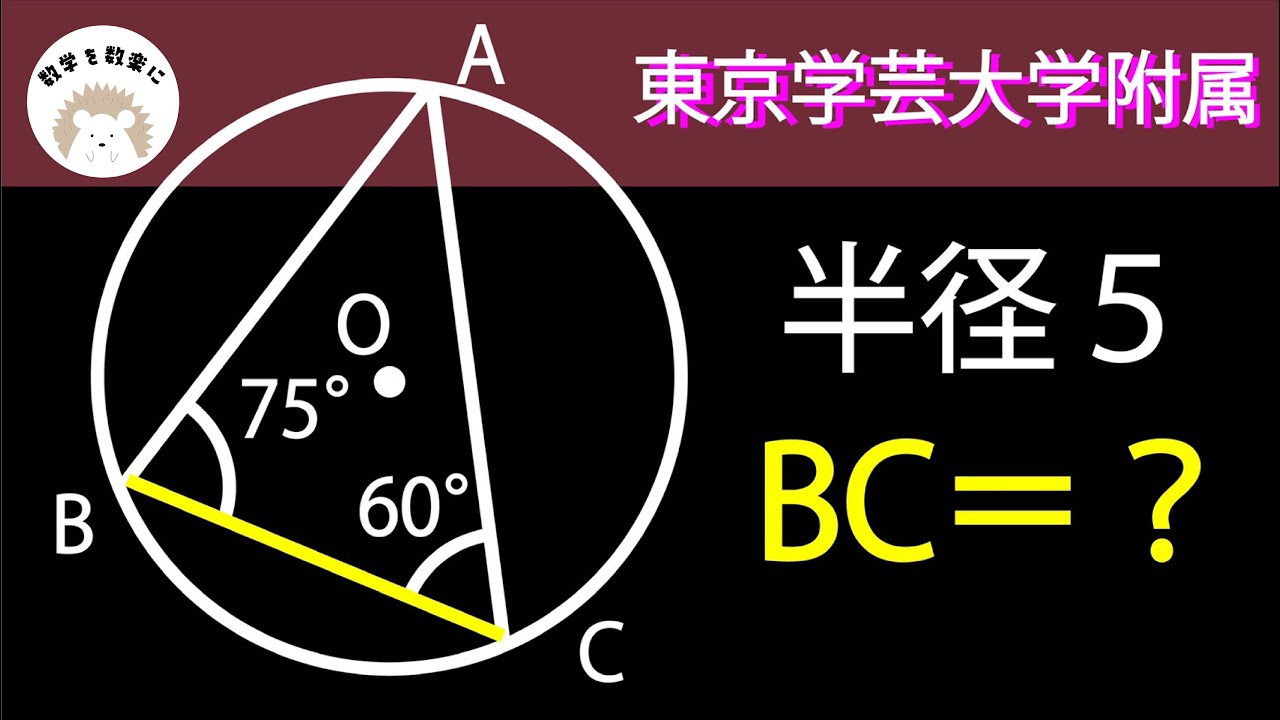
円 東京学芸大学附属
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
【2次不等式は図で解く!】2次不等式を2次関数でイメージする方法を解説!【高校数学 数学】

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
(1)$x^2+3x-4 \lt 0$
(2)$-x^2-2x+4 \geqq 0$
この動画を見る
(1)$x^2+3x-4 \lt 0$
(2)$-x^2-2x+4 \geqq 0$
福田の数学〜慶應義塾大学2021年医学部第2問〜データの分析、共分散と相関係数

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
$n$人のクラス(ただし$n \gt 1$)で英語と理科のテストを実施する。ただしどちらの科目にも同順位の者はいないとする。出席番号$i(i=1,2,\ldots,n)$の生徒について、その英語の順位$x$と理科の順位$y$の組を$(x_i,y_i)$で表す。
(1)変量$x$の平均値$\bar{ x }$と分散$s_x^2$をそれぞれ求めると$\bar{ x }=\boxed{\ \ (あ)\ \ },s_x^2=\boxed{\ \ (い)\ \ }$である。
(2)変量$x,y$の共分散$s_{xy}$とする。クラスの人数$n$が奇数の2倍であるとき、$s_{xy}\neq 0$であることを示しなさい。
(3)$i=1,2,\ldots,n$に対して$d_i=x_i-y_i$とおく。変量$x,y$の相関係数を$r$とするとき、$r$は$n$と$d_1,d_2,\ldots,d_n$を用いて$r=1-\dfrac{6}{\boxed{\ \ (う)\ \ }}\boxed{\ \ (え)\ \ }$と表される。
(4)$x_i$と$y_i$の間に$y_i=\boxed{\ \ (お)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最大値$\boxed{\ \ (か)\ \ }$をとり$y_i=\boxed{\ \ (き)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最小値$\boxed{\ \ (く)\ \ }$をとる。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{2}}$
$n$人のクラス(ただし$n \gt 1$)で英語と理科のテストを実施する。ただしどちらの科目にも同順位の者はいないとする。出席番号$i(i=1,2,\ldots,n)$の生徒について、その英語の順位$x$と理科の順位$y$の組を$(x_i,y_i)$で表す。
(1)変量$x$の平均値$\bar{ x }$と分散$s_x^2$をそれぞれ求めると$\bar{ x }=\boxed{\ \ (あ)\ \ },s_x^2=\boxed{\ \ (い)\ \ }$である。
(2)変量$x,y$の共分散$s_{xy}$とする。クラスの人数$n$が奇数の2倍であるとき、$s_{xy}\neq 0$であることを示しなさい。
(3)$i=1,2,\ldots,n$に対して$d_i=x_i-y_i$とおく。変量$x,y$の相関係数を$r$とするとき、$r$は$n$と$d_1,d_2,\ldots,d_n$を用いて$r=1-\dfrac{6}{\boxed{\ \ (う)\ \ }}\boxed{\ \ (え)\ \ }$と表される。
(4)$x_i$と$y_i$の間に$y_i=\boxed{\ \ (お)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最大値$\boxed{\ \ (か)\ \ }$をとり$y_i=\boxed{\ \ (き)\ \ }(i=1,2,\ldots,n)$の関係があるとき$r$は最小値$\boxed{\ \ (く)\ \ }$をとる。
2021慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2021年医学部第1問(3)〜集合の要素の個数と2次方程式の解

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#複素数と方程式#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#複素数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(3)整数$k$に対して、$x$の2次方程式$x^2+kx+k+35=0$の解を$\alpha_k,\beta_k$とおく。
ただし、方程式が重解をもつときは$\alpha_k=\beta_k$である。また$U=\left\{k|kは整数、かつ|k| \leqq 100 \right\}$を全体集合とし、その部分集合$A=\{k|k \in U$かつ$\alpha_k,\beta_k$はともに実数で$\alpha_k\neq \beta_k\}$
$B=\{k|k \in U$かつ$\alpha_k,\beta_k$の実数はともに2より大きい$\}$
$C=\{k|k \in U$かつ$\alpha_k,\beta_k$の実部と虚部はすべて整数$\}$
を考える。このとき$n(A)=\boxed{\ \ (か)\ \ },$$n(A \cap B)=\boxed{\ \ (き)\ \ },$$n(\bar{ A } \cap B)=\boxed{\ \ (く)\ \ },$
$n(A \cap C)=\boxed{\ \ (け)\ \ },$$n(\bar{ A } \cap C)=\boxed{\ \ (こ)\ \ }$である。ただし有限集合$X$に対してその要素の個数を$n(X)$で表す。また$\bar{ A }$は$A$の補集合である。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{1}}$
(3)整数$k$に対して、$x$の2次方程式$x^2+kx+k+35=0$の解を$\alpha_k,\beta_k$とおく。
ただし、方程式が重解をもつときは$\alpha_k=\beta_k$である。また$U=\left\{k|kは整数、かつ|k| \leqq 100 \right\}$を全体集合とし、その部分集合$A=\{k|k \in U$かつ$\alpha_k,\beta_k$はともに実数で$\alpha_k\neq \beta_k\}$
$B=\{k|k \in U$かつ$\alpha_k,\beta_k$の実数はともに2より大きい$\}$
$C=\{k|k \in U$かつ$\alpha_k,\beta_k$の実部と虚部はすべて整数$\}$
を考える。このとき$n(A)=\boxed{\ \ (か)\ \ },$$n(A \cap B)=\boxed{\ \ (き)\ \ },$$n(\bar{ A } \cap B)=\boxed{\ \ (く)\ \ },$
$n(A \cap C)=\boxed{\ \ (け)\ \ },$$n(\bar{ A } \cap C)=\boxed{\ \ (こ)\ \ }$である。ただし有限集合$X$に対してその要素の個数を$n(X)$で表す。また$\bar{ A }$は$A$の補集合である。
2021慶應義塾大学医学部過去問
福田のわかった数学〜高校1年生034〜背理法(2)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 背理法(2)
$\sqrt2,\sqrt[3]3$が無理数であることを既知として次を証明せよ。
$p,q,\sqrt2p+\sqrt[3]3q$が全て有理数 $\Rightarrow p=q=0$
この動画を見る
数学$\textrm{I}$ 背理法(2)
$\sqrt2,\sqrt[3]3$が無理数であることを既知として次を証明せよ。
$p,q,\sqrt2p+\sqrt[3]3q$が全て有理数 $\Rightarrow p=q=0$
トルコJr数学オリンピック

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$(x,y)$を求めよ.
$2x^2+y^2+7=2(x+1)(y+1)$
トルコJr数学オリンピック
この動画を見る
実数解$(x,y)$を求めよ.
$2x^2+y^2+7=2(x+1)(y+1)$
トルコJr数学オリンピック
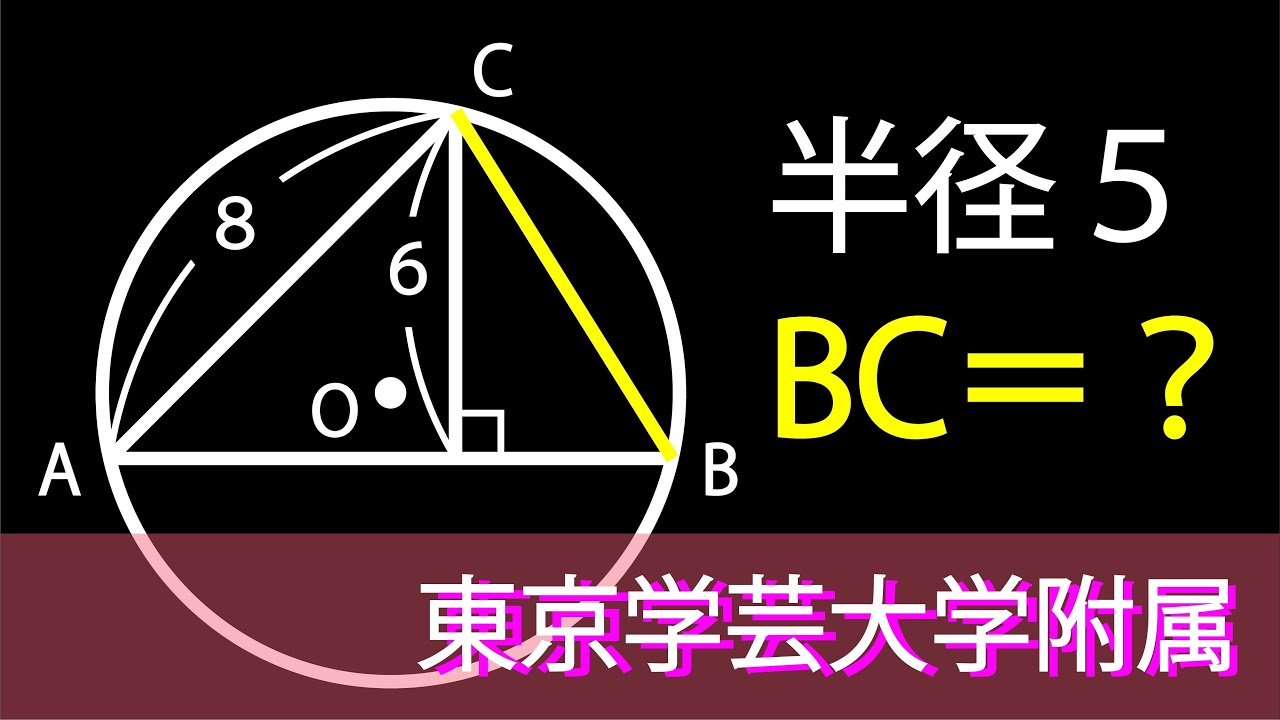
円と直角三角形 B
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
【中学数学】平方根・ルートの整数部分・小数部分を求める問題 2-6【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
この動画を見る
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
