数Ⅰ
数Ⅰ
【数Ⅰ】【図形と計量】有名角以外を含む三角比の計算 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の式の値を求めよ。
(1) $\sin^2 40°+\sin^2 50°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^2 50°$
この動画を見る
次の式の値を求めよ。
(1) $\sin^2 40°+\sin^2 50°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^2 50°$
【数Ⅰ】【データの分析】変量変換1 ※問題文は概要欄
単元：
#数Ⅰ#データの分析#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
変量xのデータの平均値$\bar{x}$が35、分散$S_{x}^2$が16であるとする。この時、次の式によって得られる新しい変量yのデータについて、平均$\bar{y}$，分散$S_{y}^2$，標準偏差$S_{y}$を求めよ。
（１）$y=x-10$
（２）$y=3x$
（３）$y=-\frac{1}{2}x+6$
あるクラスの生徒を対象に100点満点の試験を行ったところ，平均値は68点，分散は36であった。得点調整のため，生徒全員の得点を2.5倍して，更に30点を加えたとき，得点調整後の平均値，分散，標準偏差を求めよ。
この動画を見る
変量xのデータの平均値$\bar{x}$が35、分散$S_{x}^2$が16であるとする。この時、次の式によって得られる新しい変量yのデータについて、平均$\bar{y}$，分散$S_{y}^2$，標準偏差$S_{y}$を求めよ。
（１）$y=x-10$
（２）$y=3x$
（３）$y=-\frac{1}{2}x+6$
あるクラスの生徒を対象に100点満点の試験を行ったところ，平均値は68点，分散は36であった。得点調整のため，生徒全員の得点を2.5倍して，更に30点を加えたとき，得点調整後の平均値，分散，標準偏差を求めよ。
【数Ⅰ】【データの分析】変量変換2 ※問題文は概要欄
単元：
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
変量$\mathit{x}$のデータが次のように与えられている。
672, 693, 644, 665, 630, 644
$\mathit{c}=7 , \mathit{x}_{0}=644 ,\mathit{u}=\frac{x-x₀}{c}$として新たな変量$\mathit{u}$を作る。
（１）変量$\mathit{u}$のデータの平均値、分散、標準偏差を求めよ。
（２）変量$\mathit{x}$のデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量$\mathit{x}$のデータが次のように与えられている。
672, 693, 644, 665, 630, 644
$\mathit{c}=7 , \mathit{x}_{0}=644 ,\mathit{u}=\frac{x-x₀}{c}$として新たな変量$\mathit{u}$を作る。
（１）変量$\mathit{u}$のデータの平均値、分散、標準偏差を求めよ。
（２）変量$\mathit{x}$のデータの平均値、分散、標準偏差を求めよ。
【数Ⅰ】【データの分析】平均と分散だけ与えられたデータ ※問題文は概要欄
単元：
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
20個の値からなるデータがあり、そのうちの8個の値の平均値は３，分散は４、残りの12個の値の平均値は8、分散は9である。
（１）このデータの平均値を求めよ。
（２）このデータの分散を求めよ
この動画を見る
20個の値からなるデータがあり、そのうちの8個の値の平均値は３，分散は４、残りの12個の値の平均値は8、分散は9である。
（１）このデータの平均値を求めよ。
（２）このデータの分散を求めよ
【数Ⅰ】【データの分析】データが変更されたときの平均、分散の関係 ※問題文は概要欄
単元：
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9（単位は回）
（１） このデータの平均値を求めよ。
（２） このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
（３）（２）の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
この動画を見る
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9（単位は回）
（１） このデータの平均値を求めよ。
（２） このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
（３）（２）の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
100個の絶対値の合計！？どう解く？ #Shorts #ずんだもん #勉強
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
nが整数であるとき、S=｜n-1｜＋｜n-2｜＋・・・＋｜n-100｜の最小値を求めよ。
この動画を見る
nが整数であるとき、S=｜n-1｜＋｜n-2｜＋・・・＋｜n-100｜の最小値を求めよ。
【数Ⅰ】【2次関数】条件付きの解 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)２次関数$y=x^2+mx+1$において、$y$の値が常に正常である。
(2) 放物線$y=x^2+2mx+3m-2$が$y<0$の部分を通らない。
(3) 関数$y=mx^2+4x+m-3$において、$y$の値が常に負である。
２次関数$y=x^2-mx+m+3$のグラフの頂点が第１象限にあるとき、定数$m$の値の範囲を求めよ。
この動画を見る
次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)２次関数$y=x^2+mx+1$において、$y$の値が常に正常である。
(2) 放物線$y=x^2+2mx+3m-2$が$y<0$の部分を通らない。
(3) 関数$y=mx^2+4x+m-3$において、$y$の値が常に負である。
２次関数$y=x^2-mx+m+3$のグラフの頂点が第１象限にあるとき、定数$m$の値の範囲を求めよ。
【数Ⅰ】【2次関数】2次関数 解の個数、連立 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$m$は定数とする。放物線$y=x^2+(m+3)x+3m+4$と$x$軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数$m$の値の範囲を求めよ。
(1)$x^2-mx+1＞0$(2)$x^2+mx+2m\leqq0$
次の連立不等式を満たす整数$x$の値を全て求めよ。
\begin{eqnarray}
(1)\left\{
\begin{array}{l}
2x^2-x-3＜0\\
3x^2-10x+3＜0
\end{array}
\right.
(2)\left\{
\begin{array}{l}
x^2+2x>1\\
x^2-x\leqq6
\end{array}
\right.
\end{eqnarray}
この動画を見る
$m$は定数とする。放物線$y=x^2+(m+3)x+3m+4$と$x$軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数$m$の値の範囲を求めよ。
(1)$x^2-mx+1＞0$(2)$x^2+mx+2m\leqq0$
次の連立不等式を満たす整数$x$の値を全て求めよ。
\begin{eqnarray}
(1)\left\{
\begin{array}{l}
2x^2-x-3＜0\\
3x^2-10x+3＜0
\end{array}
\right.
(2)\left\{
\begin{array}{l}
x^2+2x>1\\
x^2-x\leqq6
\end{array}
\right.
\end{eqnarray}
【数Ⅰ】【2次関数】解の範囲 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題1
次の方程式が実数解をもつように、実数 $m$ の値の範囲を定めよ。
$(1)\, x^2+2mx+3=0$
$(2)\, x^2+mx+m=0$
問題2
2次方程式 $x^2-2mx-4m=0$ が次の条件を満たすように、定数 $m$ の値の範囲を定めよ。
$(1)$ 異なる2つの実数解をもつ
$(2)$ 実数解をもたない
問題3
次の条件を満たすように、実数 $m$ の値の範囲を定めよ。
$(1)$ 2次関数 $y=x^2-2mx+2m+3$ のグラフが $x$ 軸と共有点をもつ
$(2)$ 2次関数 $y=x^2+2mx-m+2$ のグラフが $x$ 軸と共有点をもたない
この動画を見る
問題1
次の方程式が実数解をもつように、実数 $m$ の値の範囲を定めよ。
$(1)\, x^2+2mx+3=0$
$(2)\, x^2+mx+m=0$
問題2
2次方程式 $x^2-2mx-4m=0$ が次の条件を満たすように、定数 $m$ の値の範囲を定めよ。
$(1)$ 異なる2つの実数解をもつ
$(2)$ 実数解をもたない
問題3
次の条件を満たすように、実数 $m$ の値の範囲を定めよ。
$(1)$ 2次関数 $y=x^2-2mx+2m+3$ のグラフが $x$ 軸と共有点をもつ
$(2)$ 2次関数 $y=x^2+2mx-m+2$ のグラフが $x$ 軸と共有点をもたない
【数Ⅰ】【2次関数】点の通過 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題1
次の条件を満たす放物線の方程式を求めよ。
$(1)$ 3点 $(-4,0), \, (-2,0), \, (0,-4)$ を通る。
$(2)$ 点 $(2,0)$ で $x$ 軸に接し、点 $(-2,12)$ を通る。
問題2
$a, \, b, \, c$ の値を入力すると、関数 $y=ax^2+bx+c$ のグラフが表示されるコンピュータソフトがある。ある $a, \, b, \, c$ の値を入力すると、グラフは図のように表示された (図は動画参照)。
$(1)$ $a, \, b, \, c, \, b^2-4ac, \, a+b+c$ の符号をいえ。
$(2)$ この $a, \, b$ の値を変えずに、$c$ の値だけを変化させたとき、変わらないものを次の中からすべて選べ。また、変わらない理由を説明せよ。
① グラフと $x$ 軸の共有点の個数
② グラフの頂点の $x$ 座標の符号
③ グラフの頂点の $y$ 座標の符号
この動画を見る
問題1
次の条件を満たす放物線の方程式を求めよ。
$(1)$ 3点 $(-4,0), \, (-2,0), \, (0,-4)$ を通る。
$(2)$ 点 $(2,0)$ で $x$ 軸に接し、点 $(-2,12)$ を通る。
問題2
$a, \, b, \, c$ の値を入力すると、関数 $y=ax^2+bx+c$ のグラフが表示されるコンピュータソフトがある。ある $a, \, b, \, c$ の値を入力すると、グラフは図のように表示された (図は動画参照)。
$(1)$ $a, \, b, \, c, \, b^2-4ac, \, a+b+c$ の符号をいえ。
$(2)$ この $a, \, b$ の値を変えずに、$c$ の値だけを変化させたとき、変わらないものを次の中からすべて選べ。また、変わらない理由を説明せよ。
① グラフと $x$ 軸の共有点の個数
② グラフの頂点の $x$ 座標の符号
③ グラフの頂点の $y$ 座標の符号
【数Ⅰ】【集合と論証】有理数、無理数の証明 ※問題文は概要欄
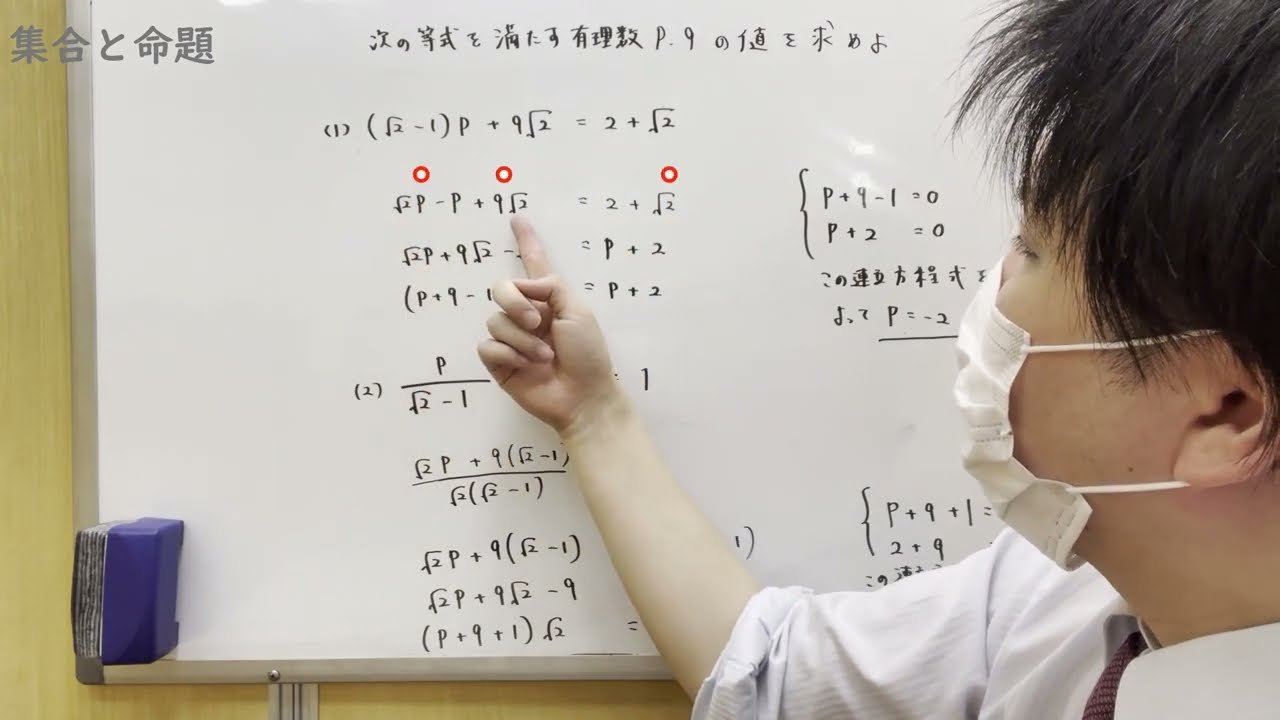
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題1
次の条件を満たす有理数 $p, \, q$ の値を求めよ。
$(1) \, (\sqrt{2}-1)p+q\sqrt(2)=2+\sqrt{2}$
$(2) \, \frac{p}{\sqrt{2}-1}+\frac{q}{\sqrt{2}}=1$
問題2
$p, \, q$ が有理数、$X$ が無理数で、$p+qX=0$ であるならば、$p=q=0$ であることを証明せよ。
この動画を見る
問題1
次の条件を満たす有理数 $p, \, q$ の値を求めよ。
$(1) \, (\sqrt{2}-1)p+q\sqrt(2)=2+\sqrt{2}$
$(2) \, \frac{p}{\sqrt{2}-1}+\frac{q}{\sqrt{2}}=1$
問題2
$p, \, q$ が有理数、$X$ が無理数で、$p+qX=0$ であるならば、$p=q=0$ であることを証明せよ。
【数Ⅰ】【集合と論証】有理数、無理数の証明 ※問題文は概要欄
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#集合と命題#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の等式を満たすP、Qの値を求めよ
$(1) (\sqrt{ 2 }-1)P+\sqrt{ 2 }Q=2+\sqrt{ 2 }$
$(2)\frac{P}{\sqrt{ 2 }-1}+\frac{Q}{\sqrt{ 2 }}=1$
この動画を見る
次の等式を満たすP、Qの値を求めよ
$(1) (\sqrt{ 2 }-1)P+\sqrt{ 2 }Q=2+\sqrt{ 2 }$
$(2)\frac{P}{\sqrt{ 2 }-1}+\frac{Q}{\sqrt{ 2 }}=1$
【数Ⅰ】【図形と計量】三角比を利用した表し方3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
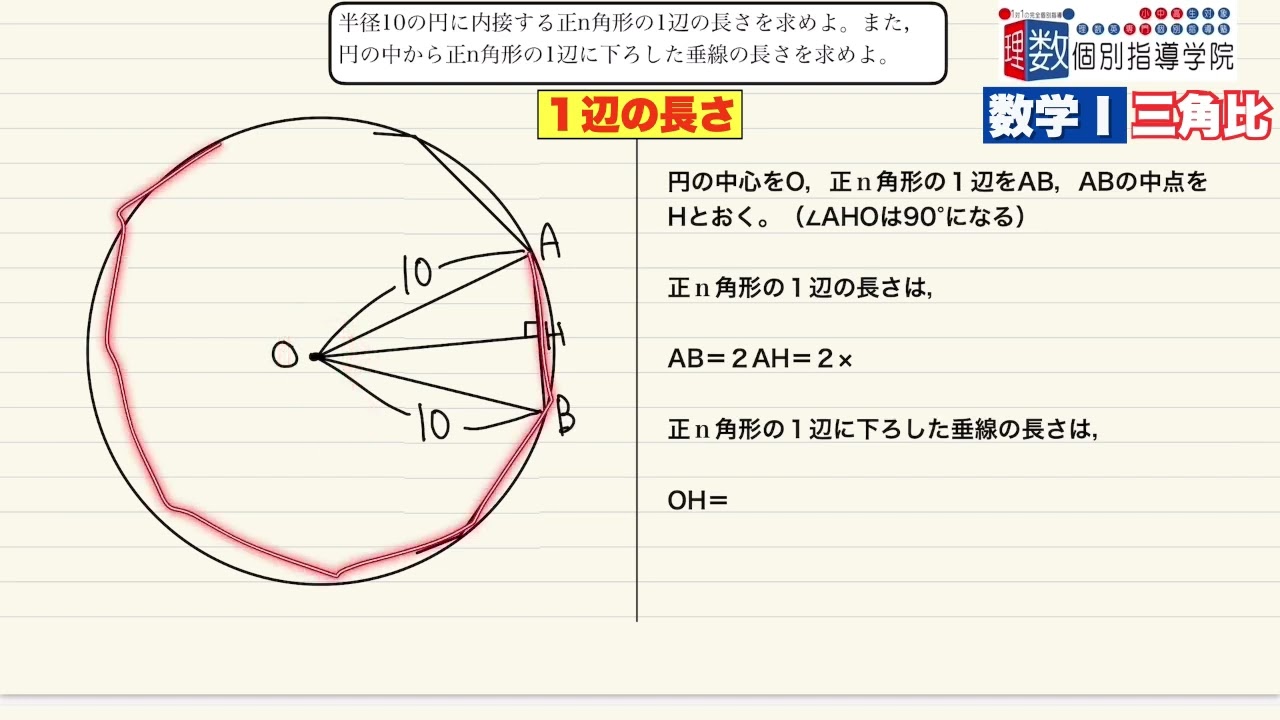
半径10の円に内接する正n角形の1辺の長さを求めよ。また，円の中心から正n角形の1辺に下ろした垂線の長さを求めよ。
この動画を見る
半径10の円に内接する正n角形の1辺の長さを求めよ。また，円の中心から正n角形の1辺に下ろした垂線の長さを求めよ。
【数Ⅰ】【図形と計量】三角比を利用した表し方2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$△ABC$において，$AC=k,\angle A=\alpha, \angle B＝\beta$とする。辺BCの長さを$k,\alpha,\beta$を用いて表せ。ただし,$\alpha,\beta$は鋭角とする。
この動画を見る
$△ABC$において，$AC=k,\angle A=\alpha, \angle B＝\beta$とする。辺BCの長さを$k,\alpha,\beta$を用いて表せ。ただし,$\alpha,\beta$は鋭角とする。
【数Ⅰ】【図形と計量】三角比を利用した表し方1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
∠C=90° である直角三角形ABCにおいて，∠A=θ, AB=k とする。頂点Cから辺ABに下ろした垂線を CD とするとき，次の線分の長さをk，θを用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
この動画を見る
∠C=90° である直角三角形ABCにおいて，∠A=θ, AB=k とする。頂点Cから辺ABに下ろした垂線を CD とするとき，次の線分の長さをk，θを用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
【数Ⅰ】【図形と計量】測量への応用2 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
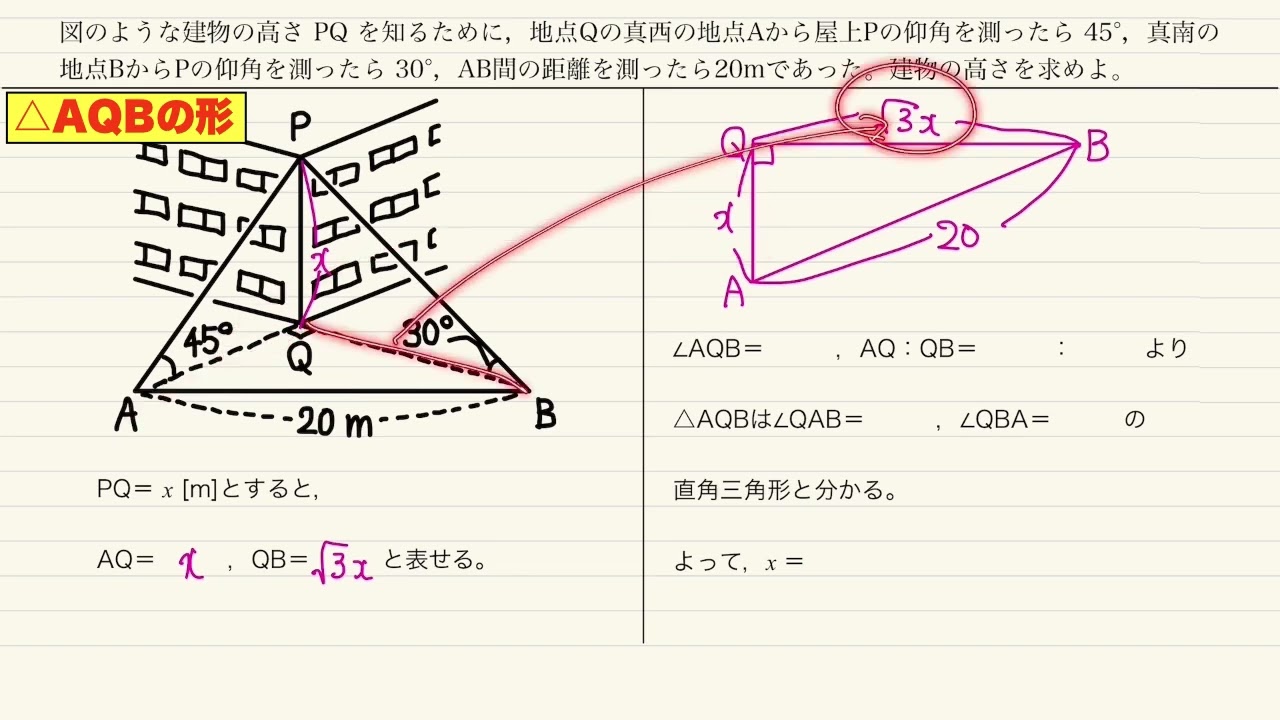
建物の高さ PQ を知るために，地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°，真南の地点BからPの仰角を測ったら 30°，AB間の距離を測ったら20mであった。建物の高さを求めよ。
この動画を見る
建物の高さ PQ を知るために，地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°，真南の地点BからPの仰角を測ったら 30°，AB間の距離を測ったら20mであった。建物の高さを求めよ。
【数Ⅰ】【図形と計量】測量への応用1 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
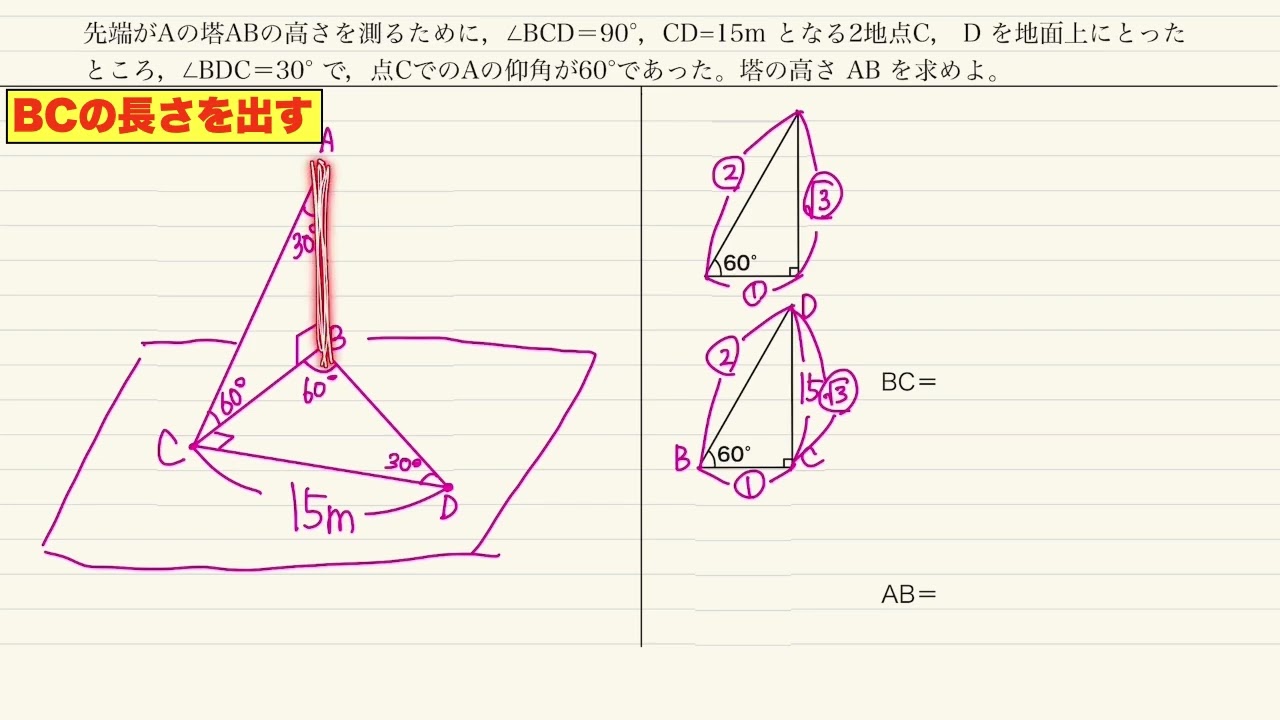
先端がAの塔ABの高さを測るために，∠BCD＝90°，CD=15m となる2地点C， D を地面上にとったところ，∠BDC＝30° で，点CでのAの仰角が60°であった。塔の高さ AB を求めよ。
この動画を見る
先端がAの塔ABの高さを測るために，∠BCD＝90°，CD=15m となる2地点C， D を地面上にとったところ，∠BDC＝30° で，点CでのAの仰角が60°であった。塔の高さ AB を求めよ。
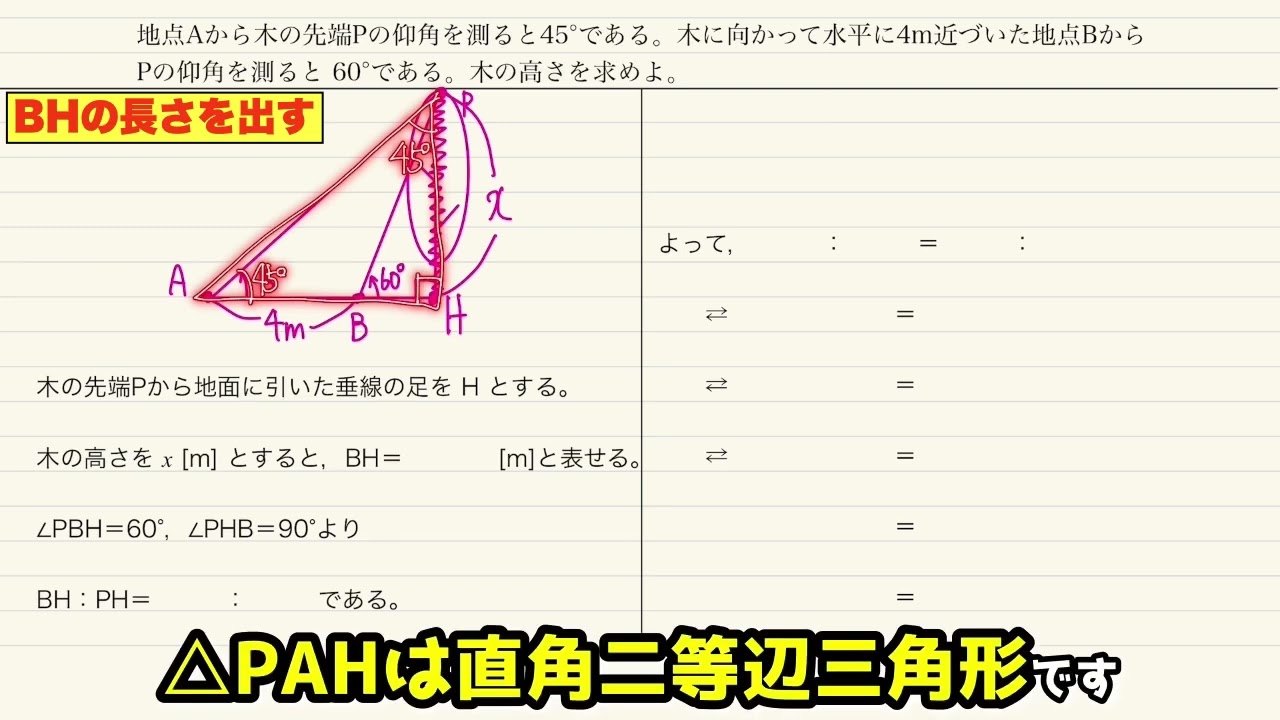
【数Ⅰ】【図形と計量】測量への応用3 ※問題文は概要欄
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
∠C=90° である直角三角形ABCにおいて，∠A=θ, AB=k とする。頂点Cから辺ABに下ろした垂線を CD とするとき，次の線分の長さをk，θを用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
この動画を見る
∠C=90° である直角三角形ABCにおいて，∠A=θ, AB=k とする。頂点Cから辺ABに下ろした垂線を CD とするとき，次の線分の長さをk，θを用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
福田のおもしろ数学313〜1分チャレンジ！数値の計算です
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\frac{2025^4 + 4\times 2024^4}{2024^2+4049^2}-\frac{2023^4+4\times 2024^2}{2024^2+4047^2}$ を計算してください。
この動画を見る
$\frac{2025^4 + 4\times 2024^4}{2024^2+4049^2}-\frac{2023^4+4\times 2024^2}{2024^2+4047^2}$ を計算してください。
【数Ⅰ】【2次関数】関数の場合分け ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
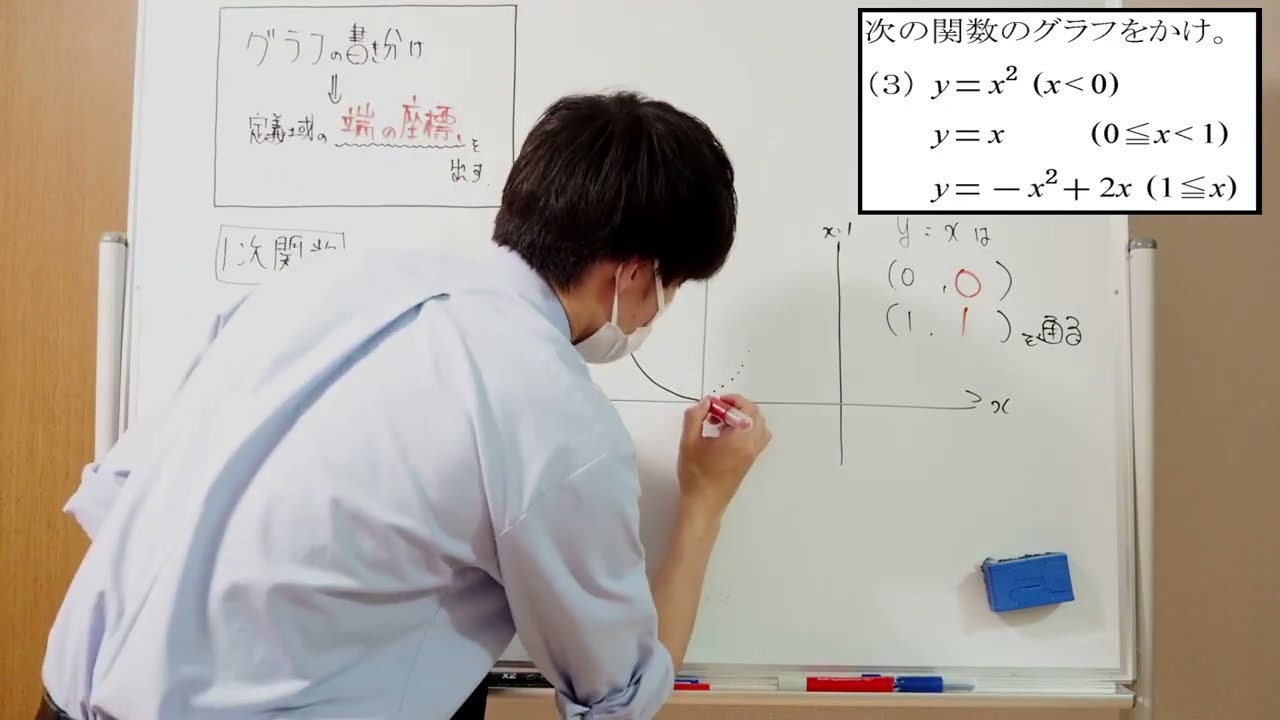
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
この動画を見る
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
福田の数学〜早稲田大学2024社会科学部第3問〜集合と数列
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
この動画を見る
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
【数Ⅰ】【数と式】平方根の式の値 ※問題文は概要欄
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x=\dfrac{\sqrt{ 5 }+2}{\sqrt{ 5 }-2}$ , $y=\dfrac{\sqrt{ 5 }-2}{\sqrt{ 5 }+2}$
のとき, 次の式の値を求めよ。
(1) $x+y$ (2) $xy$ (3) $x^2y+xy^2 $
(4) $x^2+y^2$ (5) $x^3+y^3$
$x=\sqrt{ 2 }-1$
のとき, 次の式の値を求めよ。
(1) $x+\dfrac{1}{x}$ (2) $x^2+\dfrac{1}{x^2}$ (3) $x^3+\dfrac{1}{x^3}$
(4) $x^4+\dfrac{1}{x^4}$ (5) $x^5+\dfrac{1}{x^5}$
この動画を見る
$x=\dfrac{\sqrt{ 5 }+2}{\sqrt{ 5 }-2}$ , $y=\dfrac{\sqrt{ 5 }-2}{\sqrt{ 5 }+2}$
のとき, 次の式の値を求めよ。
(1) $x+y$ (2) $xy$ (3) $x^2y+xy^2 $
(4) $x^2+y^2$ (5) $x^3+y^3$
$x=\sqrt{ 2 }-1$
のとき, 次の式の値を求めよ。
(1) $x+\dfrac{1}{x}$ (2) $x^2+\dfrac{1}{x^2}$ (3) $x^3+\dfrac{1}{x^3}$
(4) $x^4+\dfrac{1}{x^4}$ (5) $x^5+\dfrac{1}{x^5}$
【数A】【場合の数】集合の個数 ※問題文は概要欄
単元：
#数Ⅰ#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
全体集合Uと、その部分集合$A$,$B$に対して${}_{ n }$U = 50,${}_{ n }$($A$$\cup$$B$) = 42,${}_{ n }$($A$$\cap$$B$) = 3, ${}_{ n }$($\overline{A}$$\cap$$B$) = 15であるとき、次の集合の要素の個数を求めよ。
(1) $\overline{A}$$\cap$$\overline{B}$ (2) $A$$\cap$$\overline{B}$ (3) $A$
この動画を見る
全体集合Uと、その部分集合$A$,$B$に対して${}_{ n }$U = 50,${}_{ n }$($A$$\cup$$B$) = 42,${}_{ n }$($A$$\cap$$B$) = 3, ${}_{ n }$($\overline{A}$$\cap$$B$) = 15であるとき、次の集合の要素の個数を求めよ。
(1) $\overline{A}$$\cap$$\overline{B}$ (2) $A$$\cap$$\overline{B}$ (3) $A$
【数Ⅰ】【数と式】平方根の式の値 ※問題文は概要欄
単元：
#数Ⅰ#数と式#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x$=$\cfrac{\sqrt{5}+2}{\sqrt{5}-2}$ , $y$ = $\cfrac{\sqrt{5}-2}{\sqrt{5}+2}$ のとき、次の式の値を求めよ
(1) $x$+$y$ (2)$xy$ (3) $x^2y+xy^2$ (4)$x^2+y^2$ (5)$x^3+y^3$
この動画を見る
$x$=$\cfrac{\sqrt{5}+2}{\sqrt{5}-2}$ , $y$ = $\cfrac{\sqrt{5}-2}{\sqrt{5}+2}$ のとき、次の式の値を求めよ
(1) $x$+$y$ (2)$xy$ (3) $x^2y+xy^2$ (4)$x^2+y^2$ (5)$x^3+y^3$
【数A】【場合の数】集合の文章題 ※問題文は概要欄
単元：
#数A#場合の数と確率#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
海外旅行者100人のうち、75人がカゼ薬を、80人が胃薬を携帯していた。次のような人は、最も多くて何人か。また少なくて何人か。
(1)カゼ薬と胃薬を両方とも携帯した人
(2)カゼ薬と胃薬を両方とも携帯していない人
この動画を見る
海外旅行者100人のうち、75人がカゼ薬を、80人が胃薬を携帯していた。次のような人は、最も多くて何人か。また少なくて何人か。
(1)カゼ薬と胃薬を両方とも携帯した人
(2)カゼ薬と胃薬を両方とも携帯していない人
【数A】【場合の数】3つの集合 ※問題文は概要欄
単元：
#数A#場合の数と確率#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
1から100までの整数のうち、次のような数は何個あるか。
(1)2,3,7の少なくとも1つで割り切れる数
(2)2では割り切れるが、3でも7でも割り切れない数
この動画を見る
1から100までの整数のうち、次のような数は何個あるか。
(1)2,3,7の少なくとも1つで割り切れる数
(2)2では割り切れるが、3でも7でも割り切れない数
【数Ⅰ】【数と式】平方根の近似値 ※問題文は概要欄
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\sqrt{2}=1.4142$, $\sqrt{3}=1.7321$
とするとき, 分母の有理化を利用して, 次の値を求めよ。
(1) $\dfrac{10}{\sqrt{3}+\sqrt{2}}$ (2) $\dfrac{1}{\sqrt{12}-\sqrt{2}}$
$x=1-\sqrt{5}$
のとき, 次の式の値を求めよ。
(1) $x^2－2x－4$ (2) $x^3－2x^2$
この動画を見る
$\sqrt{2}=1.4142$, $\sqrt{3}=1.7321$
とするとき, 分母の有理化を利用して, 次の値を求めよ。
(1) $\dfrac{10}{\sqrt{3}+\sqrt{2}}$ (2) $\dfrac{1}{\sqrt{12}-\sqrt{2}}$
$x=1-\sqrt{5}$
のとき, 次の式の値を求めよ。
(1) $x^2－2x－4$ (2) $x^3－2x^2$
【数 I】【数と式】平方根の近似値
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\sqrt{2}=1.4142,\ \sqrt{3}=1.7321\ とするとき, \ 分母の有理化を利用して,\ 次の値を求めよ。\\\\$
$(1) \ \frac{10}{\sqrt{3}+\sqrt{2}}\ (2)\ \frac{1}{\sqrt{12}-\sqrt{2}}$
この動画を見る
$\sqrt{2}=1.4142,\ \sqrt{3}=1.7321\ とするとき, \ 分母の有理化を利用して,\ 次の値を求めよ。\\\\$
$(1) \ \frac{10}{\sqrt{3}+\sqrt{2}}\ (2)\ \frac{1}{\sqrt{12}-\sqrt{2}}$
【数Ⅰ】【数と式】平方根の計算 ※問題文は概要欄
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の計算をせよ。
(1) $(1+\sqrt{ 2 }-\sqrt{ 3 })^2$
(2)$(3-\sqrt{ 2 }-\sqrt{ 11 })(3-\sqrt{ 2 }+\sqrt{ 11 })$
次の計算をせよ。
(1) $\displaystyle \frac{3\sqrt{ 5 }-5\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}+\displaystyle \frac{3\sqrt{ 5 }+4\sqrt{ 3 }}{3\sqrt{ 5 }-4\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 2 }-1}{\sqrt{ 2 }+1}+\displaystyle \frac{\sqrt{ 3 }-\sqrt{ 2 }}{\sqrt{ 3 }+\sqrt{ 2 }}+\displaystyle \frac{\sqrt{ 3 }+\sqrt{ 2 }}{2-\sqrt{ 3 }}$
次の計算をせよ。
(1) $\displaystyle \frac{1}{1+\sqrt{ 2 }-\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }+\sqrt{ 2 }}{\sqrt{ 5 }+\sqrt{ 3 }-\sqrt{ 2 }}$
(3) $\displaystyle \frac{\sqrt{ 2 }+\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }+\sqrt{ 5 }-\sqrt{ 7 }}+\displaystyle \frac{\sqrt{ 2 }-\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }-\sqrt{ 5 }-\sqrt{ 7 }}$
この動画を見る
次の計算をせよ。
(1) $(1+\sqrt{ 2 }-\sqrt{ 3 })^2$
(2)$(3-\sqrt{ 2 }-\sqrt{ 11 })(3-\sqrt{ 2 }+\sqrt{ 11 })$
次の計算をせよ。
(1) $\displaystyle \frac{3\sqrt{ 5 }-5\sqrt{ 3 }}{\sqrt{ 5 }+\sqrt{ 3 }}+\displaystyle \frac{3\sqrt{ 5 }+4\sqrt{ 3 }}{3\sqrt{ 5 }-4\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 2 }-1}{\sqrt{ 2 }+1}+\displaystyle \frac{\sqrt{ 3 }-\sqrt{ 2 }}{\sqrt{ 3 }+\sqrt{ 2 }}+\displaystyle \frac{\sqrt{ 3 }+\sqrt{ 2 }}{2-\sqrt{ 3 }}$
次の計算をせよ。
(1) $\displaystyle \frac{1}{1+\sqrt{ 2 }-\sqrt{ 3 }}$
(2) $\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }+\sqrt{ 2 }}{\sqrt{ 5 }+\sqrt{ 3 }-\sqrt{ 2 }}$
(3) $\displaystyle \frac{\sqrt{ 2 }+\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }+\sqrt{ 5 }-\sqrt{ 7 }}+\displaystyle \frac{\sqrt{ 2 }-\sqrt{ 5 }+\sqrt{ 7 }}{\sqrt{ 2 }-\sqrt{ 5 }-\sqrt{ 7 }}$
【数Ⅰ】【数と式】循環小数と絶対値 ※問題文は概要欄
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の分数を小数で表したとき、[ ]内の数字を求めよ。
(1) $\frac{11}{101}$ (2) $\frac{9}{41}$
x=-4,-1,2,5 のそれぞれについて、次の式の値を求めよ。
(1)｜-x｜ (2)｜x+1｜ (3)｜1-2x｜+｜x-1｜
この動画を見る
次の分数を小数で表したとき、[ ]内の数字を求めよ。
(1) $\frac{11}{101}$ (2) $\frac{9}{41}$
x=-4,-1,2,5 のそれぞれについて、次の式の値を求めよ。
(1)｜-x｜ (2)｜x+1｜ (3)｜1-2x｜+｜x-1｜