 図形の性質
図形の性質
 図形の性質
図形の性質
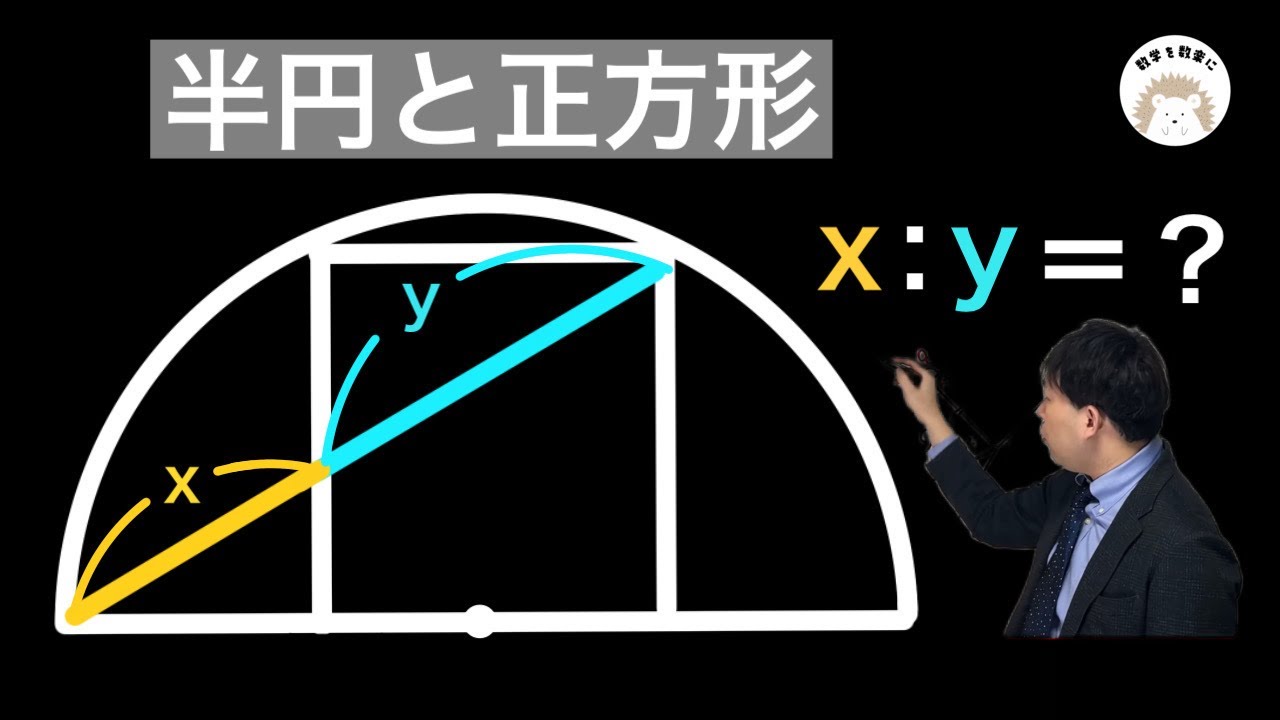
半円と正方形
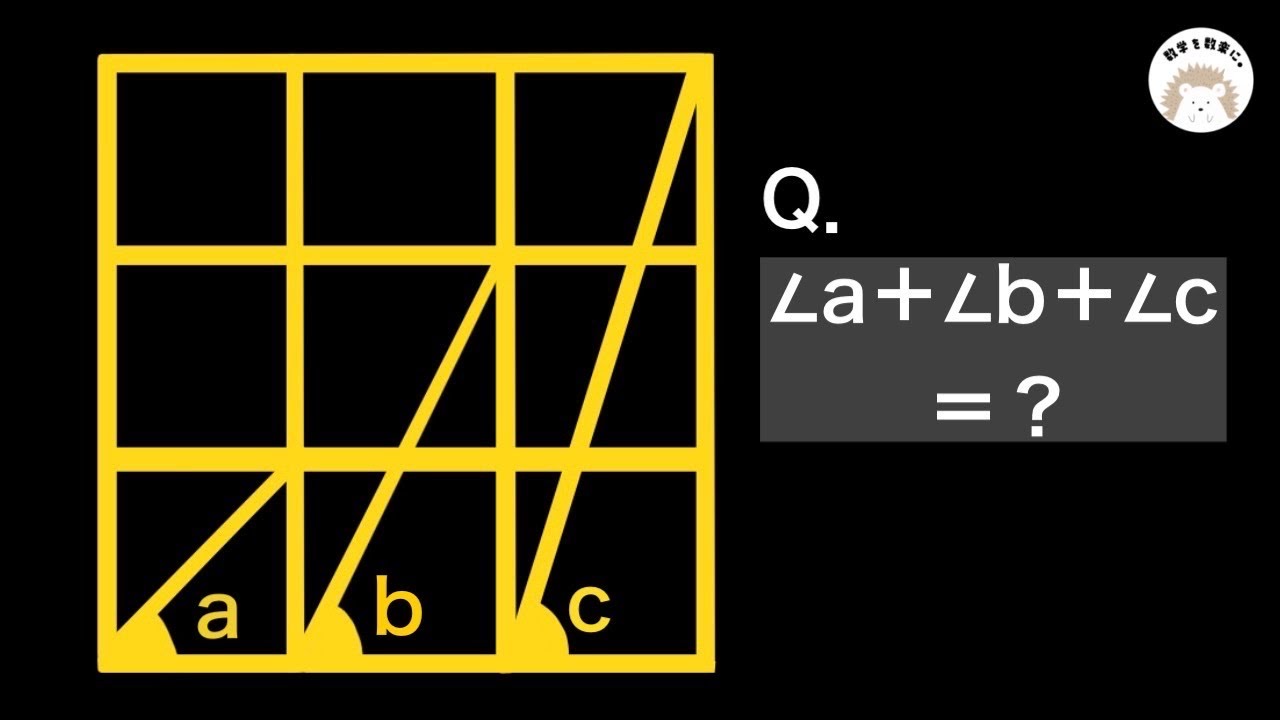
9つの正方形と角の和
単元:
#数学(中学生)#中2数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a + \angle b +\angle c=? $
*図は動画内参照
この動画を見る
$\angle a + \angle b +\angle c=? $
*図は動画内参照
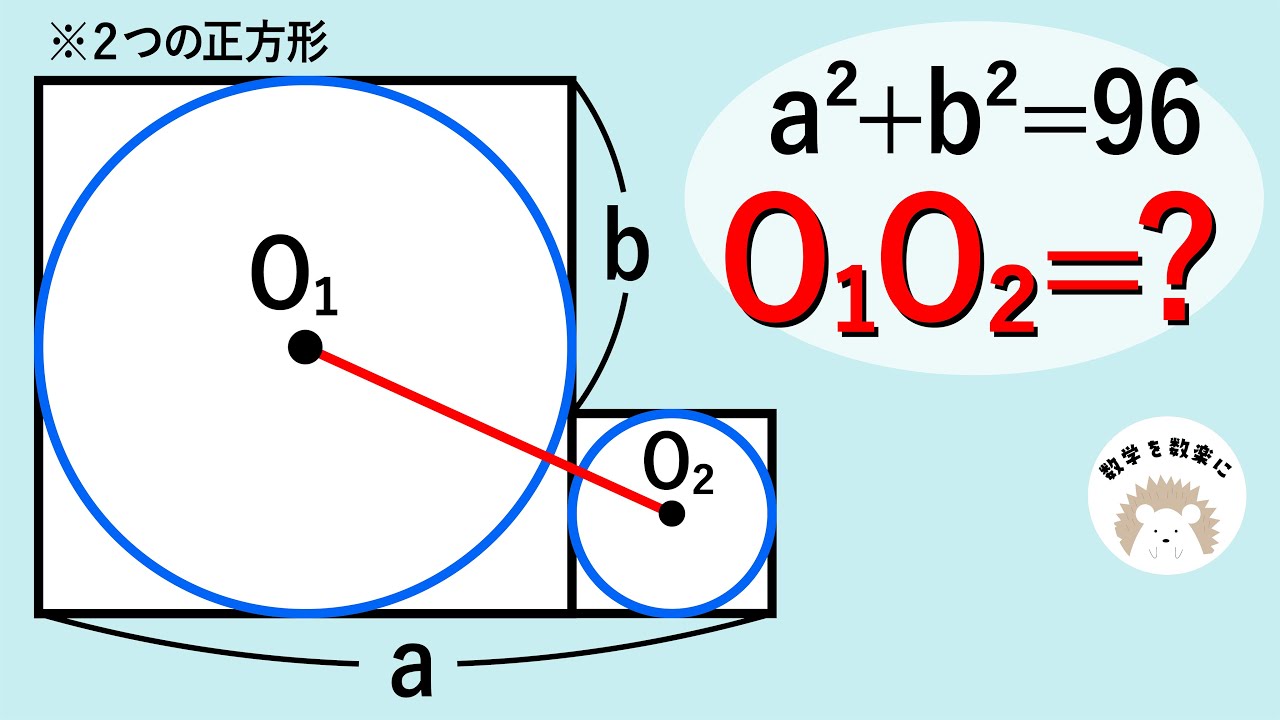
2つの円
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
*2つの正方形
$a^2+b^2=96$
$O_1O_2=?$
*図は動画内参照
この動画を見る
*2つの正方形
$a^2+b^2=96$
$O_1O_2=?$
*図は動画内参照
三角形の面積

福田の入試問題解説〜北海道大学2022年文系第3問〜直角三角形と内接円

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
この動画を見る
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
気づけば!知っていれば一瞬!!

気づけば一瞬!!コラボ ベリースライム
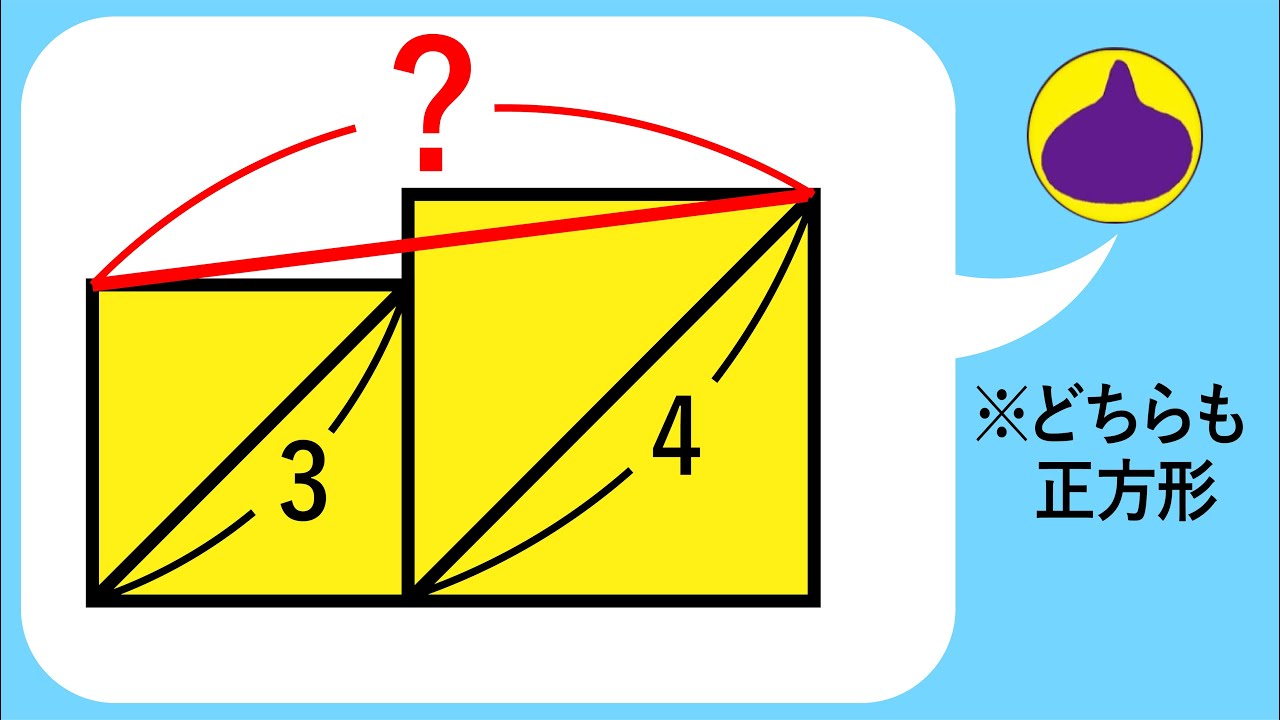
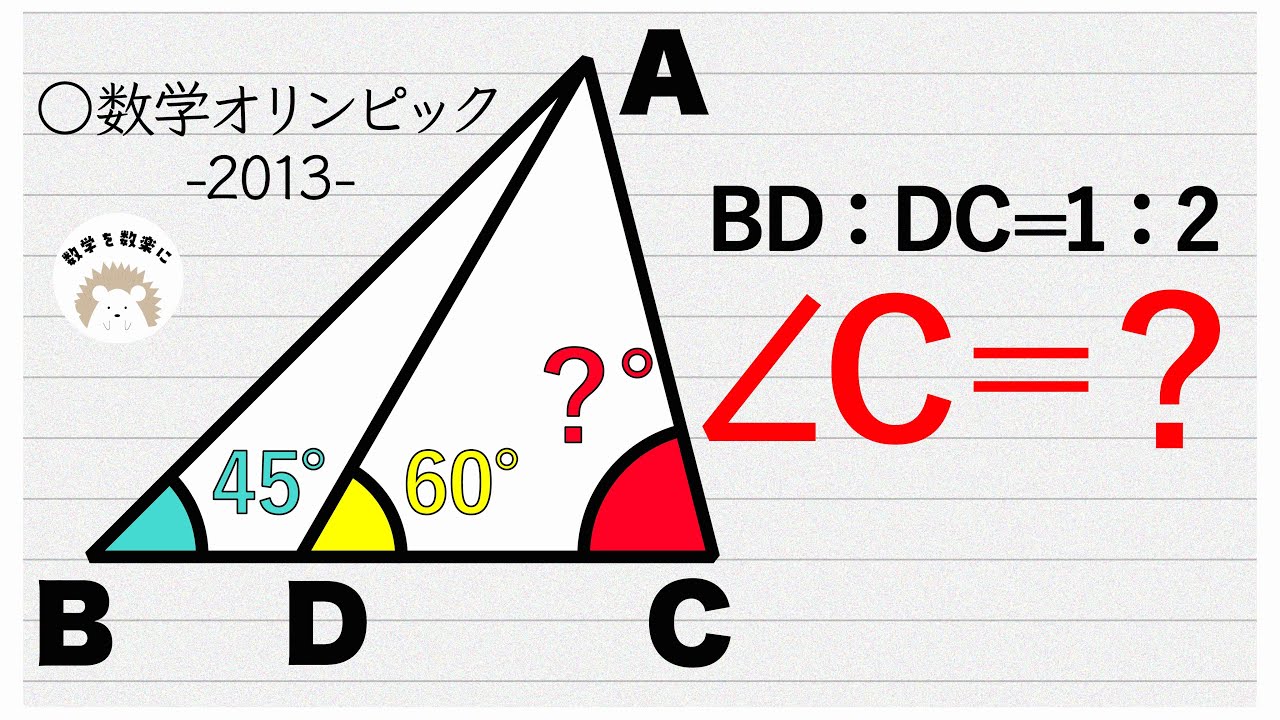
シンガポール数学オリンピックの問題
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学オリンピック#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BD:DC=1:2
$\angle C=?$
*図は動画内参照
2013数学オリンピック
この動画を見る
BD:DC=1:2
$\angle C=?$
*図は動画内参照
2013数学オリンピック
福田の数学・入試問題解説〜東北大学2022年理系第4問〜2つの直線に接し互いに外接する2つの円の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
この動画を見る
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
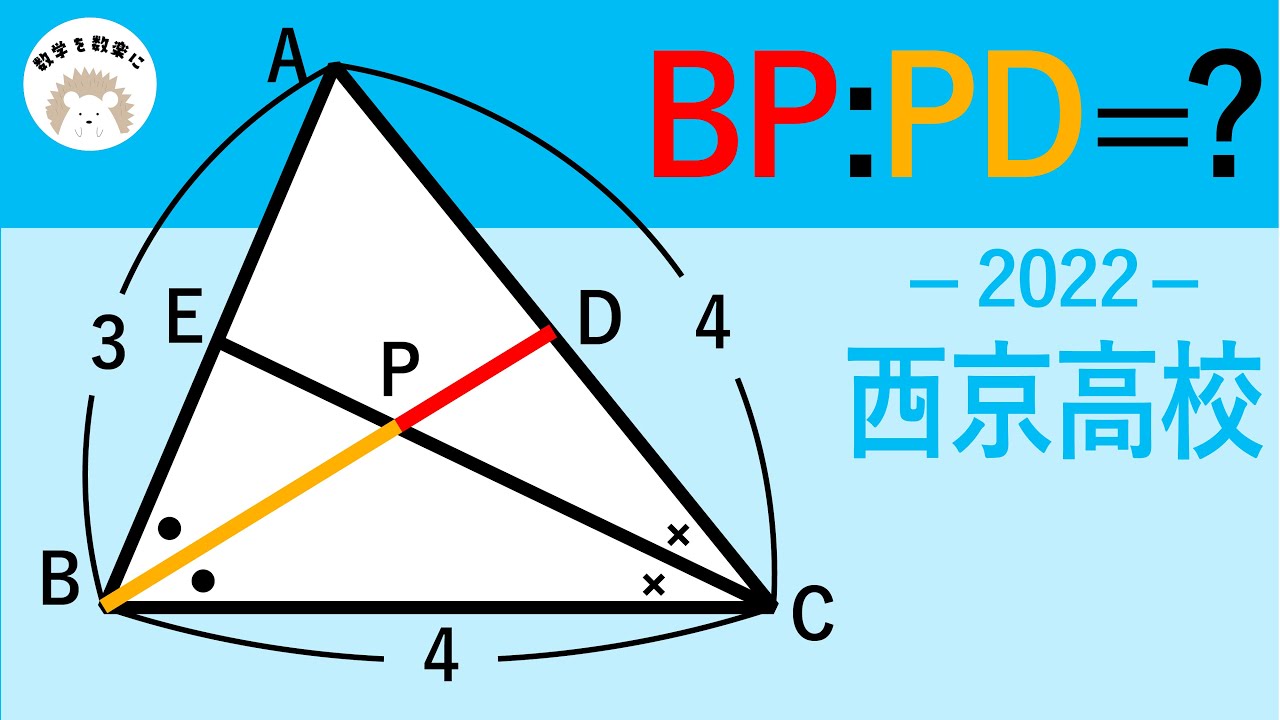
内閣の二等分線 西京高校 2022 入試から観る数学の世界
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BP:PD=?
*図は動画内参照
2022西京高等学校
この動画を見る
BP:PD=?
*図は動画内参照
2022西京高等学校
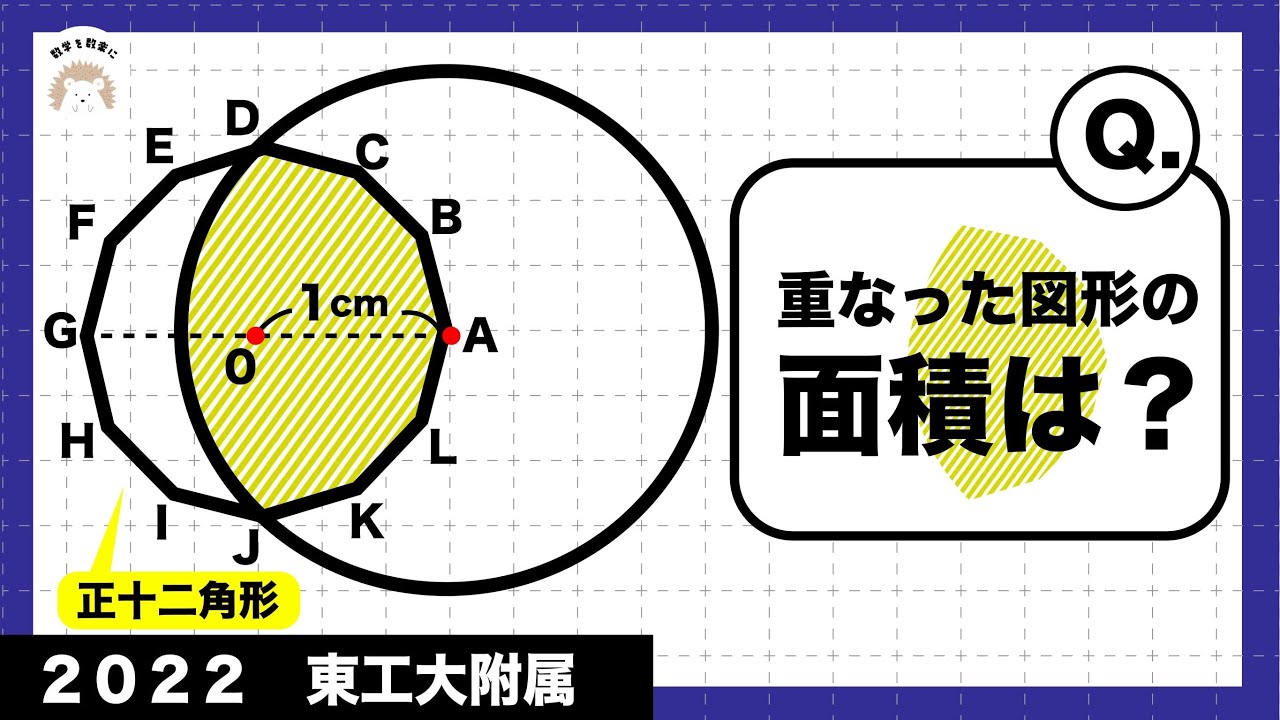
正十二角形と円 東工大附属
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
重なった図形の面積は?
*図は動画内参照
2022東京工業大学附属科学技術高等学校
この動画を見る
重なった図形の面積は?
*図は動画内参照
2022東京工業大学附属科学技術高等学校
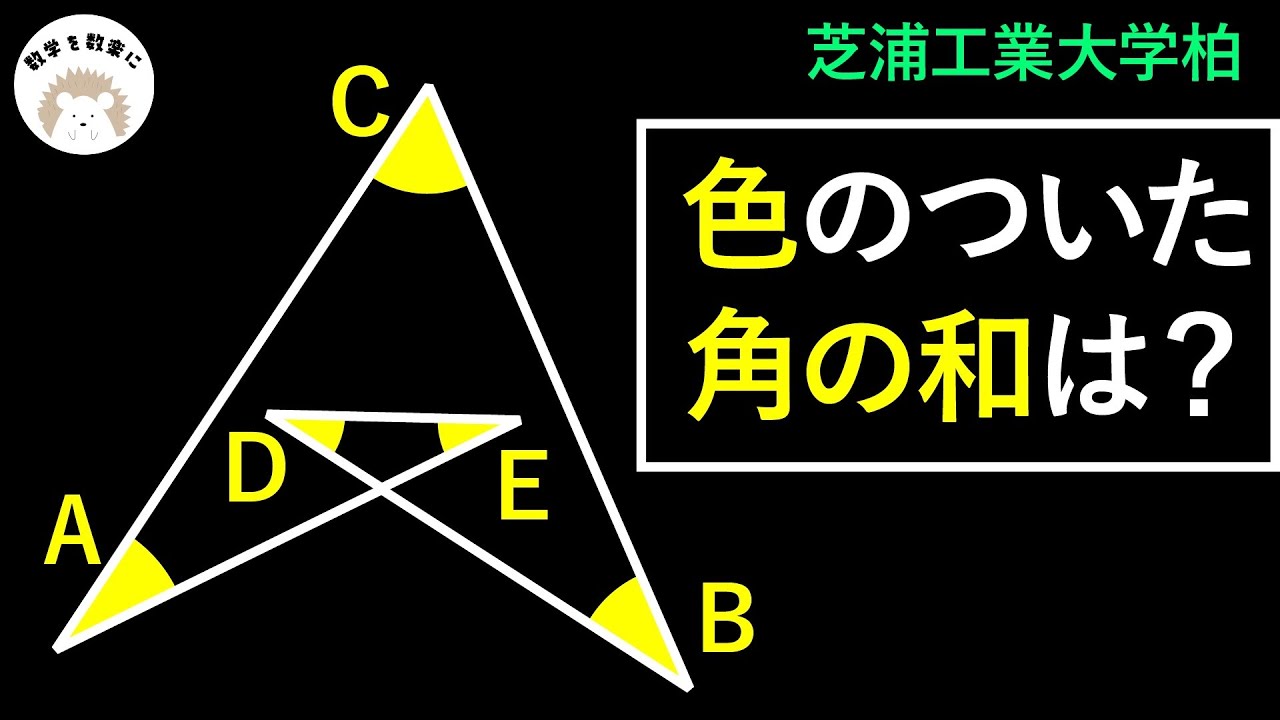
角の和 2通りで解説!!芝浦工大柏
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a +\angle b +\angle c + \angle d + \angle e =?$
*図は動画内参照
芝浦工業大学柏中学高等学校
この動画を見る
$\angle a +\angle b +\angle c + \angle d + \angle e =?$
*図は動画内参照
芝浦工業大学柏中学高等学校
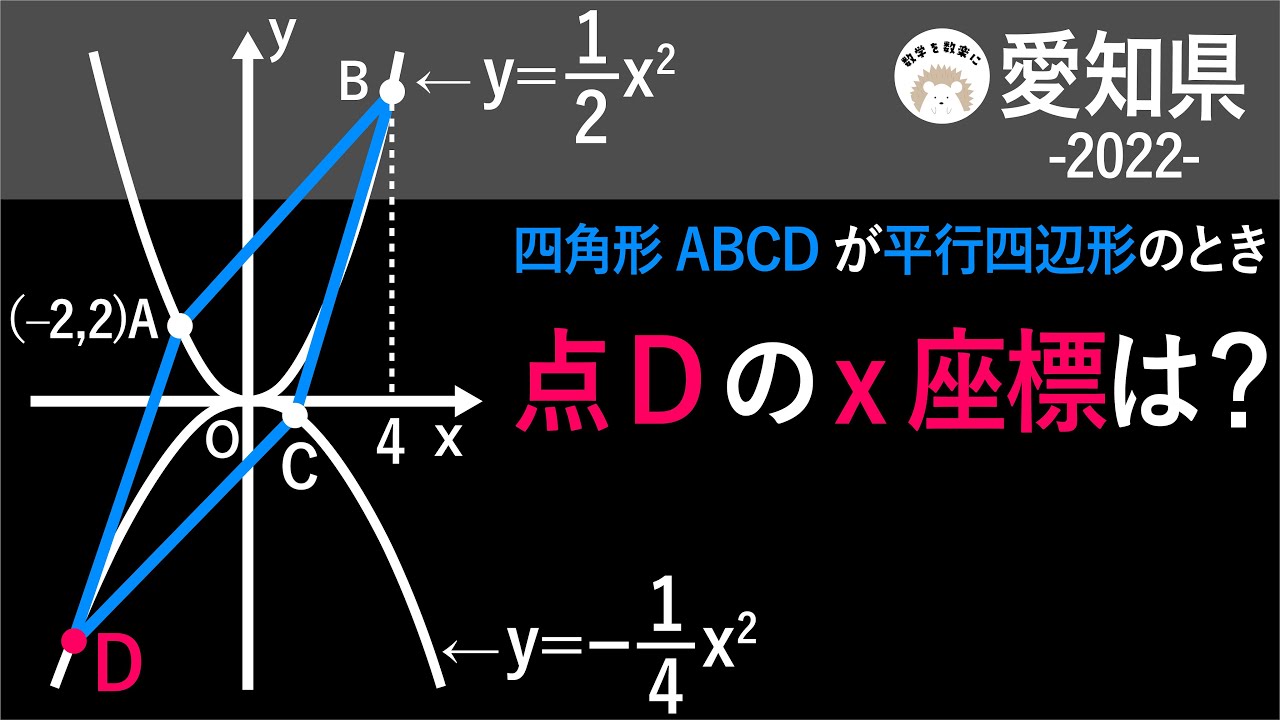
座標平面上の平行四辺形 令和4年度 2022 入試問題100題解説97問目! 愛知県
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#平面上の曲線#図形と計量#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABCDが平行四辺形のとき点Dのx座標は?
*図は動画内参照
2022愛知県
この動画を見る
四角形ABCDが平行四辺形のとき点Dのx座標は?
*図は動画内参照
2022愛知県
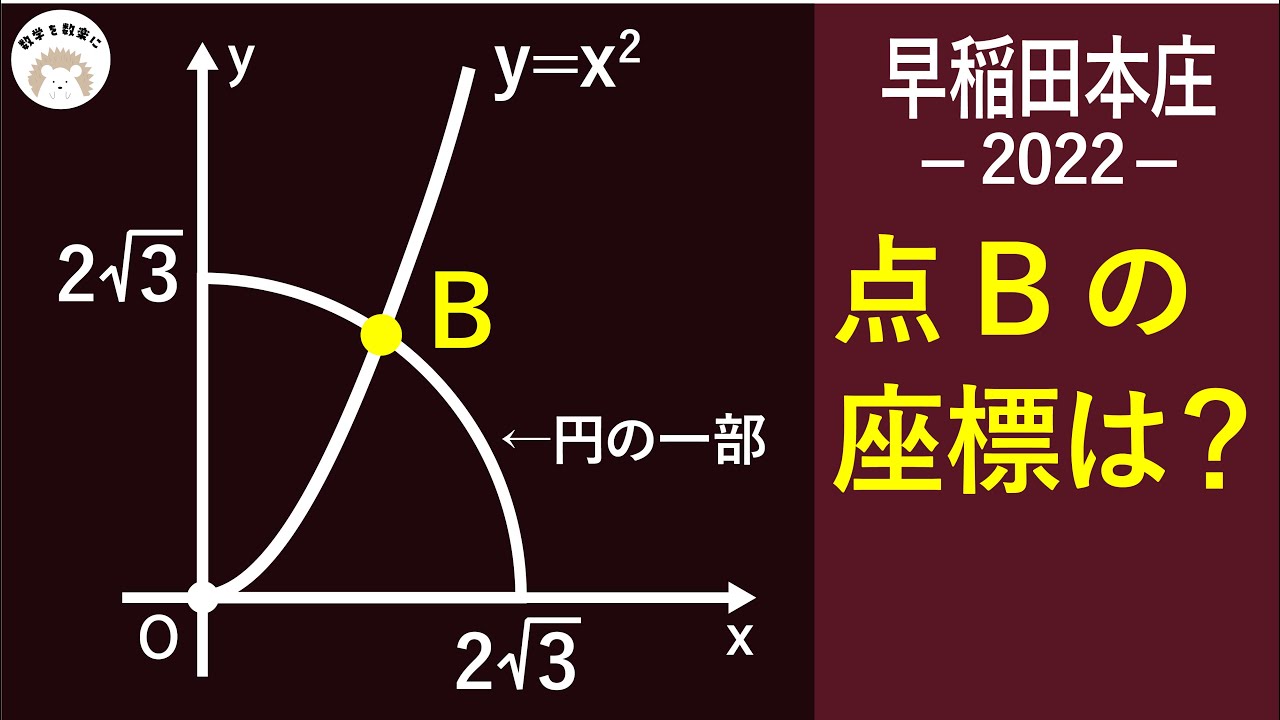
放物線と円 早稲田本庄 令和4年度 2022 入試問題100題解説96問目!
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Bの座標は?
*図は動画内参照
2022早稲田大学 本庄高等学院
この動画を見る
点Bの座標は?
*図は動画内参照
2022早稲田大学 本庄高等学院
チェバの定理を使いますか?
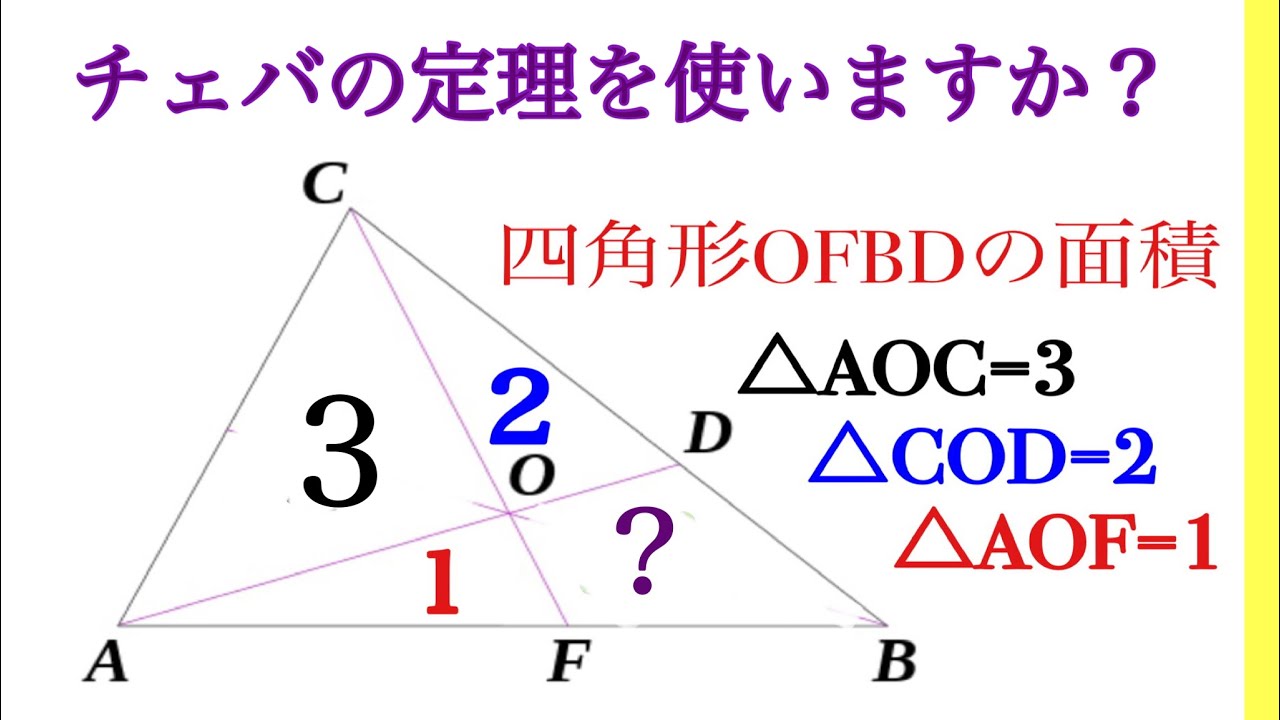
チェバの定理を使いますか?

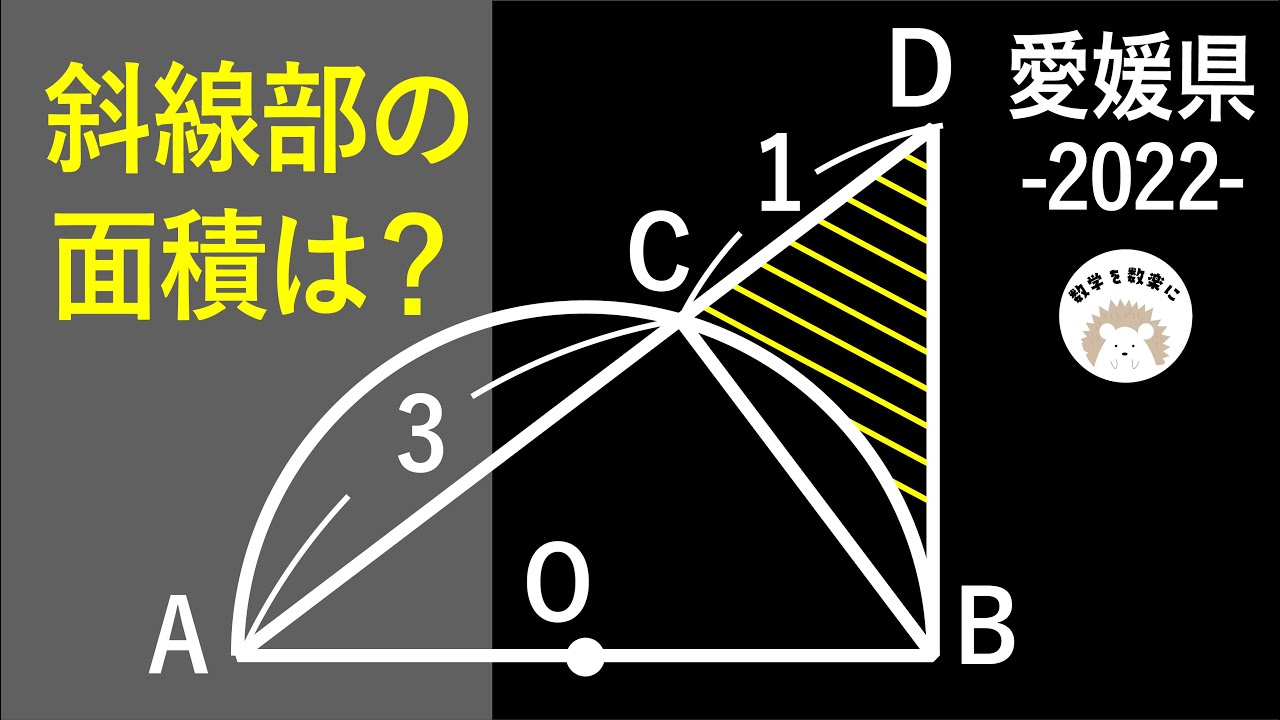
おうぎ形と正方形 令和4年度 愛媛県ラスト問題(改) 数学 2022 入試問題100題解説83問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積は?
*図は動画内参照
2022愛媛県
この動画を見る
斜線部の面積は?
*図は動画内参照
2022愛媛県
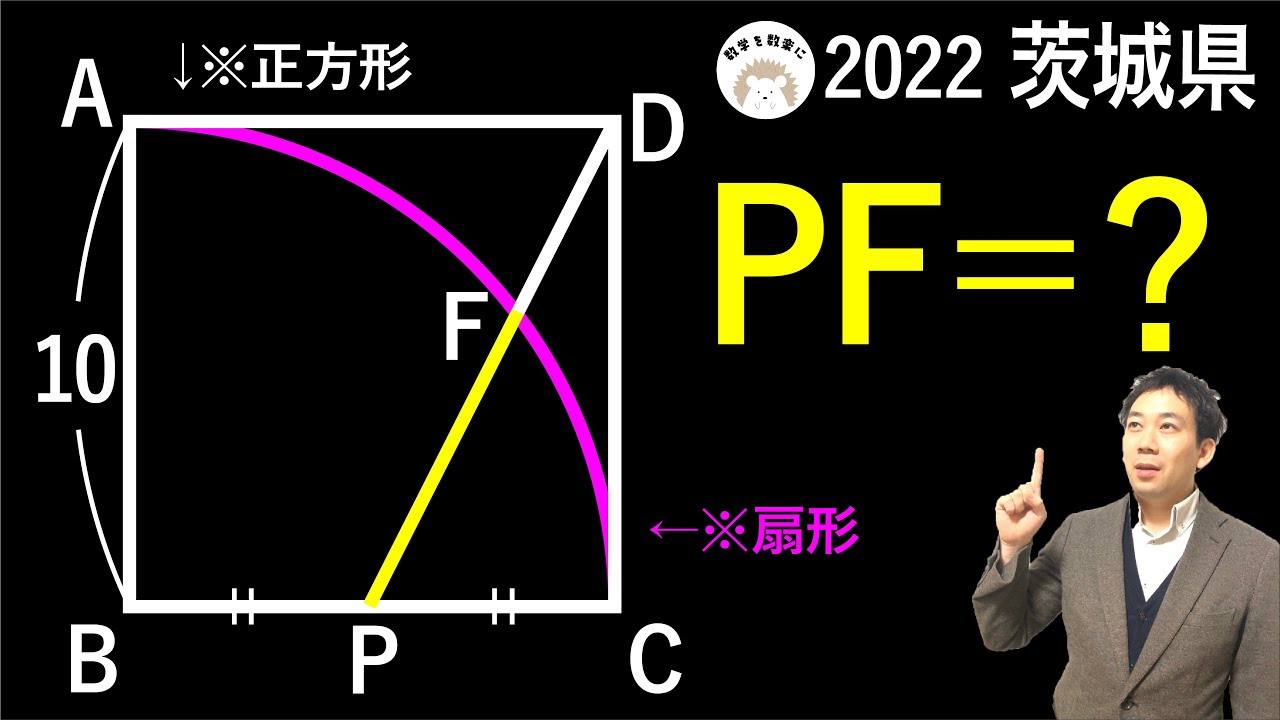
おうぎ形と正方形 2通りで解説!令和4年度 茨城県 数学 2022 入試問題100題解説81問目!
単元:
#数学(中学生)#中2数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点PはBCの中点
PF=?
*図は動画内参照
2022茨城県
この動画を見る
点PはBCの中点
PF=?
*図は動画内参照
2022茨城県
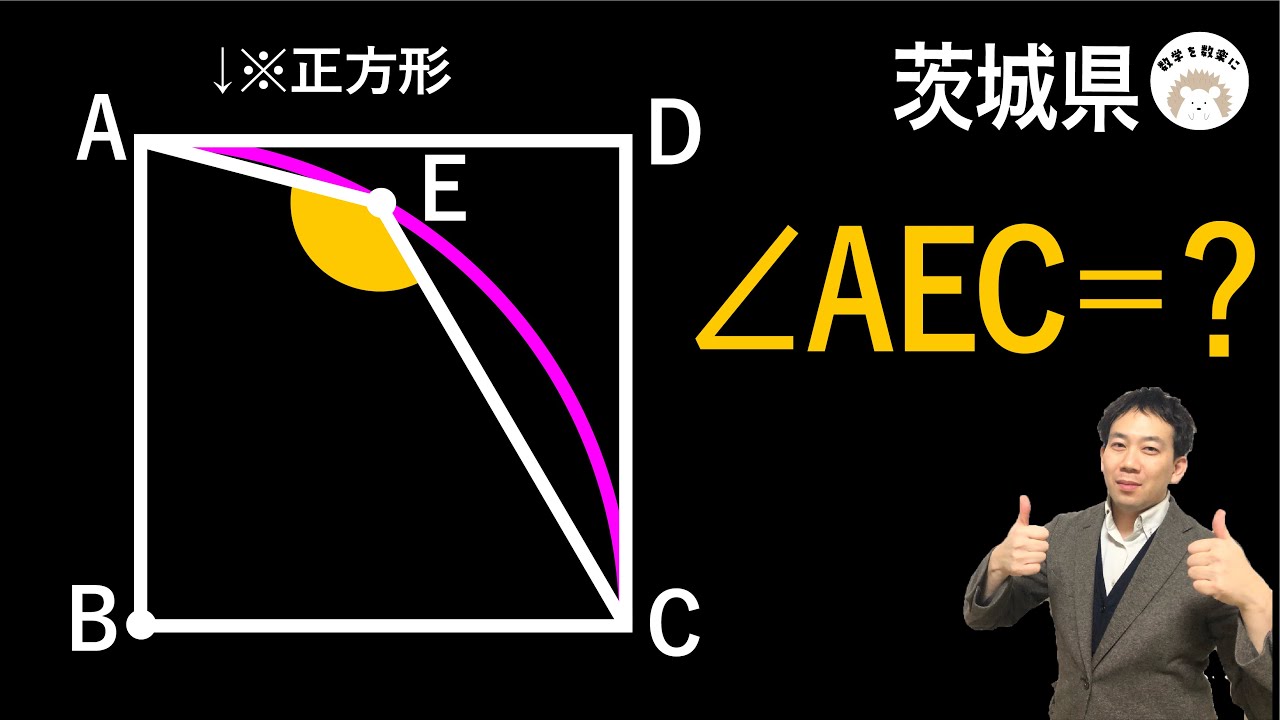
おうぎ形と正方形 令和4年度 茨城県 数学 2022 入試問題100題解説80問目!
福田の数学〜慶應義塾大学2022年薬学部第1問(7)〜直三角柱の切断面の面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形の性質#微分法と積分法#学校別大学入試過去問解説(数学)#立体図形#立体切断#空間における垂直と平行と多面体(オイラーの法則)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
この動画を見る
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
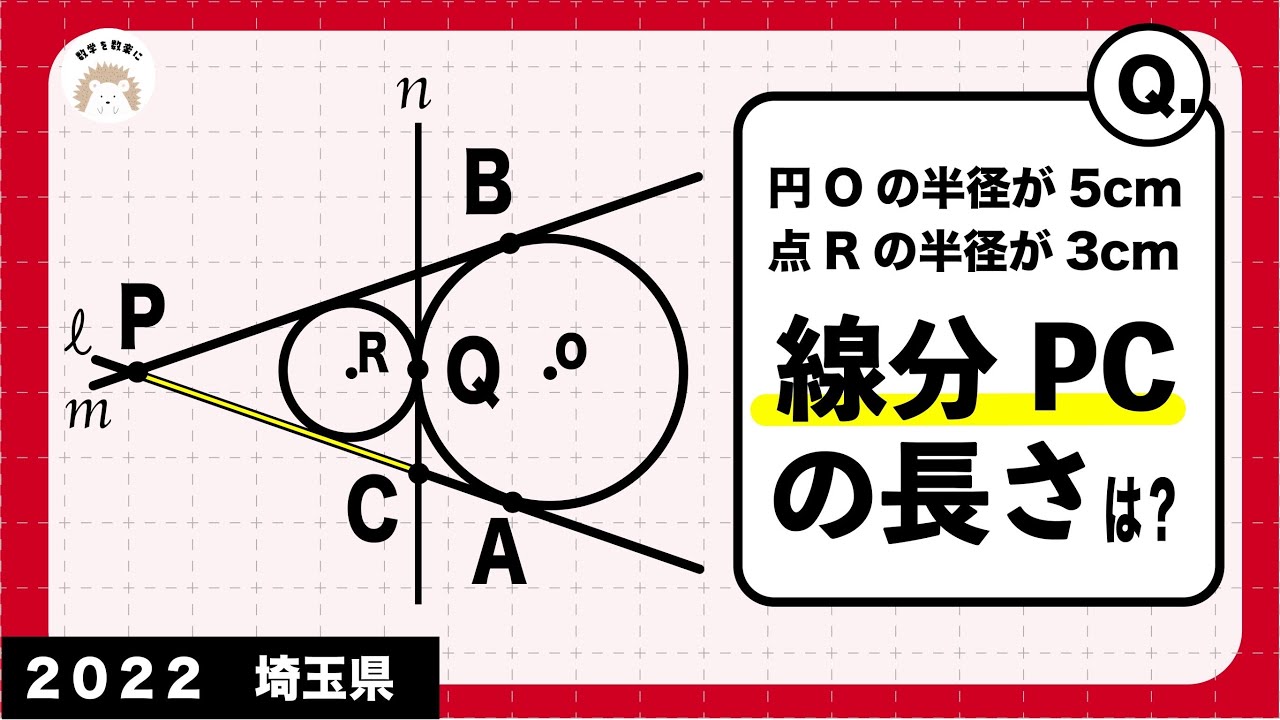
2つの円 埼玉県 令和4年度 数学 2022 入試問題100題解説77問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
この動画を見る
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
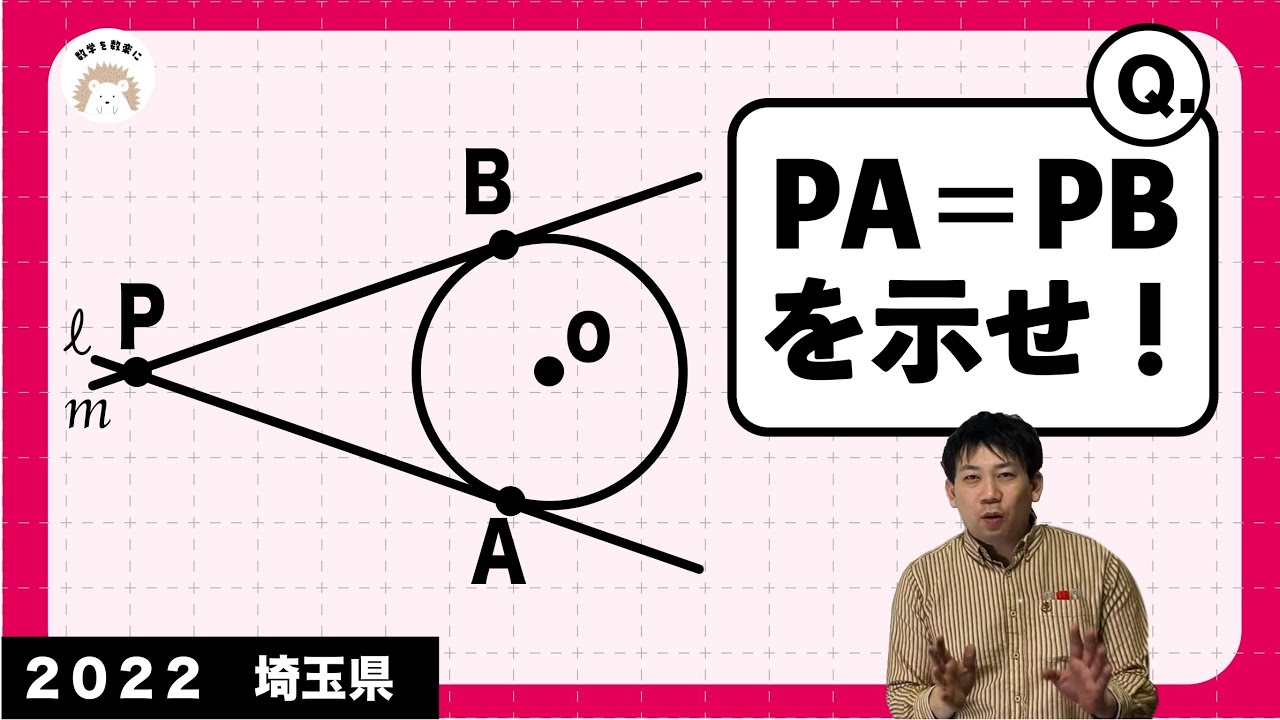
接線の長さが等しいことの証明 埼玉県 令和4年度 数学 2022 入試問題100題解説76問目!
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
PA=PBを示せ
*図は動画内参照
2022埼玉県
この動画を見る
PA=PBを示せ
*図は動画内参照
2022埼玉県
【数A】図形の性質:<これを見て思い出そう>三角形の重心の性質 ~何対何?~

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
この動画を見る
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
福田の数学〜東京慈恵会医科大学2022年医学部第4問〜複素数平面と図形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上の曲線#複素数平面#方べきの定理と2つの円の関係#図形と方程式#点と直線#2次曲線#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
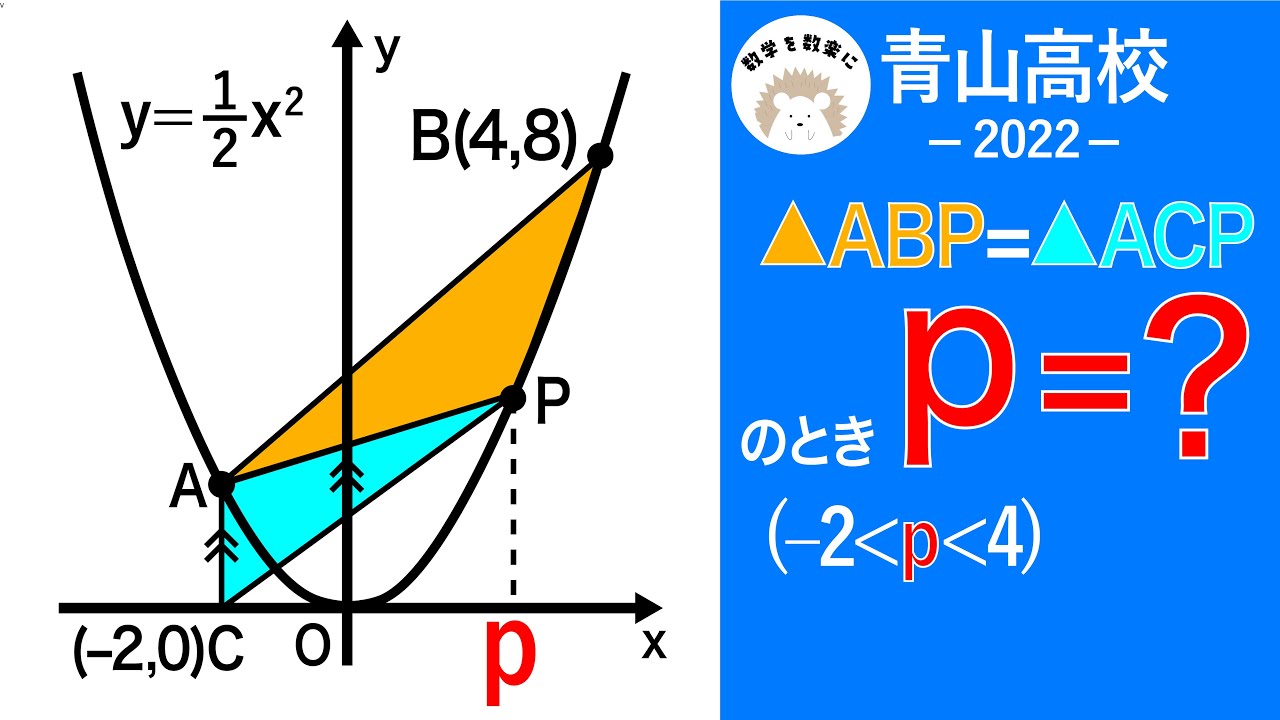
面積について方程式を立てず解くこともできます。青山高校 関数 2022 入試問題100題解説72問目!!
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABP=△ACPのとき
p=?(-2<p<4)
*図は動画内参照
2022青山高等学校
この動画を見る
△ABP=△ACPのとき
p=?(-2<p<4)
*図は動画内参照
2022青山高等学校
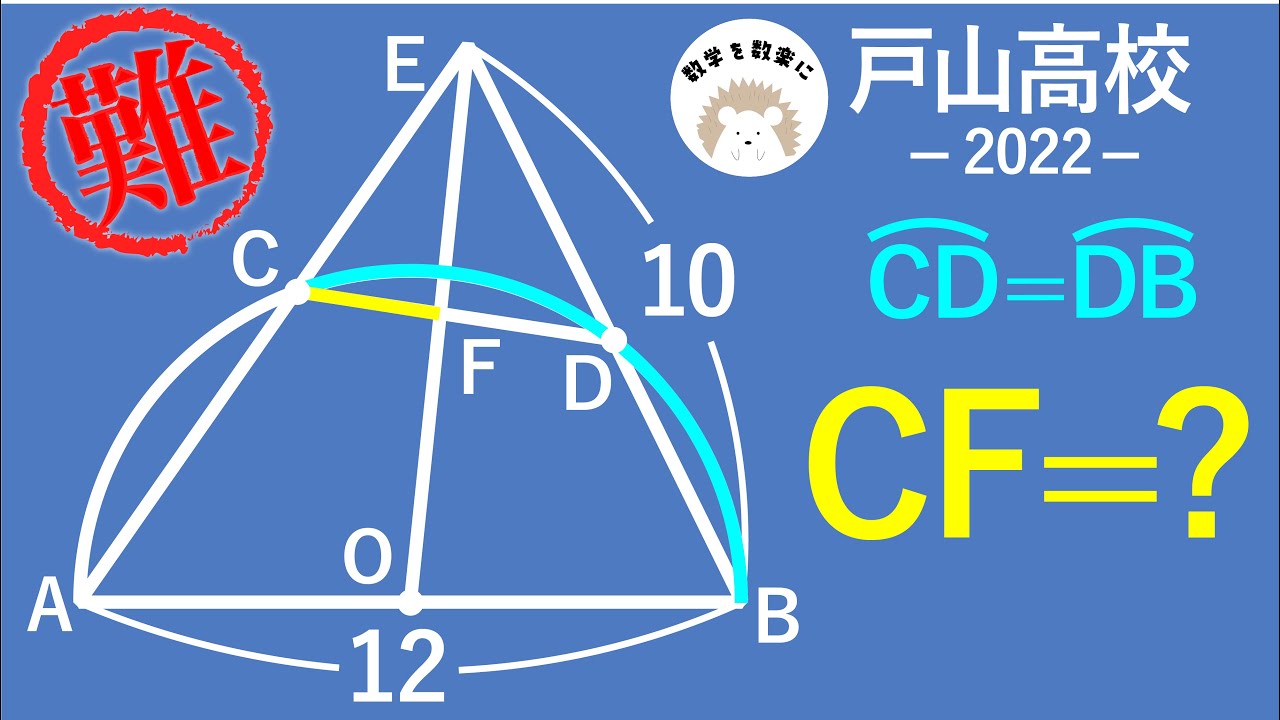
戸山高校 2022 入試問題100題解説71問目!!
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{CD}$ = $\stackrel{\huge\frown}{DB}$
CF=?
*図は動画内参照
2022戸山高等学校
この動画を見る
$\stackrel{\huge\frown}{CD}$ = $\stackrel{\huge\frown}{DB}$
CF=?
*図は動画内参照
2022戸山高等学校
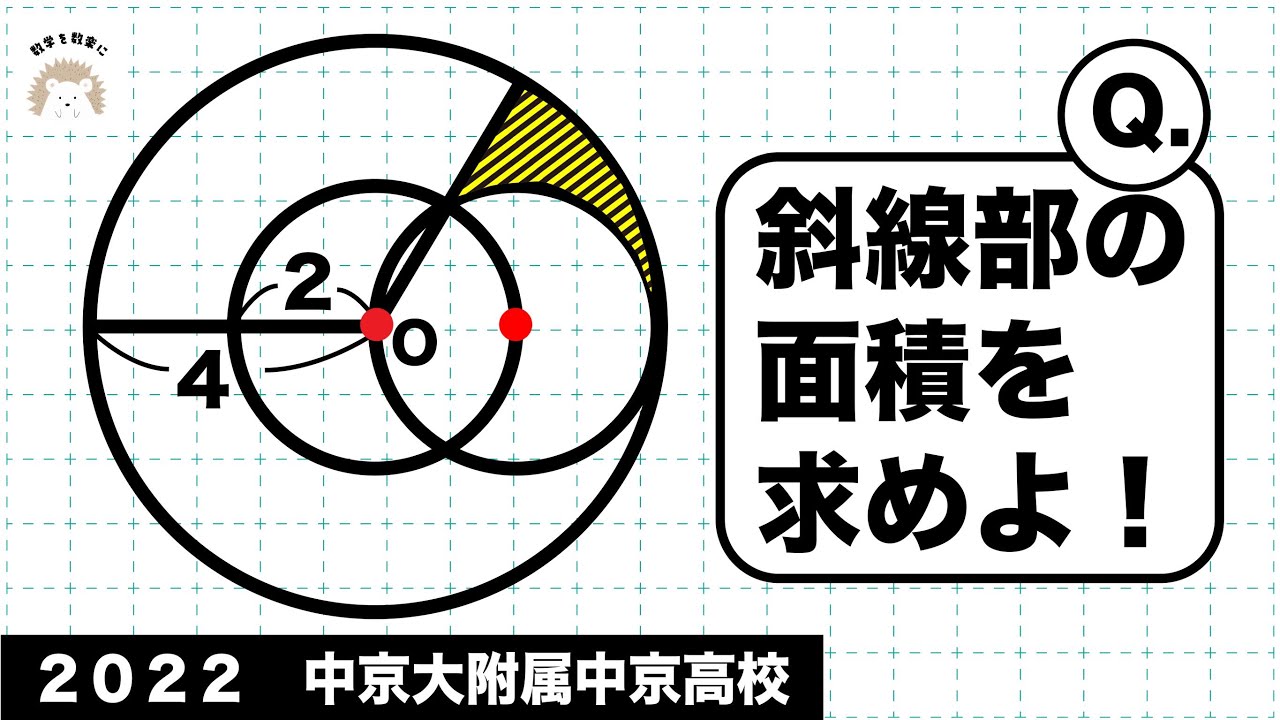
斜線部の面積 中京大附属中京 2022入試問題解説100問解説59問目!
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積を求めよ。
*図は動画内参照
2022中京大学附属中京高等学校
この動画を見る
斜線部の面積を求めよ。
*図は動画内参照
2022中京大学附属中京高等学校
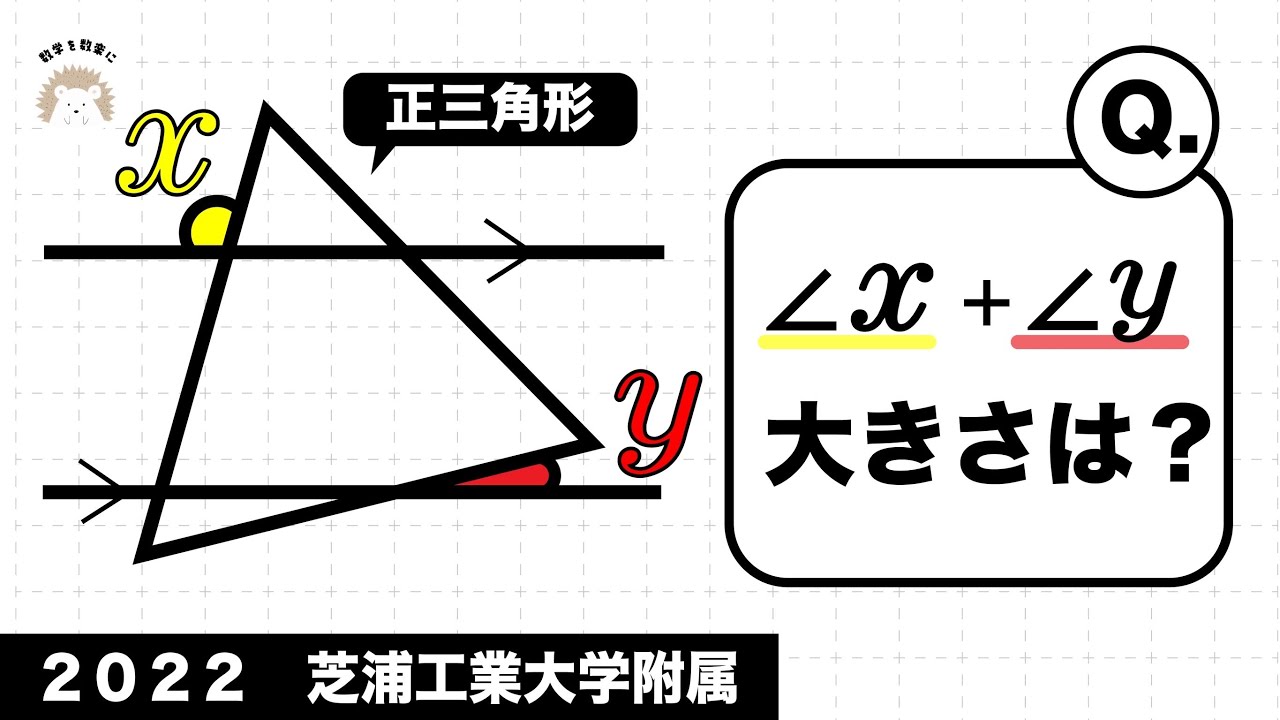
平行線と角の和 芝浦工大附属 2022年入試問題解説46問目
単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x+ \angle y$=?
*図は動画内参照
2022芝浦工業大学附属高等学校
この動画を見る
$\angle x+ \angle y$=?
*図は動画内参照
2022芝浦工業大学附属高等学校
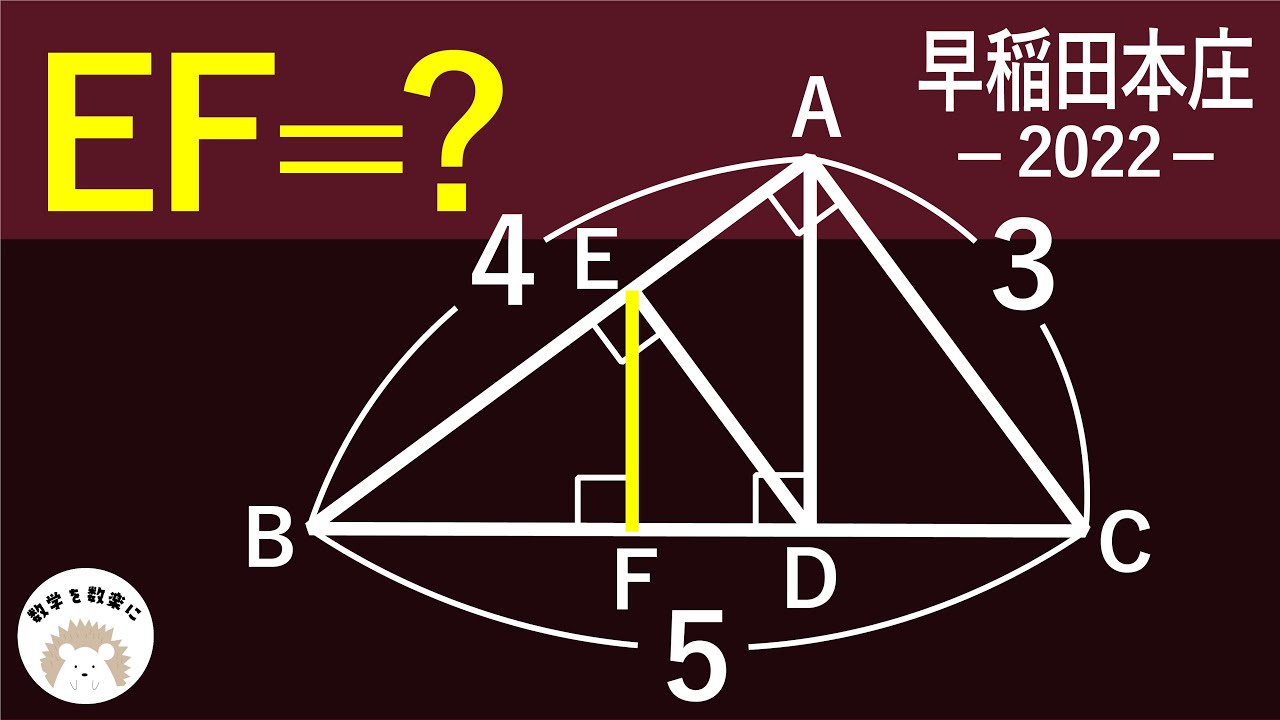
直角三角形たくさん! 早稲田本庄 2022 入試問題解説39問目
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
EF=?
*図は動画内参照
2022早稲田大学本庄高等学院
この動画を見る
EF=?
*図は動画内参照
2022早稲田大学本庄高等学院
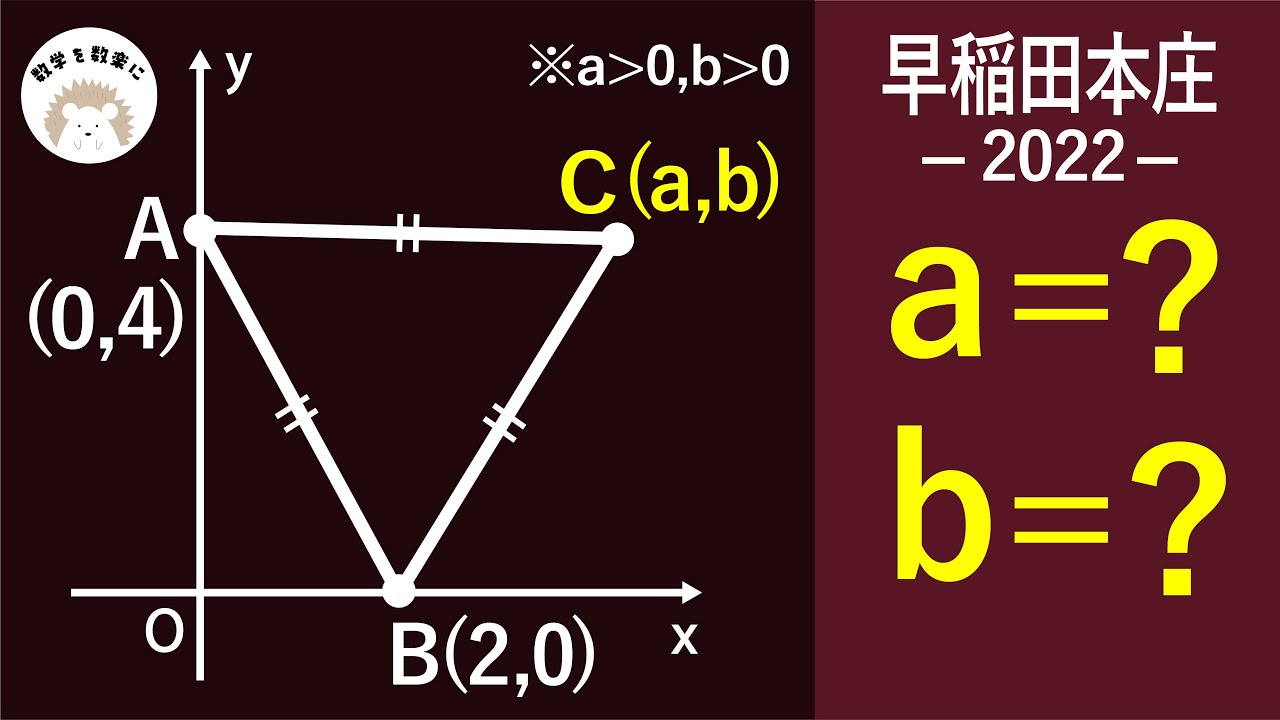
2022年2月9日 早稲田本庄 2022 入試問題解説37問目
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a=?
b=?
(a>0,b>0)
*図は動画内参照
2022早稲田大学本庄高等学院
この動画を見る
a=?
b=?
(a>0,b>0)
*図は動画内参照
2022早稲田大学本庄高等学院
