 約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
 約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
整数問題 基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2P^4-P^2+16$が平方数となるような素数$P$をすべて求めよ.
この動画を見る
$2P^4-P^2+16$が平方数となるような素数$P$をすべて求めよ.
特殊な方程式

【経験することが何よりも大切!】整数:和歌山県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{\dfrac{20}{n}}$の値が自然数となるような自然数$n$をすべて求めなさい.
和歌山県高校過去問
この動画を見る
$ \sqrt{\dfrac{20}{n}}$の値が自然数となるような自然数$n$をすべて求めなさい.
和歌山県高校過去問
絶対に取りたい整数問題!分からない時はとにかく実験あるのみ【早稲田大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n^2+1,2n^2+3,6n^2+5$がすべて素数となる自然数$n$は$n=1,2$のみであることを示せ。
早稲田大過去問
この動画を見る
$n^2+1,2n^2+3,6n^2+5$がすべて素数となる自然数$n$は$n=1,2$のみであることを示せ。
早稲田大過去問
ハルハル様の作成問題④ #整数問題 【難】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(x^3+1)^3+(x^2+1)^2=2^y$を満たす整数の組$(x,y)$をすべて求めよ。
この動画を見る
$(x^3+1)^3+(x^2+1)^2=2^y$を満たす整数の組$(x,y)$をすべて求めよ。
絶対値 中1も解ける!! 海星高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ある整数xの絶対値が4より小さいという。
xは全部でいくつの整数が考えられるか。
海星高校
この動画を見る
ある整数xの絶対値が4より小さいという。
xは全部でいくつの整数が考えられるか。
海星高校
福田の数学〜早稲田大学2022年教育学部第2問〜サイコロの目の積の約数の個数と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$サイコロをn回投げて出た目の積をSとする。Sの正の約数の個数がk個となる
確率を$P_k$とする。次の問いに答えよ。
(1)$P_3$を$n$の式で表せ。
(1)$P_4$を$n$の式で表せ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{2}}$サイコロをn回投げて出た目の積をSとする。Sの正の約数の個数がk個となる
確率を$P_k$とする。次の問いに答えよ。
(1)$P_3$を$n$の式で表せ。
(1)$P_4$を$n$の式で表せ。
2022早稲田大学教育学部過去問
7で割ったあまり 札幌大谷

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
この動画を見る
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
変形できるかできないかが分かれ目 聖望学園

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{6 \sqrt n}{n}$が自然数となる自然数nは何個?
聖望学園高等学校
この動画を見る
$\frac{6 \sqrt n}{n}$が自然数となる自然数nは何個?
聖望学園高等学校
普通の中学生が解くには難しい 興南高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
5つの数字0,1,2,6,7から異なる3つの数字を選び、並べて3ケタの数を作とき
5で割ると2余る数は何個できるか?
興南高等学校
この動画を見る
5つの数字0,1,2,6,7から異なる3つの数字を選び、並べて3ケタの数を作とき
5で割ると2余る数は何個できるか?
興南高等学校
整数問題 海星高校(長崎)
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
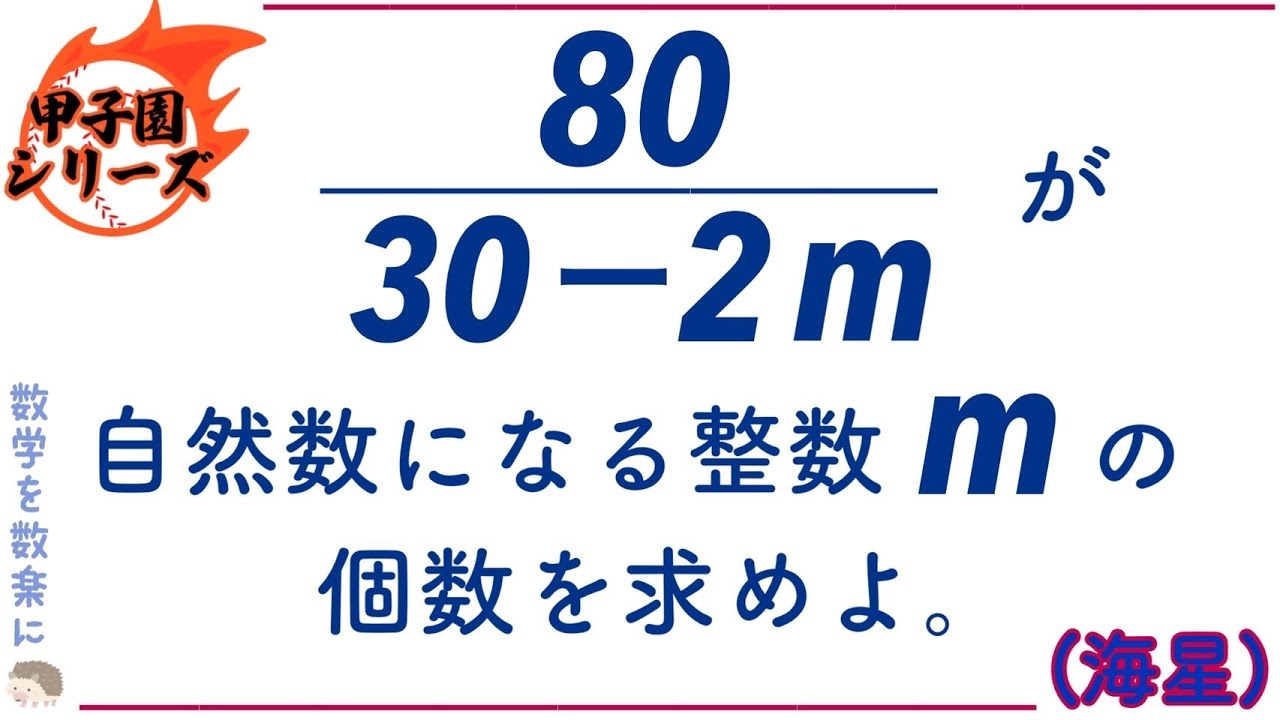
$\frac{80}{30 - 2m}$が自然数になる整数mの個数を求めよ。
海星高校
この動画を見る
$\frac{80}{30 - 2m}$が自然数になる整数mの個数を求めよ。
海星高校
整数問題
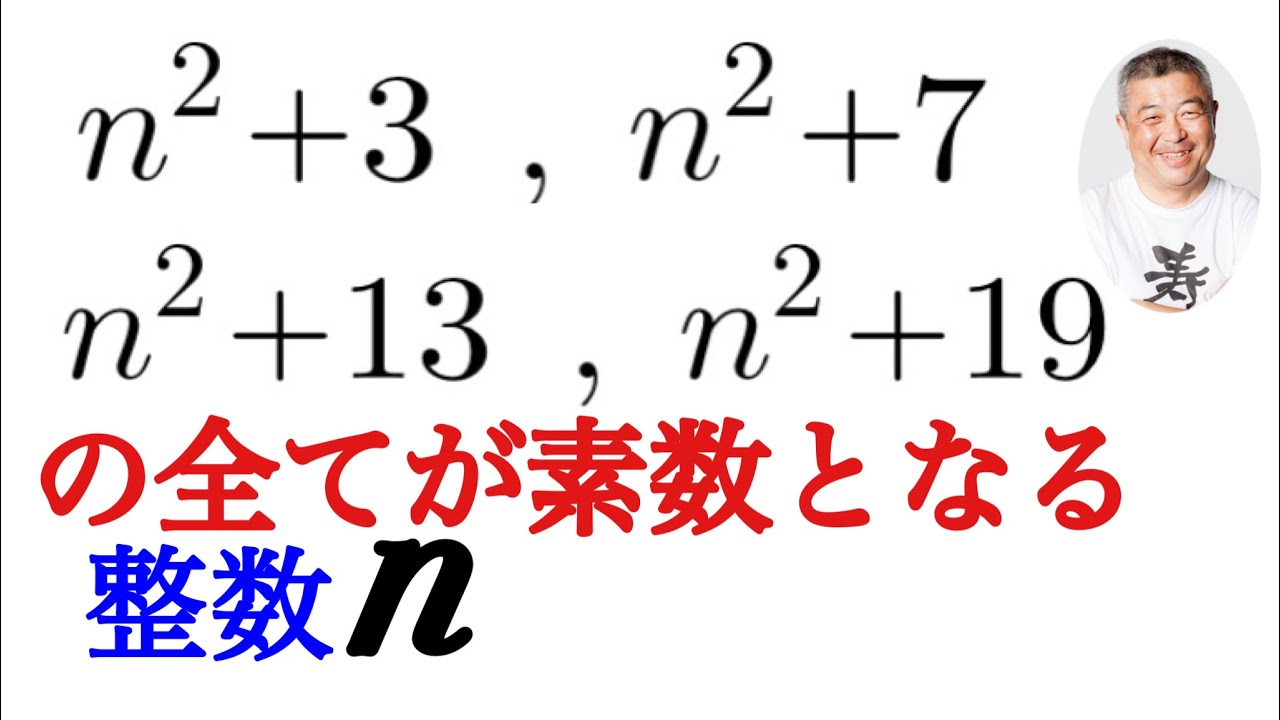
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2+3,n^2+7,n^2+13,n^2+19$のすべてが素数となる整数nをすべて求めよ.
この動画を見る
$ n^2+3,n^2+7,n^2+13,n^2+19$のすべてが素数となる整数nをすべて求めよ.
ただの分数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{3}{m}+\dfrac{4}{n}=\dfrac{1}{12}$,自然数(m,n)をすべて求めよ.
ただし,$\dfrac{3}{m},\dfrac{4}{m}$は既約分数である.
この動画を見る
$ \dfrac{3}{m}+\dfrac{4}{n}=\dfrac{1}{12}$,自然数(m,n)をすべて求めよ.
ただし,$\dfrac{3}{m},\dfrac{4}{m}$は既約分数である.
素数になる2次式

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2-54n+504$が素数となる自然数nをすべて求めよ.
この動画を見る
$ n^2-54n+504$が素数となる自然数nをすべて求めよ.
整数問題が苦手な人必見!大事な考えが詰まった良問!【お茶の水女子大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$k^2+2$が素数となるような素数$k$をすべて見つけよ。また,それ以外にないことを示せ。
(2)整数$l$が5で割り切れないとき,$l^4-1$が5で割り切れることを示せ。
お茶の水女子大過去問
この動画を見る
(1)$k^2+2$が素数となるような素数$k$をすべて見つけよ。また,それ以外にないことを示せ。
(2)整数$l$が5で割り切れないとき,$l^4-1$が5で割り切れることを示せ。
お茶の水女子大過去問
素数製造マシーン 素数とならないものを答えよ 洛星(改)

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$p=n^2+n+41$
100以下の自然数nのうちpが素数とならないものを2つ答えよ
洛星高等学校(改)
この動画を見る
$p=n^2+n+41$
100以下の自然数nのうちpが素数とならないものを2つ答えよ
洛星高等学校(改)
【数A】なんと1分で求められる!?一橋2020大問1(1)10の10乗を2020で割ったあまりを求める

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
10の10乗を2020で割ったあまりを求めよ
この動画を見る
10の10乗を2020で割ったあまりを求めよ
ガウス記号の二次方程式

素数にならないのはなぜ? 洛星

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$N=n^2+n+40$のnにどのような自然数を代入してもNは素数にはならない。
なぜ?
洛星高等学校(改)
この動画を見る
$N=n^2+n+40$のnにどのような自然数を代入してもNは素数にはならない。
なぜ?
洛星高等学校(改)
階乗に関する問題!! 24で割った余り

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
1!+2!+3!+・・・+2022!
24で割った余りは?
この動画を見る
1!+2!+3!+・・・+2022!
24で割った余りは?
整数問題 3乗になる数!! 新潟明訓

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1872 - 36nがある正の整数の3乗で表されるような正の整数nをすべて求めよ
新潟明訓高等学校
この動画を見る
1872 - 36nがある正の整数の3乗で表されるような正の整数nをすべて求めよ
新潟明訓高等学校
整数問題!無限降下法を用いた証明!【数学 入試問題】【千葉大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$が3以上の整数のとき,$x^n+2y^n=4z^n$を満たす自然数$x,y,z$は存在しないことを証明せよ。
千葉大過去問
この動画を見る
$n$が3以上の整数のとき,$x^n+2y^n=4z^n$を満たす自然数$x,y,z$は存在しないことを証明せよ。
千葉大過去問
【数A】modの計算法則を分かりやすく説明します

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
modの計算法則をわかりやすく説明します。(証明付き!)
この動画を見る
modの計算法則をわかりやすく説明します。(証明付き!)
面白不等式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nは自然数である.
$\dfrac{57}{158}\lt \dfrac{m}{n}\lt \dfrac{25}{68}$
mの最小値を求めよ.
この動画を見る
m,nは自然数である.
$\dfrac{57}{158}\lt \dfrac{m}{n}\lt \dfrac{25}{68}$
mの最小値を求めよ.
福田の数学〜早稲田大学2022年理工学部第2問〜条件を満たすm個の2次関数の積でできる2m次方程式の異なる解の総和

単元:
#数Ⅰ#数A#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
合同式と組み合わせの公式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{30} \mathrm{ C }_{15}$を31で割った余りを求めよ.
この動画を見る
${}_{30} \mathrm{ C }_{15}$を31で割った余りを求めよ.
平方して下3桁が同じ数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次のような自然数をすべて求めよ.
①2桁の自然数を2乗したら下2桁が同じ数を求めよ.
②3桁の自然数を2乗したら下3桁が同じ数を求めよ.
この動画を見る
次のような自然数をすべて求めよ.
①2桁の自然数を2乗したら下2桁が同じ数を求めよ.
②3桁の自然数を2乗したら下3桁が同じ数を求めよ.
福田の数学〜慶應義塾大学2022年看護医療学部第2問(3)〜平方数を3で割った余りに関する論証

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
平方数にならない式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$n(n+1)(n+2)(n+3)$は平方数でないことを示せ.
この動画を見る
nを自然数とする.
$n(n+1)(n+2)(n+3)$は平方数でないことを示せ.
無限降下法って知ってる?整数問題の難問です【数学 入試問題】【九州大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
この動画を見る
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
