ユークリッド互除法と不定方程式・Ｎ進法
ユークリッド互除法と不定方程式・Ｎ進法
福田のおもしろ数学364〜2次の不定方程式の整数解が無数に存在することの証明
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2+y^2+z^2=(x-y)(y-z)(z-x)$ を満たす整数の組 $(x,y,z)$ は無数に存在することを証明せよ。
この動画を見る
$x^2+y^2+z^2=(x-y)(y-z)(z-x)$ を満たす整数の組 $(x,y,z)$ は無数に存在することを証明せよ。
福田のおもしろ数学355〜3次の不定方程式の解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x,y$ は $0$ 以上の整数で、$y^3=x^3+8x^2-6x+8$ を満たしている。このような $(x,y)$ の組をすべて求めて下さい。
この動画を見る
$x,y$ は $0$ 以上の整数で、$y^3=x^3+8x^2-6x+8$ を満たしている。このような $(x,y)$ の組をすべて求めて下さい。
福田のおもしろ数学321〜不定方程式の整数解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2+y^2+z^2=2xyz$ を満たす整数の組 $(x,y,z)$ は $(0,0,0)$ のみであることを示してください。
この動画を見る
$x^2+y^2+z^2=2xyz$ を満たす整数の組 $(x,y,z)$ は $(0,0,0)$ のみであることを示してください。
福田のおもしろ数学308〜不定方程式の整数解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2+xy+y^2 = (\dfrac{x+y}{3}+1)^3$を満たす整数x、yをすべて求めて下さい。
この動画を見る
$x^2+xy+y^2 = (\dfrac{x+y}{3}+1)^3$を満たす整数x、yをすべて求めて下さい。
福田の数学〜早稲田大学2024教育学部第1問(1)〜2進法による循環小数の表記
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\frac{4}{9}$を2進法の循環小数で表せ。
この動画を見る
$\frac{4}{9}$を2進法の循環小数で表せ。
意外と差がつく！互いに素の証明！できるようになっておきたい【一橋大学】【数学 入試問題】
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
この動画を見る
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
福田の数学〜東京慈恵会医科大学2024医学部第3問〜条件を満たす2次式に関する証明と反例の作成
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
$p$,$q$は互いに素である自然数とする。実数$a$,$b$,$c$に対して、$x$の2次多項式 $f(x)=ax^{ 2 }+bx+c$を考える。 ただし、$a \neq 0$とする。$f(x)$が条件「ある整数$k$について$f(k-1)$, $f(k)$, $f(k + 1)$ は整数となり、$f(x)$は $px-q$で割り切れる」をみたすとき、次の問いに答えよ。
(1) $\frac{2a}{p}$,$\frac{2c}{q}$は整数であることを示せ。
(2) 命題「$f(x)$が上の条件をみたすならば、$\frac{a}{p}$,$\frac{c}{q}$は整数である」は正しいか。正しければそれを示せ。正しくなければ、反例を1つあげよ。
この動画を見る
$p$,$q$は互いに素である自然数とする。実数$a$,$b$,$c$に対して、$x$の2次多項式 $f(x)=ax^{ 2 }+bx+c$を考える。 ただし、$a \neq 0$とする。$f(x)$が条件「ある整数$k$について$f(k-1)$, $f(k)$, $f(k + 1)$ は整数となり、$f(x)$は $px-q$で割り切れる」をみたすとき、次の問いに答えよ。
(1) $\frac{2a}{p}$,$\frac{2c}{q}$は整数であることを示せ。
(2) 命題「$f(x)$が上の条件をみたすならば、$\frac{a}{p}$,$\frac{c}{q}$は整数である」は正しいか。正しければそれを示せ。正しくなければ、反例を1つあげよ。
福田のおもしろ数学270〜3変数の不定方程式の自然数解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の整数 $a,b,c$ で $ (1 + \frac{1}{a})(1+ \frac{1}{b})(1 + \frac{1}{c}) = 2 $ を満たすものをすべて求めよ。
この動画を見る
正の整数 $a,b,c$ で $ (1 + \frac{1}{a})(1+ \frac{1}{b})(1 + \frac{1}{c}) = 2 $ を満たすものをすべて求めよ。
福田の数学〜上智大学2024TEAP利用型理系第1問(1)〜不定方程式の解
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}(1)77x+52y=1$を満たす整数$x$、$y$の組のうち、$x$が正で最小の組は$(x,y)=(\boxed{ア},\boxed{イ})$である。
この動画を見る
$\boxed{1}(1)77x+52y=1$を満たす整数$x$、$y$の組のうち、$x$が正で最小の組は$(x,y)=(\boxed{ア},\boxed{イ})$である。
2進法のかけ算
福田の数学〜東京医科歯科大学2024医学部第1問〜n変数の不定方程式の解
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
$n$を$2$以上の自然数とする。自然数の組$(a_1,a_2,\cdots,a_n)$を解とする方程式
$(*)~a_1+a_2+\cdots+a_n=a_1 \times a_2 \times \cdots \times a_n$を考える。
(1) $n=3$のとき、$(*)$の解$(a_1,a_2,a_3)$のうち、$a_1\leqq a_2 \leqq a_3$を満たすものをすべて求めよ。
(2) $n\geqq 3$のとき、$(*)$の任意の解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$が少なくとも1つ存在することを示せ。
(3) $(*)$のある解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$がちょうど2個存在しているとする。このとき、$n$のとりうる値を全て求めよ。
この動画を見る
$n$を$2$以上の自然数とする。自然数の組$(a_1,a_2,\cdots,a_n)$を解とする方程式
$(*)~a_1+a_2+\cdots+a_n=a_1 \times a_2 \times \cdots \times a_n$を考える。
(1) $n=3$のとき、$(*)$の解$(a_1,a_2,a_3)$のうち、$a_1\leqq a_2 \leqq a_3$を満たすものをすべて求めよ。
(2) $n\geqq 3$のとき、$(*)$の任意の解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$が少なくとも1つ存在することを示せ。
(3) $(*)$のある解$(a_1,a_2,\cdots,a_n)$において、$a_i=1$となる$i$がちょうど2個存在しているとする。このとき、$n$のとりうる値を全て求めよ。
答え方が困る？？ 整数問題 （高校数学です）
福田のおもしろ数学208〜必要条件で絞って十分で切り返す
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
この動画を見る
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
福田のおもしろ数学203〜整数を取る4変数の最大値
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c,d$はすべて正の整数とする。
$a+b+c+d=63$のとき$ab+bc+cd$の最大値を求めよ。
この動画を見る
$a,b,c,d$はすべて正の整数とする。
$a+b+c+d=63$のとき$ab+bc+cd$の最大値を求めよ。
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
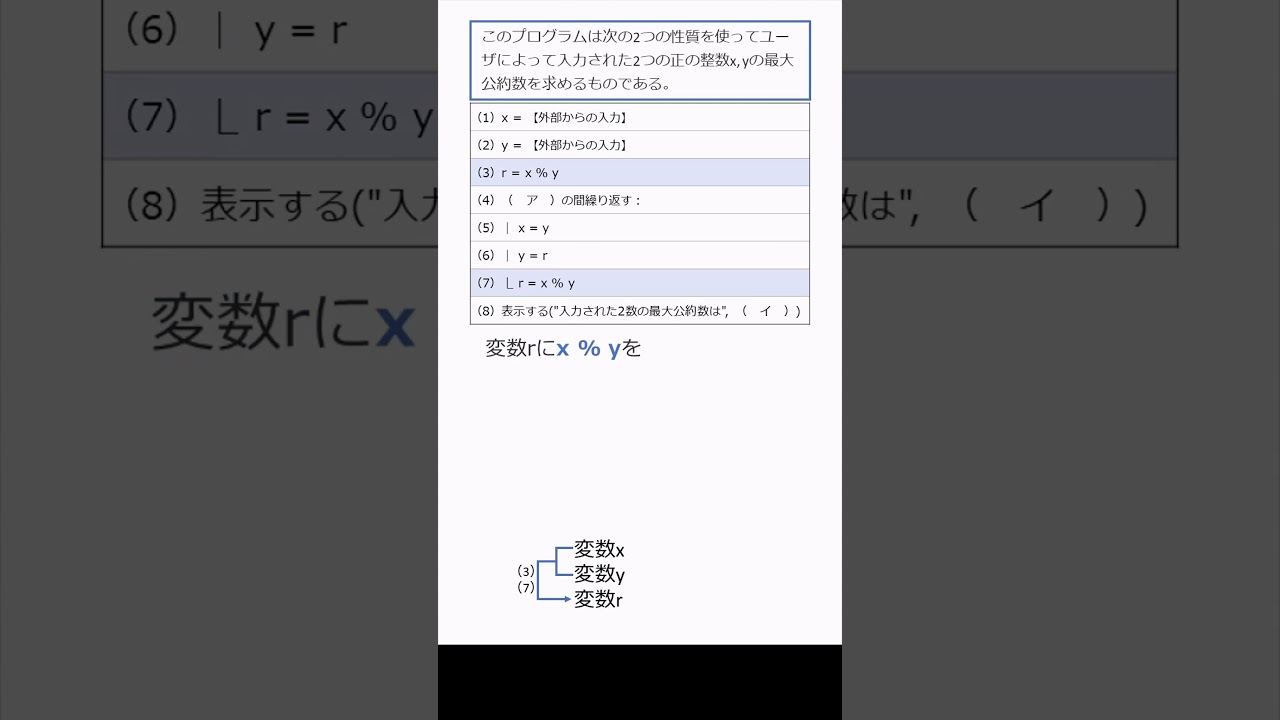
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
この動画を見る
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
この動画を見る
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
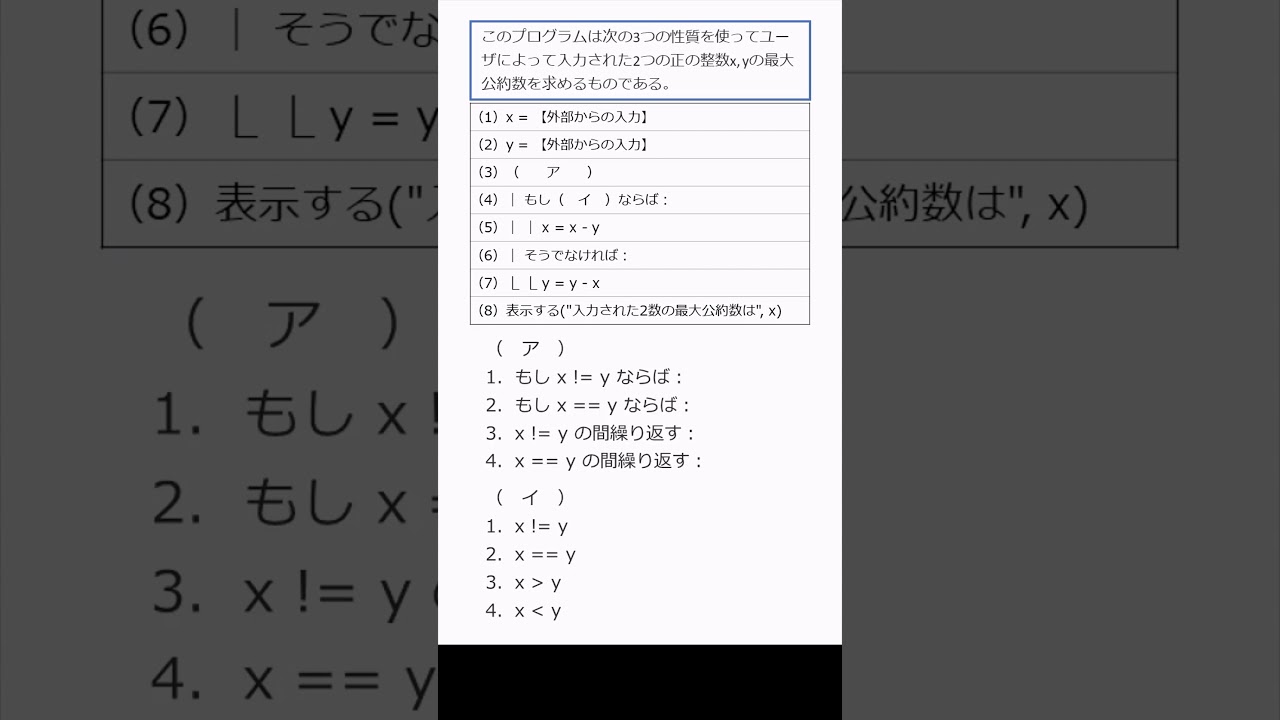
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
この動画を見る
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
この動画を見る
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
福田の数学〜慶應義塾大学2024年経済学部第1問(1)〜2次方程式が整数解をもつ条件
単元：
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$－($p$－9)$x$－$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$－($p$－9)$x$－$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
福田のおもしろ数学147〜3変数の不定方程式の一般解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
35x+91y+65z=3 を満たす整数x, y, zを求めよ。
この動画を見る
35x+91y+65z=3 を満たす整数x, y, zを求めよ。
方程式
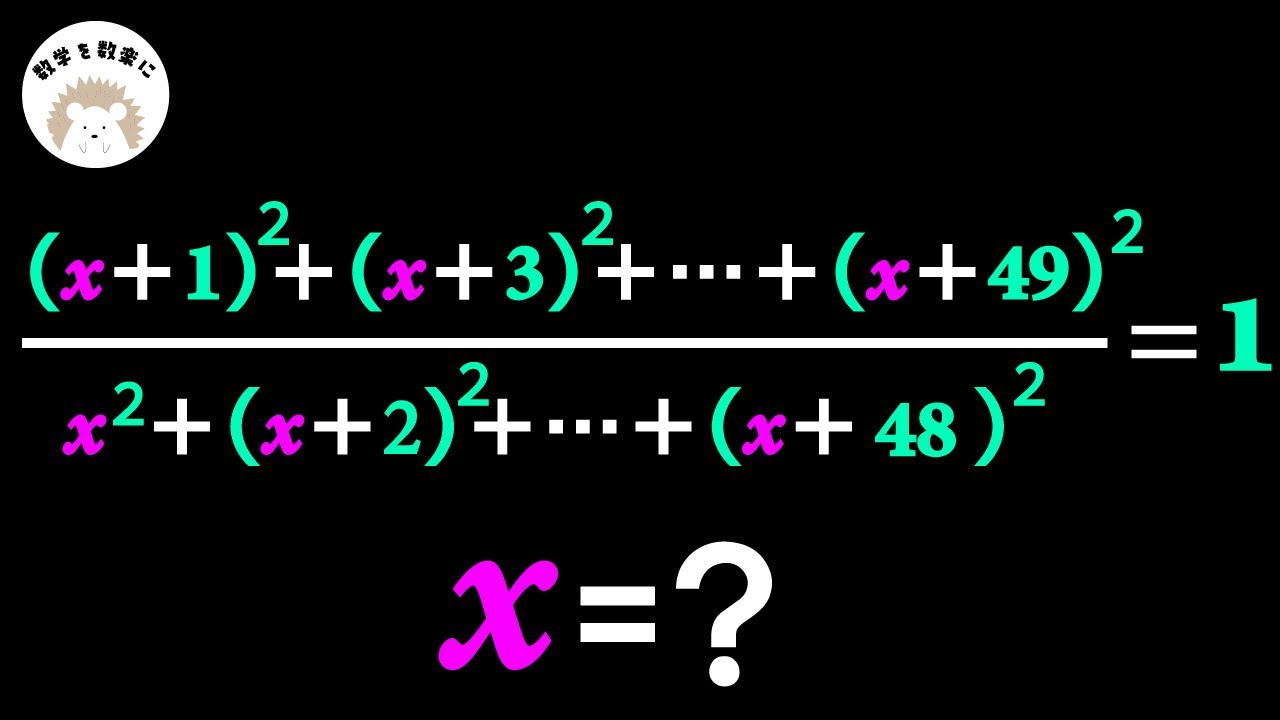
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\frac{(x+1)^2+(x+3)^2+(x+5)^2+ \cdots +(x+49)^2}{x^2+(x+2)^2+(x+4)^2+ \cdots +(x+48)^2}=1$
この動画を見る
$\frac{(x+1)^2+(x+3)^2+(x+5)^2+ \cdots +(x+49)^2}{x^2+(x+2)^2+(x+4)^2+ \cdots +(x+48)^2}=1$
福田の数学〜慶應義塾大学2024年商学部第1問(3)〜不定方程式の自然数解
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$
(3)$a$<$b$<$c$かつ $\displaystyle\frac{1}{a}$+$\displaystyle\frac{2}{b}$+$\displaystyle\frac{3}{c}$=$2$ を満たす自然数の組($a$, $b$, $c$)をすべて求めよ。
この動画を見る
$\Large\boxed{1}$
(3)$a$<$b$<$c$かつ $\displaystyle\frac{1}{a}$+$\displaystyle\frac{2}{b}$+$\displaystyle\frac{3}{c}$=$2$ を満たす自然数の組($a$, $b$, $c$)をすべて求めよ。
いやらしい方程式を解け！！
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
(1)$x=x$
(2)$x=x+1$
この動画を見る
方程式を解け
(1)$x=x$
(2)$x=x+1$
福田のおもしろ数学084〜85をいくつかの和で一意的に表す
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
85は7つの数
1,2,4,8,16,32,64
のいくつかの和としてただ1通りに表されることを示せ。
この動画を見る
85は7つの数
1,2,4,8,16,32,64
のいくつかの和としてただ1通りに表されることを示せ。
京都大 2024文系数学
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
ある自然数を八進法,九進法,十進法で表したら桁数が同じ最大の自然数は？
$0.3010<\log_{10}{3}<0.3011$
$0.4771<\log_{10}{2}<0.4772$
2024京都大過去問
この動画を見る
ある自然数を八進法,九進法,十進法で表したら桁数が同じ最大の自然数は？
$0.3010<\log_{10}{3}<0.3011$
$0.4771<\log_{10}{2}<0.4772$
2024京都大過去問
東大 文系数学 2024
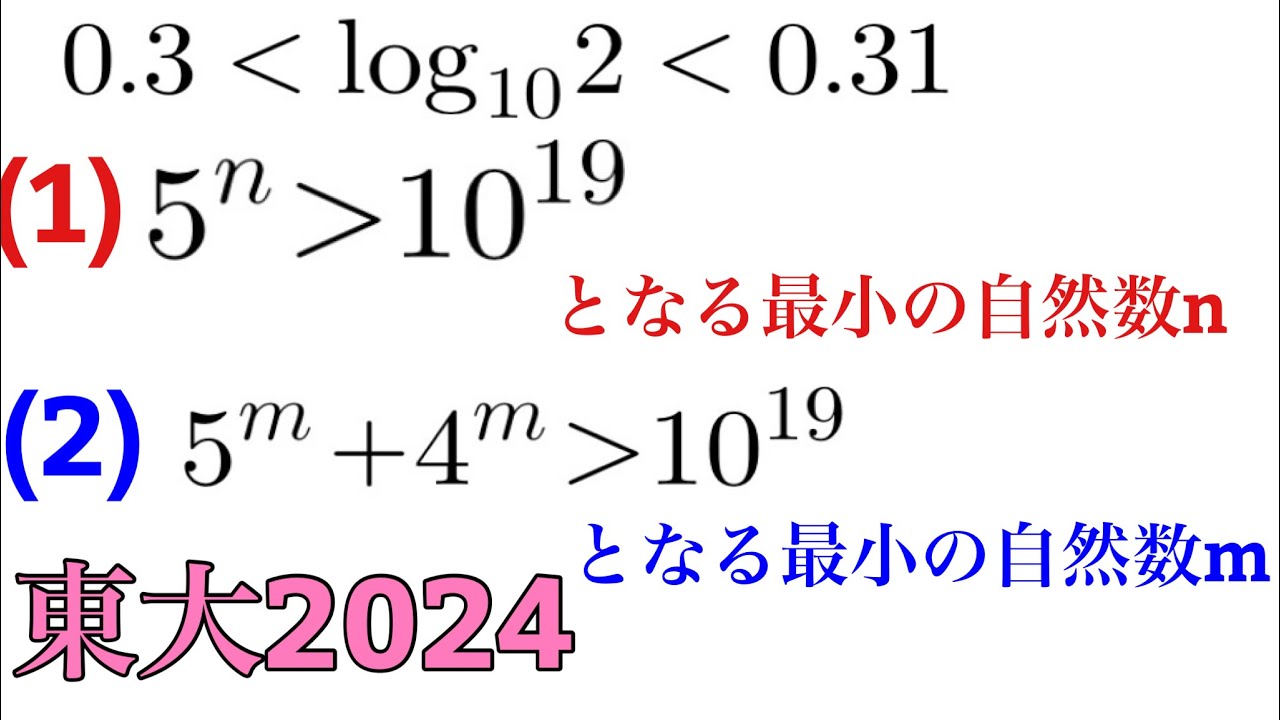
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0.3＜\log_{10}{2}＜0.31$
を用いてよい
(1)$5^n>10^{19}$
となる最小の自然数n
(2)$5^m+4^m>10^{19}$
となる最小の自然数m
2024東大文系過去問
この動画を見る
$0.3＜\log_{10}{2}＜0.31$
を用いてよい
(1)$5^n>10^{19}$
となる最小の自然数n
(2)$5^m+4^m>10^{19}$
となる最小の自然数m
2024東大文系過去問
どんな約分にも使える裏技「よこよこ法」を教育系インフルエンサーに教えました【ラオ先生×まさし×あきとんとん】
単元：
#算数(中学受験)#計算と数の性質#数の性質その他#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
（1）$\displaystyle \frac{51}{68}$
（2）$\displaystyle \frac{161}{115}$
（3）$\displaystyle \frac{5080}{5207}$
この動画を見る
（1）$\displaystyle \frac{51}{68}$
（2）$\displaystyle \frac{161}{115}$
（3）$\displaystyle \frac{5080}{5207}$
2進法ののび太ってなに？
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
二進法ののび太を使って二進法の原理を解説をします。
この動画を見る
二進法ののび太を使って二進法の原理を解説をします。
福田の数学〜東京大学2018年理系第2問〜数列の増減とユークリッドの互除法
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a_{ 1 },a_{ 2 }・・・$を
$a_{ n }=\dfrac{2_{ n }+{}_1 \mathrm{ C }_n}{n!}$(n=1,2,・・・)
で定める
(1)$n \geqq 2$とする。$\dfrac{a_{n}}{a_{n-1}}$を規約分数$\dfrac{q_{n}}{p_{n}}$として表したときの分母$p_{n} \geqq 1$と分子$q_{n}$を求めよ。
(2)$a_{n}$が整数となる$n\geqq1$をすべて求めよ。
2018東京大学理過去問
この動画を見る
$a_{ 1 },a_{ 2 }・・・$を
$a_{ n }=\dfrac{2_{ n }+{}_1 \mathrm{ C }_n}{n!}$(n=1,2,・・・)
で定める
(1)$n \geqq 2$とする。$\dfrac{a_{n}}{a_{n-1}}$を規約分数$\dfrac{q_{n}}{p_{n}}$として表したときの分母$p_{n} \geqq 1$と分子$q_{n}$を求めよ。
(2)$a_{n}$が整数となる$n\geqq1$をすべて求めよ。
2018東京大学理過去問
福田のおもしろ数学044〜みんな苦手なn進法〜10進法と5進法で同じ桁数になる数
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
10 進法で表しても、 5 進法で表しても、桁数が変わらない正の整数は何個あるか。
この動画を見る
10 進法で表しても、 5 進法で表しても、桁数が変わらない正の整数は何個あるか。