ユークリッド互除法と不定方程式・Ｎ進法
ユークリッド互除法と不定方程式・Ｎ進法
福田の数学〜九州大学2022年理系第３問〜約数と倍数と不定方程式の自然数解
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
この動画を見る
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
福田の数学〜神戸大学2022年文系第３問〜指数方程式と整数解
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$を実数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)$m,n$を$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{5}$とする。$m,n$の値を求めよ。
(3)$m,n$を自然数とし、$a^m=b^n=(ab)^5$とする。bの値をaを用いて表せ。
2022神戸大学文系過去問
この動画を見る
$a,b$を実数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)$m,n$を$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{5}$とする。$m,n$の値を求めよ。
(3)$m,n$を自然数とし、$a^m=b^n=(ab)^5$とする。bの値をaを用いて表せ。
2022神戸大学文系過去問
福田の数学〜神戸大学2022年理系第５問〜指数方程式と整数解
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
a,bを実数、$p$を素数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)m,nを$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{p}$とする。m,nの値をpを用いて表せ。
(3)m,nを自然数とし、$a^m=b^n=(ab)^p$とする。bの値をa,pを用いて表せ。
2022神戸大学理系過去問
この動画を見る
a,bを実数、$p$を素数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)m,nを$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{p}$とする。m,nの値をpを用いて表せ。
(3)m,nを自然数とし、$a^m=b^n=(ab)^p$とする。bの値をa,pを用いて表せ。
2022神戸大学理系過去問
【不定方程式の特解はこれで楽勝】合同式を使った不定方程式の解き方を解説！〔数学 高校数学〕
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
合同式を使った不定方程式の解き方について解説します。
この動画を見る
合同式を使った不定方程式の解き方について解説します。
福田の数学〜東京工業大学2022年理系第２問〜３つの数の最大公約数
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
この動画を見る
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
福田の数学・入試問題解説〜東北大学2022年理系第１問〜不定方程式の整数解の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
Kを3より大きい奇数とし、$l+m+n=K$を満たす正の奇数の組(l,m,n)
の個数Nを考える。ただし、例えば、$K=5$のとき、$(l,m,n)=(1,1,3)$
と$(l,m,n)=(1,3,1)$とは異なる組とみなす。
(1)$K=99$のとき、Nを求めよ。
(2)$K=99$のとき、l,m,nの中に同じ奇数を2つ以上含む組(l,m,n)の個数を
求めよ。
(3)$N \gt K$を満たす最小のKを求めよ。
2022東北大学理系過去問
この動画を見る
Kを3より大きい奇数とし、$l+m+n=K$を満たす正の奇数の組(l,m,n)
の個数Nを考える。ただし、例えば、$K=5$のとき、$(l,m,n)=(1,1,3)$
と$(l,m,n)=(1,3,1)$とは異なる組とみなす。
(1)$K=99$のとき、Nを求めよ。
(2)$K=99$のとき、l,m,nの中に同じ奇数を2つ以上含む組(l,m,n)の個数を
求めよ。
(3)$N \gt K$を満たす最小のKを求めよ。
2022東北大学理系過去問
福田の数学〜京都大学2022年理系第３問〜３つの数の最大公約数
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
nを自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
2022京都大学理系過去問
この動画を見る
nを自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
2022京都大学理系過去問
不定方程式
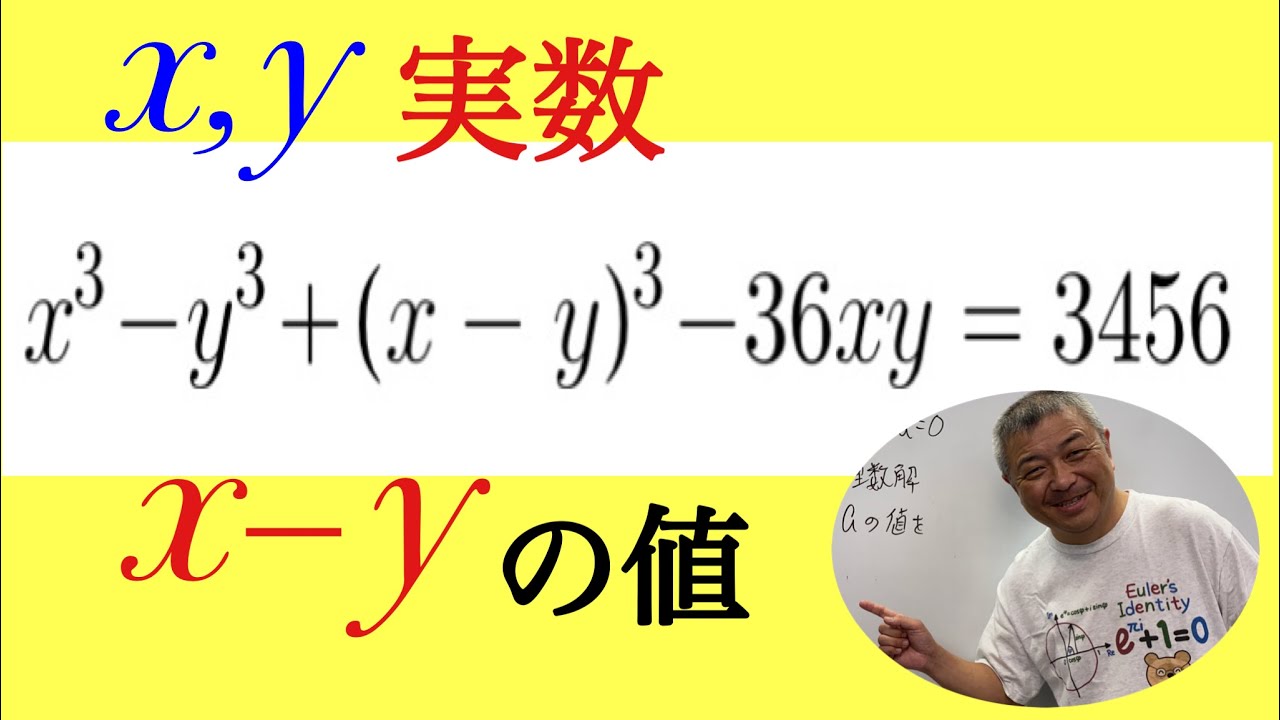
単元：
#数A#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
この動画を見る
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
【数学A/整数】 n進法→10進法（小数）
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の数を10進法の小数で表せ。
（1）$0.101_{(2)}$
（2）$0.24_{(5)}$
この動画を見る
次の数を10進法の小数で表せ。
（1）$0.101_{(2)}$
（2）$0.24_{(5)}$
【数学A/整数】10進法をn進法で表す
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の10進法を[ ]内の表し方で表せ。
（1）57 [2進法]
（2）83 [5進法]
この動画を見る
次の10進法を[ ]内の表し方で表せ。
（1）57 [2進法]
（2）83 [5進法]
◆わかりやすく◆数学A・整数 n進法を10進法で表す
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の数を10進法で表せ。
（1）$1101_{(2)}$
（2）$231_{(4)}$
この動画を見る
次の数を10進法で表せ。
（1）$1101_{(2)}$
（2）$231_{(4)}$
【わかりやすく解説】等式を満たす自然数を求める（数学A・整数）
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
等式$3x+4y=45$を満たす自然数$x,y$の組を全て求めよ。
この動画を見る
等式$3x+4y=45$を満たす自然数$x,y$の組を全て求めよ。
【テストによく出る】数学A 一次不定方程式（ユークリッドの互除法を使って特殊解を求める）
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
不定方程式$90x-37y=1$の整数解を求めよ。
この動画を見る
不定方程式$90x-37y=1$の整数解を求めよ。
【0から理解できる】一次不定方程式を解説しました！（数学A・整数）
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の不定方程式の整数解を求めよ。
（1）$5x-3y=1$
（2）$5x-3y=4$
この動画を見る
次の不定方程式の整数解を求めよ。
（1）$5x-3y=1$
（2）$5x-3y=4$
【数学A/整数】ユークリッドの互除法（文字式）
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
$7n+6$と$2n+3$の最大公約数が$3$になるような$20$以下の自然数$n$をすべて求めよ。
この動画を見る
$7n+6$と$2n+3$の最大公約数が$3$になるような$20$以下の自然数$n$をすべて求めよ。
【数学A/整数】ユークリッドの互除法
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
1207と994の最大公約数を、ユークリッドの互除法を用いて求めよ。
この動画を見る
1207と994の最大公約数を、ユークリッドの互除法を用いて求めよ。
不定方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
整数$(x,y)$を求めよ.
$x^2y+7x-2xy=15$
この動画を見る
整数$(x,y)$を求めよ.
$x^2y+7x-2xy=15$
2022共通テスト 数１A １次不定方程式
【高校数学】1次不定方程式例題演習～応用例題～ 5-9.5【数学Ａ】
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
6で割ると1余り、11で割ると5余るような自然数のうち3桁で最小のものを求めよ。
この動画を見る
6で割ると1余り、11で割ると5余るような自然数のうち3桁で最小のものを求めよ。
不定方程式の解き方
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
不定方程式の解の求め方説明動画です
この動画を見る
不定方程式の解の求め方説明動画です
【高校数学】1次不定方程式～自分に合った解き方を身に付けよう～ 5-9【数学A】
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$45x+32y=4$の整数解をすべて求めよ
この動画を見る
$45x+32y=4$の整数解をすべて求めよ
独協医大 n進法
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0.2_{(a)}=0.12_{(b)}$
$a,b$の値を求めよ.
独協医大過去問
この動画を見る
$0.2_{(a)}=0.12_{(b)}$
$a,b$の値を求めよ.
独協医大過去問
指数方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$27^x-2・18^x+12^x=8^{x+\frac{1}{3}}$
この動画を見る
実数解を求めよ.
$27^x-2・18^x+12^x=8^{x+\frac{1}{3}}$
変な指数方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
この動画を見る
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
指数方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
この動画を見る
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
変な方程式 指数タワー
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
この動画を見る
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
変な指数方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
この動画を見る
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
指数方程式 答えは１つじゃないよ
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
この動画を見る
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
この動画を見る
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
未知数２で式１つの方程式
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
この動画を見る
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$