 整数の性質
整数の性質
 整数の性質
整数の性質
13奈良県教員採用試験(数学:1-1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
この動画を見る
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
15奈良県教員採用試験(数学:中-4番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
この動画を見る
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
灘中 難関大学並の整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A=123456789$
$A$の2つの数を入れかえてできる数を小さい順に$a_1,a_2・・・・・・a_{36}$とする.
$a_1=123456798$
$a_{36}=923456781$
$b_k=a_k-A,1\leqq k\leqq 36$である.
(1)$1000$で割り切れる$b_k$の個数を求めよ.
(2)$37$で割り切れる$b_k$の個数を求めよ.
(3)$b_1 \times b_2 \times b_3 \times ・・・\times b_{36}$は3で何回割り切れるか
2016灘中過去問
この動画を見る
$A=123456789$
$A$の2つの数を入れかえてできる数を小さい順に$a_1,a_2・・・・・・a_{36}$とする.
$a_1=123456798$
$a_{36}=923456781$
$b_k=a_k-A,1\leqq k\leqq 36$である.
(1)$1000$で割り切れる$b_k$の個数を求めよ.
(2)$37$で割り切れる$b_k$の個数を求めよ.
(3)$b_1 \times b_2 \times b_3 \times ・・・\times b_{36}$は3で何回割り切れるか
2016灘中過去問
小樽商科大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{2n-2}{n^2+2n+2}$が整数となる整数$n$を求めよ.
2018小樽商科大過去問
この動画を見る
$\dfrac{2n-2}{n^2+2n+2}$が整数となる整数$n$を求めよ.
2018小樽商科大過去問
信州大2020 指数方程式の解の存在条件

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$9^x-k(3^x+3^{-x})+9^{-x}+\dfrac{k^2}{4}+k-17=0$
が実数解をもつ$k$の範囲を求めよ.
2020信州大過去問
この動画を見る
$9^x-k(3^x+3^{-x})+9^{-x}+\dfrac{k^2}{4}+k-17=0$
が実数解をもつ$k$の範囲を求めよ.
2020信州大過去問
16神奈川県教員採用試験(数学:整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
パスラボ宇佐見さん登場 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$7^n=k^2-99$
整数$k,n$を全て求めよ.
この動画を見る
$7^n=k^2-99$
整数$k,n$を全て求めよ.
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^a+m^2=n^4$
$a,m,n$は自然数で,$m,n$は奇数であることを示せ.
この動画を見る
$2^a+m^2=n^4$
$a,m,n$は自然数で,$m,n$は奇数であることを示せ.
熊本大2020整数問題
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+5y^2=2z^2$を満たす自然数$(x,y,z)$は存在しないことを示せ.
2020熊本大過去問
この動画を見る
$x^2+5y^2=2z^2$を満たす自然数$(x,y,z)$は存在しないことを示せ.
2020熊本大過去問
広島大 約数の総和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は0以上の整数である.
$3^{2m+1}・7^{2n+1}$の正の約数のうち,4で割って1余るものの総和を求めよ.
広島大過去問
この動画を見る
$m,n$は0以上の整数である.
$3^{2m+1}・7^{2n+1}$の正の約数のうち,4で割って1余るものの総和を求めよ.
広島大過去問
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^2+2n-1$と$n^5-5$がともに7の倍数となる$n$のうち3桁で最小のものを求めよ.
この動画を見る
$n^2+2n-1$と$n^5-5$がともに7の倍数となる$n$のうち3桁で最小のものを求めよ.
14兵庫県教員採用試験(数学:1-1番 整数問題)
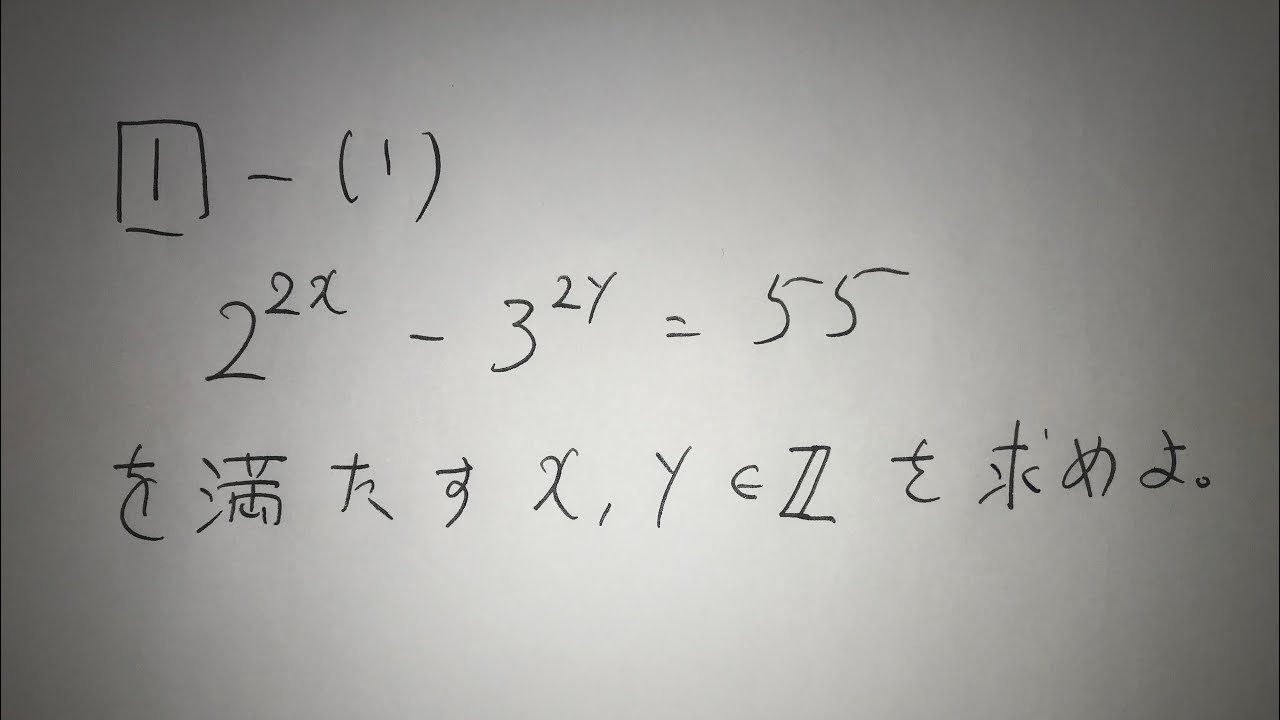
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
この動画を見る
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
東工大 ガウス記号

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は$10000$以下の自然数である.
$[\sqrt{n}]$が$n$の約数となる.$n$は何個あるか.
2012東工大過去問
この動画を見る
$n$は$10000$以下の自然数である.
$[\sqrt{n}]$が$n$の約数となる.$n$は何個あるか.
2012東工大過去問
早稲田大 ガウス記号

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$は実数であり,$n$は自然数である.
①$\left[\dfrac{1}{2}x\right]-\left[\dfrac{1}{2}[x]\right]=0$示せ.
②$\left[\dfrac{1}{n}x\right]-\left[\dfrac{1}{n}[x]\right]=0$を求めよ.
2009早稲田大過去問
この動画を見る
$x$は実数であり,$n$は自然数である.
①$\left[\dfrac{1}{2}x\right]-\left[\dfrac{1}{2}[x]\right]=0$示せ.
②$\left[\dfrac{1}{n}x\right]-\left[\dfrac{1}{n}[x]\right]=0$を求めよ.
2009早稲田大過去問
素数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5m^2+4mn-n^2$が素数となる自然数$(m,n)$は無限にあることを示せ.
この動画を見る
$5m^2+4mn-n^2$が素数となる自然数$(m,n)$は無限にあることを示せ.
大阪府立大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は整数であり,$0\leqq n\leqq m$とする.
①$3m^2+mn-2n^2$が素数となる($m,n$)
②$m^4-3m^2n^2-4n^4-6m^2-16n^2-16$が素数となる$(m,n)$
2019大阪府立大過去問
この動画を見る
$m,n$は整数であり,$0\leqq n\leqq m$とする.
①$3m^2+mn-2n^2$が素数となる($m,n$)
②$m^4-3m^2n^2-4n^4-6m^2-16n^2-16$が素数となる$(m,n)$
2019大阪府立大過去問
高知大(医)整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$(p,q)$の組は何個あるか.
①$p^2-q^2=250$
②$p^2-q^2=210000$
2020高知大(医)過去問
この動画を見る
整数$(p,q)$の組は何個あるか.
①$p^2-q^2=250$
②$p^2-q^2=210000$
2020高知大(医)過去問
お茶の水女子大 不定方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2x+25y=1993$を満たす整数$x,y$のうち,$x$と$y$の差の絶対値が最小となる$x,y$を求めよ.
お茶の水女子大過去問
この動画を見る
$2x+25y=1993$を満たす整数$x,y$のうち,$x$と$y$の差の絶対値が最小となる$x,y$を求めよ.
お茶の水女子大過去問
17東京都教員採用試験(数学1-1番 整数問題)
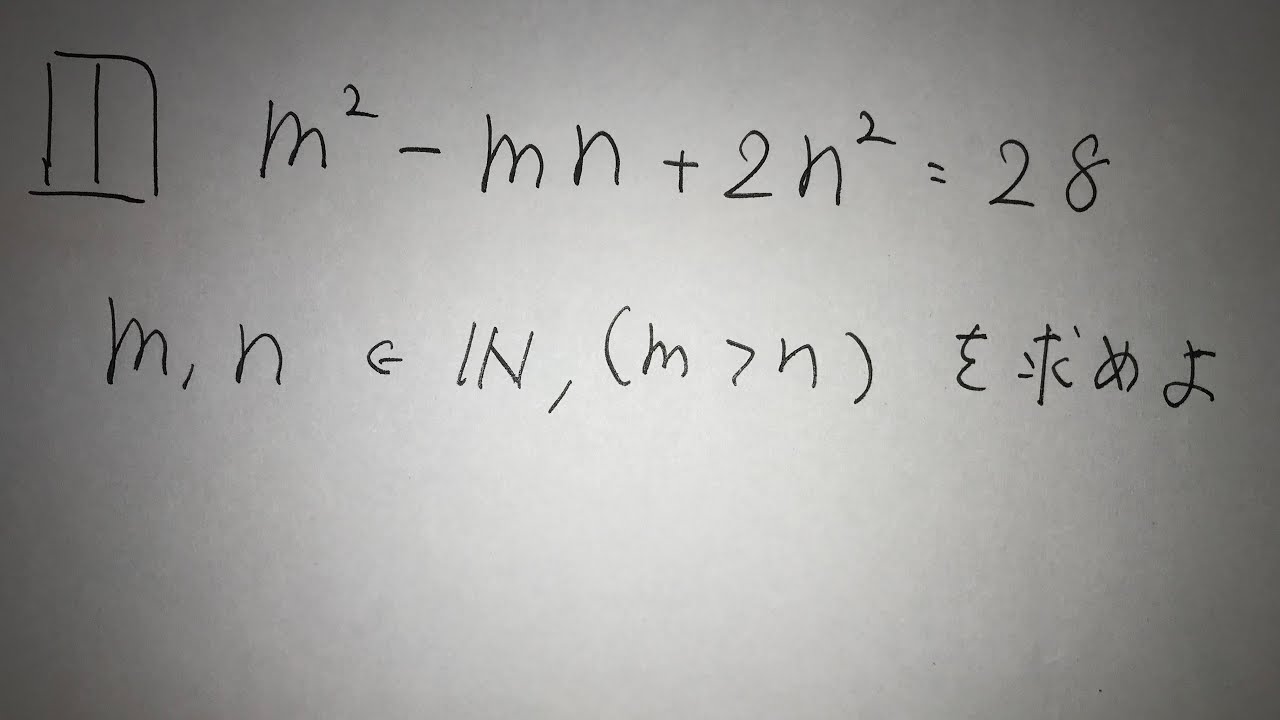
単元:
#数Ⅰ#数A#数Ⅱ#2次関数#式と証明#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
この動画を見る
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k!=m^2$を満たす自然数$(m,n)$をすべて求めよ.
この動画を見る
$\displaystyle \sum_{k=1}^n k!=m^2$を満たす自然数$(m,n)$をすべて求めよ.
ガウス記号

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(6+3\sqrt3)^{2020}]$を$3^{2020}$で割った余りを求めよ.
この動画を見る
$[(6+3\sqrt3)^{2020}]$を$3^{2020}$で割った余りを求めよ.
整数問題
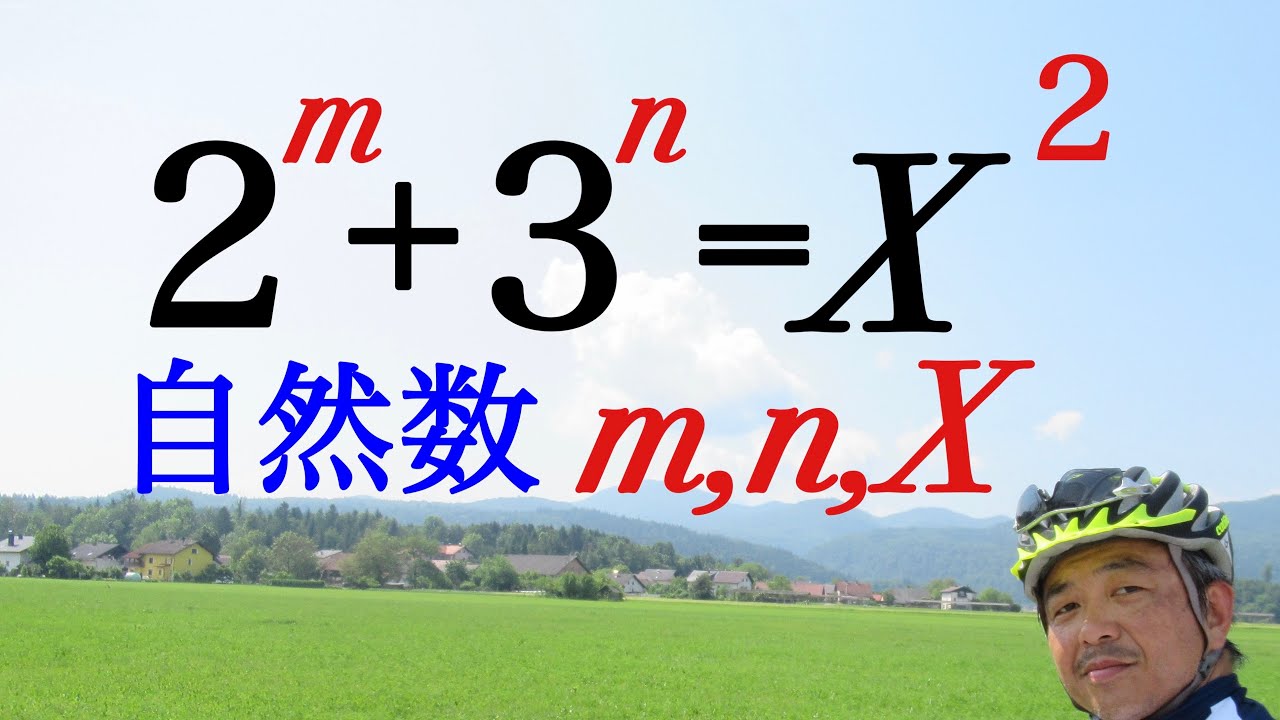
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n,X$は自然数である.これを解け.
$2^m+3^n=X^2$
この動画を見る
$m,n,X$は自然数である.これを解け.
$2^m+3^n=X^2$
整数問題 分数式
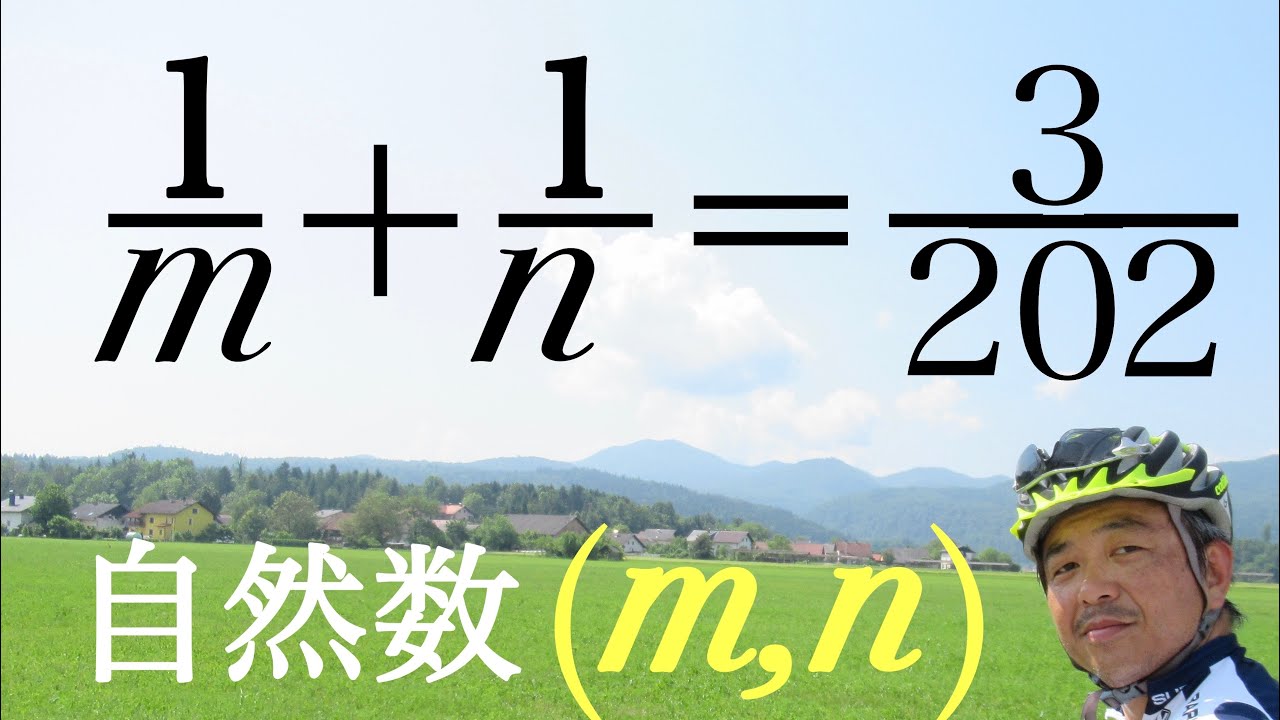
単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は自然数である.
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{202}$
$(m,n)$をすべて求めよ.
この動画を見る
$m,n$は自然数である.
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{202}$
$(m,n)$をすべて求めよ.
整数問題 ピタゴラス数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数である.
$a,b,c$の最大公約数は1であり,$a^2+b^2=c^2$とする.
(1)$a,b$はどちらかは3の倍数であることを示せ.
(2)$a,b$はどちらかは4の倍数であることを示せ.
(3)$a,b,c$のどれかは5の倍数であることを示せ.
この動画を見る
$a,b,c$は自然数である.
$a,b,c$の最大公約数は1であり,$a^2+b^2=c^2$とする.
(1)$a,b$はどちらかは3の倍数であることを示せ.
(2)$a,b$はどちらかは4の倍数であることを示せ.
(3)$a,b,c$のどれかは5の倍数であることを示せ.
息抜き整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の数はすべて整数であるとき,これを解け.
$\sqrt[3]{4913}$
$\sqrt[3]{79507}$
$\sqrt[3]{314432}$
この動画を見る
次の数はすべて整数であるとき,これを解け.
$\sqrt[3]{4913}$
$\sqrt[3]{79507}$
$\sqrt[3]{314432}$
宮崎大 数学的帰納法 合同式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=2^n+1$
$a_n$のうち5で割り切れるものを小さい順に並べた数列を$b_k$とする.
(1)$b_k$を推定せよ.
(2)(1)の推定が全ての自然数$k$で成立することを証明せよ.
宮崎大過去問
この動画を見る
$a_n=2^n+1$
$a_n$のうち5で割り切れるものを小さい順に並べた数列を$b_k$とする.
(1)$b_k$を推定せよ.
(2)(1)の推定が全ての自然数$k$で成立することを証明せよ.
宮崎大過去問
琉球大 剰余 二項定理

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$31^n$を$900$で割った余りが最大になる自然数$n$のうち最小の$n$を求めよ.
1987琉球大過去
この動画を見る
$31^n$を$900$で割った余りが最大になる自然数$n$のうち最小の$n$を求めよ.
1987琉球大過去
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^3+n^2+n+1$が$60$の倍数となる最小の自然数$n$を求めよ.
この動画を見る
$n^3+n^2+n+1$が$60$の倍数となる最小の自然数$n$を求めよ.
N進法 類題 京都大

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
何進法ですか.
$2^{10}=144$
$2^{12}=1104$
京都大過去問
この動画を見る
何進法ですか.
$2^{10}=144$
$2^{12}=1104$
京都大過去問
群馬大(医) ピタゴラス数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数である.
$a^2+b^2=c^2$,$b$が2の累乗が$c$と$b$の差が1である$(a,b,c)$をすべて求めよ.
2018群馬大(医)過去問
この動画を見る
$a,b,c$は自然数である.
$a^2+b^2=c^2$,$b$が2の累乗が$c$と$b$の差が1である$(a,b,c)$をすべて求めよ.
2018群馬大(医)過去問
