数A
数A
答え方が困る？？ 整数問題 （高校数学です）
引けるか！？補助線
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の角度を求めよ（図は動画参照）
$\angle x+\angle y=$
この動画を見る
次の角度を求めよ（図は動画参照）
$\angle x+\angle y=$
福田のおもしろ数学208〜必要条件で絞って十分で切り返す
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
この動画を見る
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
大学入試問題#885「油断したら沼るかも」 #奈良県立医科大学(2014) 三角関数と整数問題
単元：
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典：2014年奈良県立医科大学
この動画を見る
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典：2014年奈良県立医科大学
福田の数学〜千葉大学2024年理系第4問(3)〜コンビネーションに関する不等式の評価
単元：
#数A#大学入試過去問(数学)#場合の数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の整数$n,p,q$が$p > q$かつ$_p\mathrm{C}_2+_q\mathrm{C}_2=n$を満たすとする。$_m\mathrm{C}_2 \leqq n$となる最大の整数$m$を求めよ。
この動画を見る
正の整数$n,p,q$が$p > q$かつ$_p\mathrm{C}_2+_q\mathrm{C}_2=n$を満たすとする。$_m\mathrm{C}_2 \leqq n$となる最大の整数$m$を求めよ。
ピカチュウ割と話せる説
福田のおもしろ数学203〜整数を取る4変数の最大値
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c,d$はすべて正の整数とする。
$a+b+c+d=63$のとき$ab+bc+cd$の最大値を求めよ。
この動画を見る
$a,b,c,d$はすべて正の整数とする。
$a+b+c+d=63$のとき$ab+bc+cd$の最大値を求めよ。
福田の数学〜千葉大学2024年文系第2問〜袋から元に戻さないで球を取り出し得点を考える確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
白球が3個、黒球が5個、赤球が2個入った袋がある。以下のゲームを続けて$n$回続けて行う。
袋から球を1個取り出す。白球だった場合は1点を獲得する。黒球だった場合はさいころを投げて、出た目が3の倍数だった場合には1点、そうでない場合には0点を獲得する。赤球だった場合はコインを投げて、表が出た場合は2点、裏が出た場合は0点を獲得する。取り出した球は袋に戻さない。
(1) $n=2$のとき、総得点がちょうど3点となる確率を求めよ。
(2) $n=3$のとき、総得点がちょうど5点となる確率を求めよ。
(3) $n=3$のとき、総得点が4点以上となる確率を求めよ。
この動画を見る
白球が3個、黒球が5個、赤球が2個入った袋がある。以下のゲームを続けて$n$回続けて行う。
袋から球を1個取り出す。白球だった場合は1点を獲得する。黒球だった場合はさいころを投げて、出た目が3の倍数だった場合には1点、そうでない場合には0点を獲得する。赤球だった場合はコインを投げて、表が出た場合は2点、裏が出た場合は0点を獲得する。取り出した球は袋に戻さない。
(1) $n=2$のとき、総得点がちょうど3点となる確率を求めよ。
(2) $n=3$のとき、総得点がちょうど5点となる確率を求めよ。
(3) $n=3$のとき、総得点が4点以上となる確率を求めよ。
大学入試問題#880「基本の基本！」 #聖マリアンナ医科大学(2021) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#聖マリアンナ医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$n,\sqrt{ n^2+2021 }$がともに自然数のとき、$n$の値をすべて求めよ。
$2021=43\times47$を利用してよい
出典：2021年聖マリアンナ医科大学
この動画を見る
$n,\sqrt{ n^2+2021 }$がともに自然数のとき、$n$の値をすべて求めよ。
$2021=43\times47$を利用してよい
出典：2021年聖マリアンナ医科大学
福田の数学〜千葉大学2024年文系第1問〜三角形の成立条件と対数
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#指数関数と対数関数#対数関数#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(1) 3辺の長さが$2,5,a$である三角形が存在するような、$a$の値の範囲を求めよ。
(2) 3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$である三角形が存在するような、$x$の値の範囲を求めよ。
(3) ある二等辺三角形の3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$であるとき、$x$の値を求めよ。
この動画を見る
(1) 3辺の長さが$2,5,a$である三角形が存在するような、$a$の値の範囲を求めよ。
(2) 3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$である三角形が存在するような、$x$の値の範囲を求めよ。
(3) ある二等辺三角形の3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$であるとき、$x$の値を求めよ。
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
この動画を見る
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
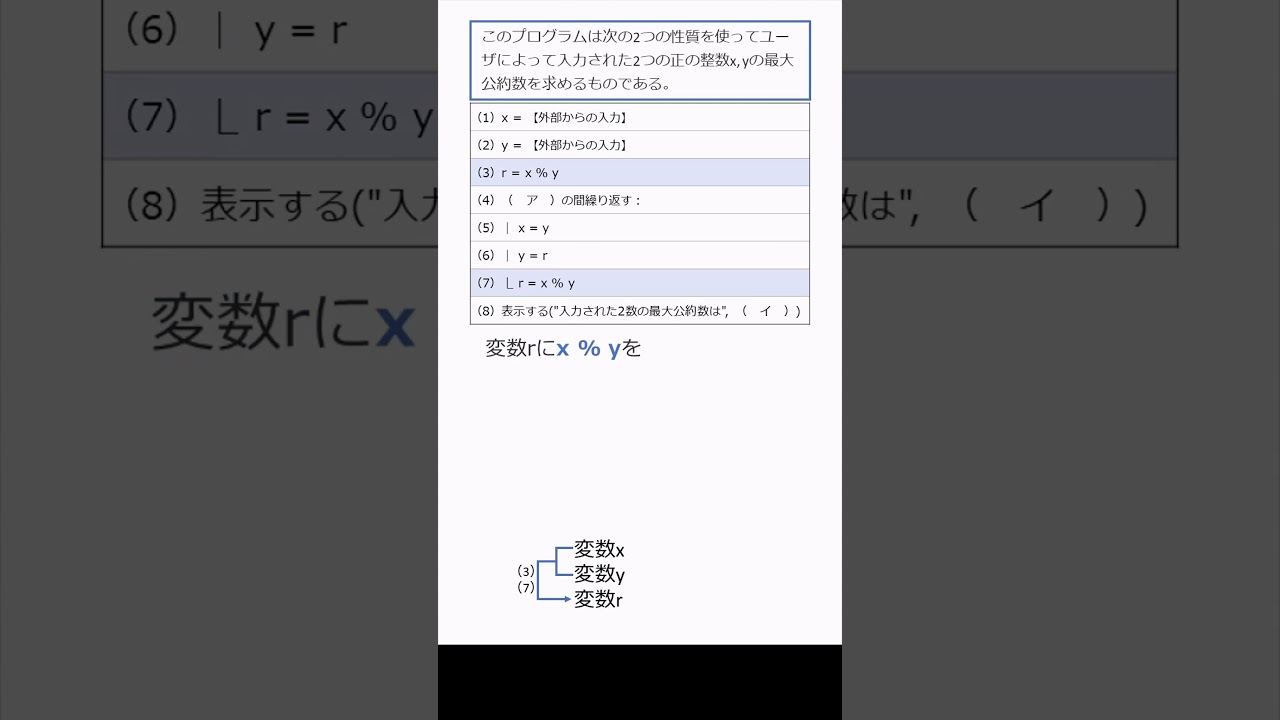
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
この動画を見る
298 ユークリッドの互除法2：余りを計算して効率的に最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の2つの性質を使って最大公約数を求めるものである。
性質1）xをyで割ったあまりが0のとき、xとyの最大公約数はyである。
性質2）xをyで割ったあまりが0と異なるとき、xとyの最大公約数はyとxをyでわったあまりの最大公約数に等しい。
空欄に入る最も適切なものを選べ。
大学入試問題#878「綺麗な問題」 #東北大学医学部AO #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の方程式を満たす整数$x,y$の組$(x,y)$をすべて求めよ。
$x^3+x^2-xy+x+y+4=0$
出典：2019年東北大学医学部AO
この動画を見る
次の方程式を満たす整数$x,y$の組$(x,y)$をすべて求めよ。
$x^3+x^2-xy+x+y+4=0$
出典：2019年東北大学医学部AO
大学入試問題#876「手がかりはどこやろ」 #富山大学(2019) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師：
ますただ
問題文全文(内容文)：
$xyz-3xy-2xz-yz+6x+3y+2z-7=0$を満たす自然数の組$(x,y,z)$をすべて求めよ。
出典：2019年富山大学文系
この動画を見る
$xyz-3xy-2xz-yz+6x+3y+2z-7=0$を満たす自然数の組$(x,y,z)$をすべて求めよ。
出典：2019年富山大学文系
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
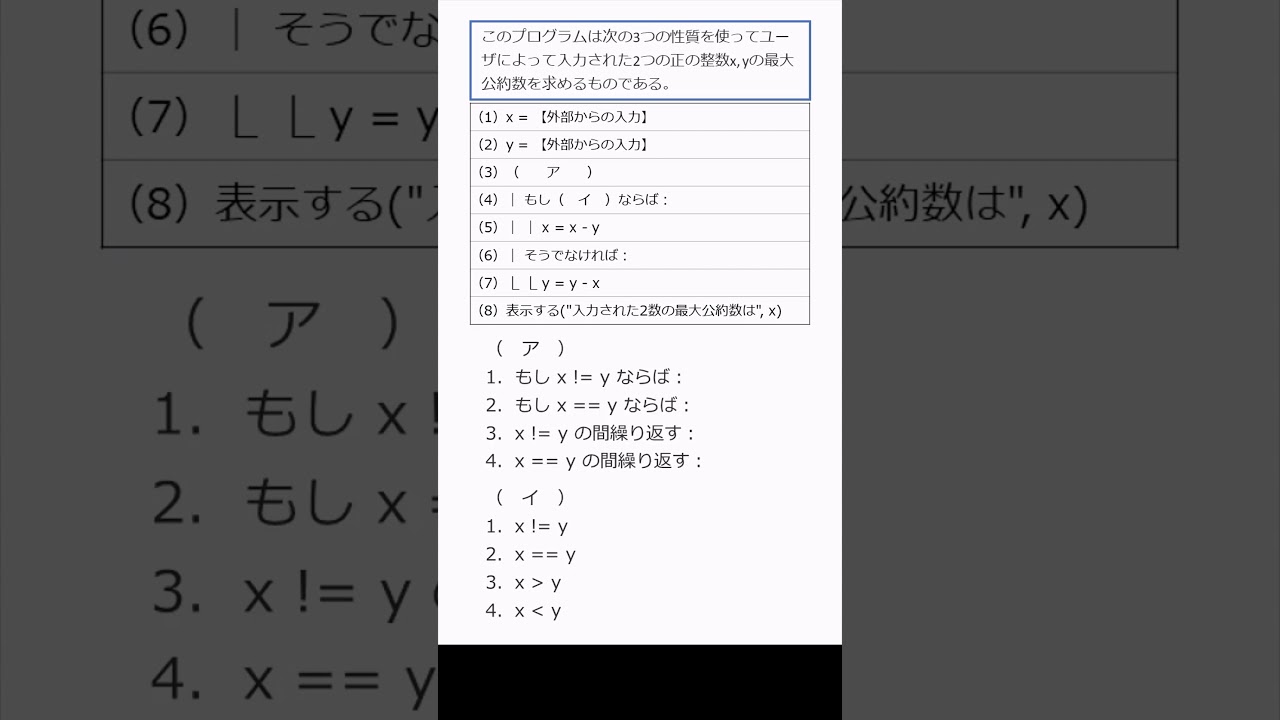
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
この動画を見る
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
※プログラムは動画内参照
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
単元：
#数A#情報Ⅰ(高校生)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師：
めいちゃんねる
問題文全文(内容文)：
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
この動画を見る
297 ユークリッドの互除法1：引き算だけを使って最大公約数を求めよう！ #shorts
【問題文】
このプログラムは次の3つの性質を使って最大公約数を求めるものである。
性質1）xとyの値が等しいとき、xとyの最大公約数はxである。
性質2）xがyより大きいとき、xとyの最大公約数は(x - y)とyの最大公約数に等しい。
性質3）xがyより小さいとき、xとyの最大公約数はxと(y - x)の最大公約数に等しい。
空欄に入る最も適切なものを選べ。
条件付き確率
条件付き確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
本当のことを言う確率が８０％の人が３人いる。
１枚の硬貨を投げたところ、三人とも表が出たと証言した。
本当に表が出た確率を求めよ。
この動画を見る
本当のことを言う確率が８０％の人が３人いる。
１枚の硬貨を投げたところ、三人とも表が出たと証言した。
本当に表が出た確率を求めよ。
福田の数学〜立教大学2024年経済学部第1問(3)〜3回のさいころの目の積が4の倍数となる確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
さいころを $3$ 回投げて出る目をすべてかけた数が $4$ の倍数となる確率は $\fbox{カ}$ である。
この動画を見る
さいころを $3$ 回投げて出る目をすべてかけた数が $4$ の倍数となる確率は $\fbox{カ}$ である。
【保存版】相加平均・相乗平均の覚え方
単元：
#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#その他#数学(高校生)#参考書紹介
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
【保存版】相加平均・相乗平均の覚え方
※問題は動画内参照
この動画を見る
【保存版】相加平均・相乗平均の覚え方
※問題は動画内参照
三角形の重心 一点で交わるのはなぜ？
内心 内角の二等分線が一点で交わるのはなぜ？
福田の数学〜立教大学2024年理学部第2問〜反復試行の確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1$ から $6$ の番号がひとつずつ重複なくつけられた $6$ つの箱がある。このとき、次の試行を行う。
$\fbox{さいころを $1$ つ投げて、出た目の番号のついた箱に玉を $1$ つ入れる。}$
この試行を繰り返し、いずれかの箱に玉が $3$ 個入った時点で終了する。ただし、$1$ 回目の試行を行う前は、どの箱にも玉は $1$ 個も入っていないとする。終了するまでに行った試行の回数を $N$ とする。
$(1)$ $N$ のとりうる最小値 $N_0$ と最大値 $N_1$ をそれぞれ求めよ。
$(2)$ $N=N_{0}$ となる確率を求めよ。
$(3)$ $N=N_{0}+1$ となる確率を求めよ。
$(4)$ 試行を $6$ 回行った時点で、すべての箱に $1$ つずつ玉が入るという事象を $A$ とする。また、$N=N_{1}$ となる事象を $B$ とする。事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ を求めよ。
$(5)$ $N=N_{1}$ となる確率を $P$ とするとき、$6^{8}P$ は整数となる。その値を求めよ。
この動画を見る
$1$ から $6$ の番号がひとつずつ重複なくつけられた $6$ つの箱がある。このとき、次の試行を行う。
$\fbox{さいころを $1$ つ投げて、出た目の番号のついた箱に玉を $1$ つ入れる。}$
この試行を繰り返し、いずれかの箱に玉が $3$ 個入った時点で終了する。ただし、$1$ 回目の試行を行う前は、どの箱にも玉は $1$ 個も入っていないとする。終了するまでに行った試行の回数を $N$ とする。
$(1)$ $N$ のとりうる最小値 $N_0$ と最大値 $N_1$ をそれぞれ求めよ。
$(2)$ $N=N_{0}$ となる確率を求めよ。
$(3)$ $N=N_{0}+1$ となる確率を求めよ。
$(4)$ 試行を $6$ 回行った時点で、すべての箱に $1$ つずつ玉が入るという事象を $A$ とする。また、$N=N_{1}$ となる事象を $B$ とする。事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ を求めよ。
$(5)$ $N=N_{1}$ となる確率を $P$ とするとき、$6^{8}P$ は整数となる。その値を求めよ。
『3×4=?』
これなんで？ フルは↑
単元：
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
これなんで？ フルは↑
【問題文】20×20
この動画を見る
これなんで？ フルは↑
【問題文】20×20
福田の数学〜立教大学2024年理学部第1問(2)〜17のn乗の1の位
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
「20+20=200」になる理由を解説
単元：
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
「20+20=200」になる理由を解説しています。
この動画を見る
「20+20=200」になる理由を解説しています。
【高校数学】円と直線が接するときの２パターンの考え方【数学のコツ】
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の円と直線が接するときの$k$の値と接点の座標を求めよ。
$x^2+y^2=4, y=x+k$
この動画を見る
次の円と直線が接するときの$k$の値と接点の座標を求めよ。
$x^2+y^2=4, y=x+k$
赤玉、白玉 の確率 初心者はここで間違える
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
赤玉5個、白玉7個の入った袋から、4個の玉を同時に取り出すとき、その中に赤玉が3個以上含まれる確率を求めよ。
この動画を見る
赤玉5個、白玉7個の入った袋から、4個の玉を同時に取り出すとき、その中に赤玉が3個以上含まれる確率を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第5問〜ある対数とそれを超えない最大の整数
単元：
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$－$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$－$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$－1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$－1 となるために$x$が満たすべき必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$－$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$－$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$－1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$－1 となるために$x$が満たすべき必要十分条件を求めよ。