数A
数A
福田の数学〜慶應義塾大学薬学部2025第1問(2)〜正八面体に内接する立方体の体積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#立体図形#立体切断#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学457〜不定方程式の解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 = 2(y+z) \\
x^6 = y^6 +z^6 + 31 (y^2+z^2)
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数$x,y,z$を求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 = 2(y+z) \\
x^6 = y^6 +z^6 + 31 (y^2+z^2)
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数$x,y,z$を求めて下さい。
約分のこの技知ってた？
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\frac{1817}{2923}$を約分しなさい。
この動画を見る
$\frac{1817}{2923}$を約分しなさい。
福田の数学〜東北大学2025理系第1問〜反復試行の確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
原点を出発点として数直線上を動く点$P$がある。
試行(＊)を次のように定める。
(＊)
$1$枚の硬貨を$1$回投げて、
・表が出た場合は点$P$を正の向きに$1$だけ進める。
・裏が出た場合は$1$個のさいころを$1$回投げ、
奇数の目が出た場合は点$P$を正の向きに$1$だけ進める
偶数の目が出た場合は点$P$を負の向きに$2$だけ進める
ただし、硬貨を投げたとき裏表の出る確率は
それぞれ$\dfrac{1}{2}$,さいころを投げたとき
$1$から$6$までの整数の目の出る確率は
それぞれ$\dfrac{1}{6}$とする。
(1)試行(＊)を$3$回繰り返した後に、
点$P$が原点に戻っている確率を求めよ。
(2)試行(＊)を$6$回繰り返した後に、
点$P$が原点に戻っている確率を求めよ。
(3)$n$を$3$で割り切れない正の整数とする。
試行(＊)を$n$回繰り返した後に、
点$P$が原点に戻っている確率を求めよ。
$2025$年東北大学理系過去問題
この動画を見る
$\boxed{1}$
原点を出発点として数直線上を動く点$P$がある。
試行(＊)を次のように定める。
(＊)
$1$枚の硬貨を$1$回投げて、
・表が出た場合は点$P$を正の向きに$1$だけ進める。
・裏が出た場合は$1$個のさいころを$1$回投げ、
奇数の目が出た場合は点$P$を正の向きに$1$だけ進める
偶数の目が出た場合は点$P$を負の向きに$2$だけ進める
ただし、硬貨を投げたとき裏表の出る確率は
それぞれ$\dfrac{1}{2}$,さいころを投げたとき
$1$から$6$までの整数の目の出る確率は
それぞれ$\dfrac{1}{6}$とする。
(1)試行(＊)を$3$回繰り返した後に、
点$P$が原点に戻っている確率を求めよ。
(2)試行(＊)を$6$回繰り返した後に、
点$P$が原点に戻っている確率を求めよ。
(3)$n$を$3$で割り切れない正の整数とする。
試行(＊)を$n$回繰り返した後に、
点$P$が原点に戻っている確率を求めよ。
$2025$年東北大学理系過去問題
福田のおもしろ数学448〜2変数の方程式の実数解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{x+6}{y}+\dfrac{13}{xy}=\dfrac{4-y}{x}$
を満たす実数の組$(x,y)$を求めよ。
この動画を見る
$\dfrac{x+6}{y}+\dfrac{13}{xy}=\dfrac{4-y}{x}$
を満たす実数の組$(x,y)$を求めよ。
福田の数学〜北海道大学2025理系第5問〜条件を満たす3つの整数を選び出す場合の数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$n$を$3$以上の整数とする。
(1)$k$を整数とする。
$k\lt a\lt b \lt c \leqq k+n$を満たす
整数$a,b,c$の選び方の
総数を$n$の式で表せ。
(2)$1\leqq a \lt b \lt c \leqq 2n$を満たす
整数$a,b,c$のうち、
$a+b \gt c$となる$a,b,c$の選び方の総数を$L$とする。
このとき、$L\gt {}_n \mathrm{ C }_3 $であることを示せ。
この動画を見る
$\boxed{5}$
$n$を$3$以上の整数とする。
(1)$k$を整数とする。
$k\lt a\lt b \lt c \leqq k+n$を満たす
整数$a,b,c$の選び方の
総数を$n$の式で表せ。
(2)$1\leqq a \lt b \lt c \leqq 2n$を満たす
整数$a,b,c$のうち、
$a+b \gt c$となる$a,b,c$の選び方の総数を$L$とする。
このとき、$L\gt {}_n \mathrm{ C }_3 $であることを示せ。
福田の数学〜北海道大学2025理系第2問〜円に引いた2本の接線でできる四角形の面積の最大最小
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
円$C_1:x^2+y^2=1$を考える。
実数$p,q$が$p^2+q^2 \gt 1$を満たすとき、
点$p(p,q)$から$C_1$に引いた$2$本の接線$\ell_1,\ell_2$の
接点をそれぞれ$Q_1(x_1,y_1), Q_2(x_2,y_2)$とする。
また、座標平面上の原点を$O(0,0)$とする。
(1)直線$\ell_1,\ell_2$,線分$OQ_1,OQ_2$で囲まれた
四角形の面積$S$を$p,q$を用いて表せ。
(2)点$P$が楕円
$C_2:\dfrac{x^2}{2}+\dfrac{y^2}{3}=1$
の上を動くとき、
(1)の四角形の面積$S$の最大値と最小値を求めよ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{2}$
円$C_1:x^2+y^2=1$を考える。
実数$p,q$が$p^2+q^2 \gt 1$を満たすとき、
点$p(p,q)$から$C_1$に引いた$2$本の接線$\ell_1,\ell_2$の
接点をそれぞれ$Q_1(x_1,y_1), Q_2(x_2,y_2)$とする。
また、座標平面上の原点を$O(0,0)$とする。
(1)直線$\ell_1,\ell_2$,線分$OQ_1,OQ_2$で囲まれた
四角形の面積$S$を$p,q$を用いて表せ。
(2)点$P$が楕円
$C_2:\dfrac{x^2}{2}+\dfrac{y^2}{3}=1$
の上を動くとき、
(1)の四角形の面積$S$の最大値と最小値を求めよ。
$2025$年北海道大学理系過去問題
福田のおもしろ数学444〜難しい対数方程式の解
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt x=\log_2 x$
を満たす実数$x$をすべて求めてください。
この動画を見る
$\sqrt x=\log_2 x$
を満たす実数$x$をすべて求めてください。
福田のおもしろ数学442〜nが[√n]で割り切れるようなn
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
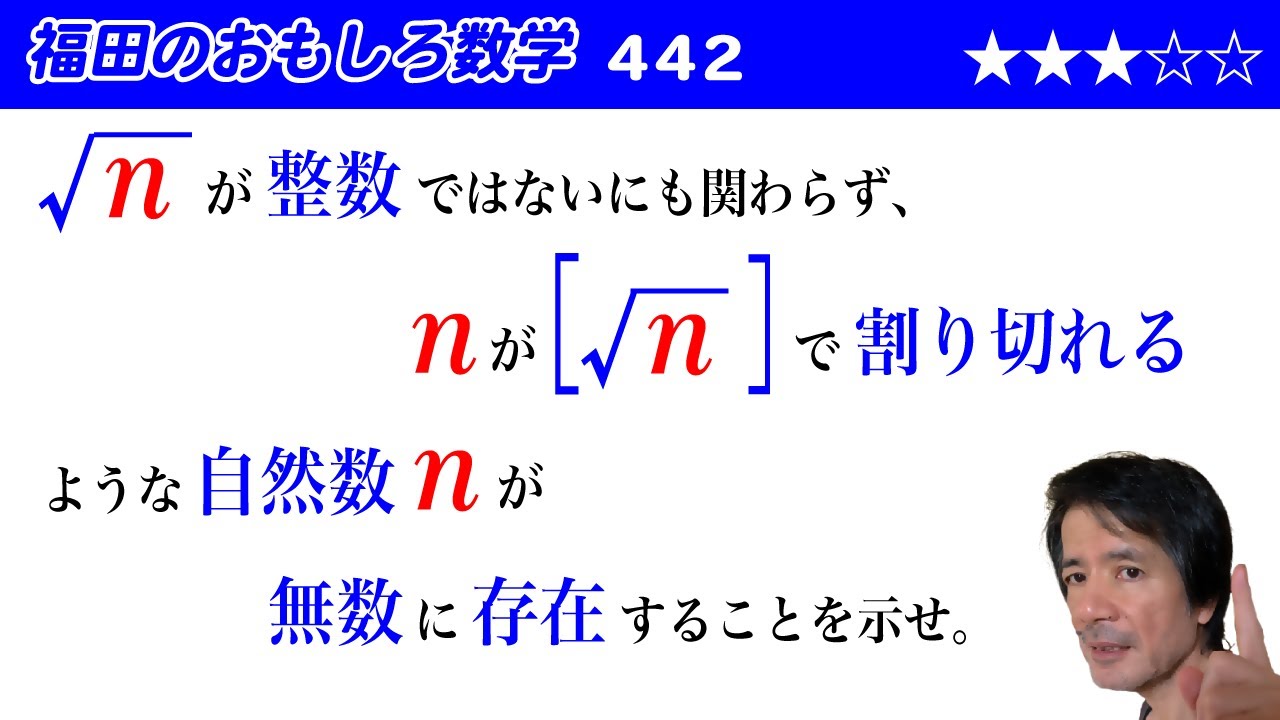
$\sqrt n$が整数ではないにも関わらず、
$n$が$\left[\sqrt n\right]$で割り切れるような自然数$n$が
無限に存在することを示せ。
この動画を見る
$\sqrt n$が整数ではないにも関わらず、
$n$が$\left[\sqrt n\right]$で割り切れるような自然数$n$が
無限に存在することを示せ。
福田のおもしろ数学440〜正五角形10個でできる図形の内接円と外接円の面積の関係
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
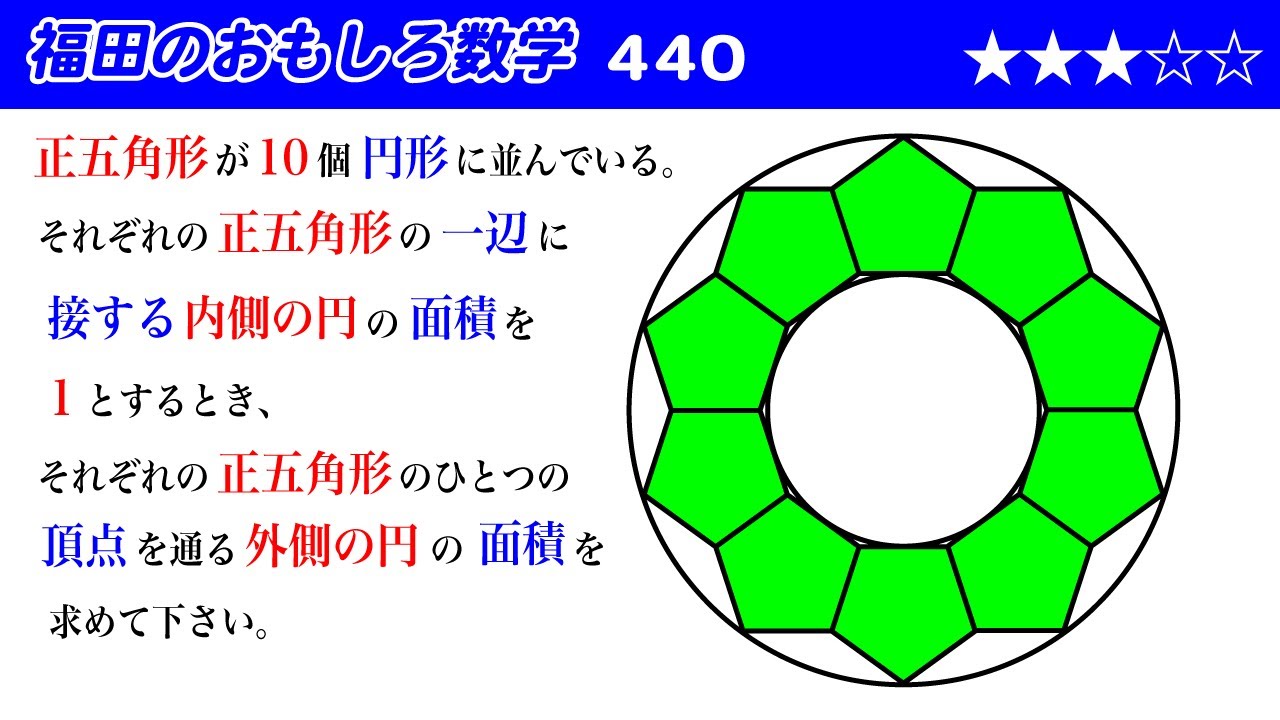
正五角形が$10$個円形に並んでいる。
それぞれの正五角形に一辺に
接する内側の円の面積を$1$とするとき、
それぞれの正五角形のひとつの
頂点を通る外側の円の面積を求めて下さい。
図は動画内参照
この動画を見る
正五角形が$10$個円形に並んでいる。
それぞれの正五角形に一辺に
接する内側の円の面積を$1$とするとき、
それぞれの正五角形のひとつの
頂点を通る外側の円の面積を求めて下さい。
図は動画内参照
福田の数学〜京都大学2025文系第1問(2)〜整数の割り算で割り切れる条件
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$n^4+6n^2+23$が$n^2+n+3$で
割り切れるような正の整数$n$をすべて求めよ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{1}$
(2)$n^4+6n^2+23$が$n^2+n+3$で
割り切れるような正の整数$n$をすべて求めよ。
$2025$年京都大学文系過去問題
福田のおもしろ数学435〜正三角形の内部の点の位置から面積を求める
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
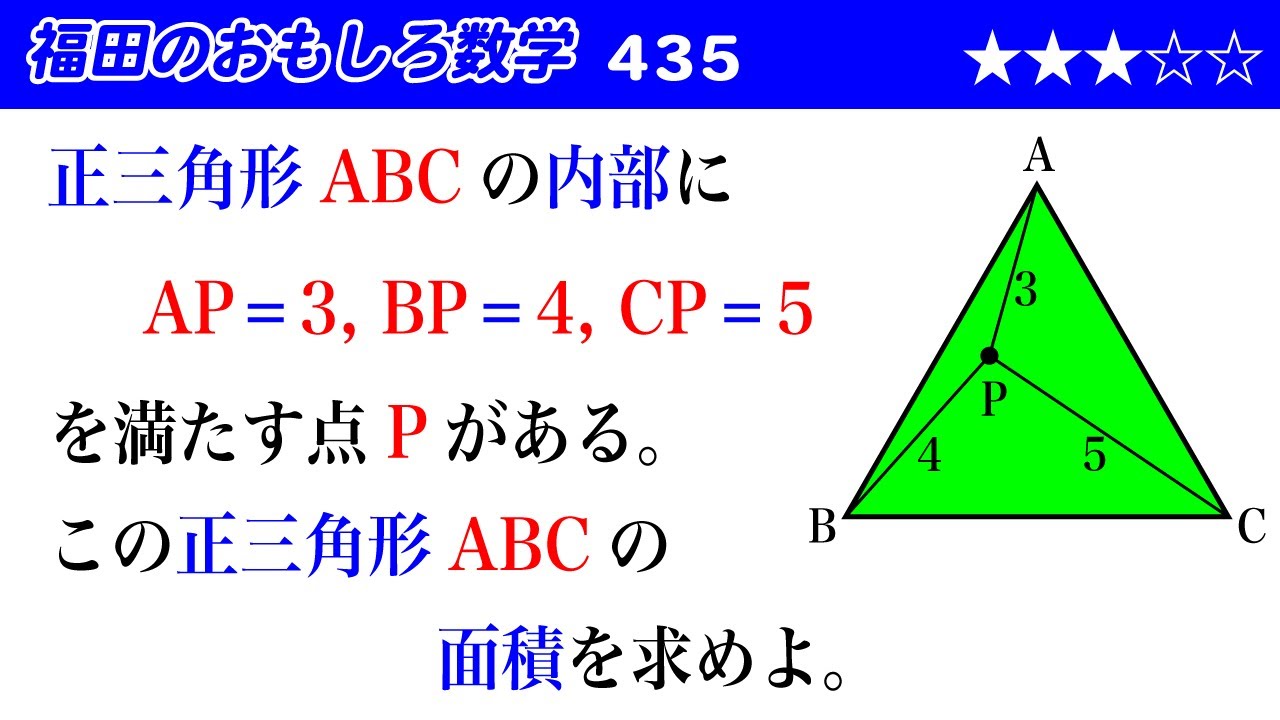
正三角形$ABC$の内部に
$AP=3,BP=4,CP=5$を満たす点$P$がある。
この正三角形$ABC$の面積を求めよ。
図は動画内参照
この動画を見る
正三角形$ABC$の内部に
$AP=3,BP=4,CP=5$を満たす点$P$がある。
この正三角形$ABC$の面積を求めよ。
図は動画内参照
福田のおもしろ数学433〜四面体に関する計量問題
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
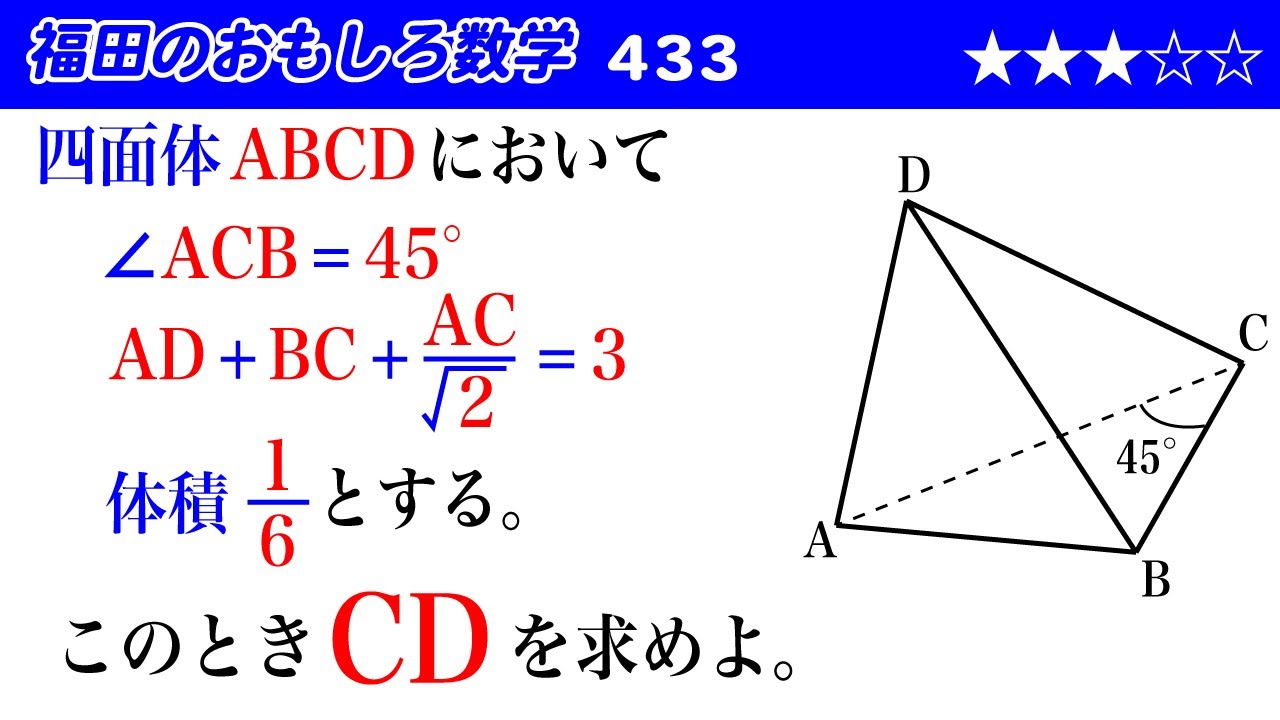
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
この動画を見る
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
福田の数学〜京都大学2025理系第2問〜不定方程式で表された数の最小値
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
【数A】【場合の数と確率】期待値、このゲームは得？損？ ※問題文は概要欄
単元：
#数A#場合の数と確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
白玉2個、黒玉5個、赤玉3個が入っている袋から玉を1個取り出し、白玉が出たら1000円、黒玉が出たら100円もらえ、赤玉が出たら800円を支払うゲームがある。ゲームの参加料が0円であるとき、このゲームに参加することは得であるといえるか。
この動画を見る
白玉2個、黒玉5個、赤玉3個が入っている袋から玉を1個取り出し、白玉が出たら1000円、黒玉が出たら100円もらえ、赤玉が出たら800円を支払うゲームがある。ゲームの参加料が0円であるとき、このゲームに参加することは得であるといえるか。
【数A】【場合の数と確率】コインを投げたときの得点の期待値 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
3枚の硬貨を同時に投げて、表が3枚出たら100点、2枚出たら50点を獲得し、1枚のときは60点を、1枚も出ていないときは70点を失うものとする。1回硬貨を投げるときの得点の期待値を求めよ。
この動画を見る
3枚の硬貨を同時に投げて、表が3枚出たら100点、2枚出たら50点を獲得し、1枚のときは60点を、1枚も出ていないときは70点を失うものとする。1回硬貨を投げるときの得点の期待値を求めよ。
【数A】【場合の数と確率】さいころ2個の目の積の期待値 ※問題文は概要欄
【数A】【場合の数と確率】条件付き確率、帽子を忘れてくる確率 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
5回に1回の割合で帽子を忘れるくせのあるK君が、正月A、B、C3軒を順に年始回りをして家に帰ったところ、帽子を忘れてきたことに気がついた。2番目の家Bに忘れてきた確率を求めよ。
この動画を見る
5回に1回の割合で帽子を忘れるくせのあるK君が、正月A、B、C3軒を順に年始回りをして家に帰ったところ、帽子を忘れてきたことに気がついた。2番目の家Bに忘れてきた確率を求めよ。
【数A】【場合の数と確率】条件付き確率、原因の確率 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
ある電器店が、A社、B社、C社から同じ製品を仕入れた。A社、B社、C社から仕入れた比率は4:3:2であり、製品が不良品である比率はそれぞれ3%、4%、5%であるという。いま、大量にある3社の製品をよく混ぜ、その中から1個抜き取って調べたところ、不良品であった。これがA社から仕入れたものである確率を求めよ。
この動画を見る
ある電器店が、A社、B社、C社から同じ製品を仕入れた。A社、B社、C社から仕入れた比率は4:3:2であり、製品が不良品である比率はそれぞれ3%、4%、5%であるという。いま、大量にある3社の製品をよく混ぜ、その中から1個抜き取って調べたところ、不良品であった。これがA社から仕入れたものである確率を求めよ。
【数A】【場合の数と確率】条件付き確率2 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
Aの袋には白玉3個と赤玉2個、Bの袋には白玉2個と赤玉3個、Cの袋には白玉1個と赤玉4個が入っている。1個のさいころを投げて1の目が出たらAの袋を、2,3の目が出たらBの袋を、4～6の目が出たらCの袋を選び、1個の玉を取り出すものとする。取り出された玉が白玉であったとき、それがCの袋から取り出された玉である確率を求めよ。
この動画を見る
Aの袋には白玉3個と赤玉2個、Bの袋には白玉2個と赤玉3個、Cの袋には白玉1個と赤玉4個が入っている。1個のさいころを投げて1の目が出たらAの袋を、2,3の目が出たらBの袋を、4～6の目が出たらCの袋を選び、1個の玉を取り出すものとする。取り出された玉が白玉であったとき、それがCの袋から取り出された玉である確率を求めよ。
【数A】【場合の数と確率】条件付き確率1 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
ジョーカーを除く1組52枚のトランプから2枚のカードを同時に抜き出す。2枚のうちの少なくとも1枚はハートであることがわかっているとき、残りの1枚もハートである確率を求めよ。
この動画を見る
ジョーカーを除く1組52枚のトランプから2枚のカードを同時に抜き出す。2枚のうちの少なくとも1枚はハートであることがわかっているとき、残りの1枚もハートである確率を求めよ。
【数A】【場合の数と確率】確率の乗法定理 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
箱Aには赤玉3個と白玉2個、箱Bには赤玉と白玉2個ずつ入っている。
(1)箱Aから玉を1個取り出し、それを箱Bに入れた後、箱Bから玉を1個取り出すとき、それが赤玉である確率を求めよ。
(2)箱Aから玉を2個取り出し、それを箱Bに入れた後、箱Bから玉を2個同時に取り出すとき、それらが2個とも赤玉である確率を求めよ。
この動画を見る
箱Aには赤玉3個と白玉2個、箱Bには赤玉と白玉2個ずつ入っている。
(1)箱Aから玉を1個取り出し、それを箱Bに入れた後、箱Bから玉を1個取り出すとき、それが赤玉である確率を求めよ。
(2)箱Aから玉を2個取り出し、それを箱Bに入れた後、箱Bから玉を2個同時に取り出すとき、それらが2個とも赤玉である確率を求めよ。
【数A】【場合の数と確率】確率の条件から未知数の決定 ※問題文は概要欄
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
1つのつぼに赤玉と白玉が合計10個入っている。このつぼから1個の玉を取り出し、それをつぼに戻さずにまた1個の玉を取り出す。このとき、取り出される2個の玉がともに赤玉である確率は7/15であるという。このつぼに初め赤玉は何個入っているか。
この動画を見る
1つのつぼに赤玉と白玉が合計10個入っている。このつぼから1個の玉を取り出し、それをつぼに戻さずにまた1個の玉を取り出す。このとき、取り出される2個の玉がともに赤玉である確率は7/15であるという。このつぼに初め赤玉は何個入っているか。
福田の数学〜東京大学2025文系第3問〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
白玉$2$個が横に並んでいる。
投げたとき表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインを用いて、
次の手順 (＊) をくり返し、
白玉または黒玉を横一列に並べていく。
手順(＊)
$\quad$コインを投げ、
$\quad$表が出たら白玉、裏が出たら黒玉を、
$\quad$それまでに並べられている一番右にある玉の
$\quad$右隣におく。
$\quad$そして、新しくおいた玉の色が
$\quad$その$1$つ左の玉の色と異なり、
$\quad$かつ$2$つ左の玉の色と一致するときには、
$\quad$新しくおいた玉の$1$つ左の玉を新しくおいた玉と
$\quad$同じ色の玉にとりかえる。
例えば、手順(＊)を$2$回行いコインが裏、表の順に
出た場合には、白玉が$4$つ並ぶ。
正の整数$n$に対して、手順(＊)を$n$回行った時点での
$(n + 2)$個の玉の並び方を考える。
(1)$n = 3$のとき、
右から$2$番目の玉が白玉である確率を求めよ。
(2)$n$を正の整数とする。
右から$2$番目の玉が白玉である確率を求めよ。
(3)$n$を正の整数とする。
右から$1$番目と$2$番目の玉がともに白玉である確率を求めよ。
$2025$年東京大学文系過去問題
この動画を見る
$\boxed{3}$
白玉$2$個が横に並んでいる。
投げたとき表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインを用いて、
次の手順 (＊) をくり返し、
白玉または黒玉を横一列に並べていく。
手順(＊)
$\quad$コインを投げ、
$\quad$表が出たら白玉、裏が出たら黒玉を、
$\quad$それまでに並べられている一番右にある玉の
$\quad$右隣におく。
$\quad$そして、新しくおいた玉の色が
$\quad$その$1$つ左の玉の色と異なり、
$\quad$かつ$2$つ左の玉の色と一致するときには、
$\quad$新しくおいた玉の$1$つ左の玉を新しくおいた玉と
$\quad$同じ色の玉にとりかえる。
例えば、手順(＊)を$2$回行いコインが裏、表の順に
出た場合には、白玉が$4$つ並ぶ。
正の整数$n$に対して、手順(＊)を$n$回行った時点での
$(n + 2)$個の玉の並び方を考える。
(1)$n = 3$のとき、
右から$2$番目の玉が白玉である確率を求めよ。
(2)$n$を正の整数とする。
右から$2$番目の玉が白玉である確率を求めよ。
(3)$n$を正の整数とする。
右から$1$番目と$2$番目の玉がともに白玉である確率を求めよ。
$2025$年東京大学文系過去問題
【数A】【図形の性質】空間図形の応用3 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
立方体の各面の対角線の交点を頂点とし、
隣り合った面どうしの頂点を結ぶことによって、
立方体の中に正八面体ができる。
このとき、次の場合について、
正八面体の体積を求めよ。
(1) 立方体の1辺の長さが 10
(2) 正八面体の1辺の長さが6
一辺の長さが５の正八角形について、
次のものを求めよ。
(1) 正八角形の体積V
(2) 正八角形に内接する球の半径ｒ
この動画を見る
立方体の各面の対角線の交点を頂点とし、
隣り合った面どうしの頂点を結ぶことによって、
立方体の中に正八面体ができる。
このとき、次の場合について、
正八面体の体積を求めよ。
(1) 立方体の1辺の長さが 10
(2) 正八面体の1辺の長さが6
一辺の長さが５の正八角形について、
次のものを求めよ。
(1) 正八角形の体積V
(2) 正八角形に内接する球の半径ｒ
【数A】【図形の性質】空間図形の応用2 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
四面体ABCD において，辺AB と辺CDが垂直ならば，頂点Aから平面BCDに下ろした垂線AHと，頂点Bから平面CDAに下ろした垂線BKは交わることを示せ。ただし，HとB，KとAはそれぞれ一致しないものとする。
直方体 ABCD-EFGHにおいて，
辺AB，AD，AEの長さをそれぞれa，b，cとする。
また，頂点Aから直線FHに下ろした垂線をAK とする。
このとき，次の問いに答えよ。
(1) EK⊥FHであることを証明せよ。
(2) 垂線AKの長さを求めよ。
この動画を見る
四面体ABCD において，辺AB と辺CDが垂直ならば，頂点Aから平面BCDに下ろした垂線AHと，頂点Bから平面CDAに下ろした垂線BKは交わることを示せ。ただし，HとB，KとAはそれぞれ一致しないものとする。
直方体 ABCD-EFGHにおいて，
辺AB，AD，AEの長さをそれぞれa，b，cとする。
また，頂点Aから直線FHに下ろした垂線をAK とする。
このとき，次の問いに答えよ。
(1) EK⊥FHであることを証明せよ。
(2) 垂線AKの長さを求めよ。
【数A】【図形の性質】空間図形の応用1 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
空間内の異なる2つの直線ℓ 、m と異なる2つの平面α,βについて，
次の記述は常に正しいか。
(1) ℓ⊥α、ｍ⊥αならば、ℓ⊥ｍである。
(2) ℓ⊥α、ｍ⊥αならば、α//βである。
(3) ℓ//α、ｍ//αならば、ℓ//ｍである。
(4) ℓ//α、ｍ⊥αならば、ℓと並行でｍと垂直な直線がある。
正六角柱を底面に
平行でない1つの平面で切ったものである。
六角形ABCDEF について，
辺AB と平行な辺を答えよ。
立方体について、次の問いに答えよ。
(1) 辺BF と垂直な面をすべて答えよ。
(2) 平面 BFHD と平行な辺をすべて答えよ。
(3) この立方体に，平行な位置関係にある面は何組あるか。
(4) 平面ABGHと垂直な面をすべて答えよ。
この動画を見る
空間内の異なる2つの直線ℓ 、m と異なる2つの平面α,βについて，
次の記述は常に正しいか。
(1) ℓ⊥α、ｍ⊥αならば、ℓ⊥ｍである。
(2) ℓ⊥α、ｍ⊥αならば、α//βである。
(3) ℓ//α、ｍ//αならば、ℓ//ｍである。
(4) ℓ//α、ｍ⊥αならば、ℓと並行でｍと垂直な直線がある。
正六角柱を底面に
平行でない1つの平面で切ったものである。
六角形ABCDEF について，
辺AB と平行な辺を答えよ。
立方体について、次の問いに答えよ。
(1) 辺BF と垂直な面をすべて答えよ。
(2) 平面 BFHD と平行な辺をすべて答えよ。
(3) この立方体に，平行な位置関係にある面は何組あるか。
(4) 平面ABGHと垂直な面をすべて答えよ。
【数A】【図形の性質】作図の応用 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
線分ABが与えられたとき, 線分ABを斜辺とし, ∠BAC=60° である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
この動画を見る
線分ABが与えられたとき, 線分ABを斜辺とし, ∠BAC=60° である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
【数A】【図形の性質】円の位置関係 ※問題文は概要欄
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図のように，数直線上の原点を中心とする半径3の円Oと、
この数直線上を動く点Pを中心とする半径2の円Pがある。
Pの座標をtとするとき,次の件を満たすとの値,またはtの値の範囲を求めよ。
(1) 2円O，Pの共通接線が4本引ける。
(2) 2円O，Pの共有点が1個である。
(3) 2円O，Pの共通接線が、座標が6である数直線上の点Aを通る。
図のように，半径3の外接する2円A, B
が、半径8の円Oに内接している。2円A, B
に外接し，円Oに内接する円Cの半径を求めよ。
この動画を見る
図のように，数直線上の原点を中心とする半径3の円Oと、
この数直線上を動く点Pを中心とする半径2の円Pがある。
Pの座標をtとするとき,次の件を満たすとの値,またはtの値の範囲を求めよ。
(1) 2円O，Pの共通接線が4本引ける。
(2) 2円O，Pの共有点が1個である。
(3) 2円O，Pの共通接線が、座標が6である数直線上の点Aを通る。
図のように，半径3の外接する2円A, B
が、半径8の円Oに内接している。2円A, B
に外接し，円Oに内接する円Cの半径を求めよ。
福田のおもしろ数学424〜直角二等辺三角形の斜辺を1：2：√3に内分する点がAと作る角が45°になる証明
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
直角二等辺三角形$ABC$で
斜辺$BC$を$1:2:\sqrt3$に
分ける点を順に$D,E$とする。
$\angle DAE=45°$
であることを証明せよ。
図は動画内参照
この動画を見る
直角二等辺三角形$ABC$で
斜辺$BC$を$1:2:\sqrt3$に
分ける点を順に$D,E$とする。
$\angle DAE=45°$
であることを証明せよ。
図は動画内参照