 数A
数A
 数A
数A
キレイに解けます 立命館高校
単元:
#数学(中学生)#中2数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
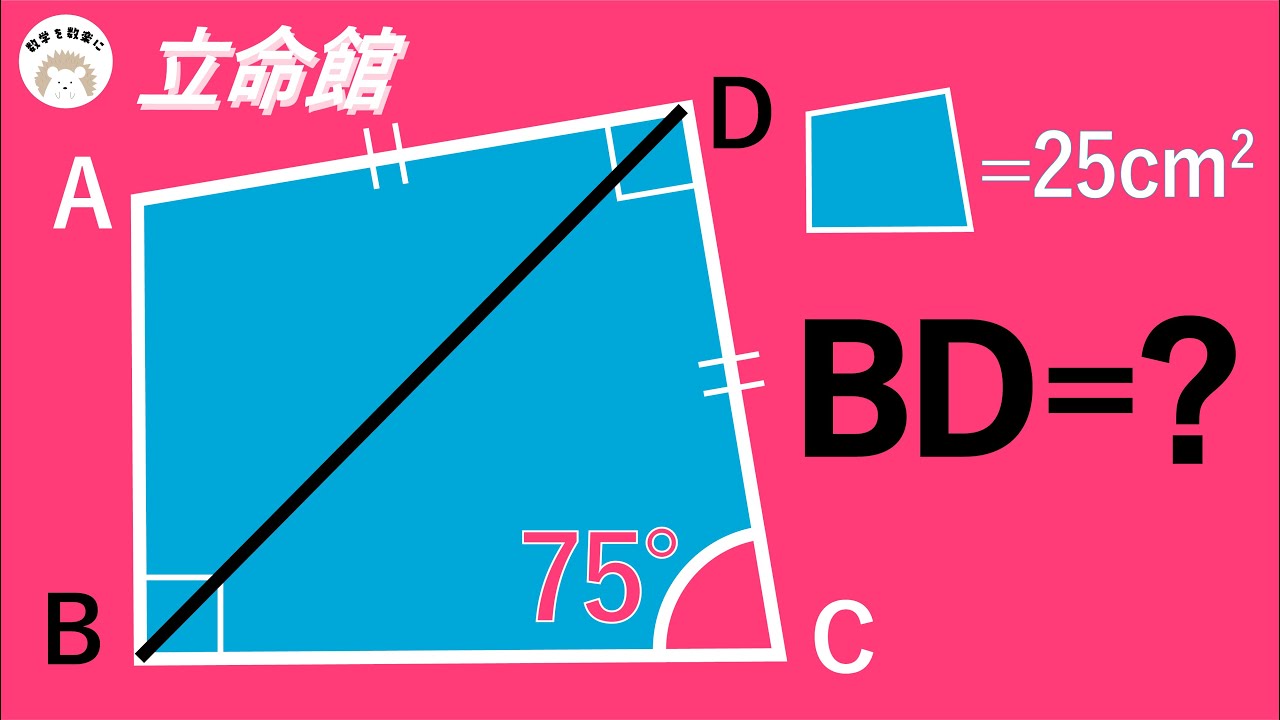
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
この動画を見る
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
Rony先生の問題はやっぱり面白い!!3通りで解説!!
11三重県教員採用試験(数学:1番 整数問題)

単元:
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
この動画を見る
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
整数問題
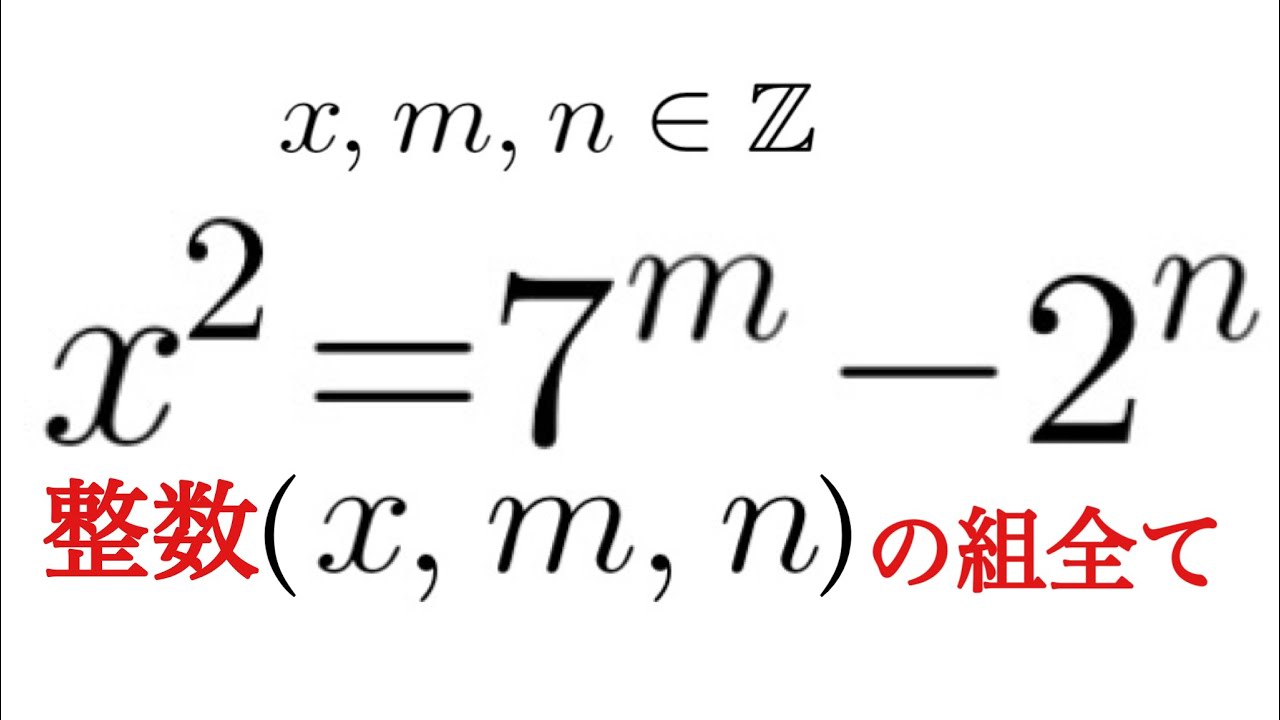
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
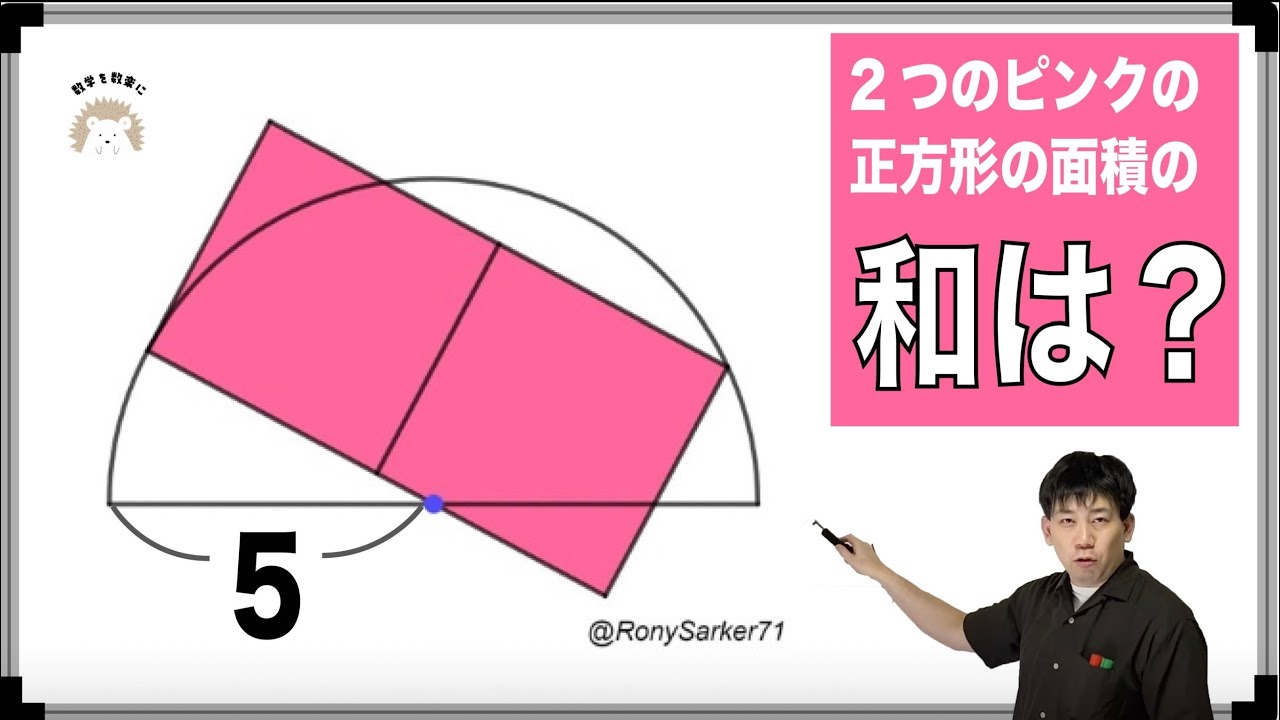
整数$x,m,n$を全て求めよ.
$x^2=7^m-2^n$
この動画を見る
整数$x,m,n$を全て求めよ.
$x^2=7^m-2^n$
【高校数学】1次不定方程式~自分に合った解き方を身に付けよう~ 5-9【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$45x+32y=4$の整数解をすべて求めよ
この動画を見る
$45x+32y=4$の整数解をすべて求めよ
【共通テスト】数学IA 第2問を瞬時に解くテクニックを解説します(2021.本試験)

単元:
#数Ⅰ#数A#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
この動画を見る
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
ガウス記号

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\left[\dfrac{x^2+1}{10}\right]+\left[\dfrac{10}{x^2+1}\right]=1$
この動画を見る
これを解け.
$\left[\dfrac{x^2+1}{10}\right]+\left[\dfrac{10}{x^2+1}\right]=1$
福田のわかった数学〜高校1年生091〜確率(11)反復試行の確率(5)東京大学の問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(11) 反復試行(5)
格子点上を次の規則で点$\textrm{P}$が動く。
$(\textrm{a})$最初、点$\textrm{P}$は原点にある。
$(\textrm{b})$ある時刻で点$\textrm{P}$が(m,n)にあるとき、その1秒後の点$\textrm{P}$の位置は等確率で
$(m+1,n), (m,n+1), (m,n-1), (m-1,n)$である。
6秒後に点$\textrm{P}$が直線$y=x$上にある確率を求めよ。
東京大学過去問
この動画を見る
数学$\textrm{A}$ 確率(11) 反復試行(5)
格子点上を次の規則で点$\textrm{P}$が動く。
$(\textrm{a})$最初、点$\textrm{P}$は原点にある。
$(\textrm{b})$ある時刻で点$\textrm{P}$が(m,n)にあるとき、その1秒後の点$\textrm{P}$の位置は等確率で
$(m+1,n), (m,n+1), (m,n-1), (m-1,n)$である。
6秒後に点$\textrm{P}$が直線$y=x$上にある確率を求めよ。
東京大学過去問
モスクワ数学オリンピック 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n・2^n+1$が3の倍数となる自然数$n$を求めよ.
数学オリンピックモスクワ過去問
この動画を見る
$n・2^n+1$が3の倍数となる自然数$n$を求めよ.
数学オリンピックモスクワ過去問
どっちがでかい? エレガントな解法も
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
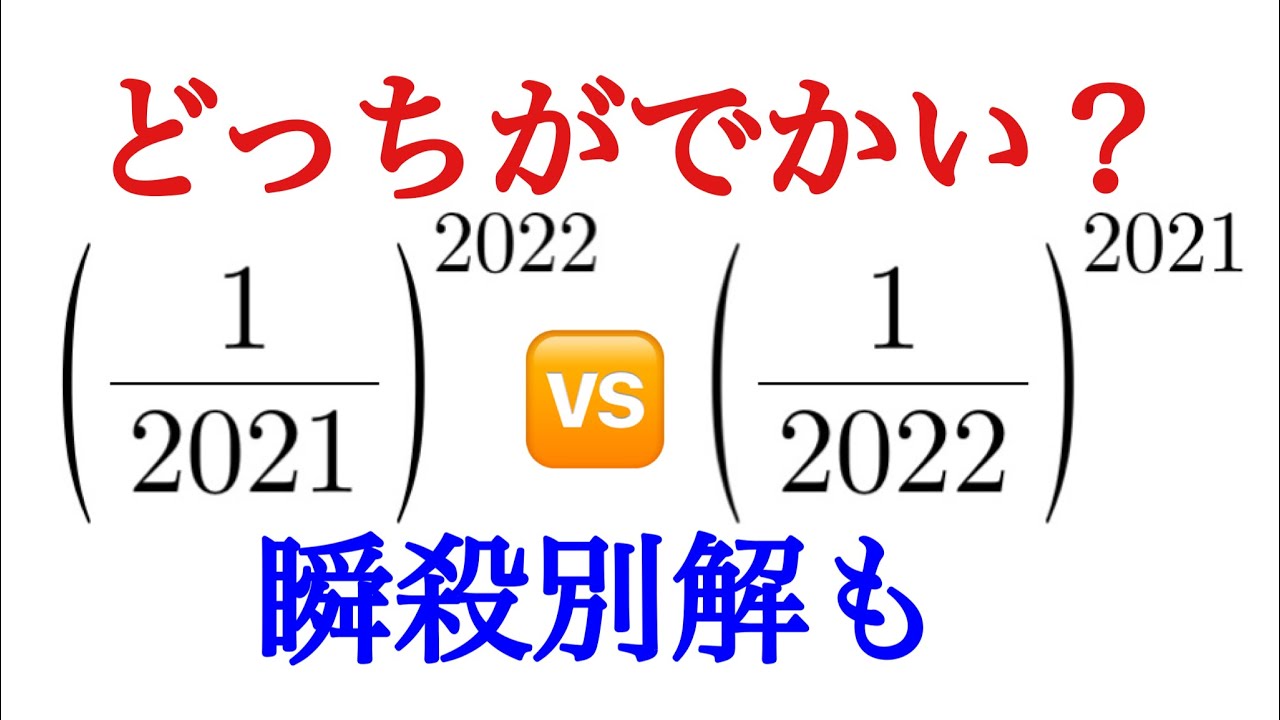
どちらが大きいか?
$\left(\dfrac{1}{2021}\right)^{2022}$VS $\left(\dfrac{1}{2022}\right)^{2021}$
この動画を見る
どちらが大きいか?
$\left(\dfrac{1}{2021}\right)^{2022}$VS $\left(\dfrac{1}{2022}\right)^{2021}$
共通テスト数学1A_第1問を簡単に解く方法教えます

単元:
#数Ⅰ#数A#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
[1]$c$を正の整数とする。$x$の2次方程式
$2x^2+(4c-3)x+2c^2-c-11=0$ について考える。
(1)$c=1$のとき、①の左辺を因数分解すると
$([ア]x+[イ])(x-[ウ])$
であるから、①の解は
$x=-\displaystyle \frac{[イ]}{[ア]},[ウ]$である。
(2)$c=2$のとき、①の解は
$x=\displaystyle \frac{-[エ] \pm \sqrt{ [オカ] }}{[キ]}$
であり、大きい方の解を$a$とすると
$\displaystyle \frac{5}{a}=\displaystyle \frac{[ク] + \sqrt{ [ケコ] }}{[サ]}$
である。また、$m<\displaystyle \frac{5}{a}<m+1$を満たす整数は[シ]である。
(3)太郎さんと花子さんは、①の解について考察している。
-----------------
太郎:①の解は$c$の値によって、ともに有理数である場合もあれば、
ともに無理数である場合もあるね。
$c$がどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
-----------------
①の解が異なる二つの有理数であるような正の整数$c$の個数は[ス]個である。
この動画を見る
[1]$c$を正の整数とする。$x$の2次方程式
$2x^2+(4c-3)x+2c^2-c-11=0$ について考える。
(1)$c=1$のとき、①の左辺を因数分解すると
$([ア]x+[イ])(x-[ウ])$
であるから、①の解は
$x=-\displaystyle \frac{[イ]}{[ア]},[ウ]$である。
(2)$c=2$のとき、①の解は
$x=\displaystyle \frac{-[エ] \pm \sqrt{ [オカ] }}{[キ]}$
であり、大きい方の解を$a$とすると
$\displaystyle \frac{5}{a}=\displaystyle \frac{[ク] + \sqrt{ [ケコ] }}{[サ]}$
である。また、$m<\displaystyle \frac{5}{a}<m+1$を満たす整数は[シ]である。
(3)太郎さんと花子さんは、①の解について考察している。
-----------------
太郎:①の解は$c$の値によって、ともに有理数である場合もあれば、
ともに無理数である場合もあるね。
$c$がどのような値のときに、解は有理数になるのかな。
花子:2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。
-----------------
①の解が異なる二つの有理数であるような正の整数$c$の個数は[ス]個である。
福田のわかった数学〜高校1年生090〜確率(10)反復試行の確率(4)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(10) 反復試行(4)
正六角形ABCDEFの頂点Aに石を置いて、コインを投げて
表が出れば2、裏が出れば1、石を時計周りに動かし、最初に
Aに戻った時を上がりとする。次の確率を求めよ。
(1)ちょうど1周で上がり (2)ちょうど2周で上がり
この動画を見る
数学$\textrm{A}$ 確率(10) 反復試行(4)
正六角形ABCDEFの頂点Aに石を置いて、コインを投げて
表が出れば2、裏が出れば1、石を時計周りに動かし、最初に
Aに戻った時を上がりとする。次の確率を求めよ。
(1)ちょうど1周で上がり (2)ちょうど2周で上がり
整数問題 あの定理の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2P^4-1237$が素数となる素数$P$をすべて求めよ.
この動画を見る
$2P^4-1237$が素数となる素数$P$をすべて求めよ.
独協医大 n進法

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0.2_{(a)}=0.12_{(b)}$
$a,b$の値を求めよ.
独協医大過去問
この動画を見る
$0.2_{(a)}=0.12_{(b)}$
$a,b$の値を求めよ.
独協医大過去問
福田のわかった数学〜高校1年生089〜確率(9)反復試行の確率(3)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(9) 反復試行(3)
点Pをxy平面上の原点におき、次の規則で動かす。
さいころを1回振るごとに
1,2,3の目が出たらx軸方向へ1平行移動
4,5の目が出たらy軸方向へ1平行移動
6の目が出たらx軸方向へ1、y軸方向へ1平行移動
さいころを6回振って点Pが(5,3)に位置する確率を求めよ。
この動画を見る
数学$\textrm{A}$ 確率(9) 反復試行(3)
点Pをxy平面上の原点におき、次の規則で動かす。
さいころを1回振るごとに
1,2,3の目が出たらx軸方向へ1平行移動
4,5の目が出たらy軸方向へ1平行移動
6の目が出たらx軸方向へ1、y軸方向へ1平行移動
さいころを6回振って点Pが(5,3)に位置する確率を求めよ。
福田のわかった数学〜高校1年生088〜確率(8)反復試行の確率(2)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(7) 反復試行(2)
AとBが先に4勝したほうを勝ちとする試合をする。
1回の試合でAが勝つ確率をpとして引き分けはないものとする。
(1)6試合目でAが勝つ確率を求めよ。
(2)Aが勝つ確率を求めよ。
この動画を見る
数学$\textrm{A}$ 確率(7) 反復試行(2)
AとBが先に4勝したほうを勝ちとする試合をする。
1回の試合でAが勝つ確率をpとして引き分けはないものとする。
(1)6試合目でAが勝つ確率を求めよ。
(2)Aが勝つ確率を求めよ。
#48 数検1級2次 過去問 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n$:正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
この動画を見る
$m,n$:正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
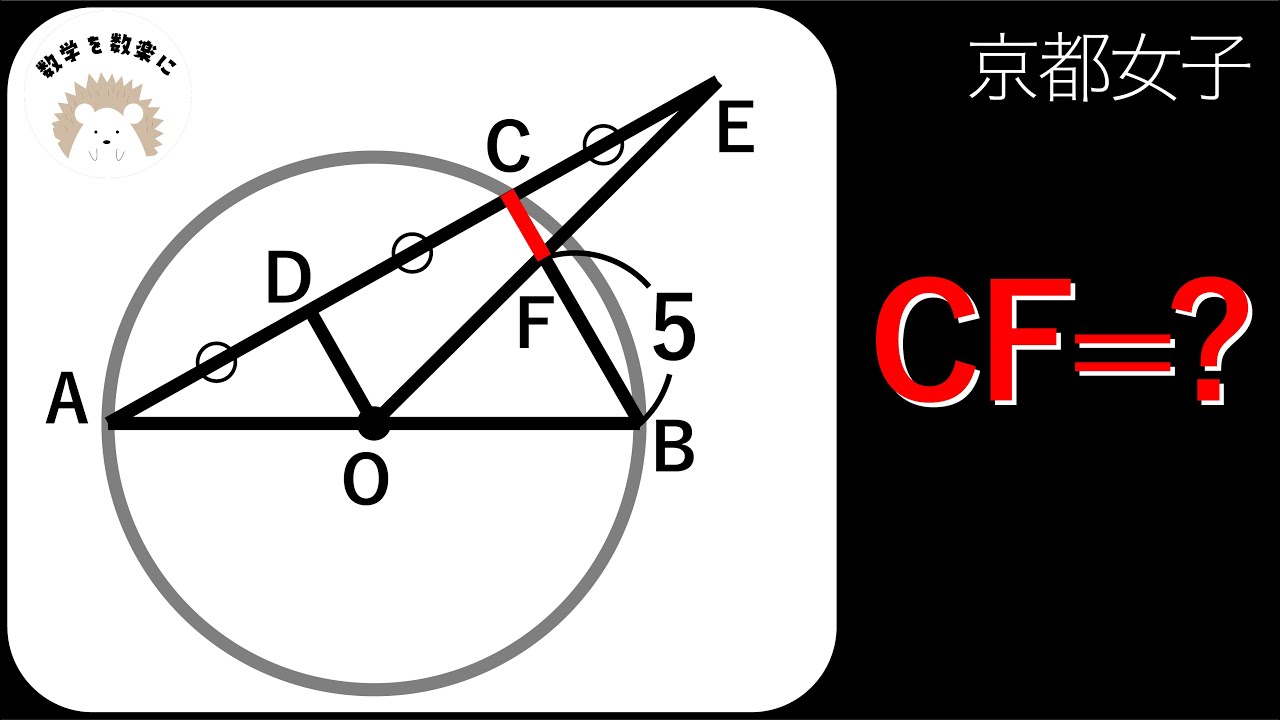
2通りで解説!!京都女子
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
CF=?
*図は動画内参照
京都女子高等学校
この動画を見る
CF=?
*図は動画内参照
京都女子高等学校
中学入試・高校入試頻出メネラウスの定理は使う?
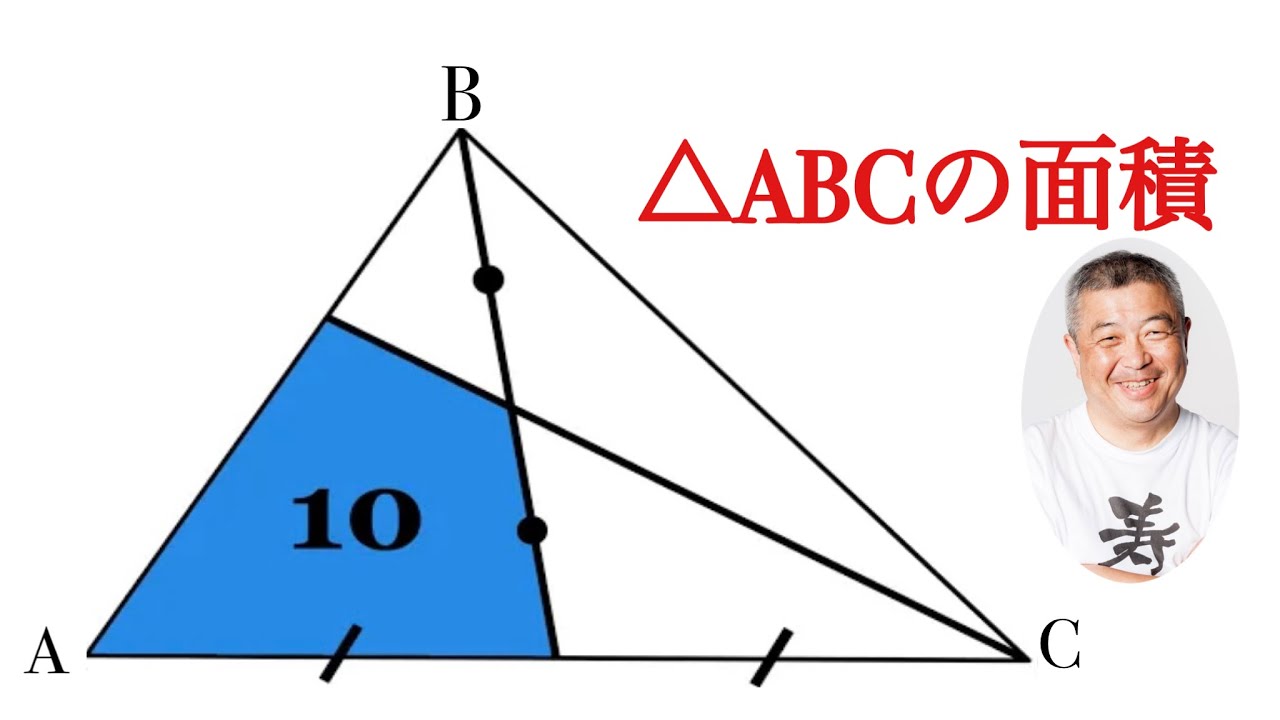
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
メネラウスの定理が定期試験に出る頻度に関して解説していきます.
この動画を見る
メネラウスの定理が定期試験に出る頻度に関して解説していきます.
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$27^x-2・18^x+12^x=8^{x+\frac{1}{3}}$
この動画を見る
実数解を求めよ.
$27^x-2・18^x+12^x=8^{x+\frac{1}{3}}$
福田のわかった数学〜高校1年生087〜確率(7)反復試行の確率(1)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(7) 反復試行(1)
さいころをn回振った時に
(1)1の目がr回出る確率を求めよ。
(2)1の目がj回、2の目がk回出る確率を求めよ。
この動画を見る
数学$\textrm{A}$ 確率(7) 反復試行(1)
さいころをn回振った時に
(1)1の目がr回出る確率を求めよ。
(2)1の目がj回、2の目がk回出る確率を求めよ。
角度が出てないのに角度が出る問題 渋谷教育学園幕張高校
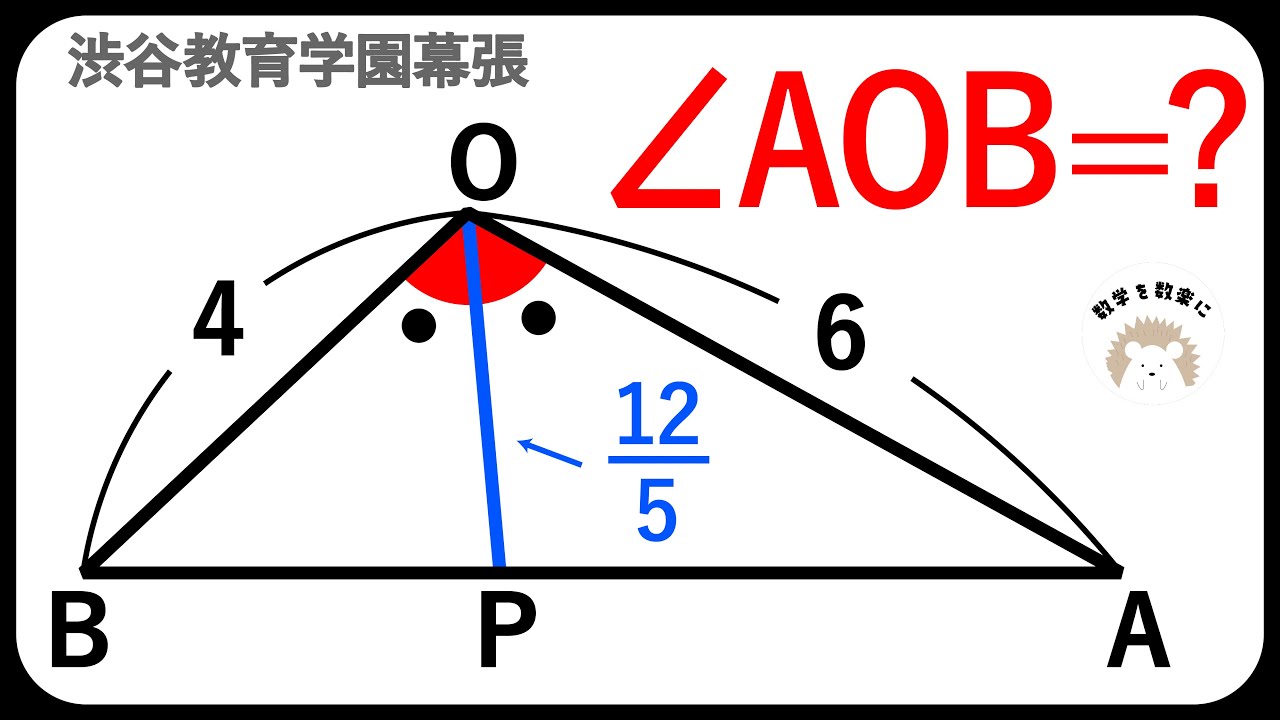
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle AOB =?$
*図は動画内参照
渋谷教育学園幕張高校
この動画を見る
$\angle AOB =?$
*図は動画内参照
渋谷教育学園幕張高校
ざ・見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{10000}n^n$
$=1^1+2^2+3^3+・・・・・・9999^{9999}+10000^{10000}$を3で割った余りを求めよ.
この動画を見る
$\displaystyle \sum_{n=1}^{10000}n^n$
$=1^1+2^2+3^3+・・・・・・9999^{9999}+10000^{10000}$を3で割った余りを求めよ.
福田のわかった数学〜高校1年生086〜確率(6)じゃんけんの確率(2)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(6) じゃんけん(2)
4人でじゃんけんをして負けたもの
から抜けていく。3回で1人の勝者
が決まる確率を求めよ。
この動画を見る
数学$\textrm{A}$ 確率(6) じゃんけん(2)
4人でじゃんけんをして負けたもの
から抜けていく。3回で1人の勝者
が決まる確率を求めよ。
直角に凹ませました

変な指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
この動画を見る
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
整数問題 愛知高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1から9までの自然数から異なる2つを選びa,bとする。(a<b)
$\frac{1}{a} - \frac{1}{b}$の値が最も小さくなるa,bを求めよ。
愛知高等学校
この動画を見る
1から9までの自然数から異なる2つを選びa,bとする。(a<b)
$\frac{1}{a} - \frac{1}{b}$の値が最も小さくなるa,bを求めよ。
愛知高等学校
補助線どう引く?
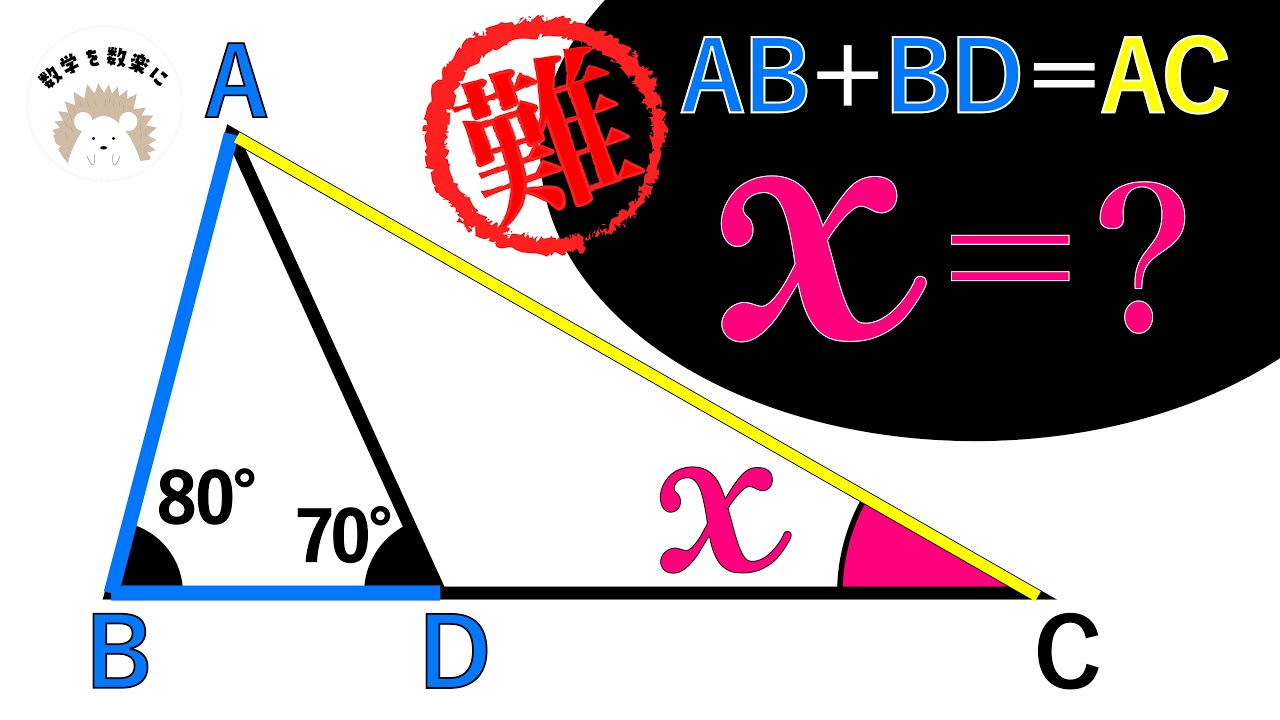
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB+BD=AC
x=?
*図は動画内参照
この動画を見る
AB+BD=AC
x=?
*図は動画内参照
福田のわかった数学〜高校1年生085〜確率(5)じゃんけんの確率(1)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(4) じゃんけん(1)
n人でじゃんけんを1回する。 $(n \geqq 3)$
(1)r人が勝つ確率を求めよ。 $(0 \lt r \lt n)$
(2)あいこになる確率を求めよ。
この動画を見る
数学$\textrm{A}$ 確率(4) じゃんけん(1)
n人でじゃんけんを1回する。 $(n \geqq 3)$
(1)r人が勝つ確率を求めよ。 $(0 \lt r \lt n)$
(2)あいこになる確率を求めよ。
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
この動画を見る
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
