 数A
数A
 数A
数A
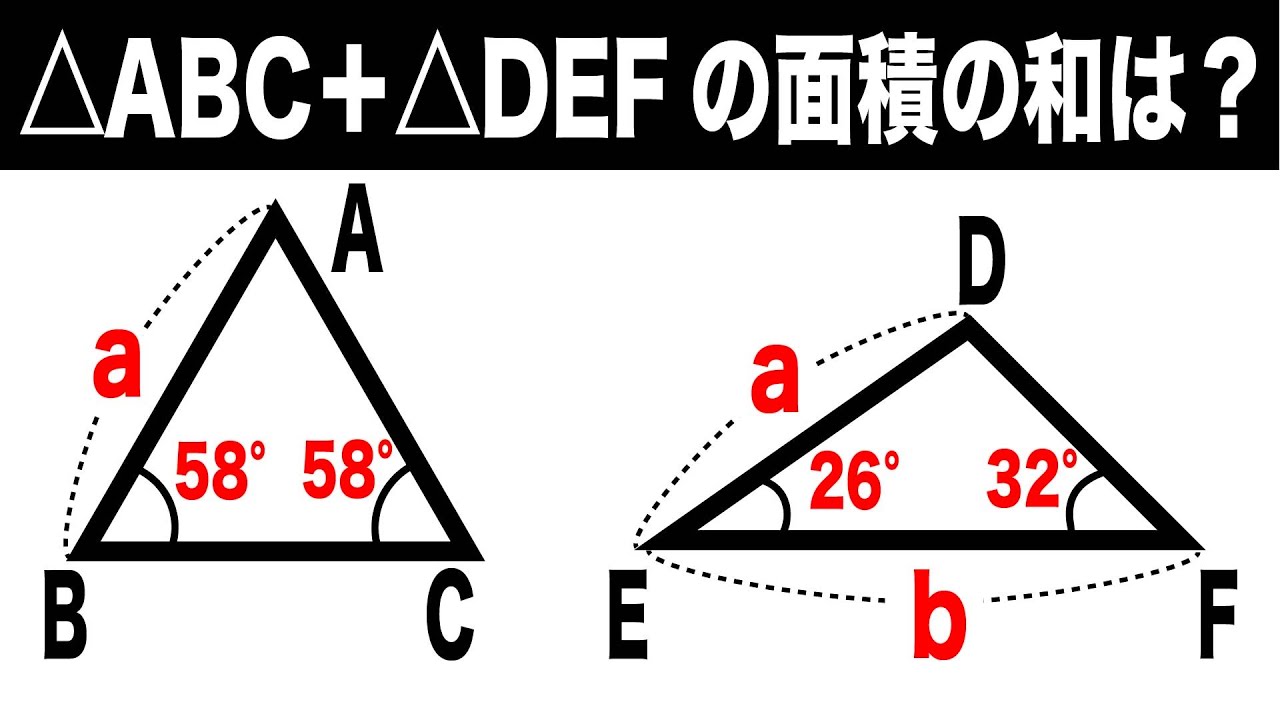
面積の和=❓
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC+△DEF=?(面積の和)
*図は動画内参照
この動画を見る
△ABC+△DEF=?(面積の和)
*図は動画内参照
【数A】整数の性質:東京大学(理系)2003年 第4問

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次方程式$x^2-4x+1=0$の2つの実数解のうち大きいものを$\alpha$,小さいものを$\beta$とす る。$n=1,2,3,...$に対し、$s_n=\alpha^n+\beta^n$とおく。
(1)$s_1,s_2,s_3$を求めよ。ま た、$n\geqq 3$に対し、$s_n$を$s_{n-1}$と$s_{n-2}$で表そう。
(2)$\beta^3$以下の最大の整数を求め よ。
(3)$\alpha^{2003}$以下の最大の整数の1の位の数を求めよ。
この動画を見る
2次方程式$x^2-4x+1=0$の2つの実数解のうち大きいものを$\alpha$,小さいものを$\beta$とす る。$n=1,2,3,...$に対し、$s_n=\alpha^n+\beta^n$とおく。
(1)$s_1,s_2,s_3$を求めよ。ま た、$n\geqq 3$に対し、$s_n$を$s_{n-1}$と$s_{n-2}$で表そう。
(2)$\beta^3$以下の最大の整数を求め よ。
(3)$\alpha^{2003}$以下の最大の整数の1の位の数を求めよ。
整数問題 大阪教育大附属天王寺

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数A,B,Cを求めよ。
$
\begin{eqnarray}
\left\{
\begin{array}{l}
A \div B \times C=12 \\
A \div B - C=1 \\
A \div B =10
\end{array}
\right.
\end{eqnarray}
$
大阪教育大学附属高等学校天王寺校舎
この動画を見る
自然数A,B,Cを求めよ。
$
\begin{eqnarray}
\left\{
\begin{array}{l}
A \div B \times C=12 \\
A \div B - C=1 \\
A \div B =10
\end{array}
\right.
\end{eqnarray}
$
大阪教育大学附属高等学校天王寺校舎
【数A】整数の性質:○○でないの証明は背理法

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
pが素数のとき、$1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{p}$は整数でないことを証明しよう。
この動画を見る
pが素数のとき、$1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{p}$は整数でないことを証明しよう。
ただの累乗根方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt[x]{4096}-\sqrt[\frac{x}{2}]{2^{3x-6}}+12=0$
この動画を見る
これを解け.
$\sqrt[x]{4096}-\sqrt[\frac{x}{2}]{2^{3x-6}}+12=0$
座標平面 円 角度
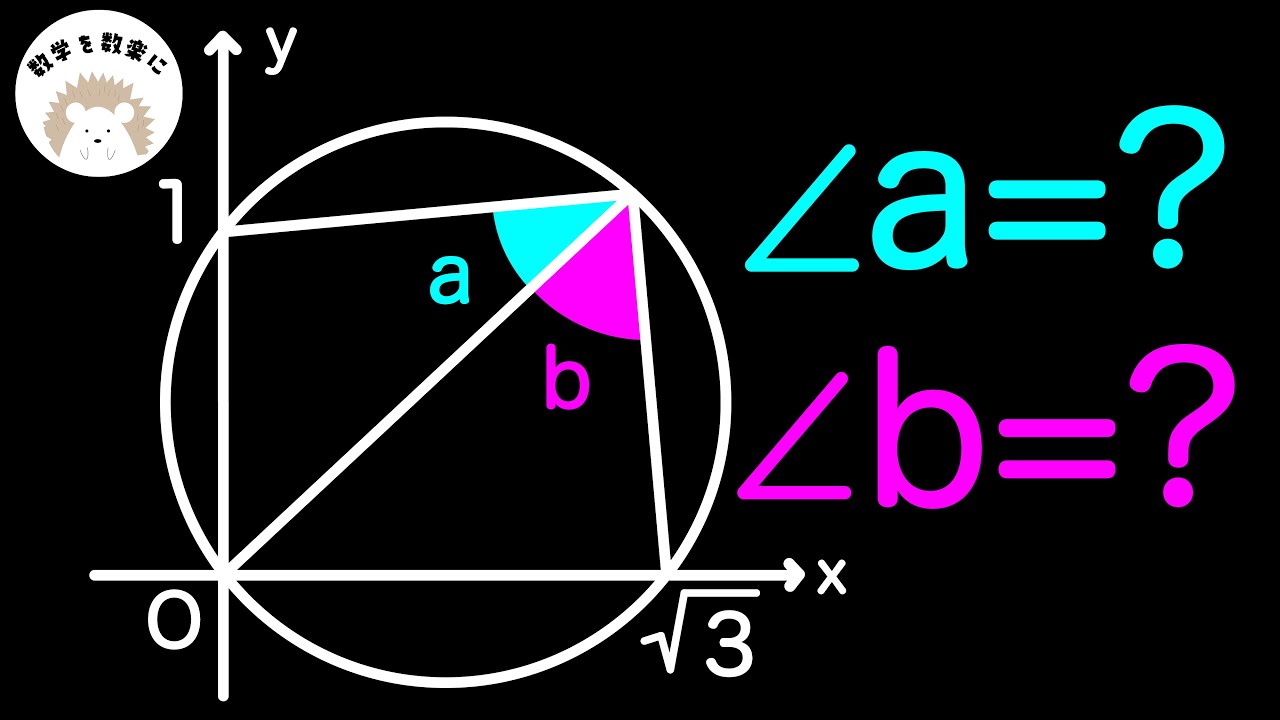
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a=?$
$\angle b=?$
*図は動画内参照
この動画を見る
$\angle a=?$
$\angle b=?$
*図は動画内参照
17和歌山県教員採用試験(数学:1-(5) 確率)

単元:
#数A#場合の数と確率#確率#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
サイコロを3回投げ,
出た目を順に$a,b,c$とする.
$abx^2-12x+c=0$が
重解をもつ確率を求めよ.
この動画を見る
$\boxed{6}$
サイコロを3回投げ,
出た目を順に$a,b,c$とする.
$abx^2-12x+c=0$が
重解をもつ確率を求めよ.
連立二元二次方程式
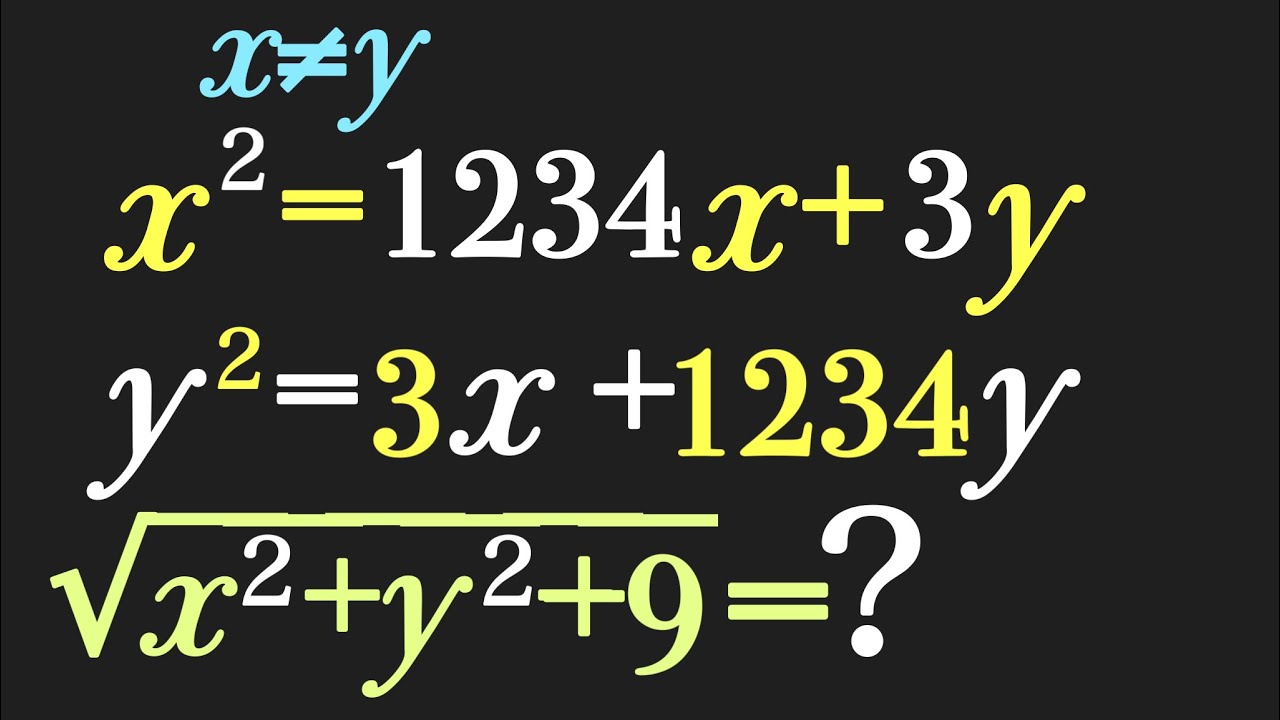
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
この動画を見る
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
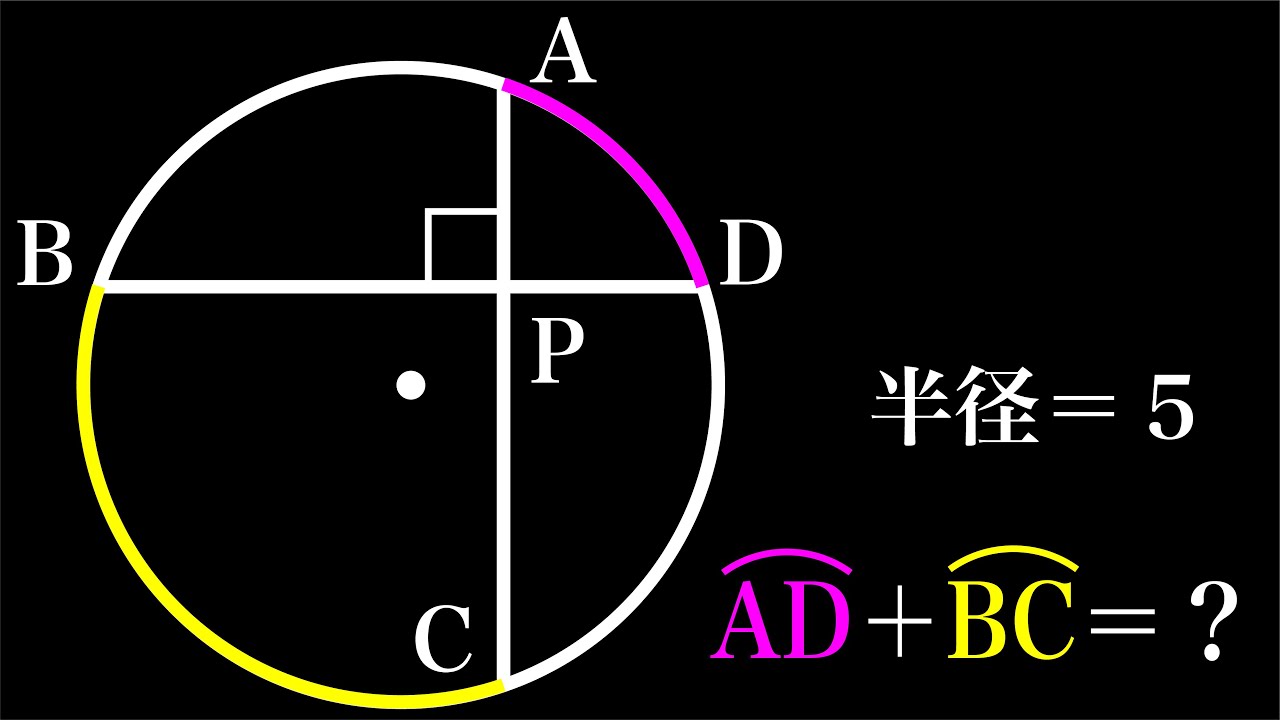
弧の長さの和=❓
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AB}+\stackrel{\huge\frown}{BC} =?$
*図は動画内参照
この動画を見る
$\stackrel{\huge\frown}{AB}+\stackrel{\huge\frown}{BC} =?$
*図は動画内参照
有名問題だよ(多分)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[n]{n}$が最大となる自然数$n$を求めよ.
この動画を見る
$\sqrt[n]{n}$が最大となる自然数$n$を求めよ.
福田の数学〜早稲田大学2021年人間科学部第2問(3)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
この動画を見る
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{70} \mathrm{C}_{35}$を$71$で割った余りを求めよ.
${}_{50} \mathrm{C}_{25}$を$51$で割った余りを求めよ.
この動画を見る
${}_{70} \mathrm{C}_{35}$を$71$で割った余りを求めよ.
${}_{50} \mathrm{C}_{25}$を$51$で割った余りを求めよ.
福田の数学〜早稲田大学2021年人間科学部第1問〜異なるペアになる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(1)8人のメンバーで、2人組(ペア)を4組作る方法は$n$通りある。$n$を$100$で割った商は$\boxed{\ \ ア\ \ }$で、余りは$\boxed{\ \ イ\ \ }$である。
(2)8人のメンバーで、2人組(ペア)を4組作って、ある作業に取り組んだ後、同じ8人で次の作業に取り組むペアを作るために、くじ引きをした。このとき、8人全員がくじ引き前と異なるメンバーとペアになる確率は$\dfrac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$ である。
ただし、くじは公平でどの2人もペアになる確率は等しいものとする。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{1}}$
(1)8人のメンバーで、2人組(ペア)を4組作る方法は$n$通りある。$n$を$100$で割った商は$\boxed{\ \ ア\ \ }$で、余りは$\boxed{\ \ イ\ \ }$である。
(2)8人のメンバーで、2人組(ペア)を4組作って、ある作業に取り組んだ後、同じ8人で次の作業に取り組むペアを作るために、くじ引きをした。このとき、8人全員がくじ引き前と異なるメンバーとペアになる確率は$\dfrac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$ である。
ただし、くじは公平でどの2人もペアになる確率は等しいものとする。
2021早稲田大学人間科学部過去問
16和歌山県教員採用試験(数学:5番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$n$が整数のとき,
$2n^3-3n^2+n$は6の倍数であることを示せ.
この動画を見る
$\boxed{5}$
$n$が整数のとき,
$2n^3-3n^2+n$は6の倍数であることを示せ.
福田の数学〜早稲田大学2021年商学部第3問〜正の約数の総和が奇数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ 次の設問に答えよ。
(1)$225$の全ての正の約数の和を求めよ。
(2)$2021$以下の正の整数で、すべての正の約数の和が奇数であるものの個数を求めよ。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{3}}$ 次の設問に答えよ。
(1)$225$の全ての正の約数の和を求めよ。
(2)$2021$以下の正の整数で、すべての正の約数の和が奇数であるものの個数を求めよ。
2021早稲田大学商学部過去問
【数A】場合の数:2021年高3第1回K塾記述模試

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
白玉6個、赤玉2個、青玉2個の計10個の玉を横一列に並べる。ただし、同じ色の玉は区別しない。
(1)並べ方は全部で何通りあるか。
(2)白赤白赤白と連続して並ぶ箇所があるような並べ方は何通りあるか。
(3)次の、赤玉についての条件A、青玉についての条件Bを考える。
A:「同じ色の玉が両隣にある」
B:「異なる色の玉が 両隣にある」
ただし、列の両端の玉は、AもBも満たさないものとする。例えば、 白赤白白白青赤青白白は、2個の赤玉はともにAを満たし、2個の青玉もともにBを 満たす。また、白赤赤白白青青白白白は、2個の青玉はともにBを満たすが、2個 の赤玉はともにAを満たさない。
(i)2個の赤玉がともにAを満たすような並べ方は 何通りあるか。
(ii)2個の赤玉がともにAを満たし、かつ、2個の青玉がともにBを満たすような並べ方は何通りあるか。
この動画を見る
白玉6個、赤玉2個、青玉2個の計10個の玉を横一列に並べる。ただし、同じ色の玉は区別しない。
(1)並べ方は全部で何通りあるか。
(2)白赤白赤白と連続して並ぶ箇所があるような並べ方は何通りあるか。
(3)次の、赤玉についての条件A、青玉についての条件Bを考える。
A:「同じ色の玉が両隣にある」
B:「異なる色の玉が 両隣にある」
ただし、列の両端の玉は、AもBも満たさないものとする。例えば、 白赤白白白青赤青白白は、2個の赤玉はともにAを満たし、2個の青玉もともにBを 満たす。また、白赤赤白白青青白白白は、2個の青玉はともにBを満たすが、2個 の赤玉はともにAを満たさない。
(i)2個の赤玉がともにAを満たすような並べ方は 何通りあるか。
(ii)2個の赤玉がともにAを満たし、かつ、2個の青玉がともにBを満たすような並べ方は何通りあるか。
福田の数学〜早稲田大学2021年商学部第2問〜空間図形の共通部分

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
変わった指数方程式
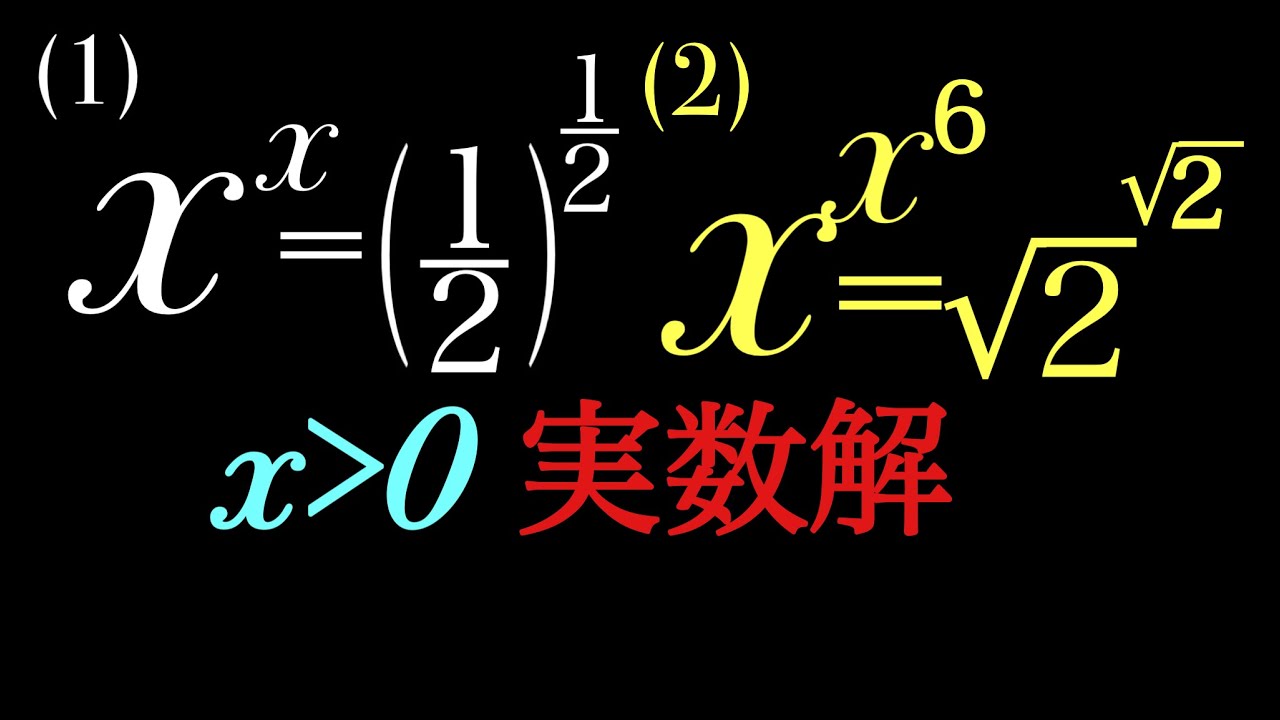
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$である.これを解け.
(1)$x^x=\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$
(2)$x^{x^6}=\sqrt2^{\sqrt2}$
この動画を見る
$x\gt 0$である.これを解け.
(1)$x^x=\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$
(2)$x^{x^6}=\sqrt2^{\sqrt2}$
3の倍数はどれ? 大阪府 A

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
値がつねに3の倍数になるものはどれ?(n:自然数)
ア $n+3$
イ $3(n+1)$
ウ $\frac{1}{3}n$
エ $6n$
オ $2n^2+1$
大阪府
この動画を見る
値がつねに3の倍数になるものはどれ?(n:自然数)
ア $n+3$
イ $3(n+1)$
ウ $\frac{1}{3}n$
エ $6n$
オ $2n^2+1$
大阪府
福田の数学〜早稲田大学2021年商学部第1問(4)〜空間内の点の移動の場合の数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(4)座標空間において、各座標が整数である6個の点$\rm P_0,P_1,P_2,P_3,P_4,P_5$を、次の条件を満たすように重複を許して選ぶ。
$(\textrm{i}) \rm P_0=(0,0,0)$
$(\textrm{ii})$ ${\rm P}_k$と${\rm P}_{k+1}$との距離は$1$$ (k=0,1,2,3,4,5)$
$(\textrm{iii})$ ${\rm P}_0$と${\rm P}_5$との距離は$1$
このとき、選び方の総数は$\boxed{\ \ エ\ \ }$通りである。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(4)座標空間において、各座標が整数である6個の点$\rm P_0,P_1,P_2,P_3,P_4,P_5$を、次の条件を満たすように重複を許して選ぶ。
$(\textrm{i}) \rm P_0=(0,0,0)$
$(\textrm{ii})$ ${\rm P}_k$と${\rm P}_{k+1}$との距離は$1$$ (k=0,1,2,3,4,5)$
$(\textrm{iii})$ ${\rm P}_0$と${\rm P}_5$との距離は$1$
このとき、選び方の総数は$\boxed{\ \ エ\ \ }$通りである。
2021早稲田大学商学部過去問
【数A】図形の性質:高3 5月K塾共通テスト 数学IA第5問

単元:
#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#センター試験・共通テスト関連#全統模試(河合塾)#共通テスト#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCにおいて、$AB=3,AC=6,\angle BAC=90°$であるとき、$BC=(ア)\sqrt{(イ)}$である。Aを中心とし、Bを通る円をKとし、円Kと直線ACの交点のうち辺AC上にある方をD、もう一方をEとする。また、円Kと直線BCの交点でBと異なるものをFとする。このとき、CE=(ウ)であり、方べきの定理を用いると、$CF=\dfrac{(エ)\sqrt{(オ)}}{(カ)}$とわかるから$\dfrac{BF}{FC}=\dfrac{(キ)}{(ク)}$である。さらに、直線EFと辺ABの交点をP、直線EFと線分BCの交点をQとすると、$\dfrac{BQ}{QD}=(ケ)$であり、△BFQの面積は$\dfrac{(コ)}{(サシ)}$である。また、△CPQの面積は$\dfrac{(ス)}{(セ)}$である。
この動画を見る
△ABCにおいて、$AB=3,AC=6,\angle BAC=90°$であるとき、$BC=(ア)\sqrt{(イ)}$である。Aを中心とし、Bを通る円をKとし、円Kと直線ACの交点のうち辺AC上にある方をD、もう一方をEとする。また、円Kと直線BCの交点でBと異なるものをFとする。このとき、CE=(ウ)であり、方べきの定理を用いると、$CF=\dfrac{(エ)\sqrt{(オ)}}{(カ)}$とわかるから$\dfrac{BF}{FC}=\dfrac{(キ)}{(ク)}$である。さらに、直線EFと辺ABの交点をP、直線EFと線分BCの交点をQとすると、$\dfrac{BQ}{QD}=(ケ)$であり、△BFQの面積は$\dfrac{(コ)}{(サシ)}$である。また、△CPQの面積は$\dfrac{(ス)}{(セ)}$である。
【数A】整数の性質:高3 5月K塾共通テスト 数学IA第4問

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#全統模試(河合塾)#共通テスト#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)168を素因数分解すると 168=(ア)^(イ)×3×(ウ) である。
よって、168の正の約数の個数は(エオ)個であり、AB=168かつ3≦A<Bを満たすA,Bの組は、全部で(カ)個である。
(2)正の整数nは正の約数の個数が6個であり、正の約数の総和が168であるとする。このような正の整数nのうち、異なる2つの素因数を持つものを求めよう。
nは異なる素数p,qを用いて、n=p^(キ)・q と表せる。
このとき、nの正の約数の総和は[ク]であるから、p=(ケ) であり、n=(コサ) である。
[ク]の解答群
0: (p+p²)q
1: (1+p+p²)q
2: (p+p²)(1+q)
3: (1+p+p²)(1+q)
4: (p+p²+p³)q
5: (1+p+p²+p³)q
6: (p+p²+p³)(1+q)
7: (1+p+p²+p³)(1+q)
(3)正の整数mは正の約数の個数が12個であり、正の約数の総和が624であるとする。このような正の整数mのうち、異なる3つの素因数を持つものは m=(シスセ) である。
この動画を見る
(1)168を素因数分解すると 168=(ア)^(イ)×3×(ウ) である。
よって、168の正の約数の個数は(エオ)個であり、AB=168かつ3≦A<Bを満たすA,Bの組は、全部で(カ)個である。
(2)正の整数nは正の約数の個数が6個であり、正の約数の総和が168であるとする。このような正の整数nのうち、異なる2つの素因数を持つものを求めよう。
nは異なる素数p,qを用いて、n=p^(キ)・q と表せる。
このとき、nの正の約数の総和は[ク]であるから、p=(ケ) であり、n=(コサ) である。
[ク]の解答群
0: (p+p²)q
1: (1+p+p²)q
2: (p+p²)(1+q)
3: (1+p+p²)(1+q)
4: (p+p²+p³)q
5: (1+p+p²+p³)q
6: (p+p²+p³)(1+q)
7: (1+p+p²+p³)(1+q)
(3)正の整数mは正の約数の個数が12個であり、正の約数の総和が624であるとする。このような正の整数mのうち、異なる3つの素因数を持つものは m=(シスセ) である。
【数A】確率:高3 5月K塾共通テスト 数学IA第3問

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#全統模試(河合塾)#共通テスト#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個のさいころを繰り返し投げ、次の規則に従って数直線上の点Pを動かす。
・原点から出発して、1回目に出た目の数だけ点Pを負の方向に動かす。
・1回目で点Pがとまった位置から出発して、2回目に出た目の数だけ点Pを正の方向に動かす。
・2回目で点Pがとまった位置から出発して、3回目に出た目の数だけ点Pを負の方向に動かす。
・以下同様に、直前の回で点Pgaとまった位置から出発して、奇数回目の移動では出た目の数だけ点Pを負の方向に動かし、偶数回目の移動では出た目の数だけ点Pを正の方向に動かす。
例えば、さいころを4回投げて順に5,5,2,6の目が出た場合、点Pの座標は順に、-5,0,-2,4となる。
(1)2回目の移動後に点Pの座標が0となる確率は(ア)/(イ)、4となる確率は(ウ)/(エオ)、5となる確率は(カ)/(キク)である。
(2)4回目の移動後に点Pの座標が9となるのは、点Pの座標が2回目の移動後に(ケ)となり、4回目の移動後に9となる場合、または点Pの座標が2回目の移動後に(コ)となり、4回目の移動後に9となる場合のいずれかである。ただし、(ケ)と(コ)の順序は問わない。
よって、4回目の移動後に点Pの座標が9となる確率は(サ)/(シスセ)である。
また、4回目の移動後に点Pの座標が9であったとき、3回目の移動後の点Pの座標が4である条件付き確率は(ソ)/(タ)である。
(3)7回目の移動後に点Pの座標が13となる確率は(チ)/(ツ)^(テ)である。
この動画を見る
1個のさいころを繰り返し投げ、次の規則に従って数直線上の点Pを動かす。
・原点から出発して、1回目に出た目の数だけ点Pを負の方向に動かす。
・1回目で点Pがとまった位置から出発して、2回目に出た目の数だけ点Pを正の方向に動かす。
・2回目で点Pがとまった位置から出発して、3回目に出た目の数だけ点Pを負の方向に動かす。
・以下同様に、直前の回で点Pgaとまった位置から出発して、奇数回目の移動では出た目の数だけ点Pを負の方向に動かし、偶数回目の移動では出た目の数だけ点Pを正の方向に動かす。
例えば、さいころを4回投げて順に5,5,2,6の目が出た場合、点Pの座標は順に、-5,0,-2,4となる。
(1)2回目の移動後に点Pの座標が0となる確率は(ア)/(イ)、4となる確率は(ウ)/(エオ)、5となる確率は(カ)/(キク)である。
(2)4回目の移動後に点Pの座標が9となるのは、点Pの座標が2回目の移動後に(ケ)となり、4回目の移動後に9となる場合、または点Pの座標が2回目の移動後に(コ)となり、4回目の移動後に9となる場合のいずれかである。ただし、(ケ)と(コ)の順序は問わない。
よって、4回目の移動後に点Pの座標が9となる確率は(サ)/(シスセ)である。
また、4回目の移動後に点Pの座標が9であったとき、3回目の移動後の点Pの座標が4である条件付き確率は(ソ)/(タ)である。
(3)7回目の移動後に点Pの座標が13となる確率は(チ)/(ツ)^(テ)である。
ドーナッツの面積再び!!

福田のわかった数学〜高校1年生030〜ガウス記号を含んだ方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{I} ガウス記号を含む方程式\\
次の方程式を解け。\\
(1)[2x]^2=4 (2)[2x]=[x]
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} ガウス記号を含む方程式\\
次の方程式を解け。\\
(1)[2x]^2=4 (2)[2x]=[x]
\end{eqnarray}
空間図形 垂直について 簡単だけど大切です。
単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
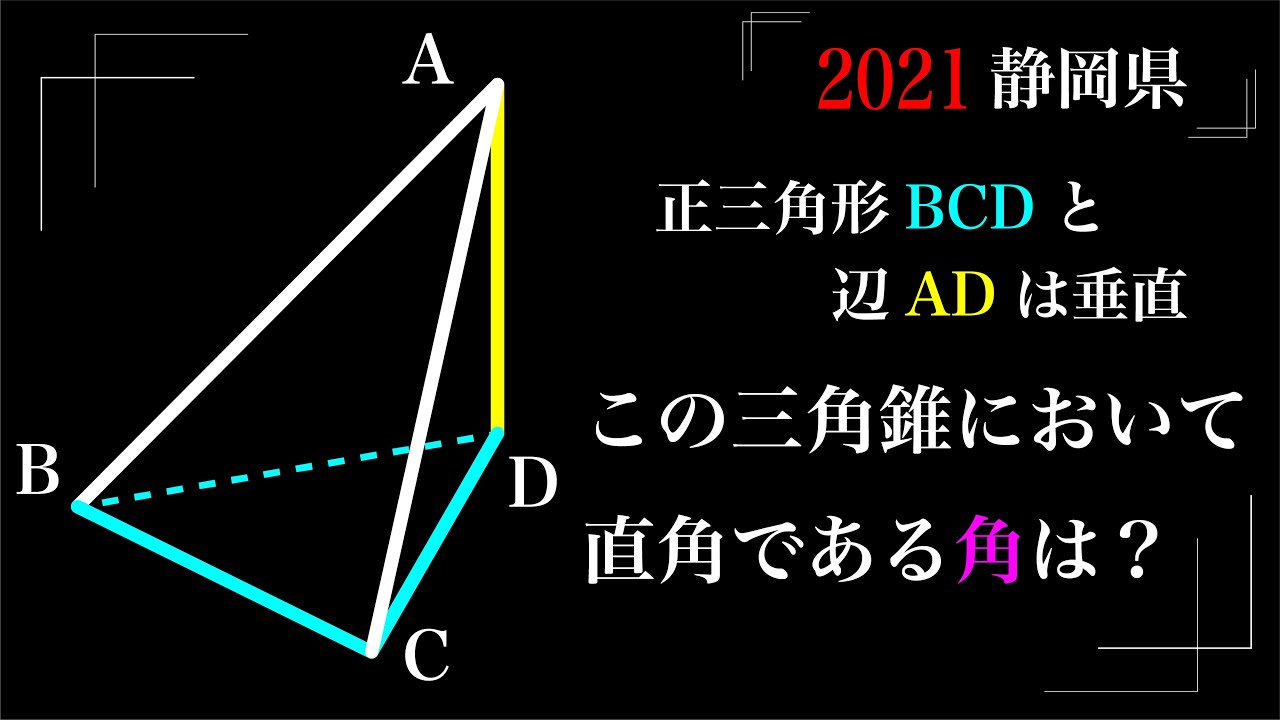
$AD⊥△BCD$
直角である角は?
*図は動画内参照
2021静岡県
この動画を見る
$AD⊥△BCD$
直角である角は?
*図は動画内参照
2021静岡県
【理数個別の過去問解説】1978年度東京工業大学 数学 第2問解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,cは1<a<b<cをみたす整数とし,(ab-1)(bc-1)(ca-1)はabcで割り切れるとする。このとき次の問に答えよう。
(1)ab+bc+ca-1はabcで割り切れることを示そう。
(2)a,b,cをすべて求めよう。
この動画を見る
a,b,cは1<a<b<cをみたす整数とし,(ab-1)(bc-1)(ca-1)はabcで割り切れるとする。このとき次の問に答えよう。
(1)ab+bc+ca-1はabcで割り切れることを示そう。
(2)a,b,cをすべて求めよう。
福田の数学〜早稲田大学2021年社会科学部第3問〜整式の割り算の余りと整数の余りの割り算の関係

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ $k$を$3$以上の整数とする。k進法で$2021_{k}$と表される整数$N$を考える。次の問いに答えよ。
$(1)N$が$k-1$で割り切れるときの$k$の値を求めよ。
$(2)N$を$k+1$で割ったときの余りを$k$で表せ。
$(3)N$を$k+2$で割ったときの余りが$1$となる$k$を全て求めよ。
2021早稲田大学社会科学部過去問
この動画を見る
${\Large\boxed{3}}$ $k$を$3$以上の整数とする。k進法で$2021_{k}$と表される整数$N$を考える。次の問いに答えよ。
$(1)N$が$k-1$で割り切れるときの$k$の値を求めよ。
$(2)N$を$k+1$で割ったときの余りを$k$で表せ。
$(3)N$を$k+2$で割ったときの余りが$1$となる$k$を全て求めよ。
2021早稲田大学社会科学部過去問
【理数個別の過去問解説】1968年度東京工業大学 数学 第1問解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
不等式$ab+1≦abc≦bc+ca+ab+1$をみたす自然数a,b,cのすべての組を求めよう。ただ し、a>b>cとする。
この動画を見る
不等式$ab+1≦abc≦bc+ca+ab+1$をみたす自然数a,b,cのすべての組を求めよう。ただ し、a>b>cとする。
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^{2x^2-1}+2・3^{(x+1)^2}-5・3^{4(x+1)}=0$
この動画を見る
実数解を求めよ.
$3^{2x^2-1}+2・3^{(x+1)^2}-5・3^{4(x+1)}=0$
