 数A
数A
 数A
数A
17愛知県教員採用試験(数学:1-2番 整数問題)

単元:
#数Ⅰ#数A#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$\frac{n}{225} < 1$ $(n \in \mathbb{N})$をみたす既約分数の個数
この動画を見る
1⃣-(2)
$\frac{n}{225} < 1$ $(n \in \mathbb{N})$をみたす既約分数の個数
17愛知県教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣ $x,y \in \mathbb{N}$
(1)$xy+3x-2y=30$をみたす(x,y)
(2)$x^3-xy-2y+2=0$をみたす(x,y)
この動画を見る
1⃣ $x,y \in \mathbb{N}$
(1)$xy+3x-2y=30$をみたす(x,y)
(2)$x^3-xy-2y+2=0$をみたす(x,y)
【理数個別の過去問解説】2007年度千葉大学 数学 第2問解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは奇数とする。このとき、次のことを証明せよ。
(1)n²-1は8の倍数である。
(2)n⁵-nは3の倍数である。
(3)n⁵-nは120の倍数である。
千葉大学(文理共通)2007年第2問より
この動画を見る
nは奇数とする。このとき、次のことを証明せよ。
(1)n²-1は8の倍数である。
(2)n⁵-nは3の倍数である。
(3)n⁵-nは120の倍数である。
千葉大学(文理共通)2007年第2問より
【高校数学】原因の確率~病原菌の問題~ 2-9【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある病原菌の検査試薬は、病原菌に感染しているのに誤って陰性と判断する確率が
1%, 「感染していないのに誤って陽性と判断する確率が2%である。全体の1%がこの
病原菌に感染している集団から1つの個体を取り出すとき、陽性だったのに、実際
には病原菌に感染していない確率を求めよ。
この動画を見る
ある病原菌の検査試薬は、病原菌に感染しているのに誤って陰性と判断する確率が
1%, 「感染していないのに誤って陽性と判断する確率が2%である。全体の1%がこの
病原菌に感染している集団から1つの個体を取り出すとき、陽性だったのに、実際
には病原菌に感染していない確率を求めよ。
16京都府教員採用試験(数学:5番 整数問題)

単元:
#数Ⅰ#数A#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
5⃣ $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2014}{2015},\frac{2015}{2015}$のうち既約分数の個数を求めよ。
この動画を見る
5⃣ $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2014}{2015},\frac{2015}{2015}$のうち既約分数の個数を求めよ。
【高校数学】原因の確率~不良品の確率など2題~ 2-9【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
ある製品を製造する工場A、Bがあり、Aの製品には3%、Bの製品には4%の不良品が
含まれている。
Aの製品とBの製品を、4:5の割合で混ぜた大量の製品の中から1個を取り出すとき、
次の確率を求めよ。
(a) それが不良品である確率
(b) 不良品であったときに、それがAの製品である確率
-----------------
2⃣
箱Aには白玉4個と赤玉5個、箱Bには白玉3個と赤玉2個と青玉7個が入っている。
まず、任意に1つの箱を選び、次にその箱の中から玉を1個取り出すものとする。
取り出された玉の色が白であったとき、それが箱Bから取り出された確率を求めよ。
この動画を見る
1⃣
ある製品を製造する工場A、Bがあり、Aの製品には3%、Bの製品には4%の不良品が
含まれている。
Aの製品とBの製品を、4:5の割合で混ぜた大量の製品の中から1個を取り出すとき、
次の確率を求めよ。
(a) それが不良品である確率
(b) 不良品であったときに、それがAの製品である確率
-----------------
2⃣
箱Aには白玉4個と赤玉5個、箱Bには白玉3個と赤玉2個と青玉7個が入っている。
まず、任意に1つの箱を選び、次にその箱の中から玉を1個取り出すものとする。
取り出された玉の色が白であったとき、それが箱Bから取り出された確率を求めよ。
自作 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$10^{2020}-1$を$3^5$で割った余りを求めよ.
この動画を見る
$10^{2020}-1$を$3^5$で割った余りを求めよ.
【数A】図形の性質:正八面体とその内接球の半径の出し方とその過程における注意点を解説!

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
正八面体とその内接球の半径の出し方とその過程における注意点を解説!
この動画を見る
正八面体とその内接球の半径の出し方とその過程における注意点を解説!
確率 サクッと出そう

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
コインを2枚投げて2枚とも表なら2点それ以外は1点とする.
9回投げて得点の合計が偶数となる確率を求めよ.
この動画を見る
コインを2枚投げて2枚とも表なら2点それ以外は1点とする.
9回投げて得点の合計が偶数となる確率を求めよ.
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{3n^2-5n+218}{3n-2}$が整数となる自然数$n$を求めよ.
この動画を見る
$\dfrac{3n^2-5n+218}{3n-2}$が整数となる自然数$n$を求めよ.
13東京都教員採用試験(数学:1番 整数問題)
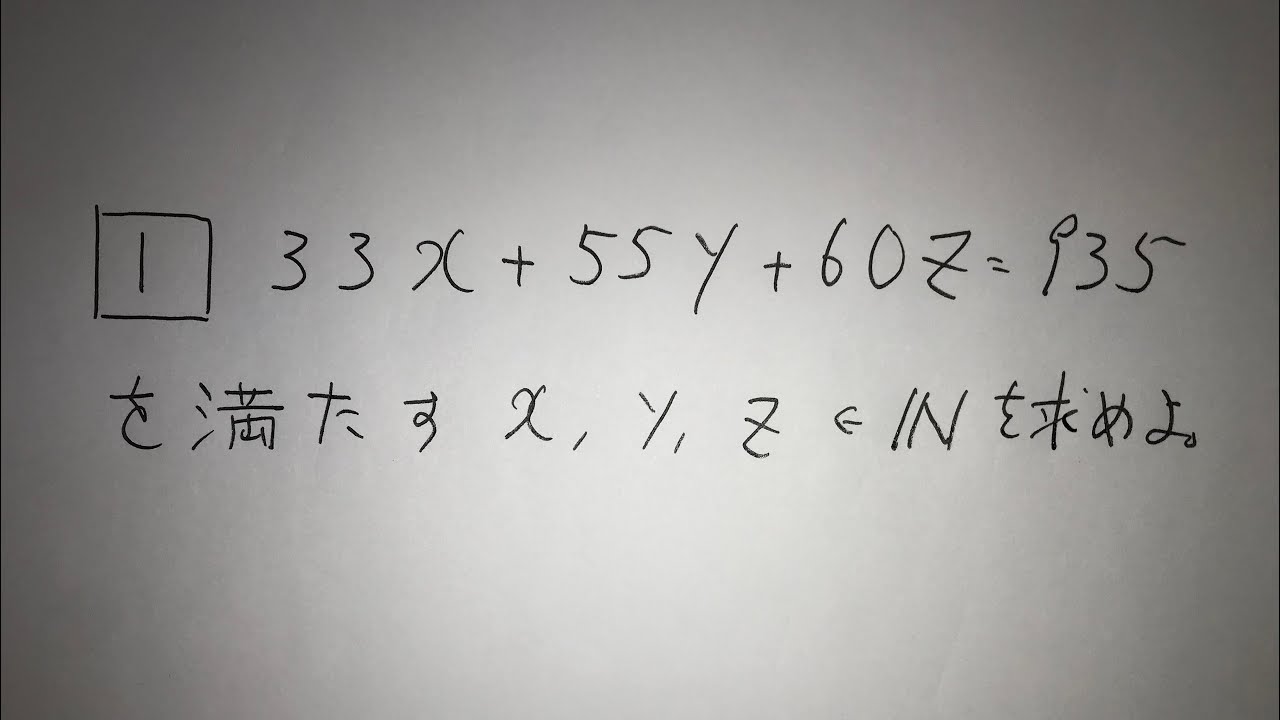
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣ 33x+55y+60z=935を満たす$x,y,z \in \mathbb{ N }$を求めよ。
この動画を見る
1⃣ 33x+55y+60z=935を満たす$x,y,z \in \mathbb{ N }$を求めよ。
京大院生 古賀真輝 フェルマーの小定理を証明する

自作 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^{12}-15n^6+21$が素数となる自然数$n$を求めよ.
この動画を見る
$n^{12}-15n^6+21$が素数となる自然数$n$を求めよ.
14奈良県教員採用試験(数学:2-1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣-(1)
$\sqrt{n^2+211}$が整数となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣-(1)
$\sqrt{n^2+211}$が整数となる$n \in \mathbb{ N }$を求めよ。
15東京都教員採用試験(数学:1-1 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$m^2-mn+3m-3n-7=0$
をみたす自然数の組(m,n)を求めよ。
この動画を見る
1⃣-(1)
$m^2-mn+3m-3n-7=0$
をみたす自然数の組(m,n)を求めよ。
自作 整数問題2
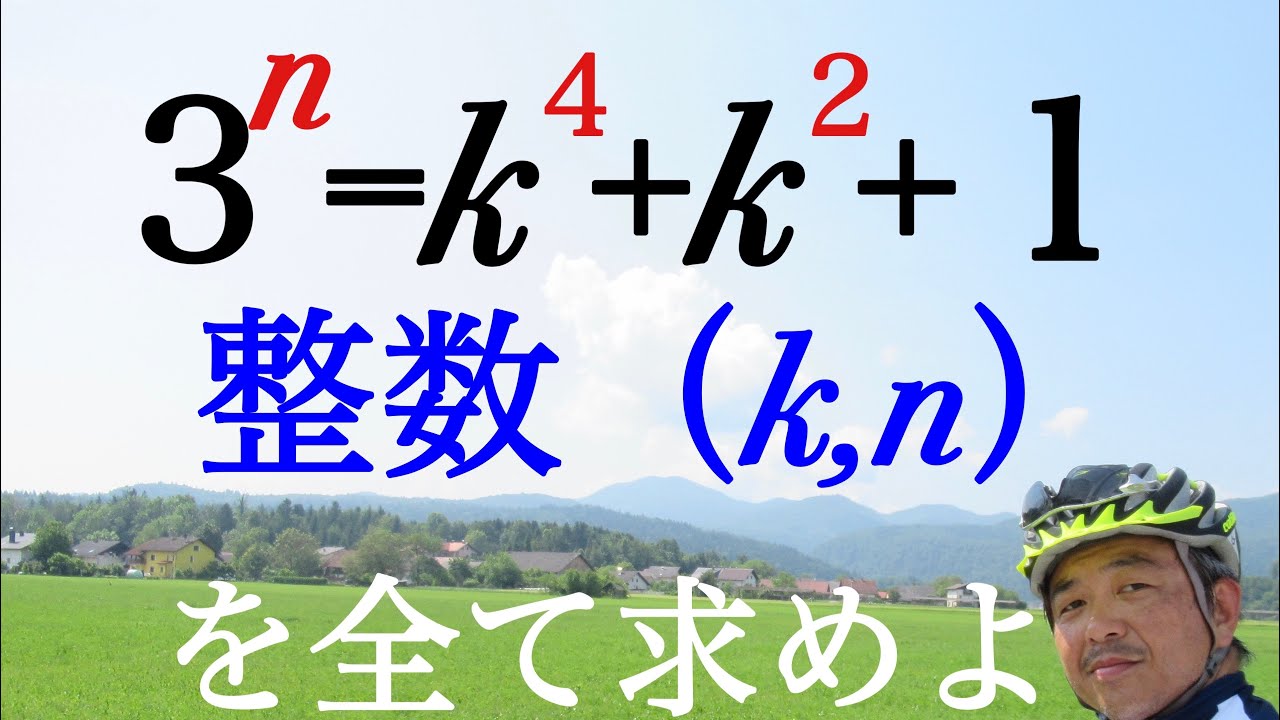
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3^n=k^4+k^2+1$
整数$(k,n)$をすべて求めよ.
この動画を見る
$3^n=k^4+k^2+1$
整数$(k,n)$をすべて求めよ.
自作 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$13^n=k^2+672$
自然数$(k,n)$をすべて求めよ.
この動画を見る
$13^n=k^2+672$
自然数$(k,n)$をすべて求めよ.
【高校数学】条件付き確率例題~組合せを使おう~ 2-8.5【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
袋Aには白玉3個と黒玉5個、袋Bには白玉2個と黒玉2個が入っている。
まず、Aから2個を取り出して、Bに入れ、次にBから2個を取り出してAに戻す。
このとき、袋Aの白玉の個数が初めより増加する確率を求めよ。
この動画を見る
袋Aには白玉3個と黒玉5個、袋Bには白玉2個と黒玉2個が入っている。
まず、Aから2個を取り出して、Bに入れ、次にBから2個を取り出してAに戻す。
このとき、袋Aの白玉の個数が初めより増加する確率を求めよ。
13奈良県教員採用試験(数学:1-1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
この動画を見る
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
15奈良県教員採用試験(数学:中-4番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
この動画を見る
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
灘中 難関大学並の整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A=123456789$
$A$の2つの数を入れかえてできる数を小さい順に$a_1,a_2・・・・・・a_{36}$とする.
$a_1=123456798$
$a_{36}=923456781$
$b_k=a_k-A,1\leqq k\leqq 36$である.
(1)$1000$で割り切れる$b_k$の個数を求めよ.
(2)$37$で割り切れる$b_k$の個数を求めよ.
(3)$b_1 \times b_2 \times b_3 \times ・・・\times b_{36}$は3で何回割り切れるか
2016灘中過去問
この動画を見る
$A=123456789$
$A$の2つの数を入れかえてできる数を小さい順に$a_1,a_2・・・・・・a_{36}$とする.
$a_1=123456798$
$a_{36}=923456781$
$b_k=a_k-A,1\leqq k\leqq 36$である.
(1)$1000$で割り切れる$b_k$の個数を求めよ.
(2)$37$で割り切れる$b_k$の個数を求めよ.
(3)$b_1 \times b_2 \times b_3 \times ・・・\times b_{36}$は3で何回割り切れるか
2016灘中過去問
小樽商科大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{2n-2}{n^2+2n+2}$が整数となる整数$n$を求めよ.
2018小樽商科大過去問
この動画を見る
$\dfrac{2n-2}{n^2+2n+2}$が整数となる整数$n$を求めよ.
2018小樽商科大過去問
【高校数学】条件付き確率例題~標準問題解いてこ~ 2-8.5【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
1つのつぼに赤玉と白玉が合計10個入っている。
このつぼから1個の玉を取り出し、それをつぼへ戻さずにまた1個の玉を取り出す。
このとき、取り出される2個の玉がともに赤玉である確率は$\displaystyle \frac{7}{15}$あるという。
このつぼに初め赤玉は何個入っているか。
-----------------
2⃣
20本のくじの中に当たりが5本ある。
このくじから1本ずつ順に、引いたくじはもとに戻さずに2本を引いたら、2本の中に
当たりくじがあることがわかった。
このとき、1本目のくじが当たりくじである確率を求めよ。
この動画を見る
1⃣
1つのつぼに赤玉と白玉が合計10個入っている。
このつぼから1個の玉を取り出し、それをつぼへ戻さずにまた1個の玉を取り出す。
このとき、取り出される2個の玉がともに赤玉である確率は$\displaystyle \frac{7}{15}$あるという。
このつぼに初め赤玉は何個入っているか。
-----------------
2⃣
20本のくじの中に当たりが5本ある。
このくじから1本ずつ順に、引いたくじはもとに戻さずに2本を引いたら、2本の中に
当たりくじがあることがわかった。
このとき、1本目のくじが当たりくじである確率を求めよ。
【高校数学】条件付き確率例題~これはできなヤバイ~ 2-8.5【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
男子46人,女子54人に試験を行ったところ、男子の合格者は30人、
女子の合格者は36人であった。
この100人の中から1人を選ぶとき次の確率を求めよ。
(a) 選んだ1人が女子であったとき、その人が合格している確率
(b) 選んだ1人が不合格者であったとき、その人が男子である確率
-----------------
2⃣
ある試行における事象$A,B$について、$P(A \cap B)=0.4,P(A)=0.8,P(B)=0.5$のとき
$P_{A}(B) P_{B}(A)$を求めよ。
-----------------
3⃣
8本のくじの中に当たりが3本ある。引いたくじをもとに戻さないで
A、Bの2人がこの順に1本ずつ引くとき、次の確率を求めよ。
(a) Aが当たり、Bがはずれる確率
(b) 2人とも当たる確率
(c) Bが当たる確率
(d) 1人だけが当たる確率
この動画を見る
1⃣
男子46人,女子54人に試験を行ったところ、男子の合格者は30人、
女子の合格者は36人であった。
この100人の中から1人を選ぶとき次の確率を求めよ。
(a) 選んだ1人が女子であったとき、その人が合格している確率
(b) 選んだ1人が不合格者であったとき、その人が男子である確率
-----------------
2⃣
ある試行における事象$A,B$について、$P(A \cap B)=0.4,P(A)=0.8,P(B)=0.5$のとき
$P_{A}(B) P_{B}(A)$を求めよ。
-----------------
3⃣
8本のくじの中に当たりが3本ある。引いたくじをもとに戻さないで
A、Bの2人がこの順に1本ずつ引くとき、次の確率を求めよ。
(a) Aが当たり、Bがはずれる確率
(b) 2人とも当たる確率
(c) Bが当たる確率
(d) 1人だけが当たる確率
【高校数学】確率の乗法定理~改めて確認しよう~ 2-8【数学A】

単元:
#数A#場合の数と確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
当たりくじを3本含む10本のくじの中から引いたくじをもとに戻さないで、
1本ずつ2回続けてくじを引く。2本とも当たる確率を求めよ。
この動画を見る
当たりくじを3本含む10本のくじの中から引いたくじをもとに戻さないで、
1本ずつ2回続けてくじを引く。2本とも当たる確率を求めよ。
【高校数学】条件付き確率~基本の考えと使い方~ 2-7【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある高校の1年生の男女比は8:7であり、メガネをかけた女子生徒は1年生全体の2 割であるという。
女子生徒の1人を選び出したとき、メガネをかけている確率を求めよ。
選び出された1人の生徒が女子であるという事象をA、メガネをかけているという事象をBとする。
この動画を見る
ある高校の1年生の男女比は8:7であり、メガネをかけた女子生徒は1年生全体の2 割であるという。
女子生徒の1人を選び出したとき、メガネをかけている確率を求めよ。
選び出された1人の生徒が女子であるという事象をA、メガネをかけているという事象をBとする。
信州大2020 指数方程式の解の存在条件

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$9^x-k(3^x+3^{-x})+9^{-x}+\dfrac{k^2}{4}+k-17=0$
が実数解をもつ$k$の範囲を求めよ.
2020信州大過去問
この動画を見る
$9^x-k(3^x+3^{-x})+9^{-x}+\dfrac{k^2}{4}+k-17=0$
が実数解をもつ$k$の範囲を求めよ.
2020信州大過去問
【高校数学】反復試行の確率例題~一緒に解いてもやもや解決~ 2-6.5【数学A】

単元:
#数A#場合の数と確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
白玉3個、赤玉2個が入った袋から玉を1個取り出し、色を調べてから
元に戻すことを5回行うとき、次の確率を求めよ。
(a) 白玉をちょうど3回取り出す確率
(b) 5回目に3度目の赤玉を取り出す確率
(c) 5回目に初めて白玉が出る確率
-----------------
2⃣
数直線上を動く点Pが原点にある。1個のさいころを投げて、偶数の目が
出たら正の方向に1、奇数の目が出たら負の方向に1だけPを動かす。
さいころを8回投げたときのPの座標が2である確率を求めよ。
-----------------
3⃣
AとBがテニスの試合を行うとき、各ゲームでA Bが勝つ確率はそれぞれ
$\displaystyle \frac{2}{3} , \displaystyle \frac{1}{3}$あるとする。
3ゲーム先に勝った方が試合の勝者になるとき、Aが勝者になる確率を求めよ。
この動画を見る
1⃣
白玉3個、赤玉2個が入った袋から玉を1個取り出し、色を調べてから
元に戻すことを5回行うとき、次の確率を求めよ。
(a) 白玉をちょうど3回取り出す確率
(b) 5回目に3度目の赤玉を取り出す確率
(c) 5回目に初めて白玉が出る確率
-----------------
2⃣
数直線上を動く点Pが原点にある。1個のさいころを投げて、偶数の目が
出たら正の方向に1、奇数の目が出たら負の方向に1だけPを動かす。
さいころを8回投げたときのPの座標が2である確率を求めよ。
-----------------
3⃣
AとBがテニスの試合を行うとき、各ゲームでA Bが勝つ確率はそれぞれ
$\displaystyle \frac{2}{3} , \displaystyle \frac{1}{3}$あるとする。
3ゲーム先に勝った方が試合の勝者になるとき、Aが勝者になる確率を求めよ。
16神奈川県教員採用試験(数学:整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
【高校数学】反復試行の確率~今までとの違いとつながり~ 2-6【数学A】

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
白玉2個、赤玉4個が入っている袋から玉を1個取り出し、色を調べてから元に戻す。
この試行を6回続けて行うとき白玉が5回以上出る確率を求めよ。
この動画を見る
白玉2個、赤玉4個が入っている袋から玉を1個取り出し、色を調べてから元に戻す。
この試行を6回続けて行うとき白玉が5回以上出る確率を求めよ。
