 式と証明
式と証明
 式と証明
式と証明
【高校数学】二項定理が完璧になる授業~数学苦手必見~ 1-2【数学Ⅱ】

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(x-7y)^7$の展開式における$x^4y^3$の項の係数を求めよ
${}_{ 7 } C_{ 3x^4 }(-2y)^3=-280x^4y^3$
係数:-280
この動画を見る
$(x-7y)^7$の展開式における$x^4y^3$の項の係数を求めよ
${}_{ 7 } C_{ 3x^4 }(-2y)^3=-280x^4y^3$
係数:-280
【超難問】2×2の計算

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅱ#式と証明#整式の除法・分数式・二項定理
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
深読みしすぎた$2 \times 2$の計算
この動画を見る
深読みしすぎた$2 \times 2$の計算
ネイピア数eを用いた相加相乗平均の驚愕証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
ネイピア数eを用いた相加相乗平均の驚愕証明に関して解説していきます.
この動画を見る
ネイピア数eを用いた相加相乗平均の驚愕証明に関して解説していきます.
分数の計算 渋谷教育学園幕張高校

単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20} + \frac{1}{30} + \frac{1}{42}
+ \frac{1}{56} + \frac{1}{72}$
渋谷教育学園幕張高等学校
この動画を見る
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20} + \frac{1}{30} + \frac{1}{42}
+ \frac{1}{56} + \frac{1}{72}$
渋谷教育学園幕張高等学校
福田の数学〜九州大学2022年理系第4問〜定積分の定義から性質を証明する

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
定積分について述べた次の文章を読んで、後の問いに答えよ。
区間$a \leqq x \leqq b$で連続な関数f(x)に対して$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$\int_a^bf(x)dx=F(b)-F(a) \ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$ a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、$f(x),g(x),h(x)$は区間$a \leqq x \leqq b$で連続な関数、$k,l$は定数である。
以下、$f(x)$を区間$0 \leqq x \leqq 1$で連続な増加関数とし、
nを自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、はさみうちの原理より$\lim_{n \to \infty}S_n=\int_0^1f(x)dx$が成り立つ。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことを、導関数の定義に従って示せ。
また、この等式と定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と平均値の定理を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学理系過去問
この動画を見る
定積分について述べた次の文章を読んで、後の問いに答えよ。
区間$a \leqq x \leqq b$で連続な関数f(x)に対して$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$\int_a^bf(x)dx=F(b)-F(a) \ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$ a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、$f(x),g(x),h(x)$は区間$a \leqq x \leqq b$で連続な関数、$k,l$は定数である。
以下、$f(x)$を区間$0 \leqq x \leqq 1$で連続な増加関数とし、
nを自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、はさみうちの原理より$\lim_{n \to \infty}S_n=\int_0^1f(x)dx$が成り立つ。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことを、導関数の定義に従って示せ。
また、この等式と定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と平均値の定理を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第2問〜商と余りの関係と極限

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
この動画を見る
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
分数式の計算 千葉工業大
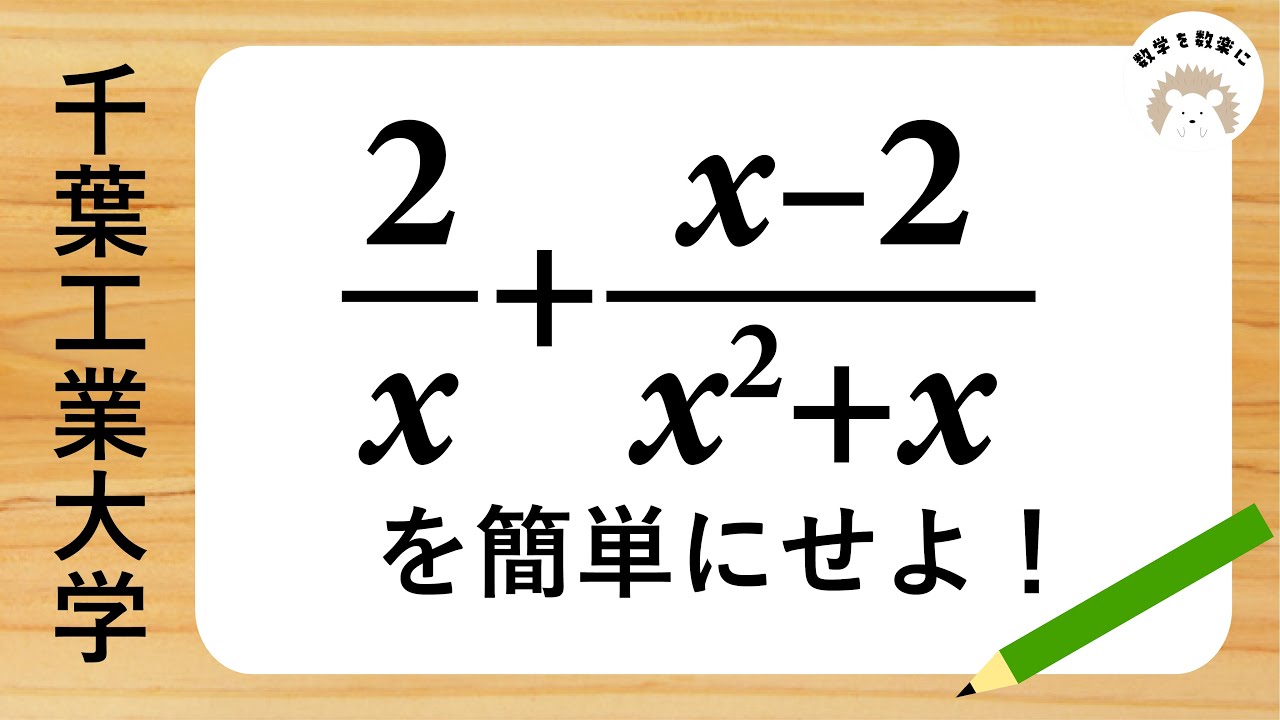
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2}{x} + \frac{x-2}{x^2+x}$を簡単にせよ
千葉工業大学
この動画を見る
$\frac{2}{x} + \frac{x-2}{x^2+x}$を簡単にせよ
千葉工業大学
ゴリゴリ計算【自治医科大学】【数学】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^5+3x^4+px^3+qx-2$が$x^2+3x+4$で割り切れるとき、$p-q$の値を求めよ。
自治医科大過去問
この動画を見る
整式$x^5+3x^4+px^3+qx-2$が$x^2+3x+4$で割り切れるとき、$p-q$の値を求めよ。
自治医科大過去問
福田の数学〜大阪大学2022年文系第3問〜6分の1公式の証明と面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)実数$\alpha,\beta$に対し、
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=\frac{(\alpha-\beta)^3}{6}$
が成り立つことを示せ。
(2)a,bを$b \gt a^2$を満たす定数とし、座標平面に点$A(a,b)$をとる。さらに、
点Aを通り、傾きがkの直線をlとし、直線lと放物線$y=x^2$で囲まれた部分の面積を
$S(k)$とする。kが実数全体を動くとき、$S(k)$の最小値を求めよ。
2022大阪大学文系過去問
この動画を見る
以下の問いに答えよ。
(1)実数$\alpha,\beta$に対し、
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=\frac{(\alpha-\beta)^3}{6}$
が成り立つことを示せ。
(2)a,bを$b \gt a^2$を満たす定数とし、座標平面に点$A(a,b)$をとる。さらに、
点Aを通り、傾きがkの直線をlとし、直線lと放物線$y=x^2$で囲まれた部分の面積を
$S(k)$とする。kが実数全体を動くとき、$S(k)$の最小値を求めよ。
2022大阪大学文系過去問
【上手に文字を置ける?】多項式の割り算の入試問題【流通科学大学】【数学】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$f(x)=x^3+ax^2+bx+c$を$(x+1)^2$で割ると余りが$2x+7$であり、
$x-1$で割ると余りが$17$である。
このときの、$a,b,c$の値は?
流通科学大過去問
この動画を見る
整式$f(x)=x^3+ax^2+bx+c$を$(x+1)^2$で割ると余りが$2x+7$であり、
$x-1$で割ると余りが$17$である。
このときの、$a,b,c$の値は?
流通科学大過去問
中国Jr 数学Olympic あっと驚く解法も

単元:
#数学検定・数学甲子園・数学オリンピック等#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
この動画を見る
$ x^5=1,x \neq 1$とするとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x^8}$の値を求めよ.
中国jr数学オリンピック過去問
【数学Ⅱ/高2の予習】二項定理の基本
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式を求めよ
$(x+3)^4$
この動画を見る
次の式の展開式を求めよ
$(x+3)^4$
二項定理を使ってあることに気付ける?【2017年一橋大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#恒等式・等式・不等式の証明#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
この動画を見る
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
【わかりやすく解説】相加相乗平均の関係を使う不等式の証明②(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a \gt 0,b \gt 0$のとき、不等式$(1+\displaystyle \frac{a}{b})(1+\displaystyle \frac{b}{a}) \geqq 4$が成り立つことを証明せよ
この動画を見る
$a \gt 0,b \gt 0$のとき、不等式$(1+\displaystyle \frac{a}{b})(1+\displaystyle \frac{b}{a}) \geqq 4$が成り立つことを証明せよ
福田の数学〜一橋大学2022年文系第3問〜同値関係の証明と不等式の表す領域

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#図形と方程式#恒等式・等式・不等式の証明#軌跡と領域#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の問いに答えよ。
(1)実数x,yについて、$「|x-y| \leqq x+y」$であることの必要十分条件は
「$x \geqq 0$かつ$y \geqq 0$ 」であることを示せ。
(2)次の不等式で定まるxy平面上の領域を図示せよ。
$|1+y-2x^2-y^2| \leqq 1-y-y^2$
2022一橋大学文系過去問
この動画を見る
次の問いに答えよ。
(1)実数x,yについて、$「|x-y| \leqq x+y」$であることの必要十分条件は
「$x \geqq 0$かつ$y \geqq 0$ 」であることを示せ。
(2)次の不等式で定まるxy平面上の領域を図示せよ。
$|1+y-2x^2-y^2| \leqq 1-y-y^2$
2022一橋大学文系過去問
【わかりやすく解説】相加相乗平均の関係を使う不等式の証明①(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a \gt 0,b \gt 0$のとき、不等式$ab+\displaystyle \frac{4}{ab} \geqq 4$が成り立つことを証明せよ
この動画を見る
$a \gt 0,b \gt 0$のとき、不等式$ab+\displaystyle \frac{4}{ab} \geqq 4$が成り立つことを証明せよ
【次数が高くても焦るな】対称式 入試問題【2017年昭和大学】

単元:
#数Ⅰ#数Ⅱ#数と式#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a+b=1,a^2+b^2=3$のとき、$a^7+b^7$の値を求めよ。
2017昭和大過去問
この動画を見る
$a+b=1,a^2+b^2=3$のとき、$a^7+b^7$の値を求めよ。
2017昭和大過去問
中学生向け「どっちがでかい?」

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$\dfrac{10^{2021}+1}{10^{2022}+1}$ VS $\dfrac{10^{2022}+1}{10^{2023}+1}$
この動画を見る
どちらが大きいか?
$\dfrac{10^{2021}+1}{10^{2022}+1}$ VS $\dfrac{10^{2022}+1}{10^{2023}+1}$
二項定理
基本問題
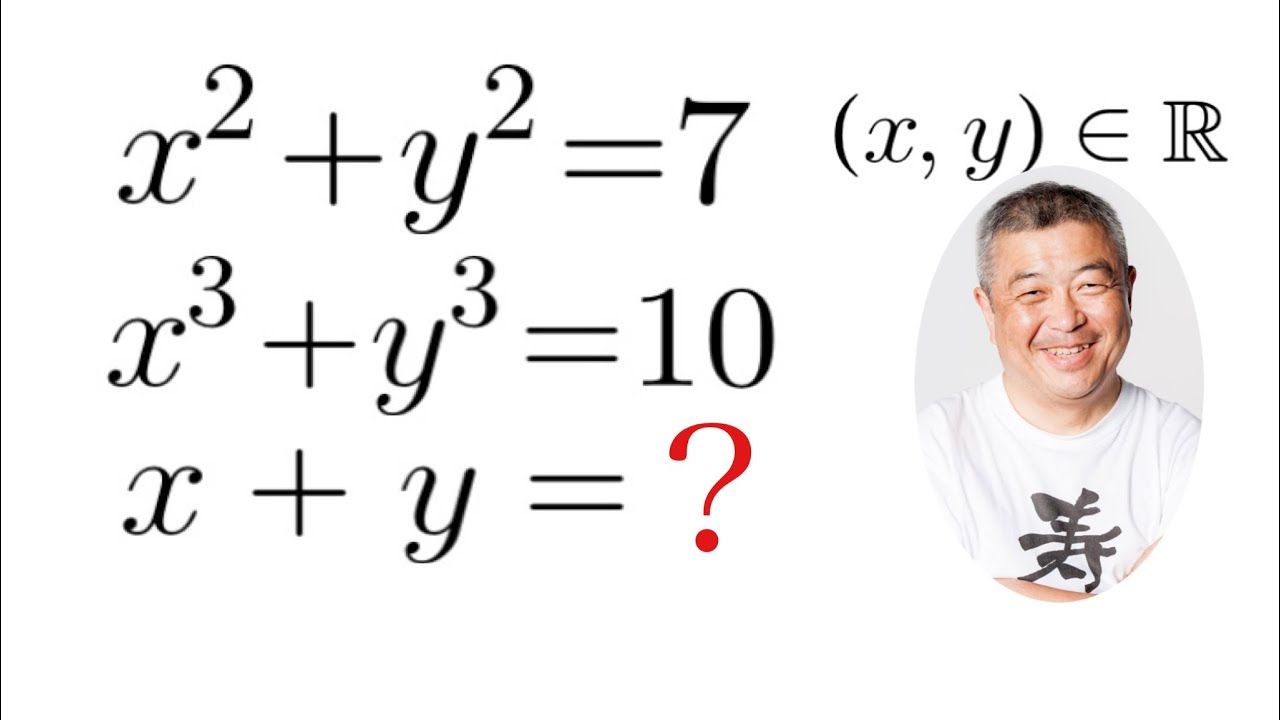
単元:
#数Ⅱ#式と証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yを実数とする.
$ x^2+y^2=7 $
$ x^3+y^3=10 $である.
x+yはいくつであるか求めよ.
この動画を見る
x,yを実数とする.
$ x^2+y^2=7 $
$ x^3+y^3=10 $である.
x+yはいくつであるか求めよ.
【数学Ⅱ】繁分数式(分数の中に分数がある)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を簡単にせよ。
(1)$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
(1)$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
ハルハル様の作成問題 手筋連発

単元:
#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
この動画を見る
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
【わかりやすく】不等式の証明を解説(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不等式を証明せよ。
また、(2)で等号が成り立つのはどのようなときか。
(1)$x \gt 2,y \gt 3$のとき、$xy+6 \gt 3x+2y$
(2)$x^2+5y^2 \geqq 4xy$
この動画を見る
次の不等式を証明せよ。
また、(2)で等号が成り立つのはどのようなときか。
(1)$x \gt 2,y \gt 3$のとき、$xy+6 \gt 3x+2y$
(2)$x^2+5y^2 \geqq 4xy$
大学入試問題#158 名古屋市立大学(2020) 2項展開の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。
出典:2020年名古屋市立大学 入試問題
この動画を見る
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。
出典:2020年名古屋市立大学 入試問題
【わかりやすく】等式の証明(数学Ⅱ/等式の証明)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の等式を証明せよ。
(1)$4ab=(a+b)^2-(a-b)^2$
(2)$(a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2$
この動画を見る
次の等式を証明せよ。
(1)$4ab=(a+b)^2-(a-b)^2$
(2)$(a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2$
【数学Ⅱ/高2の予習】恒等式

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式が$x$についての恒等式となるように、定数$a,b,c$の値を求めよ。
(1)
$3x^2+8x+6=a(x+1)^2+b(x+1)+c$
(2)
$\displaystyle \frac{3}{(x-1)(2x+1)}=\displaystyle \frac{a}{x-1}+\displaystyle \frac{b}{2x-1}$
この動画を見る
次の式が$x$についての恒等式となるように、定数$a,b,c$の値を求めよ。
(1)
$3x^2+8x+6=a(x+1)^2+b(x+1)+c$
(2)
$\displaystyle \frac{3}{(x-1)(2x+1)}=\displaystyle \frac{a}{x-1}+\displaystyle \frac{b}{2x-1}$
整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を$(x+1)(x^2+1)(x^4+1)(x^8+1)$で割った余りを求めよ.
この動画を見る
$x^{2022}$を$(x+1)(x^2+1)(x^4+1)(x^8+1)$で割った余りを求めよ.
【丁寧に解説】テストによく出る繁分数式(分数の中に分数)を解説!
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
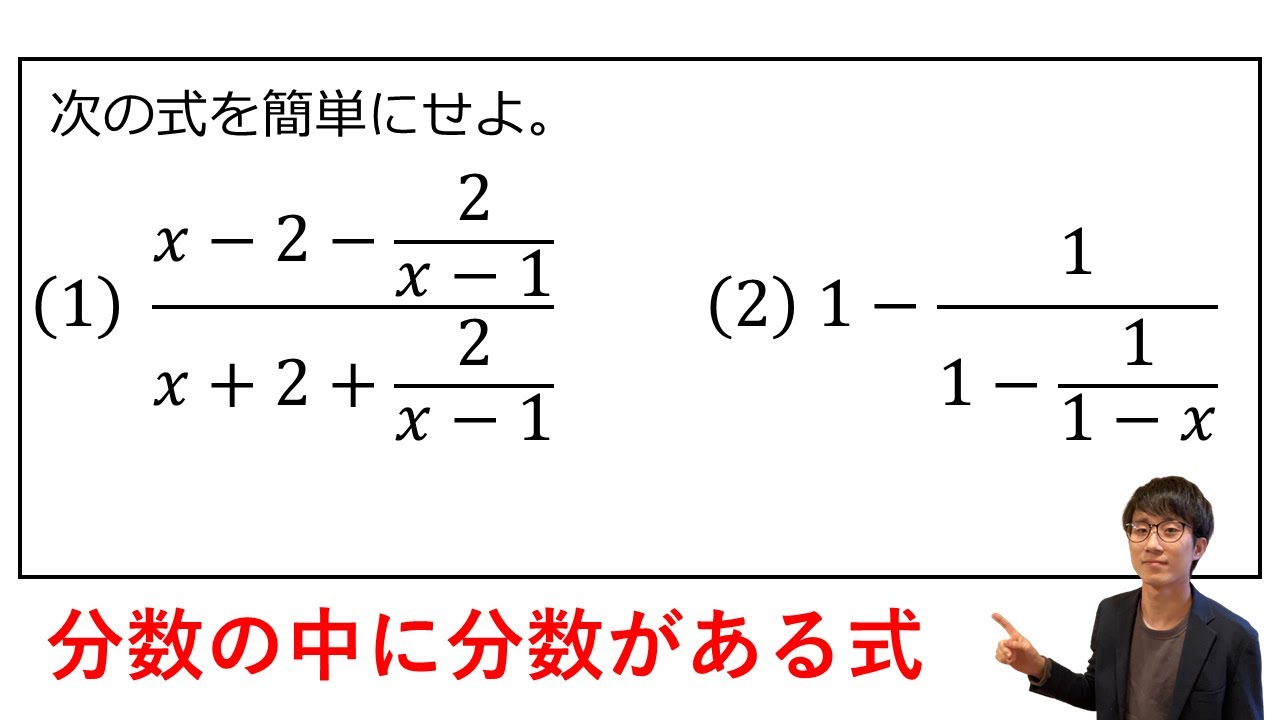
問題文全文(内容文):
次の式を簡単にせよ。
(1)
$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
(1)
$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
【ゼロからわかる】整式の割り算②(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の問いに答えよ。
(1)
$x^2-6x+3$で割ると、商が$2x-3,$余りが$3x$である整数$A$を求めよ。
(2)
$x^3+3x^2+2x+1$を$B$で割ると、商が$x+1,$余りが$x+2$になる。
整数$B$を求めよ。
この動画を見る
次の問いに答えよ。
(1)
$x^2-6x+3$で割ると、商が$2x-3,$余りが$3x$である整数$A$を求めよ。
(2)
$x^3+3x^2+2x+1$を$B$で割ると、商が$x+1,$余りが$x+2$になる。
整数$B$を求めよ。
整式の剰余2022

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^{2022}$を$ x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
この動画を見る
$ x^{2022}$を$ x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
