剰余の定理・因数定理・組み立て除法と高次方程式
剰余の定理・因数定理・組み立て除法と高次方程式
関西学院大 3次方程式の解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022関西学院大学過去問題
a実数
$x^3-(2a+1)x^2-3(a-1)x-a+5 = 0$
①aの値に関わらずx=□は解である
②異なる3つの負の解をもつaの範囲
③$x^3=1$の虚数解の1つをωとする
ω+k(k>0)が解であるならa=□
この動画を見る
2022関西学院大学過去問題
a実数
$x^3-(2a+1)x^2-3(a-1)x-a+5 = 0$
①aの値に関わらずx=□は解である
②異なる3つの負の解をもつaの範囲
③$x^3=1$の虚数解の1つをωとする
ω+k(k>0)が解であるならa=□
同志社大 三次方程式の基本問題
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#同志社大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
同志社大学過去問題
3次方程式
$2x^3+3x^2-12x-6m=0$
は相異なる3つの実数解
$\alpha,\beta,γ(\alpha\lt\beta\lt γ)$をもつ
①$m$の範囲
②$γ$の範囲
この動画を見る
同志社大学過去問題
3次方程式
$2x^3+3x^2-12x-6m=0$
は相異なる3つの実数解
$\alpha,\beta,γ(\alpha\lt\beta\lt γ)$をもつ
①$m$の範囲
②$γ$の範囲
福田の数学〜名古屋大学2023年理系第３問〜方程式の負の実数解の個数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#数学(高校生)#名古屋大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ (1)方程式$e^x$=$\frac{2x^3}{x-1}$ の負の実数解の個数を求めよ。
(2)$y$=$x(x^2-3)$と$y$=$e^x$のグラフの$x$＜0における共有点の個数を求めよ。
(3)$a$を正の実数とし、関数$f(x)$=$x(x^2-a)$を考える。$y$=$f(x)$と$y$=$e^x$のグラフの$x$＜0における共有点は1個のみであるとする。このような$a$がただ1つ存在することを示せ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{3}$ (1)方程式$e^x$=$\frac{2x^3}{x-1}$ の負の実数解の個数を求めよ。
(2)$y$=$x(x^2-3)$と$y$=$e^x$のグラフの$x$＜0における共有点の個数を求めよ。
(3)$a$を正の実数とし、関数$f(x)$=$x(x^2-a)$を考える。$y$=$f(x)$と$y$=$e^x$のグラフの$x$＜0における共有点は1個のみであるとする。このような$a$がただ1つ存在することを示せ。
2023名古屋大学理系過去問
福田の数学〜名古屋大学2023年理系第１問〜4次方程式の解と共役な複素数の性質
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#名古屋大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
大学入試問題#542「どこでも対称性が流行」 九州大学(2023) #高次方程式
単元：
#数Ⅱ#大学入試過去問(数学)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
ますただ
問題文全文(内容文)：
$x^4-2x+3x^2-2x+1=0$を解け
出典：2023年九州大学 入試問題
この動画を見る
$x^4-2x+3x^2-2x+1=0$を解け
出典：2023年九州大学 入試問題
ざ・整式の剰余 様々な解法
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
整式$P(x)$を$(x-2)^2$で割るとあまりは$6x-1$であり,
$(x+1)$で割るとあまりは2である.
$P(x)$を$(x-2)^2(x+1)$で割ったあまりはいくつか？求めよ.
この動画を見る
整式$P(x)$を$(x-2)^2$で割るとあまりは$6x-1$であり,
$(x+1)$で割るとあまりは2である.
$P(x)$を$(x-2)^2(x+1)$で割ったあまりはいくつか？求めよ.
４次方程式の解と係数の関係？
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
この動画を見る
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
埼玉大 直方体の最大値
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#埼玉大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
三辺の和が9cmで表面積が$48m^2$の直方体の体積の最大値を求めよ.
長崎大過去問
この動画を見る
三辺の和が9cmで表面積が$48m^2$の直方体の体積の最大値を求めよ.
長崎大過去問
福田の数学〜慶應義塾大学2023年看護医療学部第１問(4)〜対数方程式
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (4)($\log_29$)($\log_3x$)-$\log_25$=2 を解くとx=$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (4)($\log_29$)($\log_3x$)-$\log_25$=2 を解くとx=$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
整数問題が苦手な人は要チェック！絶対に取りたい整数問題【関西医科大学】【数学 入試問題】
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
( 1) (a + 1)(a - 1)(b + 1)(b - 1) - 4ab を因数分解せよ。
( 2) (a + 1)(a - 1)(b + 1)(b - 1) = 4ab を満たす整数a,bの組で、 a < b の条件を満たすものは
？組あり、そのなかでa,bのどちらも正の整数となる組(a,b) は ？である 。
(2023年 関西医科大学)
この動画を見る
( 1) (a + 1)(a - 1)(b + 1)(b - 1) - 4ab を因数分解せよ。
( 2) (a + 1)(a - 1)(b + 1)(b - 1) = 4ab を満たす整数a,bの組で、 a < b の条件を満たすものは
？組あり、そのなかでa,bのどちらも正の整数となる組(a,b) は ？である 。
(2023年 関西医科大学)
高校入試だけど4次方程式 久留米大附設
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$(x^2-1)^2 = 2x^2 -2$
久留米大付設高等学校（改）
この動画を見る
方程式を解け
$(x^2-1)^2 = 2x^2 -2$
久留米大付設高等学校（改）
神戸大 ３次方程式の基本問題
単元：
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式（不等式・絶対値のある方程式・不等式）#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
この動画を見る
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
ナイスな指数方程式
単元：
#数Ⅱ#式と証明#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を(x,y)としたとき、
$16^{x^2+y}+16^{x+y^2}=1$を求めよ.
この動画を見る
実数解を(x,y)としたとき、
$16^{x^2+y}+16^{x+y^2}=1$を求めよ.
福田の数学〜北海道大学2023年文系第１問〜関数方程式と剰余定理因数定理
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ P(x)をxについての整式とし、P(x)P(-x)=P($x^2$)はxについての恒等式であるとする。
(1)P(0)=0またはP(0)=1 であることを示せ。
(2)P(x)がx-1で割り切れないならば、P(x)-1はx+1で割り切れることを示せ。
(3)次数が2であるP(x)を全て求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{5}$ P(x)をxについての整式とし、P(x)P(-x)=P($x^2$)はxについての恒等式であるとする。
(1)P(0)=0またはP(0)=1 であることを示せ。
(2)P(x)がx-1で割り切れないならば、P(x)-1はx+1で割り切れることを示せ。
(3)次数が2であるP(x)を全て求めよ。
2023北海道大学文系過去問
綺麗な三次方程式
単元：
#数Ⅱ#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(x-3)^3+(x-2)^3+(x-1)^3=x^3$
これを解け.
この動画を見る
$(x-3)^3+(x-2)^3+(x-1)^3=x^3$
これを解け.
福田の数学〜京都大学2023年理系第２問〜空間の位置ベクトルと直線のベクトル方程式
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#空間ベクトル#剰余の定理・因数定理・組み立て除法と高次方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1：2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR：RDを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1：2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR：RDを求めよ。
2023京都大学理系過去問
2023年京大数学！整式の割り算！２通りで解説します【京都大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
この動画を見る
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
福田の数学〜東京大学2023年理系第５問〜整式の割り算と２重因子をもつ条件
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ 整式f(x)=$(x-1)^2(x-2)$を考える。
(1)g(x)を実数を係数とする整式とし、g(x)をf(x)で割った余りをr(x)とおく。
$g(x)^7$をf(x)で割った余りと$r(x)^7$をf(x)で割った余りが等しいことを示せ。
(2)a,bを実数とし、h(x)=$x^2$+ax+b とおく。$h(x)^7$をf(x)で割った余りを$h_1(x)$とおき、$h_1(x)^7$をf(x)で割った余りを$h_2(x)$とおく。$h_2(x)$がh(x)に等しくなるようなa,bの組を全て求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{5}$ 整式f(x)=$(x-1)^2(x-2)$を考える。
(1)g(x)を実数を係数とする整式とし、g(x)をf(x)で割った余りをr(x)とおく。
$g(x)^7$をf(x)で割った余りと$r(x)^7$をf(x)で割った余りが等しいことを示せ。
(2)a,bを実数とし、h(x)=$x^2$+ax+b とおく。$h(x)^7$をf(x)で割った余りを$h_1(x)$とおき、$h_1(x)^7$をf(x)で割った余りを$h_2(x)$とおく。$h_2(x)$がh(x)に等しくなるようなa,bの組を全て求めよ。
2023東京大学理系過去問
【高校数学】むやみに代入するな！因数定理のちょっとした裏技！ #Shorts
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
因数分解せよ。
$x^3+6x^2-6x+7$
この動画を見る
因数分解せよ。
$x^3+6x^2-6x+7$
秋田大（医） 整式の剰余
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$を自然数とし,A,Bを整数とする.
$x^{2n}-4x^8+Ax+B$が$x^2-x+1$で割り切れるA,Bの値を求めよ.
秋田大(医)過去問
この動画を見る
$n$を自然数とし,A,Bを整数とする.
$x^{2n}-4x^8+Ax+B$が$x^2-x+1$で割り切れるA,Bの値を求めよ.
秋田大(医)過去問
福田の1.5倍速演習〜合格する重要問題098〜早稲田大学2020年度商学部第１問(1)〜積分方程式
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (1)m, nを正の整数とする。n次関数f(x)が、次の等式を満たしているとき、f(x)=$\boxed{\ \ ア\ \ }$である。
$\displaystyle\int_0^x(x-t)^{m-1}f(t)dt$=$\left\{f(x)\right\}^m$
2020早稲田大学商学部過去問
この動画を見る
$\Large\boxed{1}$ (1)m, nを正の整数とする。n次関数f(x)が、次の等式を満たしているとき、f(x)=$\boxed{\ \ ア\ \ }$である。
$\displaystyle\int_0^x(x-t)^{m-1}f(t)dt$=$\left\{f(x)\right\}^m$
2020早稲田大学商学部過去問
福田の数学〜北里大学2020年医学部第１問(1)〜虚数係数の３次方程式の解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ (1)$p,q$を実数の定数、$i$を虚数単位とする。$x$の方程式
$x^3-(p-i)x^2+(q-pi)x-2p+\displaystyle\frac{3p}{2}i=0$
が$2+i$を解にもつとする。このとき、$p=\boxed{\ \ ア\ \ }$,$q=\boxed{\ \ イ\ \ }$である。また、この方程式の$2+i$以外の解を$\alpha$,$\beta$(ただし、|$\alpha$| $\lt$ |$\beta$|)とおくと$\left(\displaystyle\frac{\beta-i}{\alpha}\right)^7=\boxed{\ \ ウ \ \ }$である。
2020北里大学医学部過去問
この動画を見る
$\Large{\boxed{1}}$ (1)$p,q$を実数の定数、$i$を虚数単位とする。$x$の方程式
$x^3-(p-i)x^2+(q-pi)x-2p+\displaystyle\frac{3p}{2}i=0$
が$2+i$を解にもつとする。このとき、$p=\boxed{\ \ ア\ \ }$,$q=\boxed{\ \ イ\ \ }$である。また、この方程式の$2+i$以外の解を$\alpha$,$\beta$(ただし、|$\alpha$| $\lt$ |$\beta$|)とおくと$\left(\displaystyle\frac{\beta-i}{\alpha}\right)^7=\boxed{\ \ ウ \ \ }$である。
2020北里大学医学部過去問
福田の1.5倍速演習〜合格する重要問題033〜浜松医科大学2016年度理系第３問〜指数方程式の解の個数
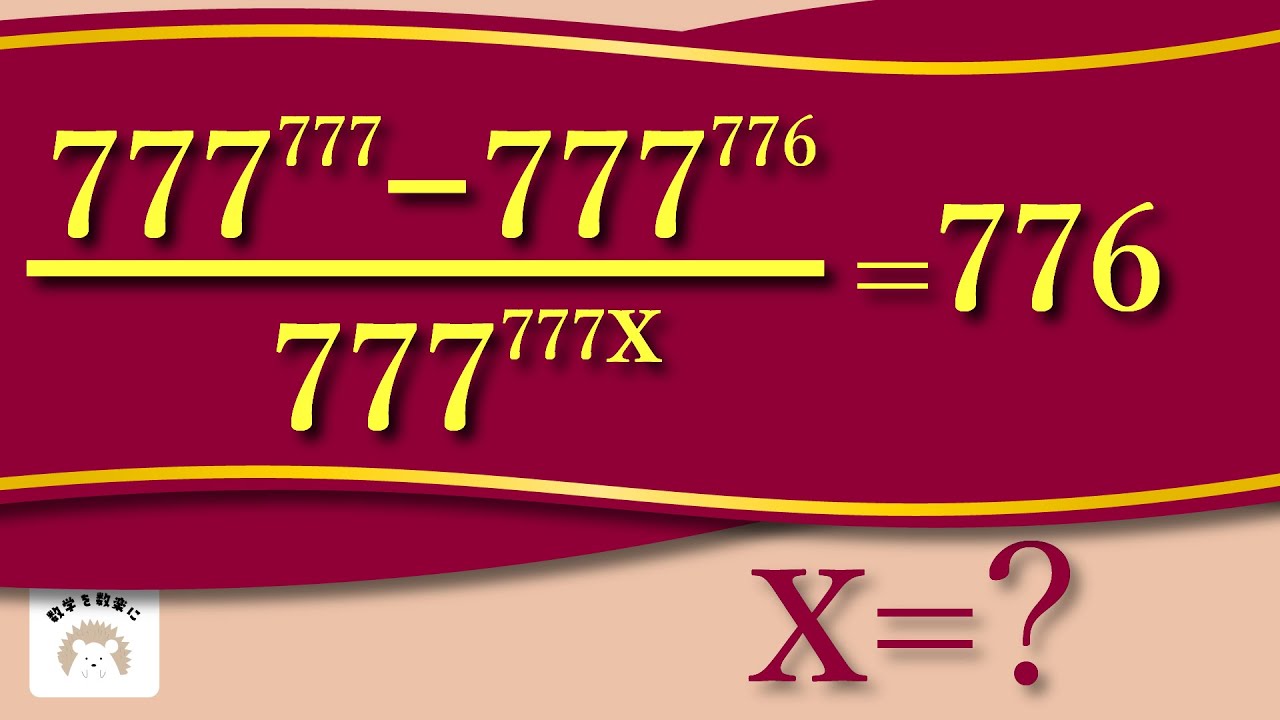
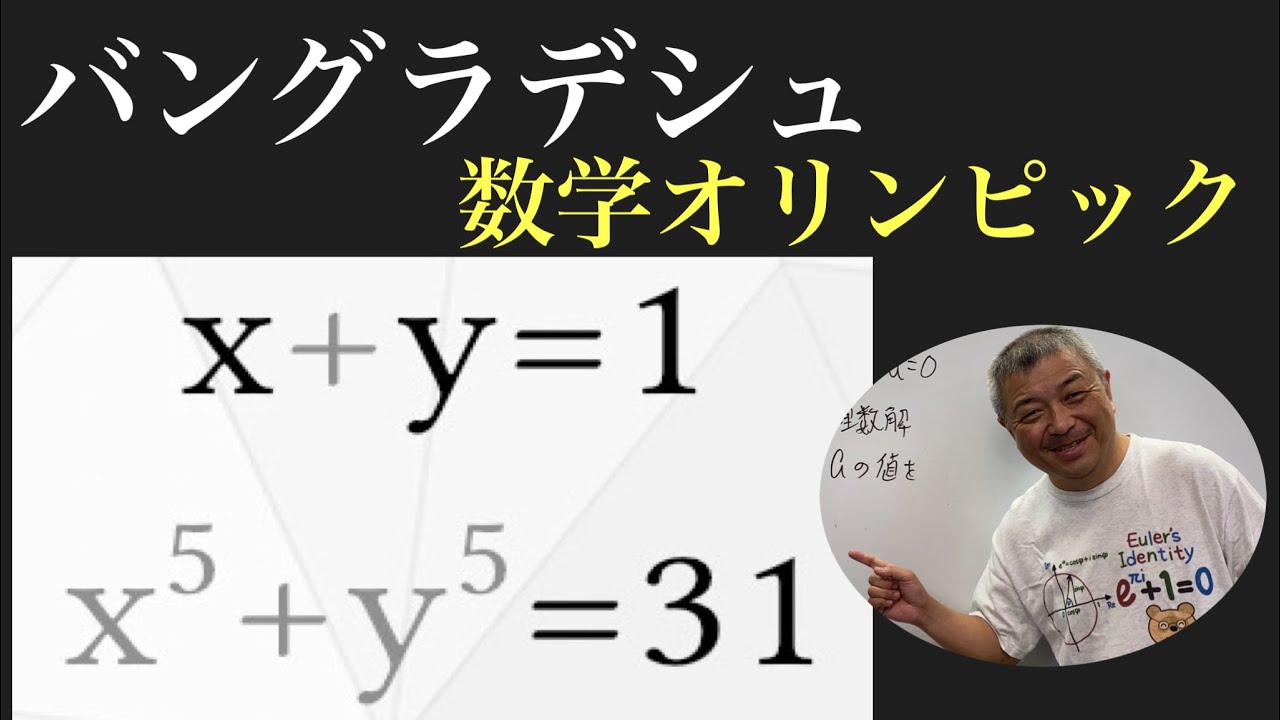
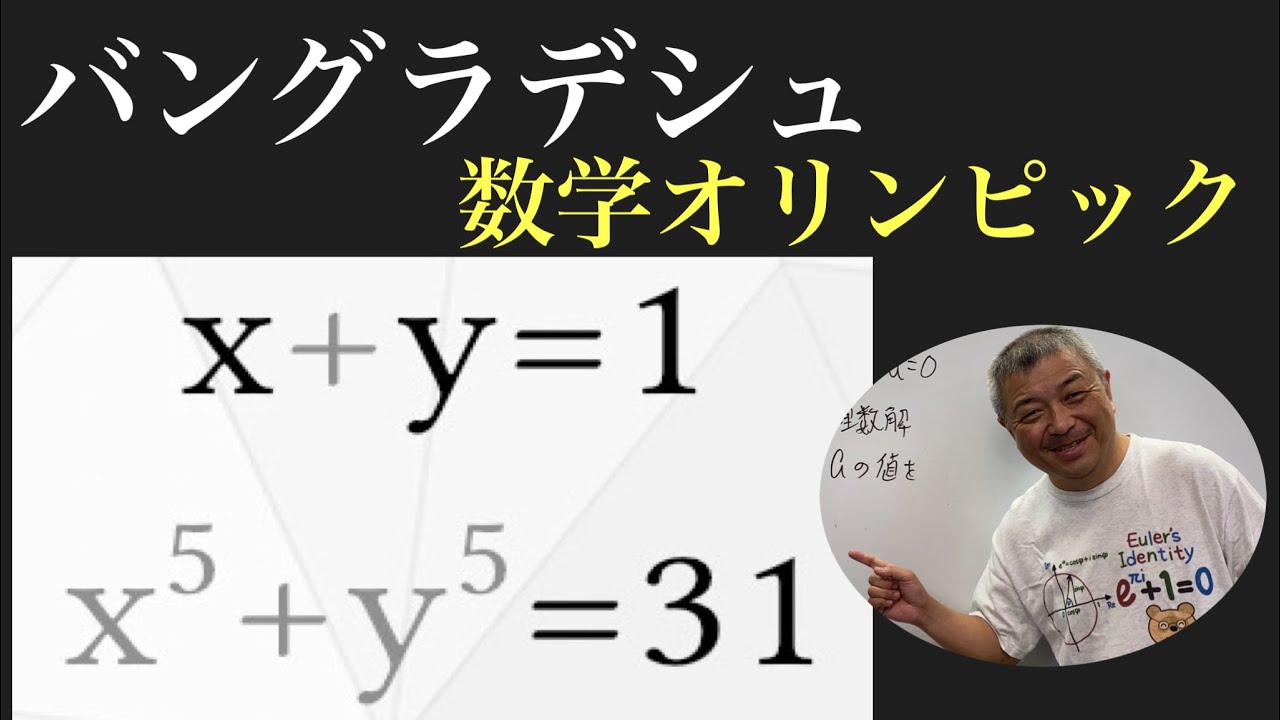
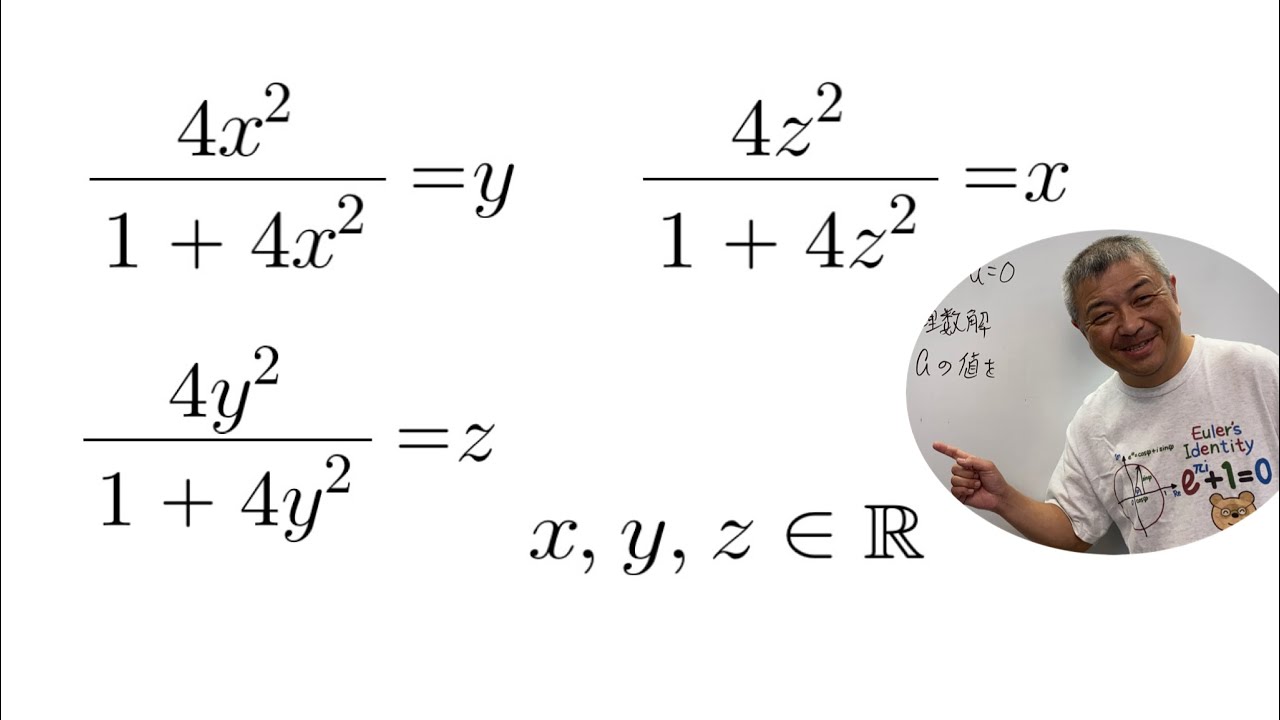
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
以下の問いに答えよ。なお、必要があれば以下の極限値の公式を用いてもよい。
$\lim_{x \to \infty}\frac{x}{e^x}=0$
(1)方程式$2^x=x^2 (x \gt 0)$の実数解の個数を求めよ。
(2)aを正の実数とし、xについての方程式$a^x=x^a (x \gt 0)$を考える。
$(\textrm{a})$方程式$a^x=x^a (x \gt 0)$の実数解の個数を求めよ。
$(\textrm{b})$方程式$a^x=x^a (x \gt 0)$でa,xがともに正の整数となるa,xの組$(a,x)$
をすべて求めよ。ただし$a \ne x$とする。
2016浜松医科大学理系過去問
この動画を見る
以下の問いに答えよ。なお、必要があれば以下の極限値の公式を用いてもよい。
$\lim_{x \to \infty}\frac{x}{e^x}=0$
(1)方程式$2^x=x^2 (x \gt 0)$の実数解の個数を求めよ。
(2)aを正の実数とし、xについての方程式$a^x=x^a (x \gt 0)$を考える。
$(\textrm{a})$方程式$a^x=x^a (x \gt 0)$の実数解の個数を求めよ。
$(\textrm{b})$方程式$a^x=x^a (x \gt 0)$でa,xがともに正の整数となるa,xの組$(a,x)$
をすべて求めよ。ただし$a \ne x$とする。
2016浜松医科大学理系過去問
福田の1.5倍速演習〜合格する重要問題026〜神戸大学2016年度理系数学第５問〜極方程式と媒介変数表示
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#平面上の曲線#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
極方程式で表されたxy平面上の曲線$r=1+\cos\theta(0 \leqq \theta \leqq 2\pi)$をCとする。
(1)曲線C上の点を直交座標(x,y)で表したとき、$\frac{dx}{d\theta}=0$となる点、および
$\frac{dy}{d\theta}=0$となる点の直交座標を求めよ。
(2)$\lim_{\theta \to \pi}\frac{dy}{dx}$を求めよ。
(3)曲線Cの概形をxy平面上にかけ。
(4)曲線Cの長さを求めよ。
2016神戸大学理系過去問
この動画を見る
極方程式で表されたxy平面上の曲線$r=1+\cos\theta(0 \leqq \theta \leqq 2\pi)$をCとする。
(1)曲線C上の点を直交座標(x,y)で表したとき、$\frac{dx}{d\theta}=0$となる点、および
$\frac{dy}{d\theta}=0$となる点の直交座標を求めよ。
(2)$\lim_{\theta \to \pi}\frac{dy}{dx}$を求めよ。
(3)曲線Cの概形をxy平面上にかけ。
(4)曲線Cの長さを求めよ。
2016神戸大学理系過去問
福田の1.5倍速演習〜合格する重要問題010〜千葉大学2015年度理系数学第６問〜論証と剰余類
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
この動画を見る
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
福田の数学〜中央大学2022年理工学部第４問〜複素数平面上の共線条件と正三角形になる条件
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$t$を実数とし、xの3次式f(x) を
$f(x) = x^3 + (1-2t)x^2+(4-2t)x+4$
により定める。以下の問いに答えよ。
(1) 3次式f(x) を実数係数の2次式と1次式の積に因数分解し、$f(x) = 0$ が虚数の
解をもつようなtの範囲を求めよ。
実数tが (1) で求めた範囲にあるとき、方程式 $f(x) = 0$ の異なる2つの虚数解を
α, βとし、実数解をγとする。ただし、$α$の虚部は正、$β$の虚部は負とする。
以下、$α, β, γ$を複素数平面上の点とみなす。
(2) $α, β, γ$をtを用いて表せ。また、実数tが (1) で求めた範囲を動くとき、点$α$
が描く図形を複素数平面上に図示せよ。
(3) 3点$α, β, γ$が一直線上にあるようなtの値を求めよ。
(4)3点$α, β, γ$が正三角形の頂点となるようなtの値を求めよ。
2022中央大学理工学部過去問
この動画を見る
$t$を実数とし、xの3次式f(x) を
$f(x) = x^3 + (1-2t)x^2+(4-2t)x+4$
により定める。以下の問いに答えよ。
(1) 3次式f(x) を実数係数の2次式と1次式の積に因数分解し、$f(x) = 0$ が虚数の
解をもつようなtの範囲を求めよ。
実数tが (1) で求めた範囲にあるとき、方程式 $f(x) = 0$ の異なる2つの虚数解を
α, βとし、実数解をγとする。ただし、$α$の虚部は正、$β$の虚部は負とする。
以下、$α, β, γ$を複素数平面上の点とみなす。
(2) $α, β, γ$をtを用いて表せ。また、実数tが (1) で求めた範囲を動くとき、点$α$
が描く図形を複素数平面上に図示せよ。
(3) 3点$α, β, γ$が一直線上にあるようなtの値を求めよ。
(4)3点$α, β, γ$が正三角形の頂点となるようなtの値を求めよ。
2022中央大学理工学部過去問
福田の数学〜中央大学2022年理工学部第4問〜複素数平面上の共線条件と正三角形になる条件
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#剰余の定理・因数定理・組み立て除法と高次方程式#図形への応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
中央大学2022年理工学部第4問解説です
tを実数とし、 xの3次式f(x) を
ƒ(x) = x³ + (1 − 2t)x² + (4 − 2t)x +4
により定める。以下の問いに答えよ。
(1) 3 次式f(x) を実数係数の2次式と1次式の積に因数分解し、f(x)=0 が虚数の
解をもつようなtの範囲を求めよ。
実数t が (1) で求めた範囲にあるとき、 方程式 f(x) = 0 の異なる2つの虚数解を
a,βとし、実数解をγとする。ただし、αの虚部は正、βの虚部は負とする。
以下、α, β,γを複素数平面上の点とみなす。
(2) α, β,γをtを用いて表せ。また、実数t が (1) で求めた範囲を動くとき、点α
が描く図形を複素数平面上に図示せよ。
(3) 3点 α, β, γが一直線上にあるようなtの値を求めよ。
(4) 3点 α, β, γが正三角形の頂点となるようなtの値を求めよ。
この動画を見る
中央大学2022年理工学部第4問解説です
tを実数とし、 xの3次式f(x) を
ƒ(x) = x³ + (1 − 2t)x² + (4 − 2t)x +4
により定める。以下の問いに答えよ。
(1) 3 次式f(x) を実数係数の2次式と1次式の積に因数分解し、f(x)=0 が虚数の
解をもつようなtの範囲を求めよ。
実数t が (1) で求めた範囲にあるとき、 方程式 f(x) = 0 の異なる2つの虚数解を
a,βとし、実数解をγとする。ただし、αの虚部は正、βの虚部は負とする。
以下、α, β,γを複素数平面上の点とみなす。
(2) α, β,γをtを用いて表せ。また、実数t が (1) で求めた範囲を動くとき、点α
が描く図形を複素数平面上に図示せよ。
(3) 3点 α, β, γが一直線上にあるようなtの値を求めよ。
(4) 3点 α, β, γが正三角形の頂点となるようなtの値を求めよ。
(x³+x²+x+1)⁷をx²-x+1で割ったあまりを求めよ
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(x^3+x^2+x+1)^7$を$x^2-x+1$で割ったあまりを求めよ.
この動画を見る
$(x^3+x^2+x+1)^7$を$x^2-x+1$で割ったあまりを求めよ.
宮城教育大・多項式の剰余
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$P(x),Q(x)$はxの実数係数多項式である.
$P(x),Q(x)$が$x^2+1$で割り切れるなら$P(x),Q(x)$の少なくとも一方は$x^2+1$で割り切れることを証明せよ.
(1)$P(i)=0$ならば$P(x)$は$x^2+1$で割り切れることを示せ.
宮城教育大過去問
この動画を見る
$P(x),Q(x)$はxの実数係数多項式である.
$P(x),Q(x)$が$x^2+1$で割り切れるなら$P(x),Q(x)$の少なくとも一方は$x^2+1$で割り切れることを証明せよ.
(1)$P(i)=0$ならば$P(x)$は$x^2+1$で割り切れることを示せ.
宮城教育大過去問
福田の数学〜上智大学2022年TEAP文系型第３問〜３次方程式の解の個数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
aを実数の定数として3次関数
$f(x)=9x^3-9x+a$
を考える。
(1) $y=f(x)$のグラフとx軸の共有点が2つ以上あるようなaの範囲は
$\boxed{ネ}\sqrt{\boxed{ノ}}\leqq a \leqq \boxed{ハ}\sqrt{\boxed{ヒ}}$である。
(2)$a= \boxed{ハ}\sqrt{\boxed{ヒ}}$のとき、方程式$f(x)= 0$の最も小さい解は
$\frac{\boxed{フ}}{\boxed{ヘ}}\sqrt{\boxed{ヒ}}$
であり、$y=f(x)$のグラフとx軸の囲む図形の面積は$\frac{\boxed{マ}}{\boxed{ミ}}$である。
2022上智大学文系過去問
この動画を見る
aを実数の定数として3次関数
$f(x)=9x^3-9x+a$
を考える。
(1) $y=f(x)$のグラフとx軸の共有点が2つ以上あるようなaの範囲は
$\boxed{ネ}\sqrt{\boxed{ノ}}\leqq a \leqq \boxed{ハ}\sqrt{\boxed{ヒ}}$である。
(2)$a= \boxed{ハ}\sqrt{\boxed{ヒ}}$のとき、方程式$f(x)= 0$の最も小さい解は
$\frac{\boxed{フ}}{\boxed{ヘ}}\sqrt{\boxed{ヒ}}$
であり、$y=f(x)$のグラフとx軸の囲む図形の面積は$\frac{\boxed{マ}}{\boxed{ミ}}$である。
2022上智大学文系過去問