 剰余の定理・因数定理・組み立て除法と高次方程式
剰余の定理・因数定理・組み立て除法と高次方程式
 剰余の定理・因数定理・組み立て除法と高次方程式
剰余の定理・因数定理・組み立て除法と高次方程式
ガウス記号 剰余

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$\left[\dfrac{4^n}{5}\right]$を$6$で割った余りを求めよ.
この動画を見る
$n$を自然数とする.
$\left[\dfrac{4^n}{5}\right]$を$6$で割った余りを求めよ.
佐賀大(医)3次方程式の解の公式その2
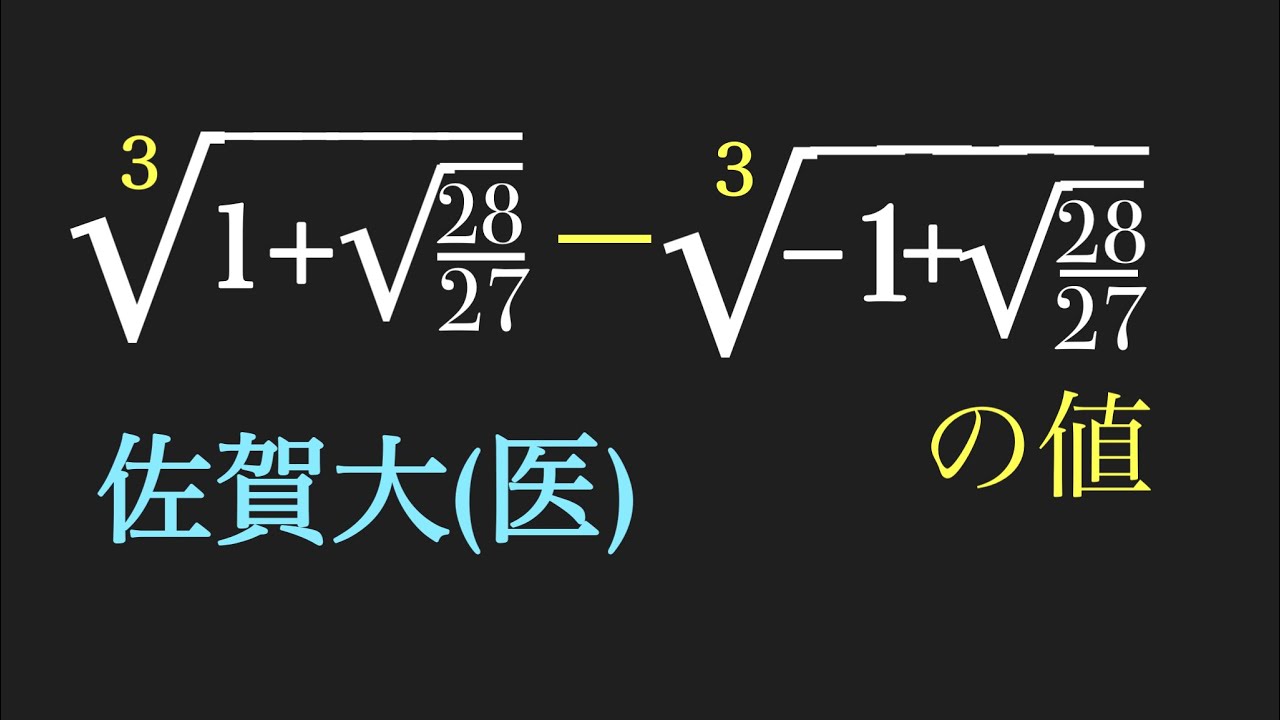
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+px-q=0$
$\alpha-\beta=q,\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は解である.
$\sqrt[3]{1+\sqrt{\dfrac{28}{27}}}-\sqrt[3]{-1+\sqrt{\dfrac{28}{27}}}$の値を求めよ.
佐賀大(医)過去問
この動画を見る
$x^3+px-q=0$
$\alpha-\beta=q,\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は解である.
$\sqrt[3]{1+\sqrt{\dfrac{28}{27}}}-\sqrt[3]{-1+\sqrt{\dfrac{28}{27}}}$の値を求めよ.
佐賀大(医)過去問
佐賀大(医)3次方程式の解の公式
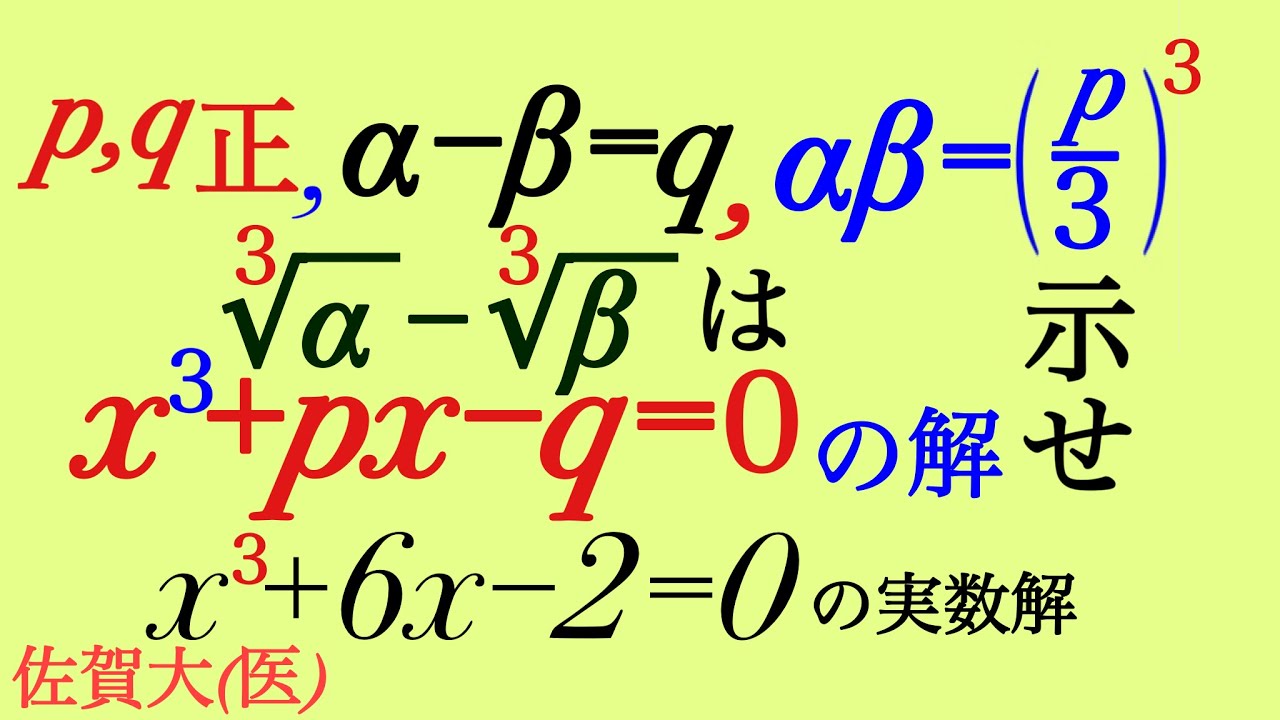
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha,\beta$は正の実数である.
(1)$p,q$正, $\alpha-\beta=q$,$\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は$x^3+px-q=0$の解であることを示せ.
(2)$x^3+6x-2=0$の実数解を求めよ.
2020佐賀大(医)過去問
この動画を見る
$\alpha,\beta$は正の実数である.
(1)$p,q$正, $\alpha-\beta=q$,$\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は$x^3+px-q=0$の解であることを示せ.
(2)$x^3+6x-2=0$の実数解を求めよ.
2020佐賀大(医)過去問
14京都府教員採用試験(数学:4番 3次方程式)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$x^3+(a+4)x^2+(a+2)x-2a-7=0$
が異なる3つの実数解をもつように
定数$a$の値の範囲を求めよ.
この動画を見る
$\boxed{4}$
$x^3+(a+4)x^2+(a+2)x-2a-7=0$
が異なる3つの実数解をもつように
定数$a$の値の範囲を求めよ.
連立3元3次方程式
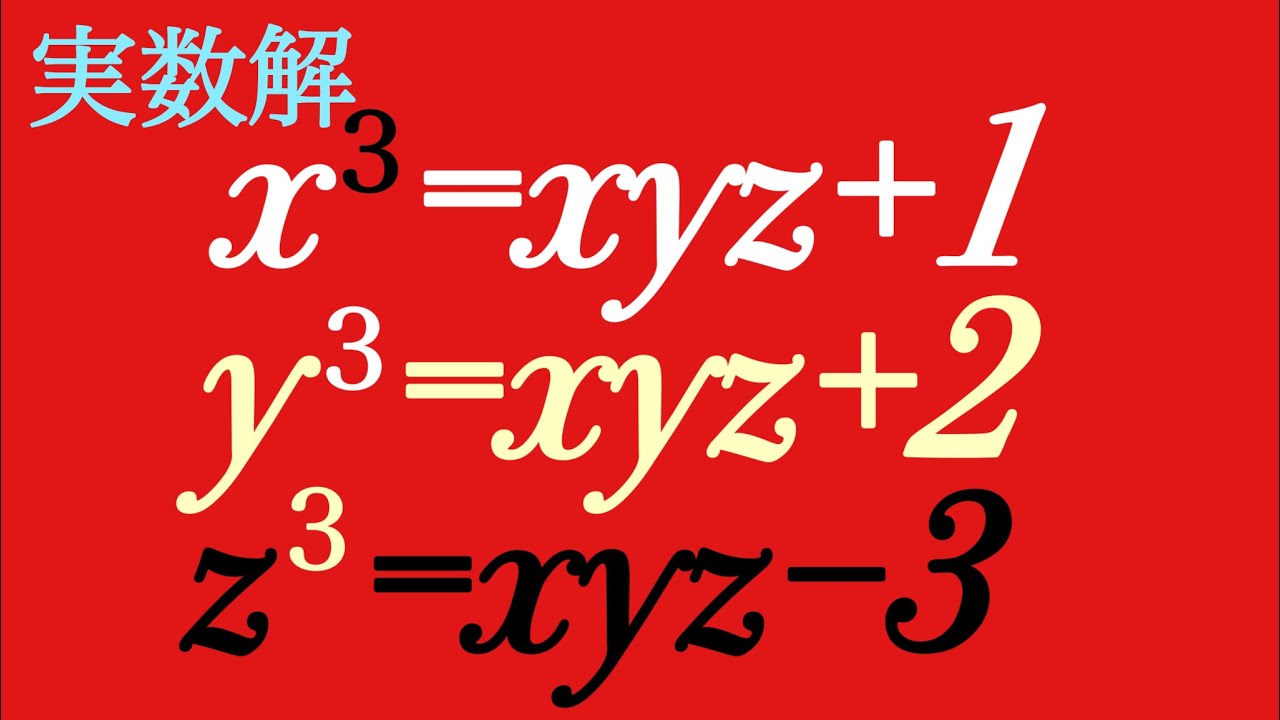
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3=xyz+1\\y^3=xyz+2 \\
z^3=xyz-3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3=xyz+1\\y^3=xyz+2 \\
z^3=xyz-3
\end{array}
\right.
\end{eqnarray}$
福田の数学〜早稲田大学2021年教育学部第1問〜高次方程式の実数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (1)方程式$x^4+5x^3-3x^2+4x+2=0$ は複素数$\displaystyle \frac{1+\sqrt3i}{2}$を解に持つ。
この方程式の実数解を全て求めよ。
2021早稲田大学教育学部過去問
この動画を見る
${\Large\boxed{1}}$ (1)方程式$x^4+5x^3-3x^2+4x+2=0$ は複素数$\displaystyle \frac{1+\sqrt3i}{2}$を解に持つ。
この方程式の実数解を全て求めよ。
2021早稲田大学教育学部過去問
3秒で答え出ます(剰余の定理)数II 割った余り
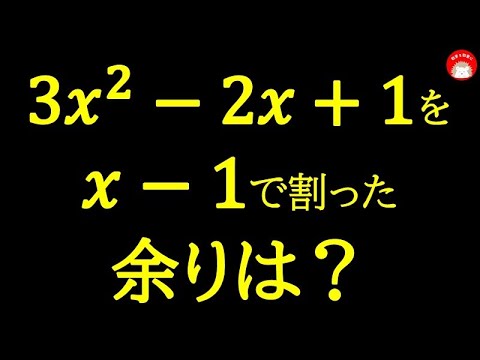
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$3x^2-2x+1$をx-1で割った余りは?
この動画を見る
$3x^2-2x+1$をx-1で割った余りは?
ざ・見掛け倒し 何次方程式?

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$f(x)=x^2+6x+6$
$f(f(f(f(f(x)))))=0$
この動画を見る
実数解を求めよ.
$f(x)=x^2+6x+6$
$f(f(f(f(f(x)))))=0$
ちょっと工夫 連立三元方程式
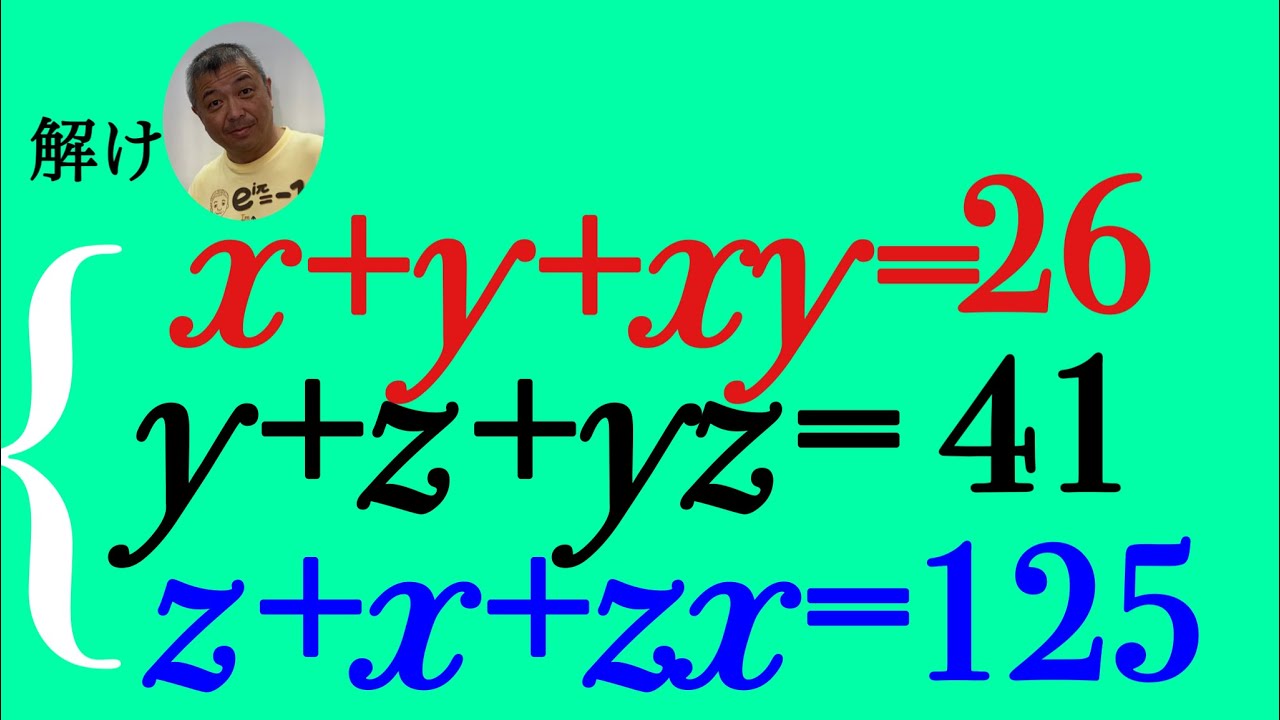
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+xy=26\\y+z+yz=41 \\
z+x+zx=125
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+xy=26\\y+z+yz=41 \\
z+x+zx=125
\end{array}
\right.
\end{eqnarray}$
3次方程式の解の7乗の和
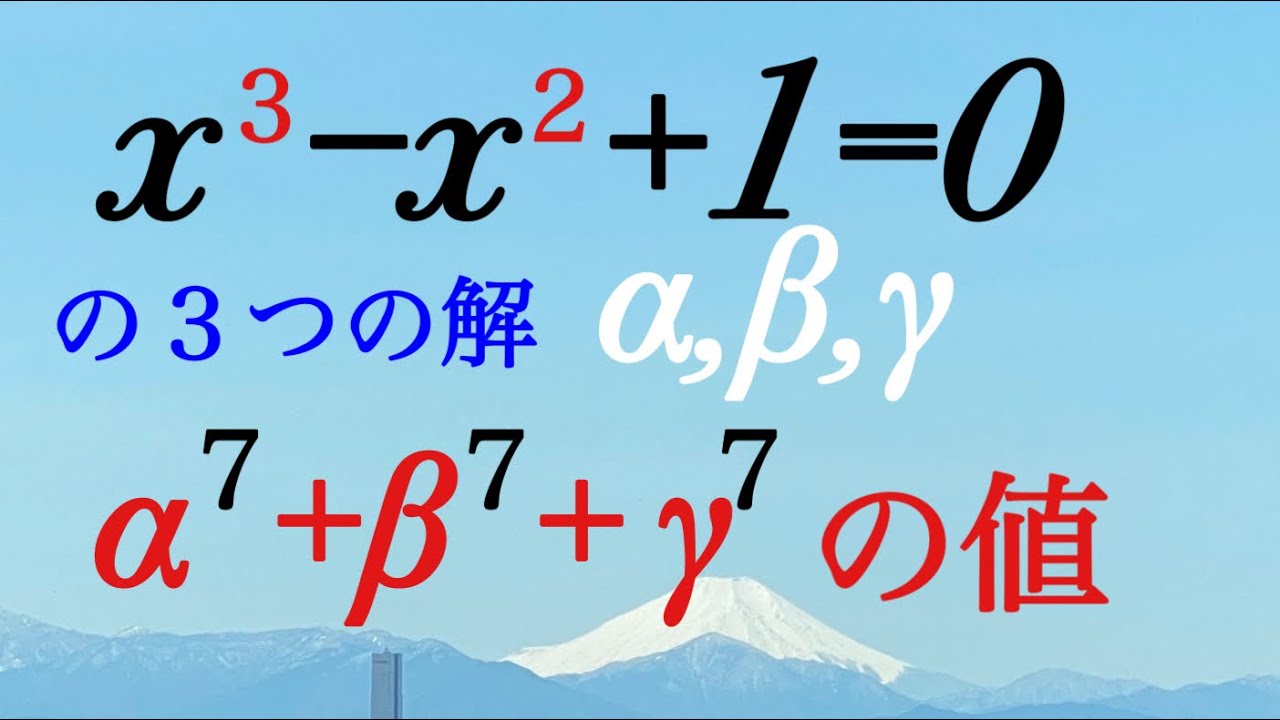
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-x^2+1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^7+\beta^7+\delta^7$の値を求めよ.
この動画を見る
$x^3-x^2+1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^7+\beta^7+\delta^7$の値を求めよ.
高校入試だけど3次方程式 動画内に誘導あり! 徳島文理(改)

単元:
#数学(中学生)#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
この動画を見る
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
方程式を解け。
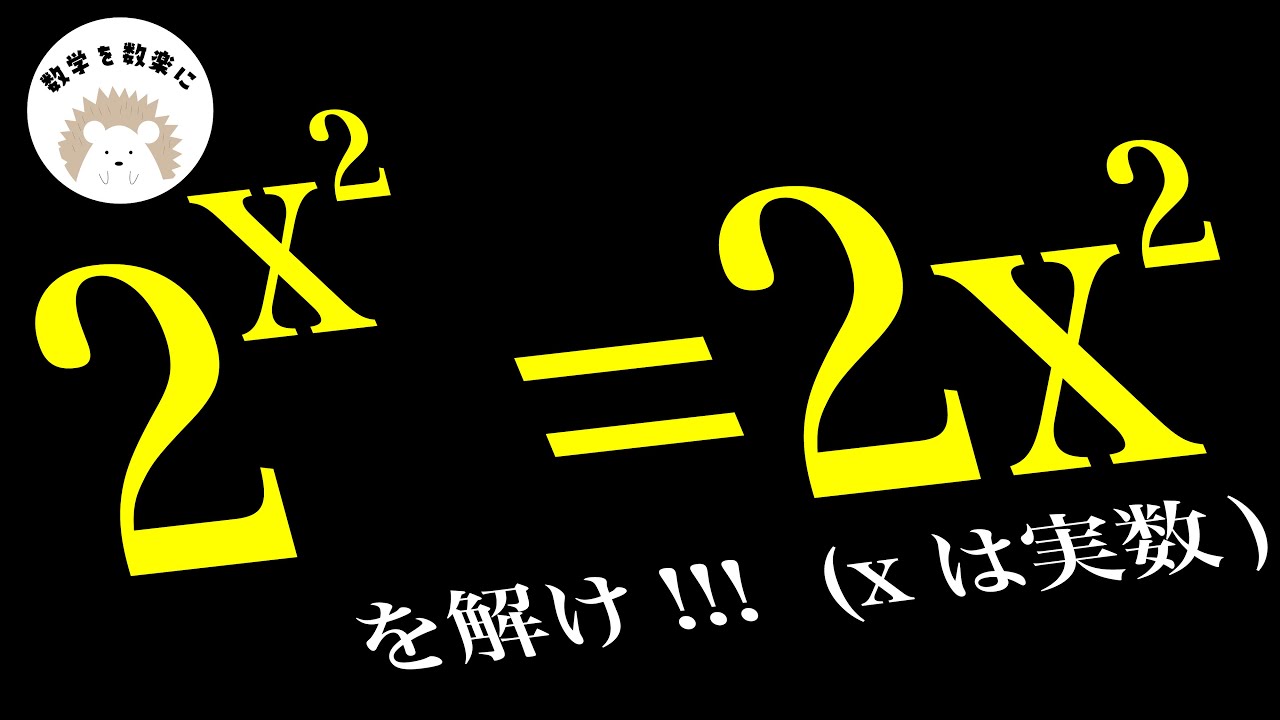
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x^{2}}=2x^2$を解け
(x:実数)
この動画を見る
$2^{x^{2}}=2x^2$を解け
(x:実数)
20滋賀県教員採用試験(数学:1-(3) 因数分解)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(3)$
$3x^3+(y-3)x^2-y$を因数分解せよ.
この動画を見る
$\boxed{1}-(3)$
$3x^3+(y-3)x^2-y$を因数分解せよ.
福田のわかった数学〜高校2年生012〜高次方程式の作成

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
$\alpha=\sqrt{13}+\sqrt{9+2\sqrt{17}}+$$\sqrt{9-2\sqrt{17}}$
を解にもつ整数係数であり$x^4$の係数1の
4次方程式を作れ。また、残りの解を求めよ。
この動画を見る
数学$\textrm{II}$ 高次方程式
$\alpha=\sqrt{13}+\sqrt{9+2\sqrt{17}}+$$\sqrt{9-2\sqrt{17}}$
を解にもつ整数係数であり$x^4$の係数1の
4次方程式を作れ。また、残りの解を求めよ。
福田のわかった数学〜高校2年生第9回〜高次方程式の有理数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
$a,b,c$を整数とするとき、3次方程式
$x^3+ax^2+bx+c=0$
が有理数解$s$をもつなら、$s$は整数である。
これを示せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
$a,b,c$を整数とするとき、3次方程式
$x^3+ax^2+bx+c=0$
が有理数解$s$をもつなら、$s$は整数である。
これを示せ。
#11数検1級1次過去問

単元:
#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$x^4-4x^3+x^2-3=0$を解け.
この動画を見る
$\boxed{1}$
$x^4-4x^3+x^2-3=0$を解け.
ただの4次方程式 その2

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$x^4+2x^2-400x=9991$
この動画を見る
これを解け.
$x^4+2x^2-400x=9991$
ただの4次方程式
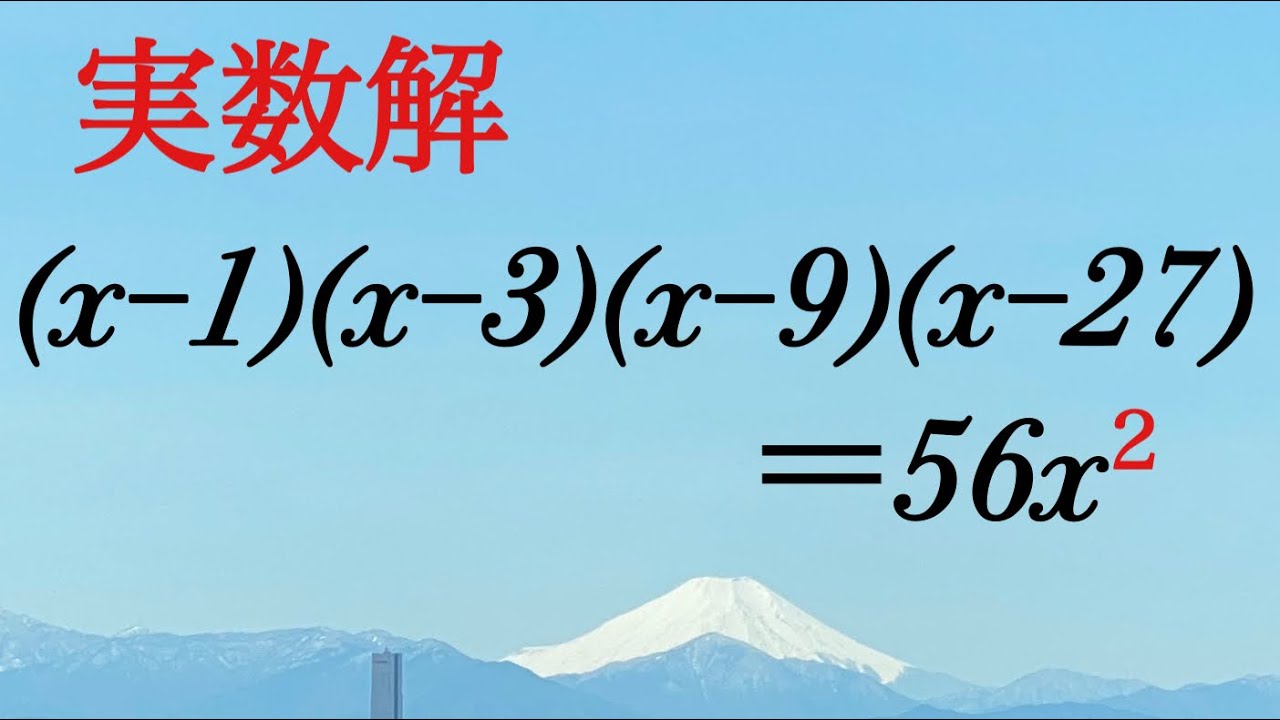
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
この動画を見る
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
06愛知県教員採用試験(数学:6番 指数)

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#整式の除法・分数式・二項定理#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$x$の方程式$4^x-2a\ 2^x+2a^2-a-6=0$が
正負が解を1つずつもつとき,
$a$の値の範囲を求めよ.
この動画を見る
$\boxed{6}$
$x$の方程式$4^x-2a\ 2^x+2a^2-a-6=0$が
正負が解を1つずつもつとき,
$a$の値の範囲を求めよ.
慶應(経済)実数解を持たない4次方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の$4$次方程式が実数解をもたない実数$a$の範囲を求めよ.
$x^4-ax^3+(-2a^2+a+4)x^2+(-2a^2+4a)x$
$+4a=0$
1999慶應(経)
この動画を見る
次の$4$次方程式が実数解をもたない実数$a$の範囲を求めよ.
$x^4-ax^3+(-2a^2+a+4)x^2+(-2a^2+4a)x$
$+4a=0$
1999慶應(経)
福田の1日1題わかった数学〜高校2年生第1回〜高次方程式

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
3次方程式$x^3+ax+b=0$の
3つの解を$\alpha,\beta,\gamma$とし、
$t_n=\alpha^n+\beta^n+\gamma^n$
のとき、$at_5+bt_4$を$a,b$で表せ。
12大阪府教員採用試験(数学:1 2 指数の方程式)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(2)$
$10^x=50^{y-1}$を
みたす有理数$x,y$を求めよ.
この動画を見る
$\boxed{1}-(2)$
$10^x=50^{y-1}$を
みたす有理数$x,y$を求めよ.
ただの3次方程式 複数の解法で

#5数検準1級1次過去問 指数

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
数学「大学入試良問集」【2−4 剰余の定理•商と余り】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$x$の整式$p(x)$を$x-3$で割った余りは$2,(x-2)^2$で割った余りは$x+1$である。
$p(x)$を$(x-2)^2$で割った商は$q(x)$とするとき、$q(x)$を$x-3$で割った余りを求めよ。
(2)
$p(x)$は(1)と同じ条件を満たすものとする。
このとき、$xp(x)$を$(x-3)(x-2)^2$で割った余りを求めよ。
この動画を見る
次の問いに答えよ。
(1)
$x$の整式$p(x)$を$x-3$で割った余りは$2,(x-2)^2$で割った余りは$x+1$である。
$p(x)$を$(x-2)^2$で割った商は$q(x)$とするとき、$q(x)$を$x-3$で割った余りを求めよ。
(2)
$p(x)$は(1)と同じ条件を満たすものとする。
このとき、$xp(x)$を$(x-3)(x-2)^2$で割った余りを求めよ。
数学「大学入試良問集」【2−2 高次方程式と解】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\alpha=\displaystyle \frac{3+\sqrt{ 7 }\ i}{2}$とする。
ただし、$i$は虚数単位である。次の問いに答えよ。
(1)
$\alpha$を解にもつような2次方程式$x^2+px+q=0(p,q$は整数)を求めよ。
(2)
整数$a,b,c$を係数とする3次方程式$x^3+ax^2+bx+c=0$について、解の1つは$\alpha$であり、また$0 \leqq x \leqq 1$の範囲に実数解を1つもつとする。
このような整数の組$(a,b,c)$を全て求めよ。
この動画を見る
$\alpha=\displaystyle \frac{3+\sqrt{ 7 }\ i}{2}$とする。
ただし、$i$は虚数単位である。次の問いに答えよ。
(1)
$\alpha$を解にもつような2次方程式$x^2+px+q=0(p,q$は整数)を求めよ。
(2)
整数$a,b,c$を係数とする3次方程式$x^3+ax^2+bx+c=0$について、解の1つは$\alpha$であり、また$0 \leqq x \leqq 1$の範囲に実数解を1つもつとする。
このような整数の組$(a,b,c)$を全て求めよ。
方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
この動画を見る
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
2021同志社大 4次方程式4つの虚数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
この動画を見る
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
2021早稲田 4次方程式の解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
この動画を見る
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
明治大 3倍角の公式と3次方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3$倍角の公式を利用して$x^3-3x-1=0$の$3$つの解を$cos$を用いて答えよ.
2020明治大過去問
この動画を見る
$3$倍角の公式を利用して$x^3-3x-1=0$の$3$つの解を$cos$を用いて答えよ.
2020明治大過去問
