複素数と方程式
複素数と方程式
【数Ⅱ】解と係数の関係と対称式 (2-α)(2-β)の値【もっとも簡単な解き方】
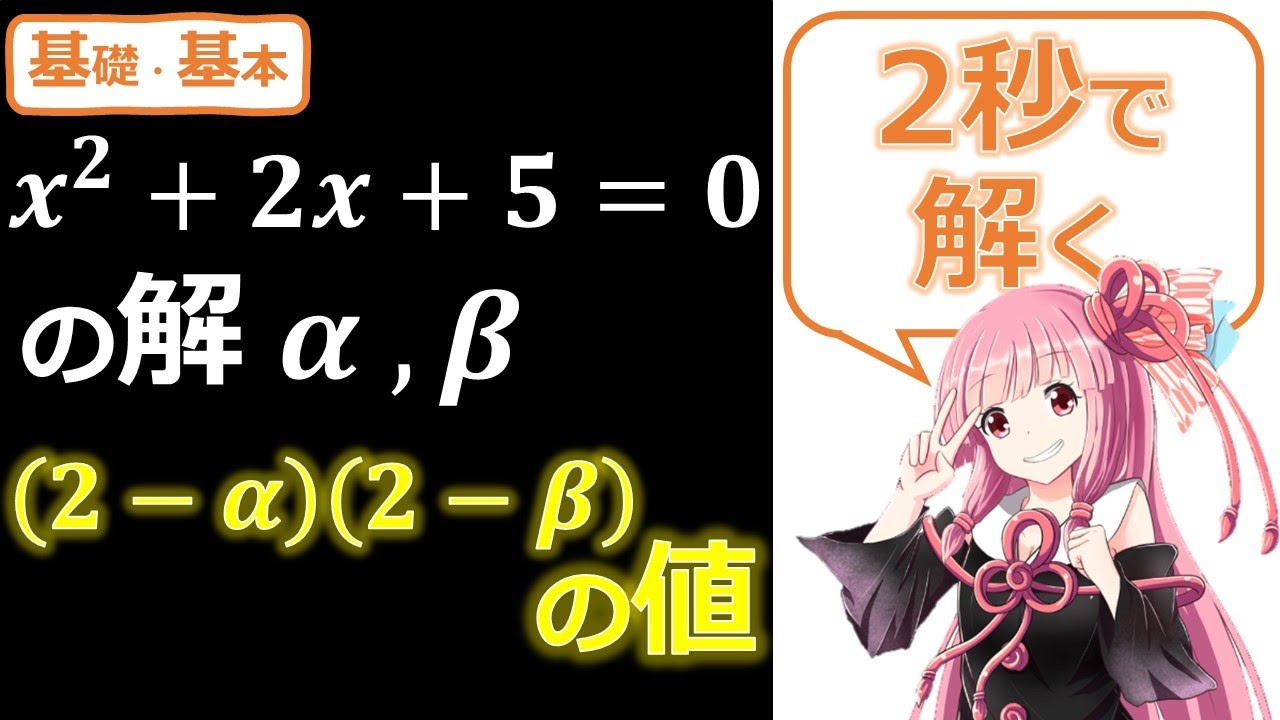
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ x^2+2x+5=0の解を\alpha,\betaとする.(2-\alpha)(2-\beta)を求めよ.$
この動画を見る
$ x^2+2x+5=0の解を\alpha,\betaとする.(2-\alpha)(2-\beta)を求めよ.$
11三重県教員採用試験（数学：1番 整数問題）
単元：
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
この動画を見る
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
#49 数検1級1次 過去問 根号を外す
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#２次関数#複素数と方程式#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
【数Ⅱ】解と係数の関係と対称式 α²+β²の値【複数の方法で理解を深める】
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ x^2+2x+5=0の解を\alpha,\betaとする.\alpha^2+\beta^2を求めよ.$
この動画を見る
$ x^2+2x+5=0の解を\alpha,\betaとする.\alpha^2+\beta^2を求めよ.$
【数Ⅱ】複素数の計算【簡単なようで間違えやすい計算】
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ iと等しいものを2つ選べ.
\dfrac{1}{i^3},\sqrt{-\dfrac{1}{2}}\sqrt{-2}i,\dfrac{1}{\sqrt{-1}},\dfrac{-3+2i}{2+3i}$
この動画を見る
$ iと等しいものを2つ選べ.
\dfrac{1}{i^3},\sqrt{-\dfrac{1}{2}}\sqrt{-2}i,\dfrac{1}{\sqrt{-1}},\dfrac{-3+2i}{2+3i}$
大学入試問題#60 広島工業大学(2021) 因数定理
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^{2019}+x^{2020}$を$x^2+x+1$で割った余りを求めよ。
出典：2021年広島工業大学 入試問題
この動画を見る
$x^{2019}+x^{2020}$を$x^2+x+1$で割った余りを求めよ。
出典：2021年広島工業大学 入試問題
どう解くか？だ。
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$0.2(0.1x -0.8) = \frac{4x+7}{50}$
法政大学
この動画を見る
方程式を解け
$0.2(0.1x -0.8) = \frac{4x+7}{50}$
法政大学
【数Ⅱ】虚数とは何か？【負×負=正となる理由、説明できる？】
大学入試問題#52 防衛医科大学(2020) 複素数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。
出典：2020年防衛医科大学 入試問題
この動画を見る
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。
出典：2020年防衛医科大学 入試問題
【因数定理】因数定理の使い方と原理を解説しました！〔数学、高校数学〕
#45 数検1級1次 過去問 複雑な方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$3x^2-12x+8=\displaystyle \frac{i\sqrt{ x-1 }}{\sqrt{ 3 }}$を満たす実数解$x$を求めよ
この動画を見る
$3x^2-12x+8=\displaystyle \frac{i\sqrt{ x-1 }}{\sqrt{ 3 }}$を満たす実数解$x$を求めよ
4次方程式
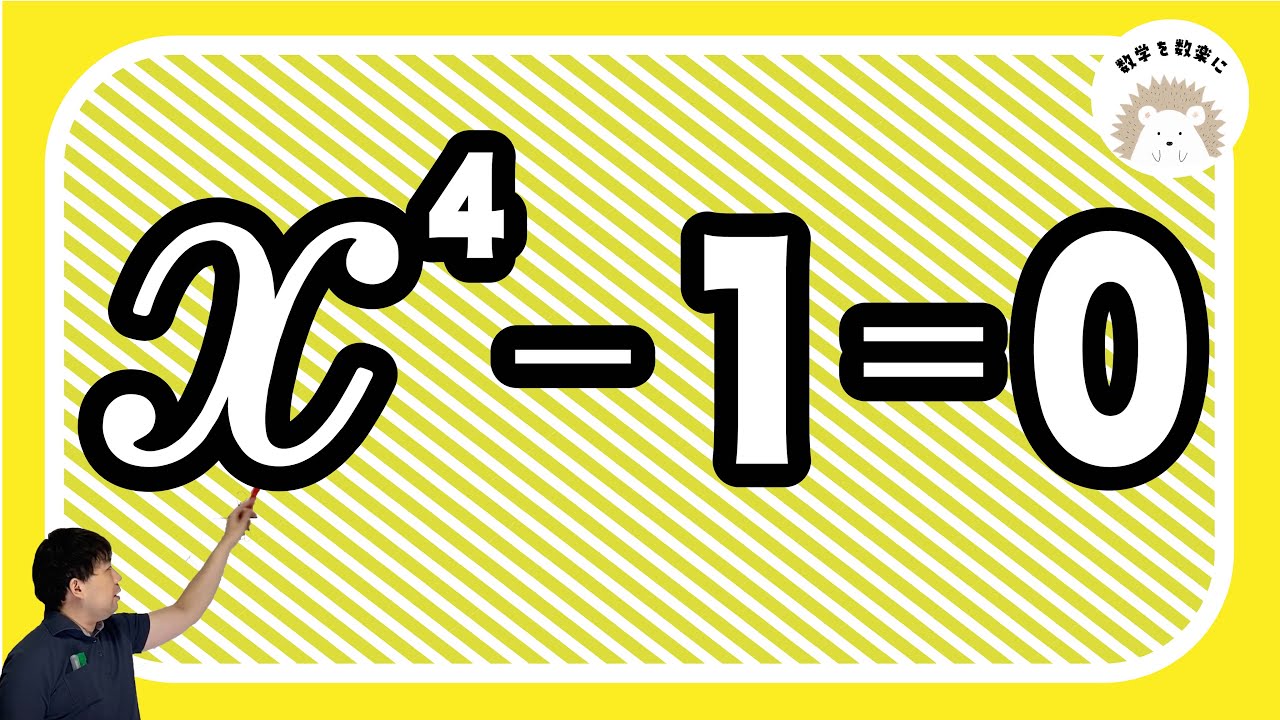
【2次方程式の知識はこれで完ペキ！】複素数と2次方程式の関係を解説！〔数学、高校数学〕
#38 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
この動画を見る
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
#35 数検１級１次 過去問 複素数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
この動画を見る
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
【複素数の基礎はこれだけ！】複素数の最低限の知識をまとめました！〔高校数学 数学〕
#32 数検1級1次 過去問 複素数の方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
この動画を見る
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
素数を探せ！10101‥101
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
素数を全て求めよ.
$101,10101,1010101,101010･･････101$
この動画を見る
素数を全て求めよ.
$101,10101,1010101,101010･･････101$
【数Ⅱ】剰余の定理と因数定理の使い方【3次方程式を解く・組立除法でちゃちゃっと計算】
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
剰余の定理と因数定理の使い方に関して解説していきます.
この動画を見る
剰余の定理と因数定理の使い方に関して解説していきます.
#29 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
この動画を見る
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
解けるように作られた９次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を求めよ.
$x=2+3(2+3x^3)^3$
この動画を見る
実数解を求めよ.
$x=2+3(2+3x^3)^3$
ただの４次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$(3x-2)^4+(3x-4)^4=16$
この動画を見る
これを解け.
$(3x-2)^4+(3x-4)^4=16$
福田のわかった数学〜高校２年生068〜三角関数(7)三角方程式とグラフ
単元：
#数Ⅱ#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(7) 三角方程式
$0 \leqq x \leqq 2\pi, 0 \leqq y \leqq 2\pi$において
$\cos y=\sin2x$ のグラフを描け。
この動画を見る
数学$\textrm{II}$ 三角関数(7) 三角方程式
$0 \leqq x \leqq 2\pi, 0 \leqq y \leqq 2\pi$において
$\cos y=\sin2x$ のグラフを描け。
福田のわかった数学〜高校２年生067〜三角関数(6)三角方程式
単元：
#数Ⅱ#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(6) 三角方程式
次の三角方程式の一般解と$0 \leqq \theta \lt 2\pi$における解を求めよ。
$\cos4\theta=\sin(\theta+\frac{\pi}{4})$
この動画を見る
数学$\textrm{II}$ 三角関数(6) 三角方程式
次の三角方程式の一般解と$0 \leqq \theta \lt 2\pi$における解を求めよ。
$\cos4\theta=\sin(\theta+\frac{\pi}{4})$
福田のわかった数学〜高校２年生066〜三角関数(5)三角方程式
単元：
#数Ⅱ#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(5) 三角方程式
定角$\alpha$に対して次の一般解を求めよ。
(1)$\sin x=\sin\alpha$ (2)$\cos x=\cos\alpha$
(3)$\tan x=\tan\alpha$
この動画を見る
数学$\textrm{II}$ 三角関数(5) 三角方程式
定角$\alpha$に対して次の一般解を求めよ。
(1)$\sin x=\sin\alpha$ (2)$\cos x=\cos\alpha$
(3)$\tan x=\tan\alpha$
福田のわかった数学〜高校２年生064〜三角関数(3)三角方程式の基礎
単元：
#数Ⅱ#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(3) 三角方程式の基礎
(1)$\sin\theta=-\frac{1}{2}$ (2)$\cos\theta=\frac{\sqrt3}{2}$ (3)$\tan\theta=-1$
の解を(ア)$0 \leqq \theta \lt 2\pi$ (イ)$-\pi \leqq \theta \lt \pi$
(ウ)一般解 としてそれぞれ求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(3) 三角方程式の基礎
(1)$\sin\theta=-\frac{1}{2}$ (2)$\cos\theta=\frac{\sqrt3}{2}$ (3)$\tan\theta=-1$
の解を(ア)$0 \leqq \theta \lt 2\pi$ (イ)$-\pi \leqq \theta \lt \pi$
(ウ)一般解 としてそれぞれ求めよ。
【数Ⅱ】複素数と方程式：x²+x+1=0の２解をα、βとする。(1)α＋β(2)α³＋β³(3)α¹⁰⁰＋β¹⁰⁰の値を求めよ。
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x^2+x+1=0$の2解を$\alpha,\beta$とする。
(1)$\alpha+\beta$
(2)$\alpha^3+\beta^3$
(3)$\alpha^{100}+\beta^{100}$の値を求めよ。
この動画を見る
$x^2+x+1=0$の2解を$\alpha,\beta$とする。
(1)$\alpha+\beta$
(2)$\alpha^3+\beta^3$
(3)$\alpha^{100}+\beta^{100}$の値を求めよ。
福田の数学〜明治大学2021年理工学部第１問(1)〜2次方程式が整数を解にもつ条件
単元：
#数Ⅰ#数A#数Ⅱ#２次関数#複素数と方程式#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
【数Ⅱ】複素数と方程式：解と係数の関係(3次)の利用
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
3次方程式$x^3+ax^2+bx+20=0$の解の1つが$x=3-i$であるとき、実数の定数a,bの値と、他の解を求めよう。
この動画を見る
3次方程式$x^3+ax^2+bx+20=0$の解の1つが$x=3-i$であるとき、実数の定数a,bの値と、他の解を求めよう。
解けるように作られた五次方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$(x-1)^5+(x+3)^5=328(x+1)$
この動画を見る
これを解け.
$(x-1)^5+(x+3)^5=328(x+1)$