点と直線
点と直線
福田の数学〜慶應義塾大学看護医療学部2025第4問〜放物線と接線の囲む面積と内積の最小値
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$k$を実数の定数とし、
座標平面上に$2$点$A(1,-3),B(-1,k)$をとる。
また、放物線$y=x^2$を$C$とする。
以下に答えなさい。
(1)点$A$から曲線$C$に引いた$2$本の接線のうち、
傾きが正の接線を$\ell_1$とし、
傾きが負の接線を$\ell_2$とするとき、
直線$\ell_1$の方程式は$y=\boxed{テ}$であり、
直線$\ell_2$の方程式は$y=\boxed{ト}$である。
また、$2$直線$\ell_1,\ell_2$のなす角を$\theta$とすると、
$\tan\theta=\boxed{ナ}$である。
ただし、$0\lt\theta\lt\dfrac{\pi}{2}$とする。
さらに、曲線$C$と$2$直線$\ell_1,\ell_2$で囲まれた
図形の面積は$\boxed{ニ}$である。
(2)点$P$が曲線$C$全体を動くときの
$\overrightarrow{PA}･\overrightarrow{PB}$の最小値を$m$とする。
このとき、$m$を$k$を用いて表すと、
$k\geqq \boxed{ヌ}$のときは$m=\boxed{ネ}$であり、
$k\lt \boxed{ヌ}$のときは、$m=\boxed{ノ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{4}$
$k$を実数の定数とし、
座標平面上に$2$点$A(1,-3),B(-1,k)$をとる。
また、放物線$y=x^2$を$C$とする。
以下に答えなさい。
(1)点$A$から曲線$C$に引いた$2$本の接線のうち、
傾きが正の接線を$\ell_1$とし、
傾きが負の接線を$\ell_2$とするとき、
直線$\ell_1$の方程式は$y=\boxed{テ}$であり、
直線$\ell_2$の方程式は$y=\boxed{ト}$である。
また、$2$直線$\ell_1,\ell_2$のなす角を$\theta$とすると、
$\tan\theta=\boxed{ナ}$である。
ただし、$0\lt\theta\lt\dfrac{\pi}{2}$とする。
さらに、曲線$C$と$2$直線$\ell_1,\ell_2$で囲まれた
図形の面積は$\boxed{ニ}$である。
(2)点$P$が曲線$C$全体を動くときの
$\overrightarrow{PA}･\overrightarrow{PB}$の最小値を$m$とする。
このとき、$m$を$k$を用いて表すと、
$k\geqq \boxed{ヌ}$のときは$m=\boxed{ネ}$であり、
$k\lt \boxed{ヌ}$のときは、$m=\boxed{ノ}$である。
$2025$年慶應義塾大学看護医療学部過去問題
【数Ⅱ】【図形と方程式】2直線の関係3 ※問題文は概要欄
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問1
直線$y=2x$を$l$とするとき､次のものを求めよ｡
(1)$l$に関して､点$\rm A(5,0)$と対称な点Bの座標
(2) $l$に関して､直線$3x+y=15$と対称な直線の方程式
問２
$k$を定数とする｡直線$(k+2)x+(2k-3)y=5k-4$は$k$の値に関係なく定点を通る｡その定点の座標を求めよ｡
問３
$x-y=1,2x-3y=1,ax+by=1$が1点で交わらなければ､3点$(1,ｰ1),(2,ｰ3),(a,b)$は一直線上にあることを証明せよ｡
この動画を見る
問1
直線$y=2x$を$l$とするとき､次のものを求めよ｡
(1)$l$に関して､点$\rm A(5,0)$と対称な点Bの座標
(2) $l$に関して､直線$3x+y=15$と対称な直線の方程式
問２
$k$を定数とする｡直線$(k+2)x+(2k-3)y=5k-4$は$k$の値に関係なく定点を通る｡その定点の座標を求めよ｡
問３
$x-y=1,2x-3y=1,ax+by=1$が1点で交わらなければ､3点$(1,ｰ1),(2,ｰ3),(a,b)$は一直線上にあることを証明せよ｡
【数Ⅱ】【図形と方程式】2直線の関係2 ※問題文は概要欄
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$3x-2y+3=0,2x-4y+k=0,x-ky+5=0$が1点で交わるように､定数$k$の値を求めよ｡
$x+3y=2,x+y=0,ax+2y=-4$が三角形を作らないような定数$a$の値を求めよ｡
2直線$x-y+1=0,3x+2y-12=0$の交点を通り､次の条件を満たす直線の方程式を､それぞれ求めよ｡
(1)直線$5xｰ6yｰ8=0$に平行である｡
(2)直線$5xｰ6yｰ8=0$に垂直である｡
この動画を見る
$3x-2y+3=0,2x-4y+k=0,x-ky+5=0$が1点で交わるように､定数$k$の値を求めよ｡
$x+3y=2,x+y=0,ax+2y=-4$が三角形を作らないような定数$a$の値を求めよ｡
2直線$x-y+1=0,3x+2y-12=0$の交点を通り､次の条件を満たす直線の方程式を､それぞれ求めよ｡
(1)直線$5xｰ6yｰ8=0$に平行である｡
(2)直線$5xｰ6yｰ8=0$に垂直である｡
【数Ⅱ】【図形と方程式】2直線の関係1 ※問題文は概要欄
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
三角形$\rm ABC$について次の三直線の方程式を求めよ。またそれらが1点で交わることを示し、その点の座標を求めよ。
(1) 各辺の垂直二等分線
(2) 各頂点から対辺に下した垂線
$x+ay+1=0, ax+(a+2)y+3=0$ が次の条件を満たすとき定数$a$の値をそれぞれ求めよ。
(1) 平行である
(2) 垂直である
この動画を見る
三角形$\rm ABC$について次の三直線の方程式を求めよ。またそれらが1点で交わることを示し、その点の座標を求めよ。
(1) 各辺の垂直二等分線
(2) 各頂点から対辺に下した垂線
$x+ay+1=0, ax+(a+2)y+3=0$ が次の条件を満たすとき定数$a$の値をそれぞれ求めよ。
(1) 平行である
(2) 垂直である
【数Ⅱ】【図形と方程式】内分外分の利用 ※問題文は概要欄
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
3点$(2,-2),(-1,1),\rm C$を頂点とする三角形が正三角形になるとき、点$\rm C$の座標を求めよ。
3点$(3,5),(2,-2),-(6,2)$から等距離にある点の座標を求めよ。
(1) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形$\rm ABCD$ がある。対角線$\rm AC,BD$の交点及び、頂点$\rm D$の座標を求めよ。
(2) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形について、頂点$\rm D$となりうる点の座標をすべて答えよ。
この動画を見る
3点$(2,-2),(-1,1),\rm C$を頂点とする三角形が正三角形になるとき、点$\rm C$の座標を求めよ。
3点$(3,5),(2,-2),-(6,2)$から等距離にある点の座標を求めよ。
(1) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形$\rm ABCD$ がある。対角線$\rm AC,BD$の交点及び、頂点$\rm D$の座標を求めよ。
(2) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形について、頂点$\rm D$となりうる点の座標をすべて答えよ。
【数Ⅱ】【図形と方程式】内分と外分の基本、点と直線 ※問題文は概要欄
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2点$\rm A(-5),B(11)$に対して、線分$\rm AB$を$5:3$に内分する点を$\rm P$、$7:11$に外分する点を$\rm Q$とする。線分$\rm PQ$の中点の座標を求めよ。
次の3点が一直線上にあるとき、$t$の値を求めよ。
(1) $(-2,6),(0,3),(4,t)$
(2) $(1,4),(-1,t),(t,2)$
この動画を見る
2点$\rm A(-5),B(11)$に対して、線分$\rm AB$を$5:3$に内分する点を$\rm P$、$7:11$に外分する点を$\rm Q$とする。線分$\rm PQ$の中点の座標を求めよ。
次の3点が一直線上にあるとき、$t$の値を求めよ。
(1) $(-2,6),(0,3),(4,t)$
(2) $(1,4),(-1,t),(t,2)$
【数Ⅱ】【図形と方程式】内分外分重心 ※問題文は概要欄
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
三角形の各辺の中点の座標を$(-1,-1),(-0,-1),(2,-2)$であるとき、この三角形の3つの頂点の座標を求めよ。
$\triangle \rm ABC$の重心を$\rm G$とするとき、次の等式を証明せよ。$\rm AB^2＋AC^2＝BG^2＋CG^2＋４AG^2$
$\triangle \rm ABC$において辺$\rm AB,BC,CA$を$3:2$に内分する点を、それぞれ$\rm D,E,F$とするとき、$\triangle \rm ABC$と$\triangle \rm DEF$の重心は一致することを証明せよ。
この動画を見る
三角形の各辺の中点の座標を$(-1,-1),(-0,-1),(2,-2)$であるとき、この三角形の3つの頂点の座標を求めよ。
$\triangle \rm ABC$の重心を$\rm G$とするとき、次の等式を証明せよ。$\rm AB^2＋AC^2＝BG^2＋CG^2＋４AG^2$
$\triangle \rm ABC$において辺$\rm AB,BC,CA$を$3:2$に内分する点を、それぞれ$\rm D,E,F$とするとき、$\triangle \rm ABC$と$\triangle \rm DEF$の重心は一致することを証明せよ。
福田の数学〜明治大学2024理工学部第3問〜放物線と折れ線の位置関係
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
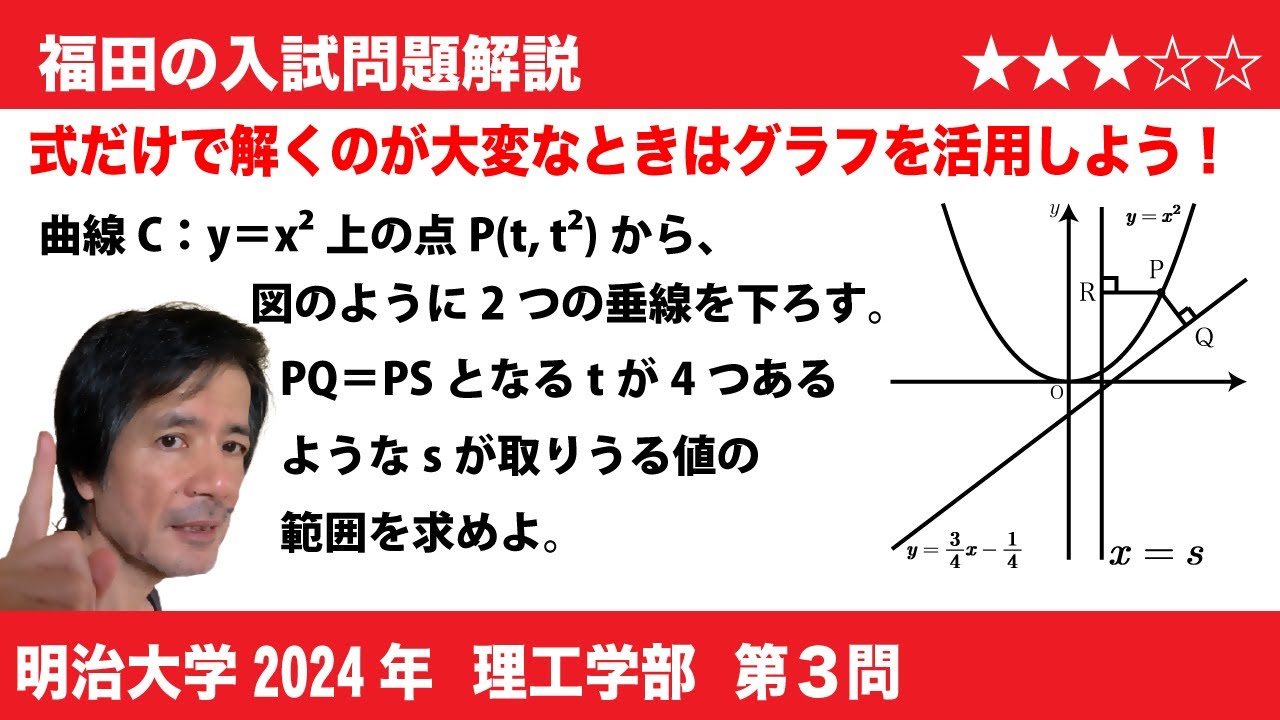
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
この動画を見る
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
定点の座標を求めよ 高校数学
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
定数kがどんな値を取っても
直線$kx-y+5k=0$が通る
定点の座標を求めよ
この動画を見る
定数kがどんな値を取っても
直線$kx-y+5k=0$が通る
定点の座標を求めよ
福田の数学〜浜松医科大学2024医学部第4問〜直線に関する対称点と絶対不等式
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#軌跡と領域#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める（図は動画内参照）。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
この動画を見る
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める（図は動画内参照）。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
難関高校受験生必見！！放物線と比
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$y=x^2$ $\quad$ $y=\frac{1}{4}x^2$
a:b=?
＊図は動画内参照
この動画を見る
$y=x^2$ $\quad$ $y=\frac{1}{4}x^2$
a:b=?
＊図は動画内参照
高校数学：数学検定準1級1次:問題1,2 :対数不等式、2直線間の距離
単元：
#数Ⅱ#図形と方程式#指数関数と対数関数#点と直線#対数関数#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題１
次の不等式を解きなさい。
$\log_{ \frac{1}{2}} 2x ＞\log_{ \frac{1}{2}} x^2-2x+3$
問題２
xy平面上の２直線$3x＋4y－20＝0$と$3x＋4y＋50＝0$の間の距離を求めなさい。
この動画を見る
問題１
次の不等式を解きなさい。
$\log_{ \frac{1}{2}} 2x ＞\log_{ \frac{1}{2}} x^2-2x+3$
問題２
xy平面上の２直線$3x＋4y－20＝0$と$3x＋4y＋50＝0$の間の距離を求めなさい。
福田の数学〜双曲線と直線の位置関係を考えよう〜明治大学2023年全学部統一Ⅲ第3問〜双曲線と直線
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
この動画を見る
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
【わかりやすく】直線に対して対象の点の座標を求めよう（数学Ⅱ 図形と方程式）
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
直線$y=x+3$に対して、点$A(-2,4)$と対称な点の座標を求めよ。
この動画を見る
直線$y=x+3$に対して、点$A(-2,4)$と対称な点の座標を求めよ。
【短時間でマスター!!】直線の方程式(平行と垂直)の求め方を解説！〔現役講師解説、数学〕
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
数学2B
直線の方程式
並行と垂直の条件
①点$(1,-3)$を通り、直線$4x+5y=2$に平行な直線
②点$(0,1)$を通り、直線$y=-3x-1$に垂直な直線
この動画を見る
数学2B
直線の方程式
並行と垂直の条件
①点$(1,-3)$を通り、直線$4x+5y=2$に平行な直線
②点$(0,1)$を通り、直線$y=-3x-1$に垂直な直線
サッカーボールの頂点の個数は？ 共栄学園（東東京）
単元：
#数Ⅱ#点と直線#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
12個の正五角形と20個の正六角形の合わせて32面からなる多面体
どの頂点にも1個の正五角形と2個の正六角形の面が集まっている
この多面体の頂点の個数は？
共栄学園高等学校
この動画を見る
12個の正五角形と20個の正六角形の合わせて32面からなる多面体
どの頂点にも1個の正五角形と2個の正六角形の面が集まっている
この多面体の頂点の個数は？
共栄学園高等学校
内角を二等分する直線の式 立教新座
福田の数学〜立教大学2023年経済学部第3問〜放物線と直線で囲まれた図形の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#面積、体積#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
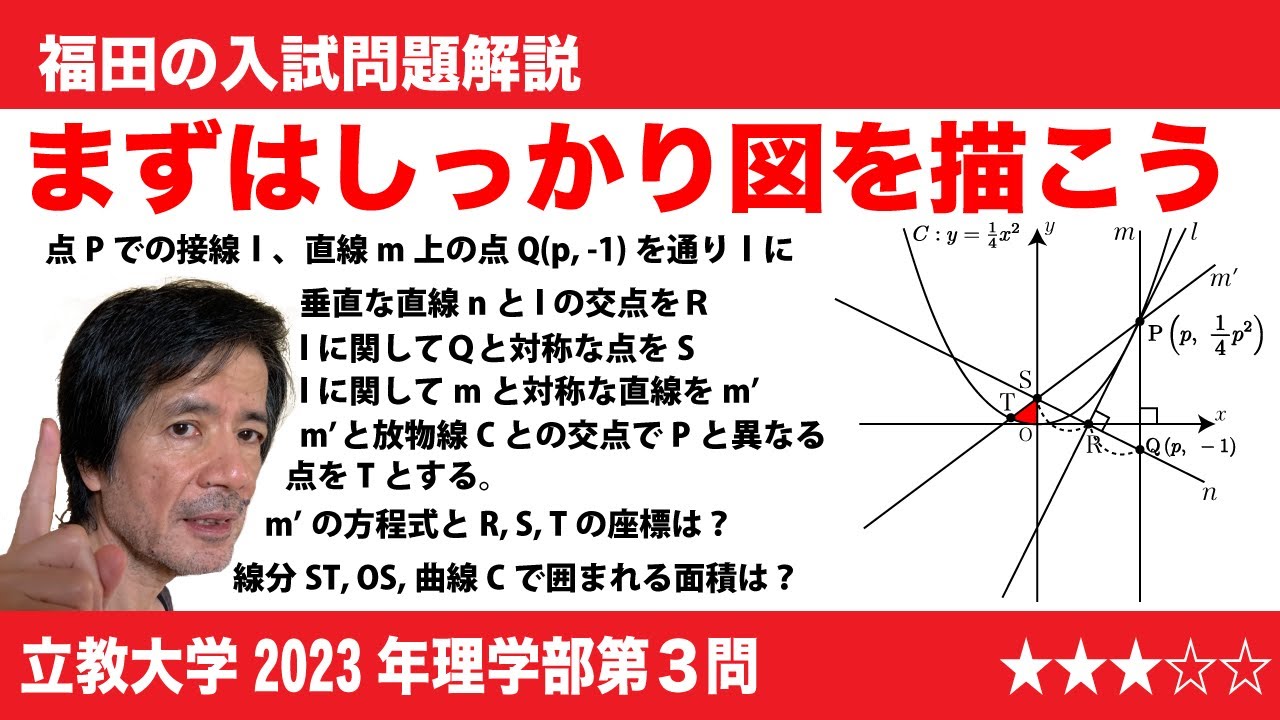
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C：$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
この動画を見る
$\Large\boxed{3}$ pを正の実数とする。Oを原点とする座標平面上の放物線C：$y$=$\frac{1}{4}x^2$上の点P$\left(p, \frac{1}{4}p^2\right)$における接線を$l$、Pを通り$x$軸に垂直な直線を$m$とする。また、$m$上の点Q$\left(p, -1\right)$を通り$l$に垂直な直線を$n$とし、$l$と$n$の交点をRとする。さらに、$l$に関してQと対称な点をSとする。このとき、次の問いに答えよ。
(1)$l$の方程式を$p$を用いて表せ。
(2)$n$の方程式およびRの座標をそれぞれ$p$を用いて表せ。
(3)Sの座標を求めよ。
(4)$l$を対象軸として、$l$に関して$m$と対称な直線$m'$の方程式を$p$を用いて表せ。
また、$m'$とCの交点のうちPと異なる点をTとするとき、Tの$x$座標を$p$を用いて表せ。
(5)(4)のTに対して、線分ST、線分OSおよびCで囲まれた部分の面積を$p$を用いて表せ。
【数Ⅱ】間違えやすい？ 点と直線の距離の公式の覚え方
単元：
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
この動画を見る
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
慶應義塾大 直線の傾き
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2016慶応義塾大学過去問題
aは整数、aの値は？
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
この動画を見る
2016慶応義塾大学過去問題
aは整数、aの値は？
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
福田の数学〜筑波大学2023年理系第1問〜３次関数の接線と三角形の面積
単元：
#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#平均変化率・極限・導関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#筑波大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 曲線C：$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2＜$t$＜1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2＜$t$＜1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{1}$ 曲線C：$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2＜$t$＜1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2＜$t$＜1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
福田の数学〜慶應義塾大学2023年医学部第１問(3)〜曲線と直線で囲まれた面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (3)曲線y=$x$$\log(x^2+1)$のx≧0の部分をCとすると、点(1, log2)におけるCの接線lの方程式はy=$\boxed{\ \ く\ \ }$である。
また、曲線Cと直線l、およびy軸で囲まれた図形の面積は$\boxed{\ \ け\ \ }$である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (3)曲線y=$x$$\log(x^2+1)$のx≧0の部分をCとすると、点(1, log2)におけるCの接線lの方程式はy=$\boxed{\ \ く\ \ }$である。
また、曲線Cと直線l、およびy軸で囲まれた図形の面積は$\boxed{\ \ け\ \ }$である。
2023慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年医学部第１問(1)〜図形の証明
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#図形と計量#三角比への応用（正弦・余弦・面積）#図形と方程式#恒等式・等式・不等式の証明#点と直線#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4：3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4：3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年薬学部第１問(2)〜折れ線の最小と内接円の半径
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#三角関数#点と直線#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l：y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l：y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
福田の数学〜北海道大学2023年理系第５問〜中間値の定理と関数の増減PART1
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ a,bを$a^2$+$b^2$＜1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0＜θ＜$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0＜θ＜$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0＜θ＜$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$＜1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0＜θ＜$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0＜θ＜$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0＜θ＜$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
福田の数学〜東京大学2023年文系第２問〜定積分で表された関数と最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
福田の数学〜東京工業大学2023年理系第５問(PART1)〜4直線に接する球面の決定
単元：
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#点と直線#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題083〜東北大学2018年度理系第１問〜直線の通過範囲
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ xy平面上における2つの放物線C：y=$(x-a)^2+b$, D：y=$-x^2$を考える。
(1)CとDが異なる2点で交わり、その2交点のx座標の差が1となるように実数a,bが動くとき、Cの頂点(a, b)の軌跡を図示せよ。
(2)実数a, bが(1)の条件を満たしながら動くとき、CとDの2交点を結ぶ直線が通過する範囲を定め、図示せよ。
2018東北大学理系過去問
この動画を見る
$\Large\boxed{1}$ xy平面上における2つの放物線C：y=$(x-a)^2+b$, D：y=$-x^2$を考える。
(1)CとDが異なる2点で交わり、その2交点のx座標の差が1となるように実数a,bが動くとき、Cの頂点(a, b)の軌跡を図示せよ。
(2)実数a, bが(1)の条件を満たしながら動くとき、CとDの2交点を結ぶ直線が通過する範囲を定め、図示せよ。
2018東北大学理系過去問
福田の1.5倍速演習〜合格する重要問題097〜早稲田大学2020年度教育学部第４問〜曲線の通過範囲の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ 座標平面上で、定数k＞0に対し、曲線y=$\frac{k}{\sqrt{1+x^2}}$の0≦x≦1の部分を$C_k$とする。
(1)曲線$C_k$上の点と原点との距離の最大値$M(k)$を求めよ。
(2)原点を中心に曲線$C_k$を1回転させるとき、$C_k$が通る部分の面積$S(k)$を求めよ。
2020早稲田大学教育学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面上で、定数k＞0に対し、曲線y=$\frac{k}{\sqrt{1+x^2}}$の0≦x≦1の部分を$C_k$とする。
(1)曲線$C_k$上の点と原点との距離の最大値$M(k)$を求めよ。
(2)原点を中心に曲線$C_k$を1回転させるとき、$C_k$が通る部分の面積$S(k)$を求めよ。
2020早稲田大学教育学部過去問
福田の1.5倍速演習〜合格する重要問題049〜早稲田大学2019年度商学部第２問〜折れ線の長さの最小値問題
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#図形と方程式#微分法と積分法#点と直線#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
この動画を見る
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問