 三角関数
三角関数
 三角関数
三角関数
福田の数学〜青山学院大学2025理工学部第3問〜三角関数のグラフと面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$f(x)=\cos^3 x+\sin^3 x,g(x)=\sin x$とする。
(1)$0\leqq x \leqq \pi$において、
曲線$y=f(x)$の概形を描け。
ただし、凹凸は調べなくてよい。
(2)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$の共有点の座標を求めよ。
(3)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$で囲まれた図形の
面積$S$を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{3}$
$f(x)=\cos^3 x+\sin^3 x,g(x)=\sin x$とする。
(1)$0\leqq x \leqq \pi$において、
曲線$y=f(x)$の概形を描け。
ただし、凹凸は調べなくてよい。
(2)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$の共有点の座標を求めよ。
(3)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$で囲まれた図形の
面積$S$を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜早稲田大学2025社会科学部第3問〜三角関数の最大最小と三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
福田の数学〜九州大学2025文系第2問〜円周上の2点との距離の2乗の和の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#三角関数#三角関数とグラフ#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
この動画を見る
$\boxed{2}$
半径$1$の円周$C$上の$2$点$A,B$は
$AB=\sqrt3$をみたすとする。
点$P$が円周$C$上を動くとき、
$AP^2+BP^2$の最大値を求めよ。
$2025$年九州大学文系過去問題
福田の数学〜神戸大学2025文系第3問〜単位円周上の2点と確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#場合の数#三角関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
福田のおもしろ数学530〜三角関数の最大値

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
この動画を見る
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
福田の数学〜立教大学2025理学部第2問〜三角関数の最大最小の定番

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
福田の数学〜立教大学2025経済学部第2問〜2点の位置関係と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{2}$
$p,q$を正の実数とする。
原点を$O$とする座標平面上に
点$A(1,0)$、点$P\left(p,\dfrac{1}{p}\right)$,点$Q\left(q,\dfrac{2}{q}\right)$がある。
$\angle AOP=\alpha,\angle AOQ=\beta$とおき、
$P,Q$は$\alpha \lt \beta$を満たしながら動くものとする。
三角形$OPQ$の面積を$S$とし、
また、$T=\tan(\beta-\alpha)$とおく。
(1)$\cos\alpha,\sin\alpha$をそれぞれ$p$を用いて表せ。
また、$\cos\beta,\sin\beta$をそれぞれ$q$を用いて表せ。
(2)$T$を$p,q$を用いて表せ。
(3)$S$を$p,q$を用いて表せ。
(4)$t=pq$とおく。$\dfrac{S}{T}$を$t$を用いて表せ。
(5)$\dfrac{S}{T}$の最小値を求めよ。
$2025$年立教大学経済学部過去問題
福田のおもしろ数学504〜三角関数の最大値

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$がすべての実数を動くとき
$\sin(\cos x)+\cos(\sin x)$の最大値を求めよ。
この動画を見る
$x$がすべての実数を動くとき
$\sin(\cos x)+\cos(\sin x)$の最大値を求めよ。
福田のおもしろ数学491〜三角関数の連立方程式

単元:
#連立方程式#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y$は実数であり
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x+\cos y=1 \\
\cos x+\sin y=-1
\end{array}
\right.
\end{eqnarray}$
のとき、$\cos 2x=\cos 2y$となることを
証明せよ。
この動画を見る
$x,y$は実数であり
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x+\cos y=1 \\
\cos x+\sin y=-1
\end{array}
\right.
\end{eqnarray}$
のとき、$\cos 2x=\cos 2y$となることを
証明せよ。
福田のおもしろ数学489〜3本の光線のなす角と三角関数

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$3$本の光線が原点$O$から空間へ発射された。
$2$本ずつのなす角が
$\alpha,\beta,\gamma(0° \lt \alpha \leqq \beta \leqq \gamma \leqq 180°)$
であり、この$3$本の光線は同一平面上にない。
$\sin\dfrac{\alpha}{2}+\sin\dfrac{\beta}{2} \gt \sin\dfrac{\gamma}{2}$
を証明せよ。
この動画を見る
$3$本の光線が原点$O$から空間へ発射された。
$2$本ずつのなす角が
$\alpha,\beta,\gamma(0° \lt \alpha \leqq \beta \leqq \gamma \leqq 180°)$
であり、この$3$本の光線は同一平面上にない。
$\sin\dfrac{\alpha}{2}+\sin\dfrac{\beta}{2} \gt \sin\dfrac{\gamma}{2}$
を証明せよ。
福田のおもしろ数学487〜三角関数のシグマ計算の必殺テクニック

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
任意の自然数$m$に対して
$\displaystyle \sum_{k=1}^{m} (-1)^k \cos \dfrac{k\pi}{2m+1}=-\dfrac{1}{2}$
が成り立つことを証明して下さい。
この動画を見る
任意の自然数$m$に対して
$\displaystyle \sum_{k=1}^{m} (-1)^k \cos \dfrac{k\pi}{2m+1}=-\dfrac{1}{2}$
が成り立つことを証明して下さい。
福田の数学〜慶應義塾大学看護医療学部2025第1問(4)〜三角関数の最大
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
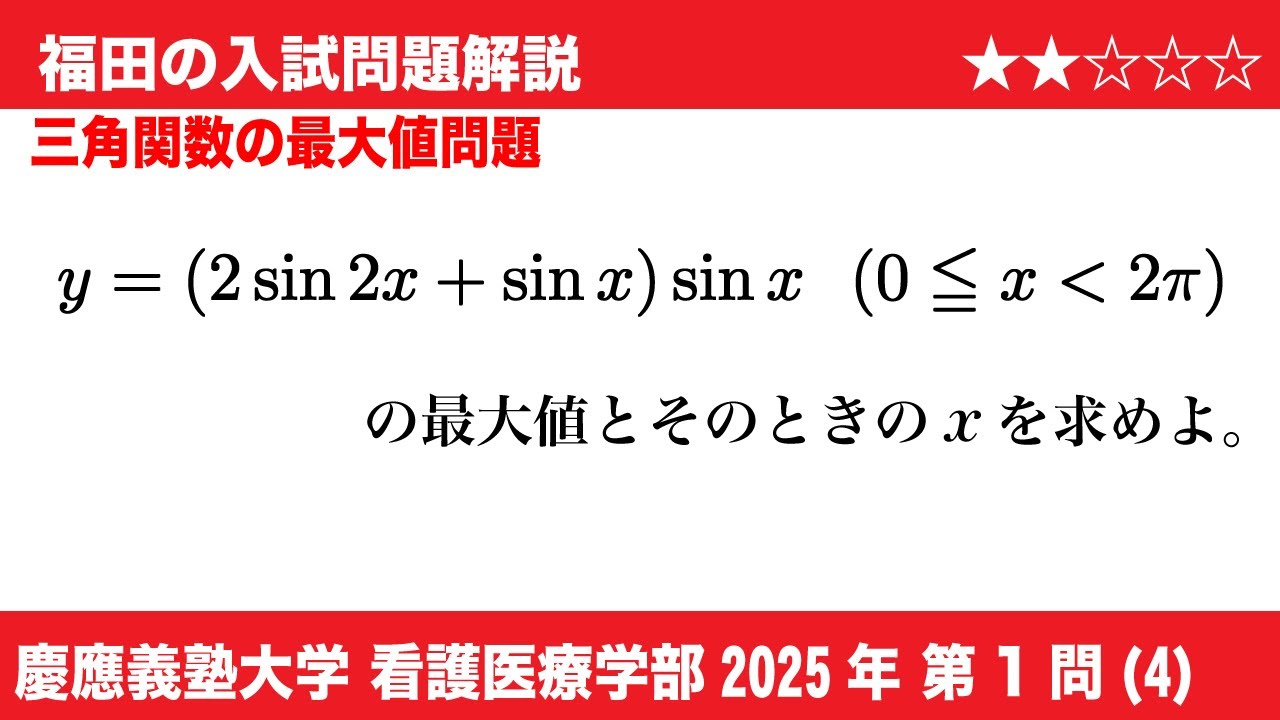
(4)関数$y=(2\sin 2x+\sin x)+\sin x (0\leqq x \lt 2\pi)$は、
$x=\boxed{オ}$のとき最大値$\boxed{カ}$をとる。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(4)関数$y=(2\sin 2x+\sin x)+\sin x (0\leqq x \lt 2\pi)$は、
$x=\boxed{オ}$のとき最大値$\boxed{カ}$をとる。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学480〜三角関数の不等式の証明とイェンゼンの不等式

単元:
#数Ⅱ#式と証明#三角関数#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0\leqq \alpha,\beta \gamma \lt 90°$
$\sin \alpha +\sin \beta +\sin \gamma =1$のとき
$\tan^2\alpha+\tan^2\beta+\tan^2\gamma \geqq\dfrac{3}{8}$
を証明して下さい。
この動画を見る
$0\leqq \alpha,\beta \gamma \lt 90°$
$\sin \alpha +\sin \beta +\sin \gamma =1$のとき
$\tan^2\alpha+\tan^2\beta+\tan^2\gamma \geqq\dfrac{3}{8}$
を証明して下さい。
福田のおもしろ数学460〜三角関数の変形

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
式の変形だけで
$\sin^3 18° + \sin^18°=\dfrac{1}{8}$
を証明して下さい。
*$\sin18°$の値は求めないで!
この動画を見る
式の変形だけで
$\sin^3 18° + \sin^18°=\dfrac{1}{8}$
を証明して下さい。
*$\sin18°$の値は求めないで!
【数Ⅱ】【三角関数】三角関数の合成7 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値, 最小値と, そのときのxの値も求めよ。
y=2(sinx+cosx)+2sinxcosx+1 (0$\leqq$x$\lt$2π)
この動画を見る
次の関数の最大値, 最小値と, そのときのxの値も求めよ。
y=2(sinx+cosx)+2sinxcosx+1 (0$\leqq$x$\lt$2π)
【数Ⅱ】【三角関数】三角関数の合成6 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 y=asinx+bcosxはx=$\frac{π}{6}$で最大値をとり, また, 最小値 -5である。定数a,bの値を求めよ。
この動画を見る
関数 y=asinx+bcosxはx=$\frac{π}{6}$で最大値をとり, また, 最小値 -5である。定数a,bの値を求めよ。
【数Ⅱ】【三角関数】三角関数の合成5 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値, 最小値と, そのときのxの値も求めよ。
y=2sin$^{2}$x+2$\sqrt{3}$sinxcosx+4cos$^{2}$x (0$\leqq$x$\lt$2π)
この動画を見る
次の関数の最大値, 最小値と, そのときのxの値も求めよ。
y=2sin$^{2}$x+2$\sqrt{3}$sinxcosx+4cos$^{2}$x (0$\leqq$x$\lt$2π)
【数Ⅱ】【三角関数】三角関数の合成4 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0$\leqq$x$\leqq$πのとき、次の関数の最大値, 最小値を求めよ。(1)については、そのときのxの値も求めよ。
(1) y=sinx+$\sqrt{3}$cosx
(2) y=2sinx+cosx
この動画を見る
0$\leqq$x$\leqq$πのとき、次の関数の最大値, 最小値を求めよ。(1)については、そのときのxの値も求めよ。
(1) y=sinx+$\sqrt{3}$cosx
(2) y=2sinx+cosx
【数Ⅱ】【三角関数】三角関数の合成3 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値, 最小値を求めよ。(1),(2)については、そのときのxの値も求めよ。
(1) y=-sinx+cosx(0$\leqq$x$\lt$2π)
(2) y=sin2x-$\sqrt{3}$cos2x(0$\leqq$x$\lt$π)
(3) y=4sinx+3cosx
(4) y=$\sqrt{7}$sinx-3cosx
この動画を見る
次の関数の最大値, 最小値を求めよ。(1),(2)については、そのときのxの値も求めよ。
(1) y=-sinx+cosx(0$\leqq$x$\lt$2π)
(2) y=sin2x-$\sqrt{3}$cos2x(0$\leqq$x$\lt$π)
(3) y=4sinx+3cosx
(4) y=$\sqrt{7}$sinx-3cosx
【数Ⅱ】【三角関数】三角関数の合成2 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0$\leqq$x$\lt$2πのとき、次の不等式を解け。
(1) sinx+cosx$\geqq$$\frac{1}{\sqrt{2} }$
(2) cosx$\lt$$\sqrt{3}$sinx
(3) $\sqrt{2}$$\leqq$sinx-$\sqrt{3}$cosx$\lt$$\sqrt{3}$
この動画を見る
0$\leqq$x$\lt$2πのとき、次の不等式を解け。
(1) sinx+cosx$\geqq$$\frac{1}{\sqrt{2} }$
(2) cosx$\lt$$\sqrt{3}$sinx
(3) $\sqrt{2}$$\leqq$sinx-$\sqrt{3}$cosx$\lt$$\sqrt{3}$
【数Ⅱ】【三角関数】三角関数の合成1 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0$\leqq$x$\lt$2πのとき、次の方程式を解け。
(1) $sinx+\sqrt{3}cosx=-1$
(2) $2(sinx-cosx)=\sqrt{6}$
(3) $\sqrt{3}sin2x-cos2x=-\sqrt{2}$
この動画を見る
0$\leqq$x$\lt$2πのとき、次の方程式を解け。
(1) $sinx+\sqrt{3}cosx=-1$
(2) $2(sinx-cosx)=\sqrt{6}$
(3) $\sqrt{3}sin2x-cos2x=-\sqrt{2}$
【数Ⅱ】【三角関数】加法定理の応用7 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
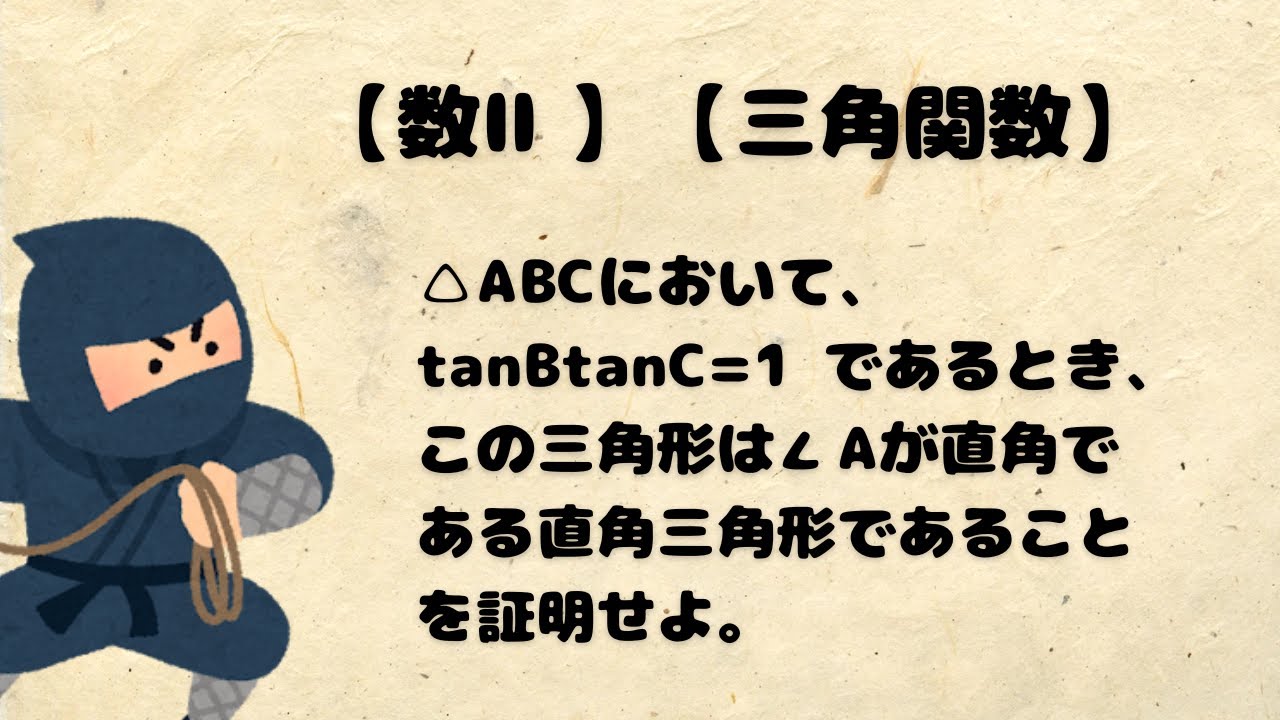
△ABCにおいて、 tanBtanC=1 であるとき、この三角形は∠Aが直角である直角三角形であることを証明せよ。
この動画を見る
△ABCにおいて、 tanBtanC=1 であるとき、この三角形は∠Aが直角である直角三角形であることを証明せよ。
【数Ⅱ】【三角関数】加法定理の応用6 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
この動画を見る
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
【数Ⅱ】【三角関数】加法定理の応用5 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
この動画を見る
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
【数Ⅱ】【三角関数】加法定理の応用4 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
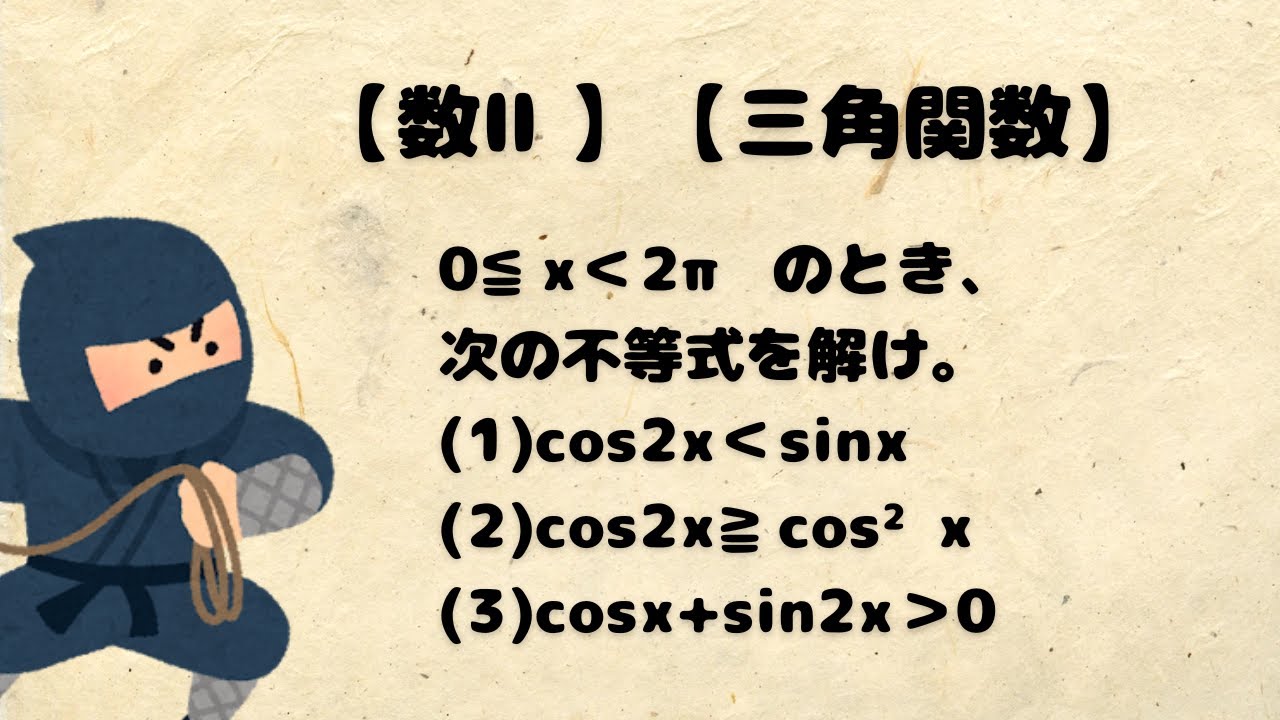
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
この動画を見る
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
【数Ⅱ】【三角関数】加法定理の応用3 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
この動画を見る
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
【数Ⅱ】【三角関数】加法定理の応用2 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
この動画を見る
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
【数Ⅱ】【三角関数】加法定理の応用1 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
この動画を見る
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
福田のおもしろ数学431〜sin^318°+sin^218°の値を求める

福田のおもしろ数学404〜単位円に内接する三角形に関する三角関数の値
単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
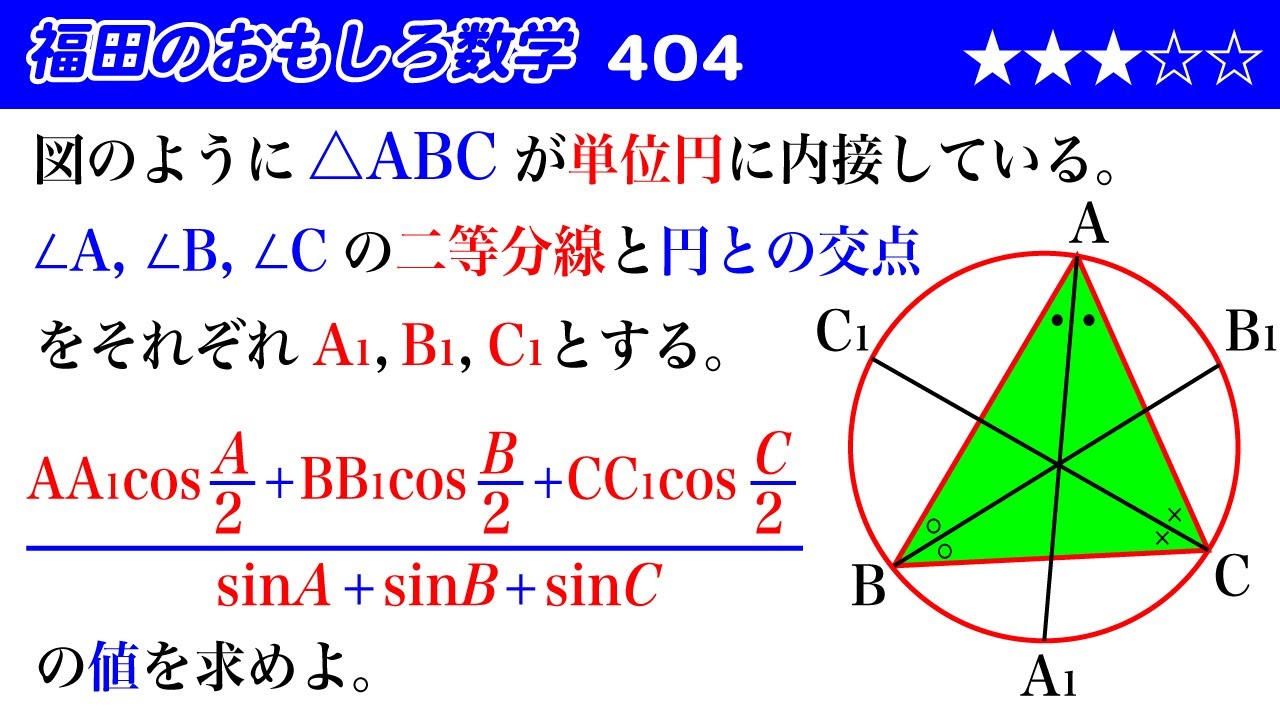
図のように$\triangle ABC$が単位円に内接している。
$\angle A,\angle B,\angle C$の二等分線と円との交点
をそれぞれ$A_1,B_1,C_1$とする。
$\dfrac{AA_1 \cos \dfrac{A}{2}+BB_1\cos\dfrac{B}{2}+CC_1\cos\dfrac{C}{2}}{\sin A+\sin B+\sin C}$
の値を求めよ。
この動画を見る
図のように$\triangle ABC$が単位円に内接している。
$\angle A,\angle B,\angle C$の二等分線と円との交点
をそれぞれ$A_1,B_1,C_1$とする。
$\dfrac{AA_1 \cos \dfrac{A}{2}+BB_1\cos\dfrac{B}{2}+CC_1\cos\dfrac{C}{2}}{\sin A+\sin B+\sin C}$
の値を求めよ。
