三角関数
三角関数
福田の数学〜早稲田大学2021年理工学部第１問〜２直線のなす角の最小
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#微分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ $xy$平面上の曲線$y=x^3$を$C$とする。$C$上の2点$A(-1,-1), B(1,1)$をとる。
さらに、$C$上で原点$O$と$B$の間に動点$P(t,t^3)(0 \lt t \lt 1)$をとる。このとき、
以下の問いに答えよ。
(1)直線$AP$と$x$軸のなす角を$\alpha$とし、直線$PB$と$x$軸のなす角を$\beta$とするとき、
$\tan\alpha,\tan\beta$を$t$を用いて表せ。ただし、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2},\ 0 \lt \beta \lt \displaystyle \frac{\pi}{2}$とする。
(2)$\tan\angle APB$を$t$を用いて表せ。
(3)$\angle APB$を最小にする$t$の値を求めよ。
2021早稲田大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$ $xy$平面上の曲線$y=x^3$を$C$とする。$C$上の2点$A(-1,-1), B(1,1)$をとる。
さらに、$C$上で原点$O$と$B$の間に動点$P(t,t^3)(0 \lt t \lt 1)$をとる。このとき、
以下の問いに答えよ。
(1)直線$AP$と$x$軸のなす角を$\alpha$とし、直線$PB$と$x$軸のなす角を$\beta$とするとき、
$\tan\alpha,\tan\beta$を$t$を用いて表せ。ただし、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2},\ 0 \lt \beta \lt \displaystyle \frac{\pi}{2}$とする。
(2)$\tan\angle APB$を$t$を用いて表せ。
(3)$\angle APB$を最小にする$t$の値を求めよ。
2021早稲田大学理工学部過去問
加法定理の証明をベクトルで
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =
この動画を見る
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =
【行列ができる！】証明：三角関数の加法定理～全国入試問題解法
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
三角関数における加法定理の証明
【回転変換の解説付き！】
$\sin (a \pmβ)=\sin a \cos β \pm \cos a \sin β$
$\cos (a \pmβ)= \cos a \cos β \mp \sin a \sinβ$
この動画を見る
三角関数における加法定理の証明
【回転変換の解説付き！】
$\sin (a \pmβ)=\sin a \cos β \pm \cos a \sin β$
$\cos (a \pmβ)= \cos a \cos β \mp \sin a \sinβ$
【高校数学】三角関数の最初～一般角と弧度法について～ 4-1【数学Ⅱ】
15和歌山県教員採用試験（数学：2番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$0\leqq x\leqq \dfrac{\pi}{2}$とする.
$y=\dfrac{1}{2-\sin^2x}\dfrac{1}{2-\cos^2x}$の
最大値,最小値を求めよ.
この動画を見る
$\boxed{2}$
$0\leqq x\leqq \dfrac{\pi}{2}$とする.
$y=\dfrac{1}{2-\sin^2x}\dfrac{1}{2-\cos^2x}$の
最大値,最小値を求めよ.
数学「大学入試良問集」【8−2 三角関数の解の個数】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
関数$f(\theta)=a(\sqrt{ 3 }\ \sin\theta+\cos\theta)+\sin\theta(\sin\theta+\sqrt{ 3 }\ \cos\theta)$について、次の各問いに答えよ。
ただし、$0 \leqq x \leqq \pi$とする。
（1）$t=\sqrt{ 3 }\ \sin\theta+\cos\theta$のグラフをかけ。
（2）$\sin\theta(\sin\theta+\sqrt{ 3 }\ \cos\theta)$を$t$を用いて表せ。
（3）方程式$f(\theta)=0$が相異なる3つの解をもつときの$a$の値の範囲を求めよ。
この動画を見る
関数$f(\theta)=a(\sqrt{ 3 }\ \sin\theta+\cos\theta)+\sin\theta(\sin\theta+\sqrt{ 3 }\ \cos\theta)$について、次の各問いに答えよ。
ただし、$0 \leqq x \leqq \pi$とする。
（1）$t=\sqrt{ 3 }\ \sin\theta+\cos\theta$のグラフをかけ。
（2）$\sin\theta(\sin\theta+\sqrt{ 3 }\ \cos\theta)$を$t$を用いて表せ。
（3）方程式$f(\theta)=0$が相異なる3つの解をもつときの$a$の値の範囲を求めよ。
数学「大学入試良問集」【8−3 2直線のなす角】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$x$を正の実数とする。
座標平面上の3点$A(0,1),B(0,2),P(x,x)$をとり、$\triangle ABC$を考える。
$x$の値が変化するとき、$\angle APB$の最大値を求めよ。
この動画を見る
$x$を正の実数とする。
座標平面上の3点$A(0,1),B(0,2),P(x,x)$をとり、$\triangle ABC$を考える。
$x$の値が変化するとき、$\angle APB$の最大値を求めよ。
数学「大学入試良問集」【8−1 三角関数の最大・最小】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学#関西大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
次の問いに答えよ。
（1）
$0 \leqq x \leqq 2\pi$のとき、関数
$y=\sin^2x+\sqrt{ 3 }\ \sin\ x\ \cos\ x-2\cos^2x$の最大値と最小値、および、そのときの$x$の値を求めよ。
（2）
点$(x,y)$が原点を中心とする半径1の円周上を動くとき、$xy(x+y-1)$の最大値と最小値を求めよ。
この動画を見る
次の問いに答えよ。
（1）
$0 \leqq x \leqq 2\pi$のとき、関数
$y=\sin^2x+\sqrt{ 3 }\ \sin\ x\ \cos\ x-2\cos^2x$の最大値と最小値、および、そのときの$x$の値を求めよ。
（2）
点$(x,y)$が原点を中心とする半径1の円周上を動くとき、$xy(x+y-1)$の最大値と最小値を求めよ。
2倍角の公式
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
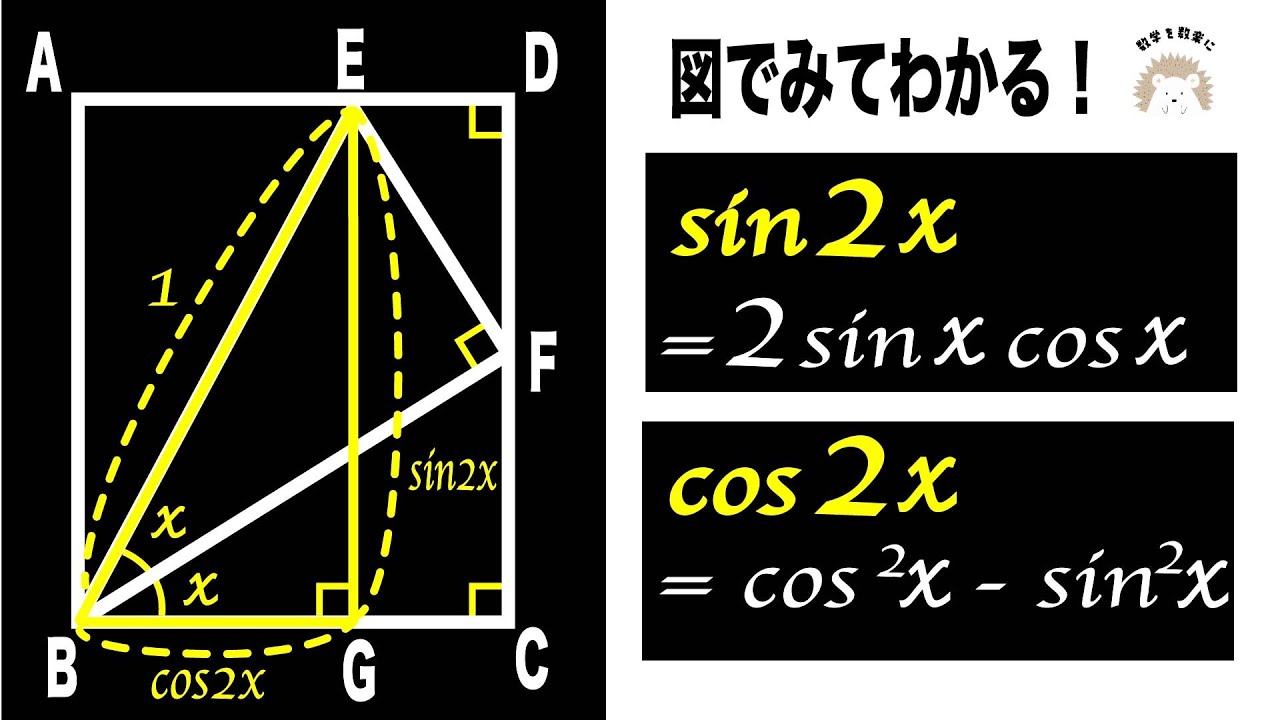
$sin2x=2sinxcosx$
$cos2x=cos^2x-sin^2x$
＊図は動画内参照
この動画を見る
$sin2x=2sinxcosx$
$cos2x=cos^2x-sin^2x$
＊図は動画内参照
ドモアブルの定理の証明と応用
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$は整数である.
$Z=\sin\theta+i\cos\theta$
$Z^n$を$\cos n\theta$と$\sin n\theta$を用いて表せ.
2021京都工芸大過去問
この動画を見る
$n$は整数である.
$Z=\sin\theta+i\cos\theta$
$Z^n$を$\cos n\theta$と$\sin n\theta$を用いて表せ.
2021京都工芸大過去問
綺麗な問題
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
次の値を求めよ.
$\cos\dfrac{\pi}{33}・\cos\dfrac{2\pi}{33}・\cos\dfrac{4\pi}{33}・\cos\dfrac{8\pi}{33}・\cos\dfrac{16\pi}{33}$
この動画を見る
次の値を求めよ.
$\cos\dfrac{\pi}{33}・\cos\dfrac{2\pi}{33}・\cos\dfrac{4\pi}{33}・\cos\dfrac{8\pi}{33}・\cos\dfrac{16\pi}{33}$
コメント欄の別解は本当にありがたいです
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$16^{\cos^2 x}+16^{\sin^2 x}=10$の別解に関して解説していきます.
この動画を見る
$16^{\cos^2 x}+16^{\sin^2 x}=10$の別解に関して解説していきます.
【数Ⅱ】三角関数：解が三角関数で表される2次方程式：p＞0とする。xの方程式4x²+2(1-p)x-p=0の解が、sinθとcosθ(0≦θ＜2π)であるとき、pとθの値を求めよう。
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
解が三角関数で表される2次方程式：p>0とする。xの方程式$4x^2+2(1-p)x-p=0$の解が、$sinθ$と$cosθ(0≦θ＜2\pi)$であるとき、$p$と$\theta$の値を求めよう。
この動画を見る
解が三角関数で表される2次方程式：p>0とする。xの方程式$4x^2+2(1-p)x-p=0$の解が、$sinθ$と$cosθ(0≦θ＜2\pi)$であるとき、$p$と$\theta$の値を求めよう。
2021東大 円と３次関数の共有点
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=ax^3-2x$と原点が中心で半径$1$の円と$6$つの共有点をもつ$a$の範囲を求めよ.$(a\gt 0)$
2021東大過去問
この動画を見る
$y=ax^3-2x$と原点が中心で半径$1$の円と$6$つの共有点をもつ$a$の範囲を求めよ.$(a\gt 0)$
2021東大過去問
【数Ⅱ】三角関数：関数y=-sin²θ+cosθ(0≦θ＜2π)の最大値と最小値を求めよう。その時のθも求めよう。
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数$y=-\sin^2\theta+\cos\theta(0≦\theta＜2\pi)$の最大値と最小値を求めよう。その時の$\theta$も求めよう。
この動画を見る
関数$y=-\sin^2\theta+\cos\theta(0≦\theta＜2\pi)$の最大値と最小値を求めよう。その時の$\theta$も求めよう。
産業医科大 cos sin 和の値
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=\Box$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=\Box$
2019産業医大過去問
この動画を見る
これを解け.
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=\Box$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=\Box$
2019産業医大過去問
練習問題19 教採問題集 （三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$a\gt 0$とする.
$A(0,1),B(0,2),P(a,0)$とし,
$\theta=\angle APB$とする.
(1)$\cos\theta$を$a$で表せ.
(2)$\theta$が最大になる$a$を求めよ.
この動画を見る
$a\gt 0$とする.
$A(0,1),B(0,2),P(a,0)$とし,
$\theta=\angle APB$とする.
(1)$\cos\theta$を$a$で表せ.
(2)$\theta$が最大になる$a$を求めよ.
コメント欄はありがたい。本当に2秒で答えが出た
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
この動画を見る
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
横浜市立（医）tanの半角
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
この動画を見る
$\dfrac{1}{\tan\dfrac{\pi}{24}}$の値を求めよ.
2019横浜市立(医)過去問
札幌医科大2021 三角関数 複数解法
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\triangle ABC$で$\sin C=2\cos A\sin B$である.
$\triangle ABC$の形を求めよ.
2021札幌医大過去問
この動画を見る
$\triangle ABC$で$\sin C=2\cos A\sin B$である.
$\triangle ABC$の形を求めよ.
2021札幌医大過去問
12岡山県教員採用試験（数学：1 5 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(5)$
$2\cos2x-3\sin x-1=0$の解$\alpha,\beta$は
$0\leqq\alpha\lt\beta\leqq \pi$とする.
$\sin(\beta-\alpha)$を求めよ.
この動画を見る
$\boxed{1}-(5)$
$2\cos2x-3\sin x-1=0$の解$\alpha,\beta$は
$0\leqq\alpha\lt\beta\leqq \pi$とする.
$\sin(\beta-\alpha)$を求めよ.
06愛知県教員採用試験（数学：1番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$0\leqq \theta \leqq \dfrac{\pi}{6}$とする.
$\cos\theta+k\sin\theta=k-1$が解をもつとき,
$k$の値を求めよ.
この動画を見る
$\boxed{1}$
$0\leqq \theta \leqq \dfrac{\pi}{6}$とする.
$\cos\theta+k\sin\theta=k-1$が解をもつとき,
$k$の値を求めよ.
cosの積 華麗な解法で綺麗な答え
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\displaystyle \prod_{k=1}^7 \cos\dfrac{\pi}{15}\pi=$
$\cos\dfrac{\pi}{15}\cos\dfrac{2\pi}{15}\cos\dfrac{3\pi}{15}\cos\dfrac{4\pi}{15}\cos\dfrac{5\pi}{15}\cos\dfrac{6\pi}{15}\cos\dfrac{7\pi}{15}$
この動画を見る
これを解け.
$\displaystyle \prod_{k=1}^7 \cos\dfrac{\pi}{15}\pi=$
$\cos\dfrac{\pi}{15}\cos\dfrac{2\pi}{15}\cos\dfrac{3\pi}{15}\cos\dfrac{4\pi}{15}\cos\dfrac{5\pi}{15}\cos\dfrac{6\pi}{15}\cos\dfrac{7\pi}{15}$
16愛知県教員採用試験（数学：5番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$0\leqq x\leqq \pi$とする.
$\sin 2x-2(\sin x+\cos x)-k=0$の
実数解の個数を調べよ.
この動画を見る
$\boxed{3}$
$0\leqq x\leqq \pi$とする.
$\sin 2x-2(\sin x+\cos x)-k=0$の
実数解の個数を調べよ.
30度 45度 60度の直線の式 A 慶應義塾 2021
単元：
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
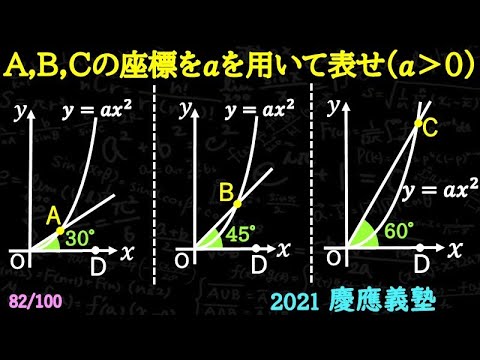
A,B,Cの座標をaを用いて表せ
＊図は動画内参照
2021慶應義塾高等学校
この動画を見る
A,B,Cの座標をaを用いて表せ
＊図は動画内参照
2021慶應義塾高等学校
15愛知県教員採用試験（数学：6番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
$\left(\sin\theta+\dfrac{1}{2}\right)^2+\left(\cos\theta+\dfrac{1}{2}\right)^2=2$のとき,
$\sin\theta,\cos\theta$を解にもつ二次方程式も1つを求めよ.
この動画を見る
$\boxed{6}$
$\left(\sin\theta+\dfrac{1}{2}\right)^2+\left(\cos\theta+\dfrac{1}{2}\right)^2=2$のとき,
$\sin\theta,\cos\theta$を解にもつ二次方程式も1つを求めよ.
14愛知県教員採用試験（数学：5番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$
$\sin3\theta+\sqrt 3\cos3\theta=\sqrt2$を解け.
この動画を見る
$\boxed{5}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$
$\sin3\theta+\sqrt 3\cos3\theta=\sqrt2$を解け.
約束記号 C 慶應義塾 2021
単元：
#数学(中学生)#数Ⅱ#三角関数#加法定理とその応用#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
この動画を見る
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
07大阪府教員採用試験（数学：1番 三角関数と極限）
単元：
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
この動画を見る
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
17愛知県教員採用試験（数学：2番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$y=\cos2\theta+4k\ \sin\theta+3k-3$
任意の定数$theta$に対して$y\leqq 0$となる.
$k$の範囲を求めよ.
この動画を見る
$\boxed{2}$
$y=\cos2\theta+4k\ \sin\theta+3k-3$
任意の定数$theta$に対して$y\leqq 0$となる.
$k$の範囲を求めよ.