三角関数
三角関数
東京海洋大学 三角関数 最大最小 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#東京海洋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
この動画を見る
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
福田の一夜漬け数学〜折れ線の最小(4)〜受験編、一橋大学の問題に挑戦！
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 点$O$を中心とする半径$r$の円周上に、2点$A,B$を$\angle AOB \lt \displaystyle \frac{\pi}{2}$となる
ようにとり、$\theta=\angle AOB$とおく。線分$AB$上に点$D$をとる。また、
点$P$は線分$OA$上を、点$Q$は線分$OB$上を動く。
(1)$a=OD$とおく。$DP+PQ+QD$の最小値を$a$と$\theta$で表せ。
(2)さらに点$D$が線分$AB$上を動くときの
$DP+PQ+QD$の最小値を$r$と$\theta$で表せ。
一橋大学過去問
この動画を見る
${\Large\boxed{1}}$ 点$O$を中心とする半径$r$の円周上に、2点$A,B$を$\angle AOB \lt \displaystyle \frac{\pi}{2}$となる
ようにとり、$\theta=\angle AOB$とおく。線分$AB$上に点$D$をとる。また、
点$P$は線分$OA$上を、点$Q$は線分$OB$上を動く。
(1)$a=OD$とおく。$DP+PQ+QD$の最小値を$a$と$\theta$で表せ。
(2)さらに点$D$が線分$AB$上を動くときの
$DP+PQ+QD$の最小値を$r$と$\theta$で表せ。
一橋大学過去問
和歌山大 三項間漸化式 半角の公式 高校数学 Japanese university entrance exam questions
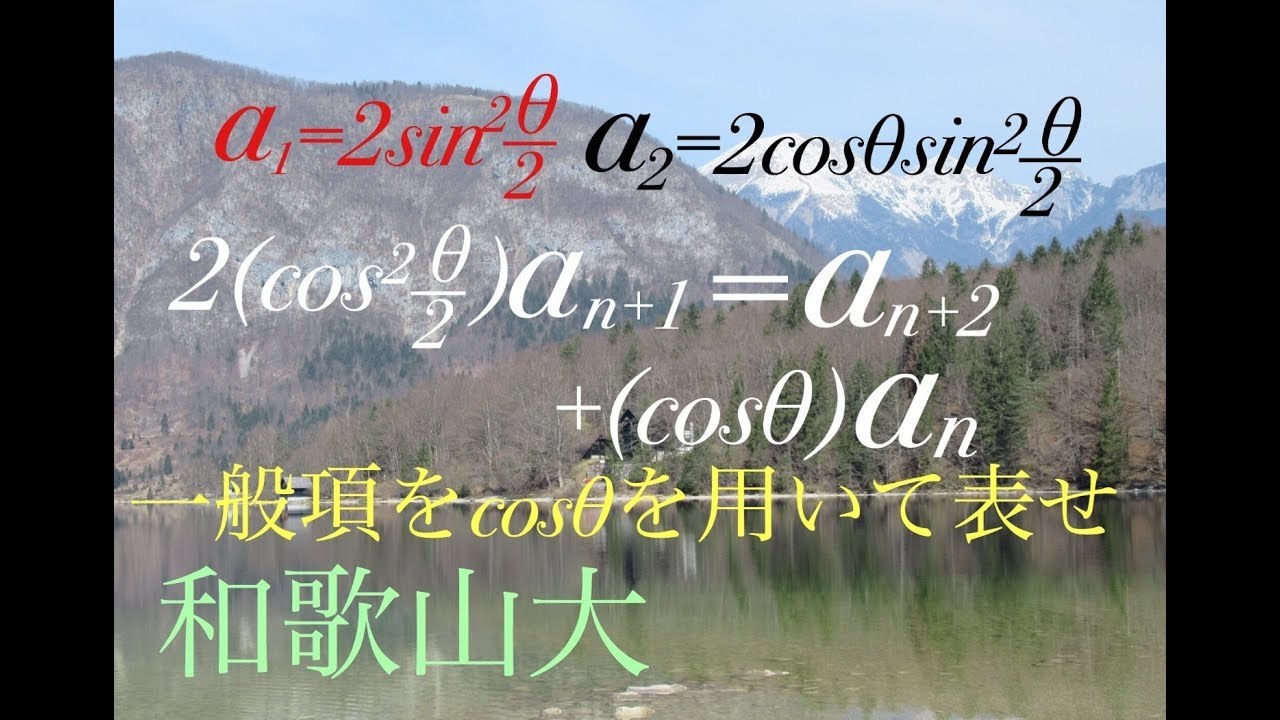
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#三角関数#三角関数とグラフ#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#和歌山大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
この動画を見る
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
慶應（医）空間 直線＆平面の方程式 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#三角関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#慶應義塾大学#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
慶応義塾大学過去問題
直線 $l:6-x=\frac{y+5}{2}=2-z$と
平面$α:z+y-z-1=0$
(1)lとαの交点の座標
(2)lを含み平面αに垂直な平面πの方程式
(3)lと、平面αとπの交線のなす角をθ(0°$\leqq$θ$\leqq$90°)
cosθの値
この動画を見る
慶応義塾大学過去問題
直線 $l:6-x=\frac{y+5}{2}=2-z$と
平面$α:z+y-z-1=0$
(1)lとαの交点の座標
(2)lを含み平面αに垂直な平面πの方程式
(3)lと、平面αとπの交線のなす角をθ(0°$\leqq$θ$\leqq$90°)
cosθの値
九州大学 三倍角 高校数学 Japanese university entrance exam questions
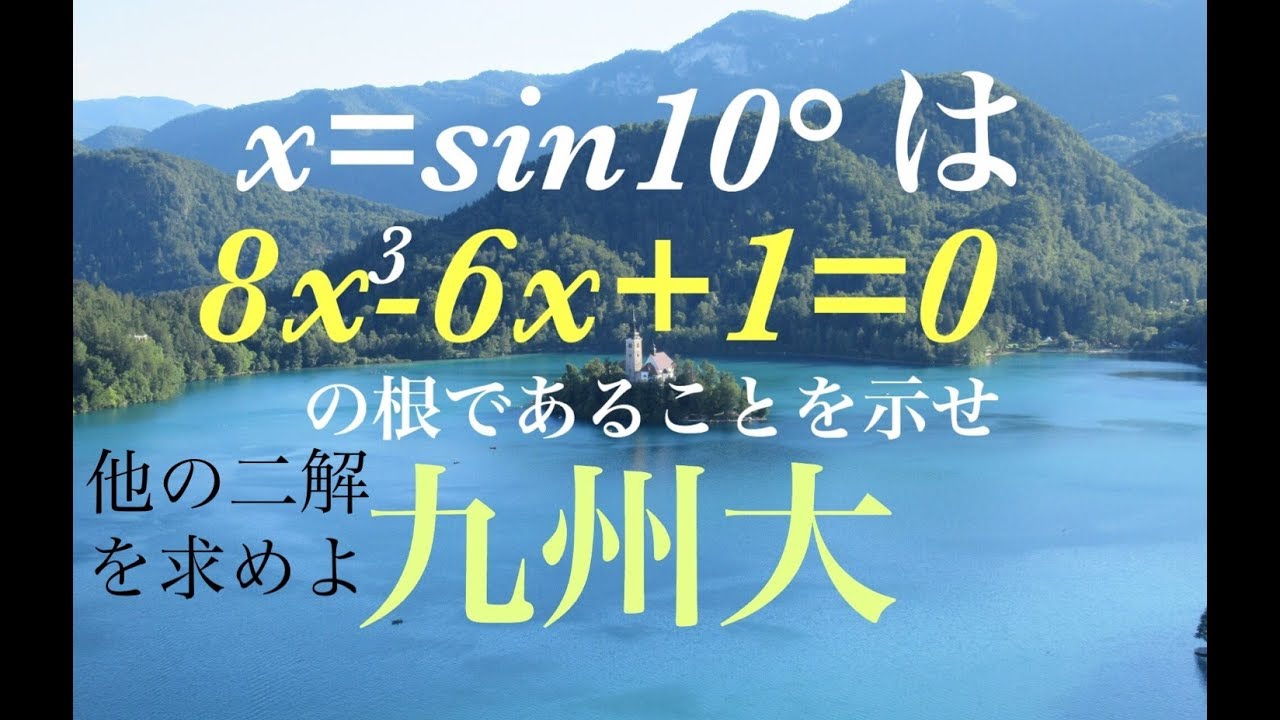
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
九州大学過去問題
(1)$\sin10^{\circ}$は3次方程式$8x^3-6x+1=0$の解であることを示せ。
(2)他の2解を求めよ。
この動画を見る
九州大学過去問題
(1)$\sin10^{\circ}$は3次方程式$8x^3-6x+1=0$の解であることを示せ。
(2)他の2解を求めよ。
【高校数学】数Ⅲ-97 三角関数の導関数②
単元：
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の関数を微分せよ。
①$y=\sin 2 x \cos x$
②$y=\sqrt{1+\sin x}$
③$y=\dfrac{x}{\sin x}$
④$y=\cos^3 2x$
⑤$y=\dfrac{\sin x}{\sin x+\cos x}$
⑥$y=\dfrac{1}{\sin x \cos x}$
この動画を見る
次の関数を微分せよ。
①$y=\sin 2 x \cos x$
②$y=\sqrt{1+\sin x}$
③$y=\dfrac{x}{\sin x}$
④$y=\cos^3 2x$
⑤$y=\dfrac{\sin x}{\sin x+\cos x}$
⑥$y=\dfrac{1}{\sin x \cos x}$
【高校数学】数Ⅲ-96 三角関数の導関数①
単元：
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$(\sin x)'= ①$
$(\cos x)'= ②$
$(\tan x)'= ③$
次の関数を微分せよ。
④$y=\sin 2x$
⑤$y=\cos (3x+2)$
⑥$y=\tan^2 x$
⑦$y=x \cos x$
⑧$y=\sin(x^2+3)$
⑨$y=\cos\dfrac{1}{x}$
この動画を見る
$(\sin x)'= ①$
$(\cos x)'= ②$
$(\tan x)'= ③$
次の関数を微分せよ。
④$y=\sin 2x$
⑤$y=\cos (3x+2)$
⑥$y=\tan^2 x$
⑦$y=x \cos x$
⑧$y=\sin(x^2+3)$
⑨$y=\cos\dfrac{1}{x}$
横浜市立(医) 正二十面体 面のなす角 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'94横浜市立大学過去問題
(1)正五角形ABCDEの一辺を1としたときのAD=ACの長さ
(2)正二十面体のとなり合う面のなす角をθとしたときのcosθの値
この動画を見る
'94横浜市立大学過去問題
(1)正五角形ABCDEの一辺を1としたときのAD=ACの長さ
(2)正二十面体のとなり合う面のなす角をθとしたときのcosθの値
福田の一夜漬け数学〜絶対不等式(2)〜受験編
単元：
#数Ⅰ#数Ⅱ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#集合と命題（集合・命題と条件・背理法）#図形と方程式#三角関数#軌跡と領域#三角関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(1)任意の$\theta$に対して、$-2 \leqq x\cos\theta+y\sin\theta \leqq y+1$ が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
(2)任意の角$\alpha,\beta$に対して、$-1 \leqq x^2\cos\alpha+y\sin\beta \leqq 1$が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
この動画を見る
(1)任意の$\theta$に対して、$-2 \leqq x\cos\theta+y\sin\theta \leqq y+1$ が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
(2)任意の角$\alpha,\beta$に対して、$-1 \leqq x^2\cos\alpha+y\sin\beta \leqq 1$が成立するような
点(x,y)の全体からなる領域をxy平面上に図示し、その面積を求めよ。
福田の一夜漬け数学〜多変数関数、１文字固定その２（受験編）
単元：
#数Ⅱ#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\triangle ABC$において次の不等式を示せ。
(1)$\cos A+\cos B+\cos C \leqq \frac{3}{2}$
(2)$\cos A\cos B \cos C \leqq \frac{1}{8}$
この動画を見る
$\triangle ABC$において次の不等式を示せ。
(1)$\cos A+\cos B+\cos C \leqq \frac{3}{2}$
(2)$\cos A\cos B \cos C \leqq \frac{1}{8}$
【高校数学】数Ⅲ-84 三角関数と極限③
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty} \dfrac{\sin x}{x}$
②$\displaystyle \lim_{x\to 0} x^2 \sin \dfrac{1}{x}$
③$\displaystyle \lim_{x\to \infty} x \sin \dfrac{1}{x}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty} \dfrac{\sin x}{x}$
②$\displaystyle \lim_{x\to 0} x^2 \sin \dfrac{1}{x}$
③$\displaystyle \lim_{x\to \infty} x \sin \dfrac{1}{x}$
組立除法、三角関数の合成、視聴者からの質問への返答
単元：
#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#加法定理とその応用#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
組立除法、三角関数の合成、視聴者からの質問への返答です.
\begin{array}{r}
x-α\enclose{longdiv}{ax^3+bx^2+cx+d\phantom{0}} \\[-3pt]
\end{array}
この動画を見る
組立除法、三角関数の合成、視聴者からの質問への返答です.
\begin{array}{r}
x-α\enclose{longdiv}{ax^3+bx^2+cx+d\phantom{0}} \\[-3pt]
\end{array}
【高校数学】数Ⅲ-83 三角関数と極限②
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0} \dfrac{1-\cos x}{x^2}$
②$\displaystyle \lim_{x\to \frac{\pi}{2}} \dfrac{\cos x}{2x-\pi}$
③$\displaystyle \lim_{x\to 0}\dfrac{\cos 3x-\cos 2x}{x^2}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0} \dfrac{1-\cos x}{x^2}$
②$\displaystyle \lim_{x\to \frac{\pi}{2}} \dfrac{\cos x}{2x-\pi}$
③$\displaystyle \lim_{x\to 0}\dfrac{\cos 3x-\cos 2x}{x^2}$
【高校数学】数Ⅲ-82 三角関数と極限①
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0}\dfrac{\sin 3x}{x}$
②$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{2x}$
③$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{\sin 2x}$
④$\displaystyle \lim_{x\to 0}\dfrac{\sin x-\sin 5x}{2x}$
⑤$\displaystyle \lim_{x\to 0}\dfrac{1-\cos 2x}{x^2}$
⑥$\displaystyle \lim_{x\to 0}\dfrac{x\sin x}{1-\cos x}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0}\dfrac{\sin 3x}{x}$
②$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{2x}$
③$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{\sin 2x}$
④$\displaystyle \lim_{x\to 0}\dfrac{\sin x-\sin 5x}{2x}$
⑤$\displaystyle \lim_{x\to 0}\dfrac{1-\cos 2x}{x^2}$
⑥$\displaystyle \lim_{x\to 0}\dfrac{x\sin x}{1-\cos x}$
【数学】３分で和積公式が馬鹿でもわかる考え方
【数学】４分で積和公式が馬鹿でもわかる考え方
弧度法を使う理由
単元：
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#平均変化率・極限・導関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
弧度法を使う理由を解説していきます.
この動画を見る
弧度法を使う理由を解説していきます.
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
この動画を見る
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
【受験対策】数学－関数１２
単元：
#数Ⅰ#数Ⅱ#２次関数#2次関数とグラフ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
この動画を見る
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
【高校数学】 数Ⅱ－１２２ 三角関数の合成⑤
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①関数$y=2\sin x \cos x+\sin x \cos x+1$の最大値と最小値を求めよう。
この動画を見る
①関数$y=2\sin x \cos x+\sin x \cos x+1$の最大値と最小値を求めよう。
【高校数学】 数Ⅱ－１２１ 三角関数の合成④
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$0 \leqq \theta \lt 2π$のとき、関数$y=-\sin \theta +\sqrt{ 3 } \theta$の最大値と最小値、およびそのときの$\theta$の値を求めよう。
②関数$y=\sin x-2\cos x$の最大値と最小値を求めよう。
この動画を見る
①$0 \leqq \theta \lt 2π$のとき、関数$y=-\sin \theta +\sqrt{ 3 } \theta$の最大値と最小値、およびそのときの$\theta$の値を求めよう。
②関数$y=\sin x-2\cos x$の最大値と最小値を求めよう。
【高校数学】 数Ⅱ－１２０ 三角関数の合成③
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$0 \leqq x \lt 2π$のとき、次の不等式を解こう。
①$\sin x-\sqrt{ 3 } \cos x \gt -1 $
②$\sqrt{ 3 } \sin x - \cos x \leqq \sqrt{ 2 }$
この動画を見る
◎$0 \leqq x \lt 2π$のとき、次の不等式を解こう。
①$\sin x-\sqrt{ 3 } \cos x \gt -1 $
②$\sqrt{ 3 } \sin x - \cos x \leqq \sqrt{ 2 }$
【高校数学】 数Ⅱ－１１９ 三角関数の合成②
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$0 \leqq x \lt 2π$のとき、次の方程式を解こう。
①$\sqrt{ 3 } \sin x-\cos x=\sqrt{ 3 } $
②$2(\sin x + \cos x) -\sqrt{ 6 }$
この動画を見る
◎$0 \leqq x \lt 2π$のとき、次の方程式を解こう。
①$\sqrt{ 3 } \sin x-\cos x=\sqrt{ 3 } $
②$2(\sin x + \cos x) -\sqrt{ 6 }$
【高校数学】 数Ⅱ－１１８ 三角関数の合成①
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の式を$rsin(\theta+\alpha)$の形に変形しよう。ただし、$r \gt 0 ,-π \lt \alpha \lt π$とする。
①$\sqrt{ 3 } \sin \theta+\cos \theta$
②$\sqrt{ 2 } \sin \theta-\sqrt{ 6 } \cos \theta$
③$3 \sin \theta+4 \cos \theta$
この動画を見る
◎次の式を$rsin(\theta+\alpha)$の形に変形しよう。ただし、$r \gt 0 ,-π \lt \alpha \lt π$とする。
①$\sqrt{ 3 } \sin \theta+\cos \theta$
②$\sqrt{ 2 } \sin \theta-\sqrt{ 6 } \cos \theta$
③$3 \sin \theta+4 \cos \theta$
【高校数学】 数Ⅱ－１１７ 和と積の公式②・和(差)→積編
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\sin A+\sin B=$①＿＿＿＿＿＿＿＿＿＿＿＿
$\cos A+\cos B=$②＿＿＿＿＿＿＿＿＿＿＿＿
$\sin A-\sin B=$③＿＿＿＿＿＿＿＿＿＿＿＿
$\cos A-\cos B=$④＿＿＿＿＿＿＿＿＿＿＿＿
◎次の値を求めよう。
⑤$\sin 105°+\sin 15°$
⑥$\cos 75°-\sin 15°$
⑦$\cos75°+\cos15°$
この動画を見る
$\sin A+\sin B=$①＿＿＿＿＿＿＿＿＿＿＿＿
$\cos A+\cos B=$②＿＿＿＿＿＿＿＿＿＿＿＿
$\sin A-\sin B=$③＿＿＿＿＿＿＿＿＿＿＿＿
$\cos A-\cos B=$④＿＿＿＿＿＿＿＿＿＿＿＿
◎次の値を求めよう。
⑤$\sin 105°+\sin 15°$
⑥$\cos 75°-\sin 15°$
⑦$\cos75°+\cos15°$
【高校数学】 数Ⅱ－１１５ 三角関数を含む方程式・不等式⑧
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0 \leqq x \lt 2π$のとき、次の不等式を解こう。
①$\cos 2x \leqq 3 \sin x-1$
②$\sin 2x \gt \sin x$
この動画を見る
$0 \leqq x \lt 2π$のとき、次の不等式を解こう。
①$\cos 2x \leqq 3 \sin x-1$
②$\sin 2x \gt \sin x$
【高校数学】 数Ⅱ－１１４ 三角関数を含む方程式・不等式⑦
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0 \leqq x \lt 2π$のとき、次の方程式を書こう。
①$2 \cos 2x+1=4\sin x$
②$\sin2x=\cos x$
この動画を見る
$0 \leqq x \lt 2π$のとき、次の方程式を書こう。
①$2 \cos 2x+1=4\sin x$
②$\sin2x=\cos x$
【高校数学】 数Ⅱ－１１３ 加法定理の応用③・半角の公式編
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\sin^2 \displaystyle \frac{\alpha}{2}=$
②$\cos ^2 \displaystyle \frac{\alpha}{2}=$
③$\tan ^2 \displaystyle \frac{\alpha}{2}=$
◎$\displaystyle \frac{3}{2}π \lt \alpha \lt 2π$で、$\sin \alpha=-\displaystyle \frac{3}{5}$のとき、次の値を求めよう。
④$\sin \displaystyle \frac{\alpha}{2}=$
⑤$\cos \displaystyle \frac{\alpha}{2}=$
⑥$\tan \displaystyle \frac{\alpha}{2}=$
この動画を見る
①$\sin^2 \displaystyle \frac{\alpha}{2}=$
②$\cos ^2 \displaystyle \frac{\alpha}{2}=$
③$\tan ^2 \displaystyle \frac{\alpha}{2}=$
◎$\displaystyle \frac{3}{2}π \lt \alpha \lt 2π$で、$\sin \alpha=-\displaystyle \frac{3}{5}$のとき、次の値を求めよう。
④$\sin \displaystyle \frac{\alpha}{2}=$
⑤$\cos \displaystyle \frac{\alpha}{2}=$
⑥$\tan \displaystyle \frac{\alpha}{2}=$
【高校数学】 数Ⅱ－１１２ 加法定理の応用②・３倍角の公式編
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$sin3\alpha=3\sin\alpha-4\sin^3\alpha$を証明しよう。
②$cos3\alpha=3\cos\alpha-4\cos^3\alpha$を証明しよう。
この動画を見る
①$sin3\alpha=3\sin\alpha-4\sin^3\alpha$を証明しよう。
②$cos3\alpha=3\cos\alpha-4\cos^3\alpha$を証明しよう。
【高校数学】 数Ⅱ－１１１ 加法定理の応用①・２倍角の公式編
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\sin \alpha=$①＿＿＿＿＿＿＿＿
$\cos \alpha=$②＿＿＿＿＿＿=＿＿＿＿＿＿=＿＿＿＿＿＿＿＿
$\tan \alpha=$③＿＿＿＿＿＿＿＿
◎$\displaystyle \frac{π}{2} \lt \alpha \lt π$で、$\sin \alpha=\displaystyle \frac{7}{4}$のとき、次の値を求めよう。
④$\sin 2 \alpha$
⑤$\cos 2 \alpha$
⑥$\tan 2 \alpha$
この動画を見る
$\sin \alpha=$①＿＿＿＿＿＿＿＿
$\cos \alpha=$②＿＿＿＿＿＿=＿＿＿＿＿＿=＿＿＿＿＿＿＿＿
$\tan \alpha=$③＿＿＿＿＿＿＿＿
◎$\displaystyle \frac{π}{2} \lt \alpha \lt π$で、$\sin \alpha=\displaystyle \frac{7}{4}$のとき、次の値を求めよう。
④$\sin 2 \alpha$
⑤$\cos 2 \alpha$
⑥$\tan 2 \alpha$