指数関数
指数関数
 指数関数
指数関数
福田のおもしろ数学552〜(−1)のi乗はいくら?

福田のおもしろ数学514〜指数方程式の解

福田のおもしろ数学511〜50の50乗と49の51乗の大小比較

福田の数学〜立教大学2025経済学部第1問(1)〜指数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(1)$2^{1-3x} \geqq \left(\dfrac{1}{\sqrt2}\right)^x$を満たす
実数$x$の値の範囲は$\boxed{ア}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜慶應義塾大学2025経済学部第4問〜指数不等式と対数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$p$を正の実数、$m$を自然数とし、
曲線$y=-x^2$上の点$(-p,-p^2)$における
接線と直線$y=2m$の交点を$P_m$とする。
$P_m$の$x$座標が$1$以下となる$m$の最大値を
$N$とする。
(1)$P_m$の$x$座標を、$p$と$m$を用いて表せ。
(2)$N=40$が成り立つ$p$の範囲を求めよ。
以下、$n$を自然数とし、
$a=3n\log_3 6-\log_2+n$とする。
(3)$3^a$は$2$以上の自然数である。
$3^a$の素因数分解を、$n$を用いて書け。
(4)$p=3^a$のとき、$N\lt 2^{1000}$となる
自然数$n$の最大値を求めよ。
なお、必要があれば$1.58 \lt \log_2 3 \lt 1.50$を用いよ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{4}$
$p$を正の実数、$m$を自然数とし、
曲線$y=-x^2$上の点$(-p,-p^2)$における
接線と直線$y=2m$の交点を$P_m$とする。
$P_m$の$x$座標が$1$以下となる$m$の最大値を
$N$とする。
(1)$P_m$の$x$座標を、$p$と$m$を用いて表せ。
(2)$N=40$が成り立つ$p$の範囲を求めよ。
以下、$n$を自然数とし、
$a=3n\log_3 6-\log_2+n$とする。
(3)$3^a$は$2$以上の自然数である。
$3^a$の素因数分解を、$n$を用いて書け。
(4)$p=3^a$のとき、$N\lt 2^{1000}$となる
自然数$n$の最大値を求めよ。
なお、必要があれば$1.58 \lt \log_2 3 \lt 1.50$を用いよ。
$2025$年慶應義塾大学経済学部過去問題
福田の数学〜北海道大学2025理系第1問〜指数対数の基本性質と数列

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$\alpha,r$を$\alpha \gt 1,r \gt 1$を満たす実数とする。
数列$\{a_n\}$を$a_1=\alpha$で公比が$r$の等比数列とする。
数列$\{b_n\}$を
$b_n=\log_{a_{n}} (a_{n+1}) (n=1,2,3,\cdots)$で定める。
(1)$b_n$を$n$と$\log_{\alpha}r$を用いて表せ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{1}$
$\alpha,r$を$\alpha \gt 1,r \gt 1$を満たす実数とする。
数列$\{a_n\}$を$a_1=\alpha$で公比が$r$の等比数列とする。
数列$\{b_n\}$を
$b_n=\log_{a_{n}} (a_{n+1}) (n=1,2,3,\cdots)$で定める。
(1)$b_n$を$n$と$\log_{\alpha}r$を用いて表せ。
$2025$年北海道大学理系過去問題
【数Ⅱ】【指数関数と対数関数】指数対数計算5 ※問題文は概要欄

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式の値を求めよ。
(1) $5^{\log_{5} 7}$
(2) $10^{1+\log_{10} 3}$
(3) $36^{\log_6 \sqrt{5}}$
(4) $7^{\log_{49} 4}$
$xyz≠0$, $2^x=5^y=10^{\frac{2}{z}}$のとき、等式$\frac{1}{x}+\frac{1}{y}=\frac{2}{z}$を証明せよ。
$\log_{11} 2$の小数第1位の数を求めよ。
この動画を見る
次の式の値を求めよ。
(1) $5^{\log_{5} 7}$
(2) $10^{1+\log_{10} 3}$
(3) $36^{\log_6 \sqrt{5}}$
(4) $7^{\log_{49} 4}$
$xyz≠0$, $2^x=5^y=10^{\frac{2}{z}}$のとき、等式$\frac{1}{x}+\frac{1}{y}=\frac{2}{z}$を証明せよ。
$\log_{11} 2$の小数第1位の数を求めよ。
【数Ⅱ】【指数関数と対数関数】指数対数計算4 ※問題文は概要欄

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問
次の式の値を求めよ。
$(1)\, 5^{\log_{5}{7}}$
$(2)\, 10^{1+\log_{10}3}$
$(3)\, 36^{\log_{6}{\sqrt{5}}}$
$(4)\, 7^{\log_{49}{4}}$
第2問
$xyz \neq 0,\, 2^{x}=5^{y}=10^{\frac{z}{2}}$ のとき、等式 $\frac{1}{x}+\frac{1}{y}=\frac{2}{z}$ を証明せよ。
第3問
$\log_{11}{2}$ の小数第1位の数を求めよ。
この動画を見る
第1問
次の式の値を求めよ。
$(1)\, 5^{\log_{5}{7}}$
$(2)\, 10^{1+\log_{10}3}$
$(3)\, 36^{\log_{6}{\sqrt{5}}}$
$(4)\, 7^{\log_{49}{4}}$
第2問
$xyz \neq 0,\, 2^{x}=5^{y}=10^{\frac{z}{2}}$ のとき、等式 $\frac{1}{x}+\frac{1}{y}=\frac{2}{z}$ を証明せよ。
第3問
$\log_{11}{2}$ の小数第1位の数を求めよ。
【数Ⅱ】【指数関数と対数関数】対数計算1 ※問題文は概要欄

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を簡単にせよ。
(1) $(\log_{2} 9+\log_{8} 3)(\log_{3} 2+\log_{9} 4)$
(2) $\log_{4} 3・\log_{9} 25・\log_{5} 8)$
(3) $\log_{2} 10・\log_{5} 10-(\log_{2} 5+\log_{5} 2)$
$a=\log_{2} 3$,$b=\log_{2} 5$とするとき、次の式をa,bで表せ。
(1) $\log_{2} 15$
(2) $\log_{2} 75$
(3) $\log_{4} 45$
$p=\log_{a} x$,$q=\log_{a} y$,$r=\log_{a} z$であるとき、次の各式をp,q,rで表せ。
ただし、a,x,y,zは正の数とし、a≠1とする。
(1) $\log_{a} x²y³z⁴$
(2) $\log_{a} \frac{x}{(yz)^2}$
(3) $\log_{a} \frac{x\sqrt{y}}{\sqrt[3]{z}}$
$a=\log_{15} 3$, $b=\log_{3} 2$とするとき、次の式をa,bで表せ。
(1) $\log_{15} 2$
(2) $\log_{15} 5$
この動画を見る
次の式を簡単にせよ。
(1) $(\log_{2} 9+\log_{8} 3)(\log_{3} 2+\log_{9} 4)$
(2) $\log_{4} 3・\log_{9} 25・\log_{5} 8)$
(3) $\log_{2} 10・\log_{5} 10-(\log_{2} 5+\log_{5} 2)$
$a=\log_{2} 3$,$b=\log_{2} 5$とするとき、次の式をa,bで表せ。
(1) $\log_{2} 15$
(2) $\log_{2} 75$
(3) $\log_{4} 45$
$p=\log_{a} x$,$q=\log_{a} y$,$r=\log_{a} z$であるとき、次の各式をp,q,rで表せ。
ただし、a,x,y,zは正の数とし、a≠1とする。
(1) $\log_{a} x²y³z⁴$
(2) $\log_{a} \frac{x}{(yz)^2}$
(3) $\log_{a} \frac{x\sqrt{y}}{\sqrt[3]{z}}$
$a=\log_{15} 3$, $b=\log_{3} 2$とするとき、次の式をa,bで表せ。
(1) $\log_{15} 2$
(2) $\log_{15} 5$
【数Ⅱ】【指数関数と対数関数】指数計算3 ※問題文は概要欄

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ
(1)$y=2^{x+1}$
(2)$y=(\frac{1}{5})^{x-1}$
(3)$y=4・2^x$
(4)$y=3^x-1$
次の数の大小を不等号を用いて表せ
(1)$2^{\frac{1}{2}}$ $3^{\frac{1}{3}}$ $7^{\frac{1}{6}}$
(2)$2^{30}$ $3^{20}$ $10^{10}$
次の方程式,不等式を解け
(1)$4^x+2^{x+1}-24=0$
(2)$10^{2x}+10^x=2$
(3)$9^{x+1}-28・3^x+3=0$
(4)$16^x-3・4^x-4≧0$
(5)${\frac{1}{9}}^x-{\frac{1}{3}}^x-6<0$
(6)${\frac{1}{4}}^{x-1}-9・{\frac{1}{2}}^x+2>0$
次の関数の最大値,最小値があれば,それを求めよまた,そのときのxの値を求めよ
(1)$y=2^{2x}-4・2^x+1$
(2)$y=-4^x+2^x+2$$(-1≦x≦2)$
この動画を見る
次の関数のグラフをかけ
(1)$y=2^{x+1}$
(2)$y=(\frac{1}{5})^{x-1}$
(3)$y=4・2^x$
(4)$y=3^x-1$
次の数の大小を不等号を用いて表せ
(1)$2^{\frac{1}{2}}$ $3^{\frac{1}{3}}$ $7^{\frac{1}{6}}$
(2)$2^{30}$ $3^{20}$ $10^{10}$
次の方程式,不等式を解け
(1)$4^x+2^{x+1}-24=0$
(2)$10^{2x}+10^x=2$
(3)$9^{x+1}-28・3^x+3=0$
(4)$16^x-3・4^x-4≧0$
(5)${\frac{1}{9}}^x-{\frac{1}{3}}^x-6<0$
(6)${\frac{1}{4}}^{x-1}-9・{\frac{1}{2}}^x+2>0$
次の関数の最大値,最小値があれば,それを求めよまた,そのときのxの値を求めよ
(1)$y=2^{2x}-4・2^x+1$
(2)$y=-4^x+2^x+2$$(-1≦x≦2)$
【数Ⅱ】【指数関数と対数関数】指数計算2 ※問題文は概要欄

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a>0, $a^{2x}=5$のとき,$(a^{4x}-a^{-4x})÷(a^x-a^{-x})$の値を求めよ
$2^x-2^{-x}=3$のとき,$2^x+2^{-x}$の値を求めよ
地球と太陽の距離を$1.5×10^{11}$m,光の進む速さを毎秒$3.0×10^8$mとする。
このとき,光が太陽から地球まで到達するには何秒かかるか
この動画を見る
a>0, $a^{2x}=5$のとき,$(a^{4x}-a^{-4x})÷(a^x-a^{-x})$の値を求めよ
$2^x-2^{-x}=3$のとき,$2^x+2^{-x}$の値を求めよ
地球と太陽の距離を$1.5×10^{11}$m,光の進む速さを毎秒$3.0×10^8$mとする。
このとき,光が太陽から地球まで到達するには何秒かかるか
【数Ⅱ】【指数対数】指数計算1 ※問題文は概要欄

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a$\gt$0,b$\gt$0とする。次の式を計算せよ。
(1)(a$^{\frac{1}{2}}$+a$^{\frac{1}{4}}$b$^{\frac{1}{4}}$+b$^{\frac{1}{2}}$)(a$^{\frac{1}{2}}$-a$^{\frac{1}{4}}$b$^{\frac{1}{4}}$+b$^{\frac{1}{2}}$)
(2)(a$^{\frac{x}{3}}$-b$^{-\frac{x}{3}}$)(a$^{\frac{2x}{3}}$+a$^{\frac{x}{3}}$b$^{-\frac{x}{3}}$+b$^{-\frac{2x}{3}}$)
(1)($\sqrt[4]{6}$+$\sqrt[4]{5}$)($\sqrt[4]{6}$-$\sqrt[4]{5}$)
(2)($\sqrt[3]{4}$+$\sqrt[3]{2}$)$^3$+($\sqrt[3]{4}$-$\sqrt[3]{2}$)$^3$
(1) $\sqrt[5]{-32}$
(2) $\sqrt[3]{-\frac{1}{64}}$
(3) $\sqrt[3]{54}$$\times$2$\sqrt[3]{-2}$$\times$$\sqrt[3]{16}$
(4) $\sqrt[3]{-24}$+$\sqrt[3]{81}$)$+$$\sqrt[3]{-3}$
x$^{\frac{1}{3}}$+x$^{-\frac{1}{3}}$=3のとき、x+x$^{-1}$, x$^{3}$+x$^{-3}$の値を求めよ。
この動画を見る
a$\gt$0,b$\gt$0とする。次の式を計算せよ。
(1)(a$^{\frac{1}{2}}$+a$^{\frac{1}{4}}$b$^{\frac{1}{4}}$+b$^{\frac{1}{2}}$)(a$^{\frac{1}{2}}$-a$^{\frac{1}{4}}$b$^{\frac{1}{4}}$+b$^{\frac{1}{2}}$)
(2)(a$^{\frac{x}{3}}$-b$^{-\frac{x}{3}}$)(a$^{\frac{2x}{3}}$+a$^{\frac{x}{3}}$b$^{-\frac{x}{3}}$+b$^{-\frac{2x}{3}}$)
(1)($\sqrt[4]{6}$+$\sqrt[4]{5}$)($\sqrt[4]{6}$-$\sqrt[4]{5}$)
(2)($\sqrt[3]{4}$+$\sqrt[3]{2}$)$^3$+($\sqrt[3]{4}$-$\sqrt[3]{2}$)$^3$
(1) $\sqrt[5]{-32}$
(2) $\sqrt[3]{-\frac{1}{64}}$
(3) $\sqrt[3]{54}$$\times$2$\sqrt[3]{-2}$$\times$$\sqrt[3]{16}$
(4) $\sqrt[3]{-24}$+$\sqrt[3]{81}$)$+$$\sqrt[3]{-3}$
x$^{\frac{1}{3}}$+x$^{-\frac{1}{3}}$=3のとき、x+x$^{-1}$, x$^{3}$+x$^{-3}$の値を求めよ。
福田のおもしろ数学427〜累乗の繰り返しの数と2025の大小比較

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a=\sqrt[2025]{2025}$とする。
$a^{a^{a^{\cdots a}}} \}2025$個と$2025$の大小を比較して下さい。
この動画を見る
$a=\sqrt[2025]{2025}$とする。
$a^{a^{a^{\cdots a}}} \}2025$個と$2025$の大小を比較して下さい。
福田のおもしろ数学354〜指数方程式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。
この動画を見る
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。
319 入れ子になった関数を読み解く:距離を求める関数

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
正の実数 aと 実数 bに対して、べき乗(a, b)はaのb乗を計算して返す関数である。
正の実数x, yに対して、√(xの2乗足すyの2乗)の計算結果を返す関数は次のうちどれか。
1.(べき乗(x,2)+べき乗(y,2))/2
2.べき乗(べき乗(x,2),0.5)+べき乗(べき乗(y,2),0.5)
3.べき乗(べき乗(x,2)+べき乗(y,2),0.5)
4.べき乗(べき乗(x+y,2),0.5)
この動画を見る
正の実数 aと 実数 bに対して、べき乗(a, b)はaのb乗を計算して返す関数である。
正の実数x, yに対して、√(xの2乗足すyの2乗)の計算結果を返す関数は次のうちどれか。
1.(べき乗(x,2)+べき乗(y,2))/2
2.べき乗(べき乗(x,2),0.5)+べき乗(べき乗(y,2),0.5)
3.べき乗(べき乗(x,2)+べき乗(y,2),0.5)
4.べき乗(べき乗(x+y,2),0.5)
大小比較の難問!どう解く?

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
e^πとπ^eの大小を比較せよ。
この動画を見る
e^πとπ^eの大小を比較せよ。
数がでかすぎる!1の位の数字をどう求める?【東京大学】【数学 入試問題】

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(10^210)/(10^10+3)の整数部分のけた数と、1の位の数字を求めよ。ただし、3^21=10460353203を用いてよい。
この動画を見る
(10^210)/(10^10+3)の整数部分のけた数と、1の位の数字を求めよ。ただし、3^21=10460353203を用いてよい。
福田の数学〜上智大学2024TEAP利用型文系第3問(1)〜対数指数不等式と領域に含まれる格子点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
この動画を見る
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
大学入試問題#926「これは合同式使うしかないか」 #産業医科大学2024

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$515^{2024}$の下2桁を求めよ.
2024産業医科大学過去問題
この動画を見る
$515^{2024}$の下2桁を求めよ.
2024産業医科大学過去問題
福田のおもしろ数学245〜3乗根を含む2重根号の計算

福田のおもしろ数学221〜x^y=y^xを解こう

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x^y=y^x \, (x>0, \, y>0)$ を満たす $(x, \, y)$ を求めて下さい。
この動画を見る
$x^y=y^x \, (x>0, \, y>0)$ を満たす $(x, \, y)$ を求めて下さい。
福田のおもしろ数学219〜複雑な指数方程式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{27^x+343^x}{63^x+147^x}=\dfrac{37}{21}$を満たす$x$をすべて求めよ。
この動画を見る
$\dfrac{27^x+343^x}{63^x+147^x}=\dfrac{37}{21}$を満たす$x$をすべて求めよ。
指数方程式 (高校数学)
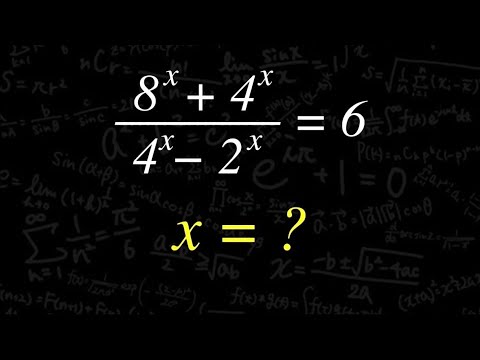
√の中に8がいっぱい!!
単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{8\sqrt{8\sqrt8}}=2$
この動画を見る
$\sqrt{8\sqrt{8\sqrt8}}=2$
√の中に8がいっぱい!!
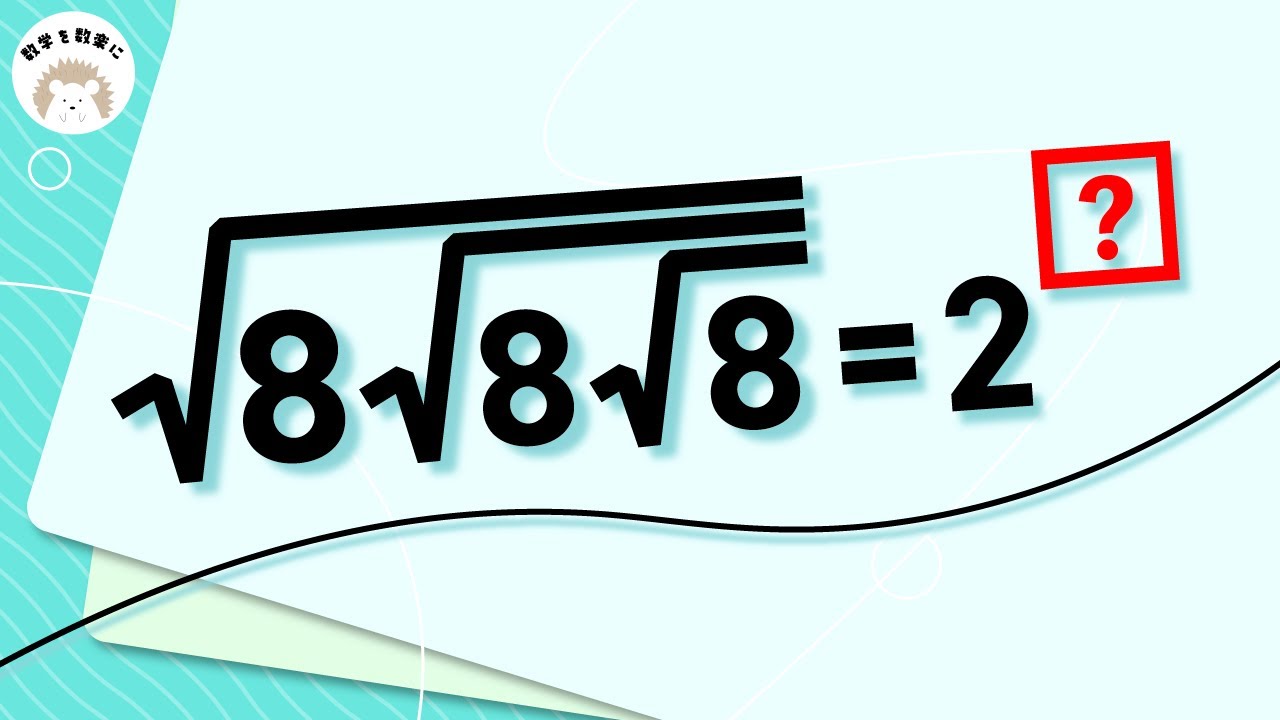
√の中に8がいっぱい!!
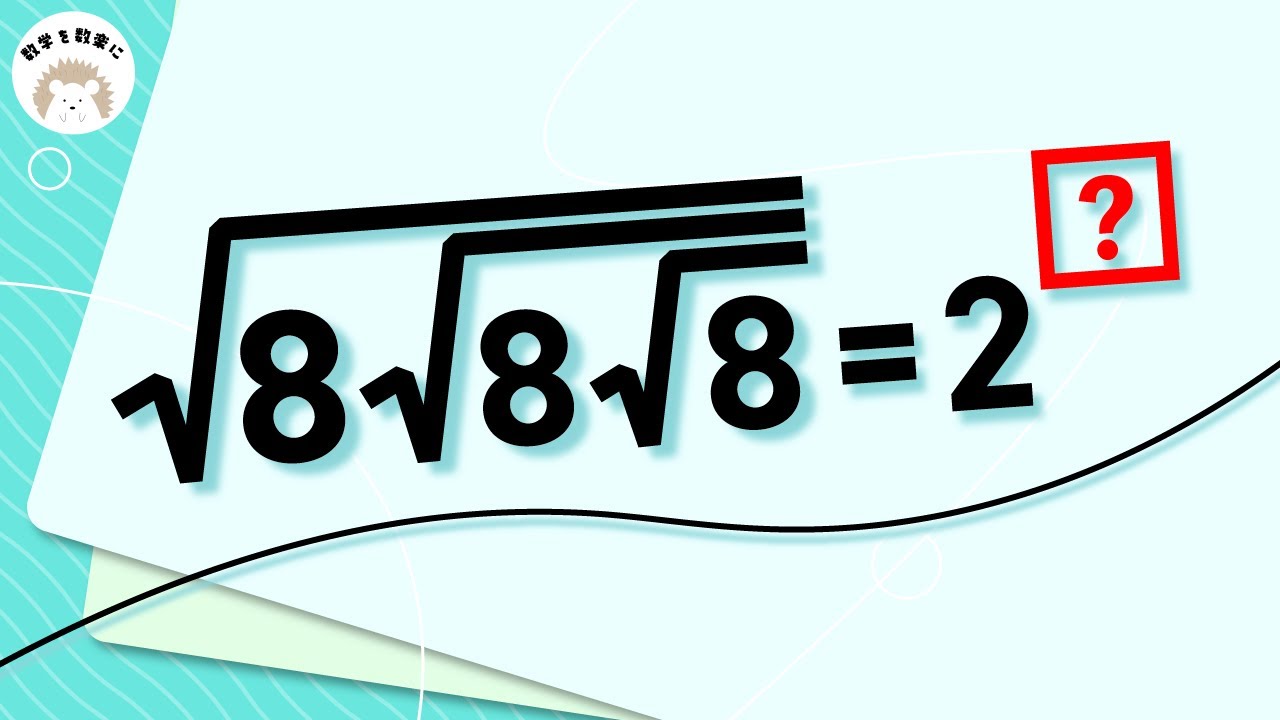
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \sqrt{8\sqrt{8\sqrt{8}}}=2^\boxed{?}$
この動画を見る
$\displaystyle \sqrt{8\sqrt{8\sqrt{8}}}=2^\boxed{?}$
指数連立方程式 (高校数学)
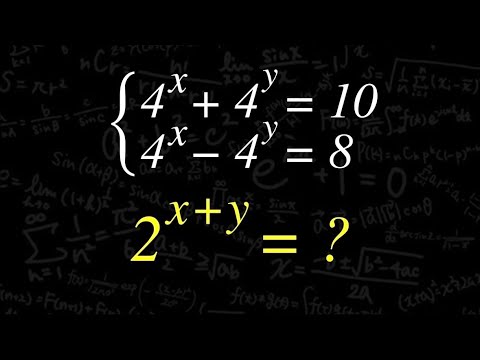
単元:
#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x + 4^y = 10 \\
4^x - 4^y = 8
\end{array}
\right.
\end{eqnarray}
$2^{x+y}= ?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x + 4^y = 10 \\
4^x - 4^y = 8
\end{array}
\right.
\end{eqnarray}
$2^{x+y}= ?$
指数連立方程式 (高校数学)
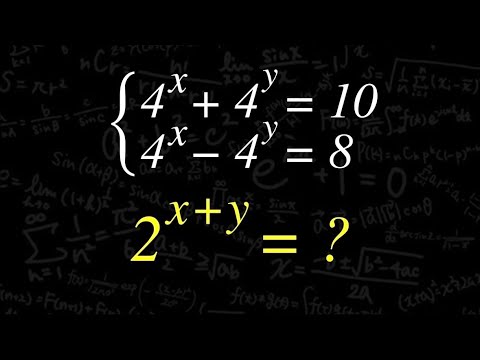
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x+4^y=10 \\
4^x-4^y=8
\end{array}
\right.
\end{eqnarray}
のとき
$2^{x+y}=?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x+4^y=10 \\
4^x-4^y=8
\end{array}
\right.
\end{eqnarray}
のとき
$2^{x+y}=?$
指数連立方程式 (高校数学)
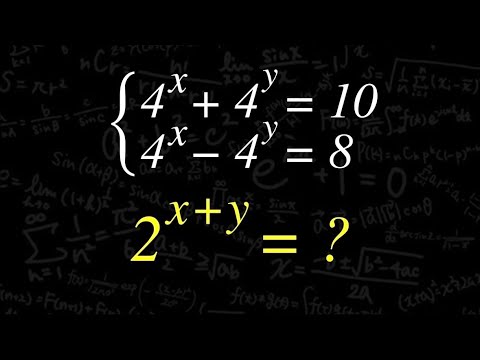
2の何とか乗