対数関数
対数関数
福田の数学〜上智大学2021年理工学部第２問(2)〜常用対数の評価
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}} (2)(\textrm{i})$不等式
$\frac{k-1}{k} \lt \log_{10}7 \lt \frac{k}{k+1}$
を満たす自然数$k$は$\boxed{\ \ ス\ \ }$である。
$(\textrm{ii})7^{35}$は$\boxed{\ \ セ\ \ }$桁の整数である。
2021上智大学理工学部過去問
この動画を見る
${\Large\boxed{2}} (2)(\textrm{i})$不等式
$\frac{k-1}{k} \lt \log_{10}7 \lt \frac{k}{k+1}$
を満たす自然数$k$は$\boxed{\ \ ス\ \ }$である。
$(\textrm{ii})7^{35}$は$\boxed{\ \ セ\ \ }$桁の整数である。
2021上智大学理工学部過去問
03東京都教員採用試験（数学：1-(1) 対数の方程式）
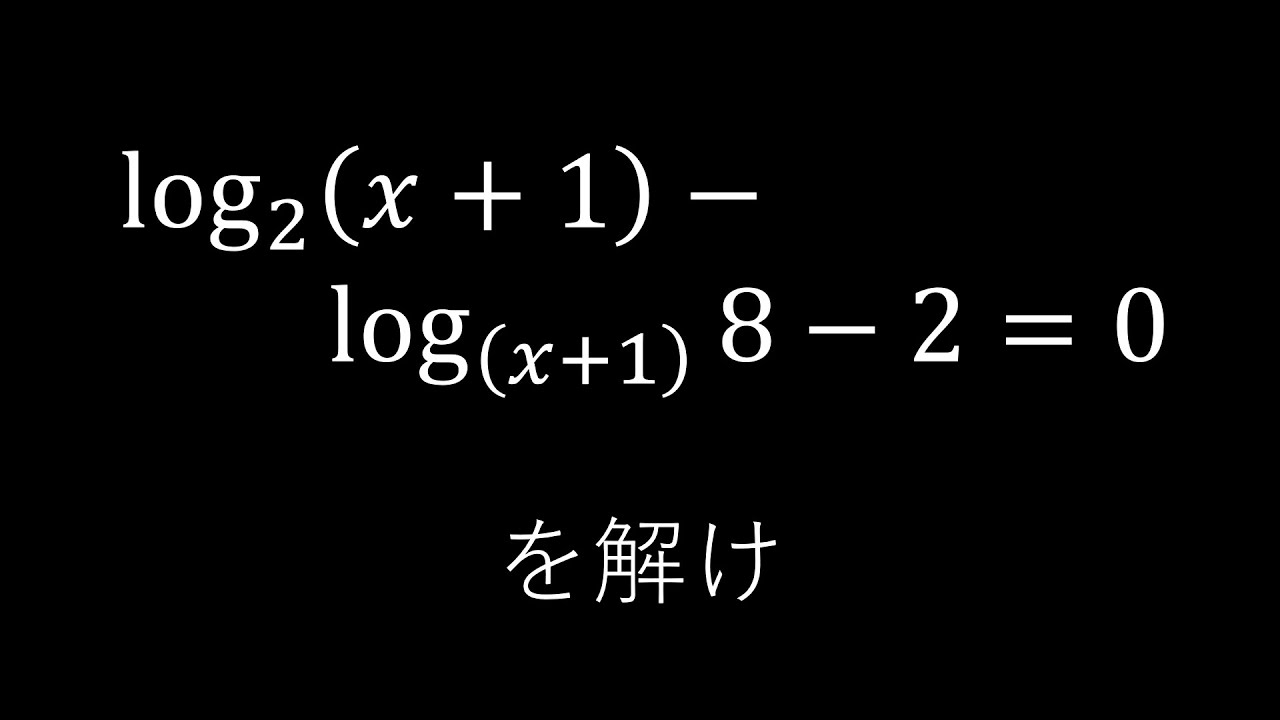
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$log_2(x+1)-log_{(x+1)}8-2=0$を解け
出典：東京都教員採用試験
この動画を見る
$log_2(x+1)-log_{(x+1)}8-2=0$を解け
出典：東京都教員採用試験
見掛け倒しの方程式 ちょっと気をつけてね
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$(\sqrt2)^{\log_2(x^2+x-6)^2}=-2x+4$
この動画を見る
これを解け.
$(\sqrt2)^{\log_2(x^2+x-6)^2}=-2x+4$
福田の数学〜中央大学2021年経済学部第１問(2)〜常用対数と桁数
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$(1)$12^{25}$は何桁の整数か.
ただし,$\log_{10}2=0.3010,\log_{10}3=0.4771$とする.
2021中央大経済学部過去問
この動画を見る
$\boxed{1}$(1)$12^{25}$は何桁の整数か.
ただし,$\log_{10}2=0.3010,\log_{10}3=0.4771$とする.
2021中央大経済学部過去問
大分大 ざ・見掛け倒しの問題
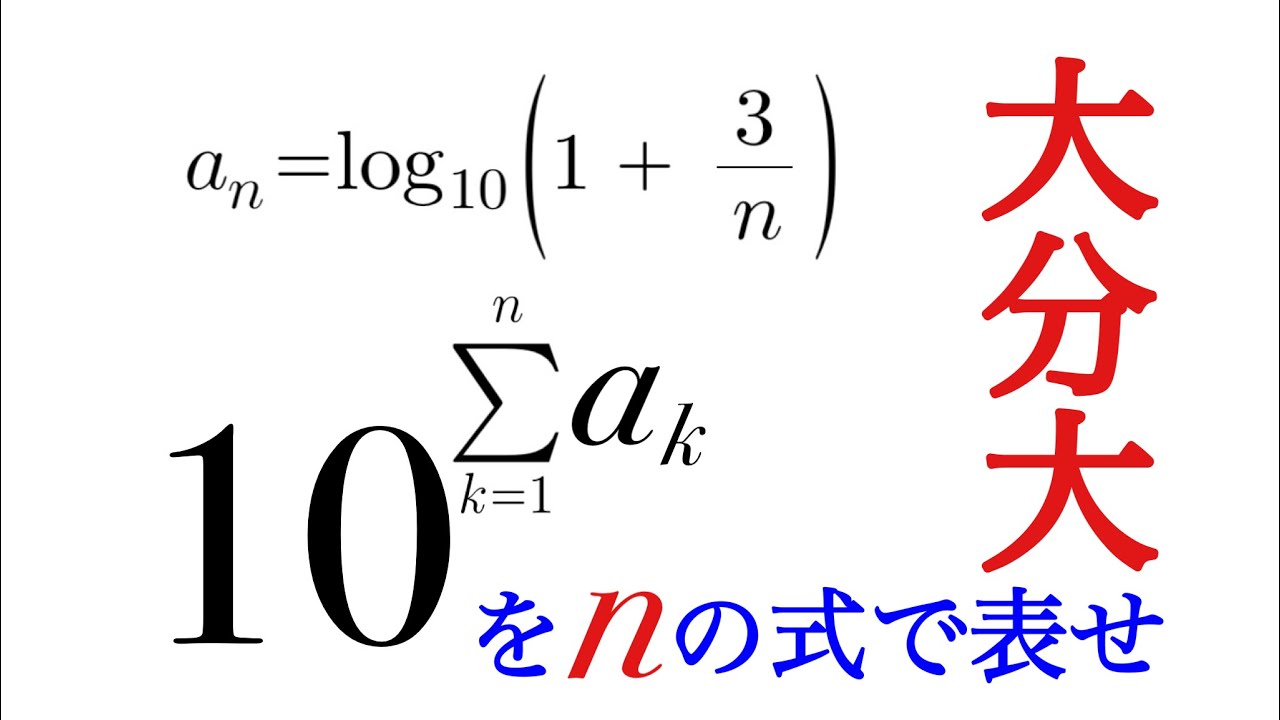
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_n=\log_{10}\left(1+\dfrac{3}{n}\right)$
$10^{\displaystyle \sum_{k=1}^n a_k}$を$n$の式で表せ.
2021大分大過去問
この動画を見る
$a_n=\log_{10}\left(1+\dfrac{3}{n}\right)$
$10^{\displaystyle \sum_{k=1}^n a_k}$を$n$の式で表せ.
2021大分大過去問
練習問題46 岡山大学 対数の性質を利用した不等式の証明 数検準１級 教員採用試験
単元：
#数Ⅱ#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#指数関数と対数関数#対数関数#微分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#岡山大学#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
実数$a,b,$は
$0 \lt a \lt b$をみたしているとき
$(b+1)^a \lt (a+1)^b$が成り立つことを表せ。
出典：岡山大学
この動画を見る
実数$a,b,$は
$0 \lt a \lt b$をみたしているとき
$(b+1)^a \lt (a+1)^b$が成り立つことを表せ。
出典：岡山大学
07高知県教員採用試験（数学：2番 対数，解の個数）
単元：
#数Ⅱ#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$a$:定数である.
$\log_3 (x-1)^2+\log_3 (x+2)=a$において
異なる2つの正の解と1つの負の解をもつように
定数$a$の値の範囲を求めよ.
この動画を見る
$\boxed{2}$
$a$:定数である.
$\log_3 (x-1)^2+\log_3 (x+2)=a$において
異なる2つの正の解と1つの負の解をもつように
定数$a$の値の範囲を求めよ.
03兵庫県教員採用試験（数学：5-(2) 共有点の個数）
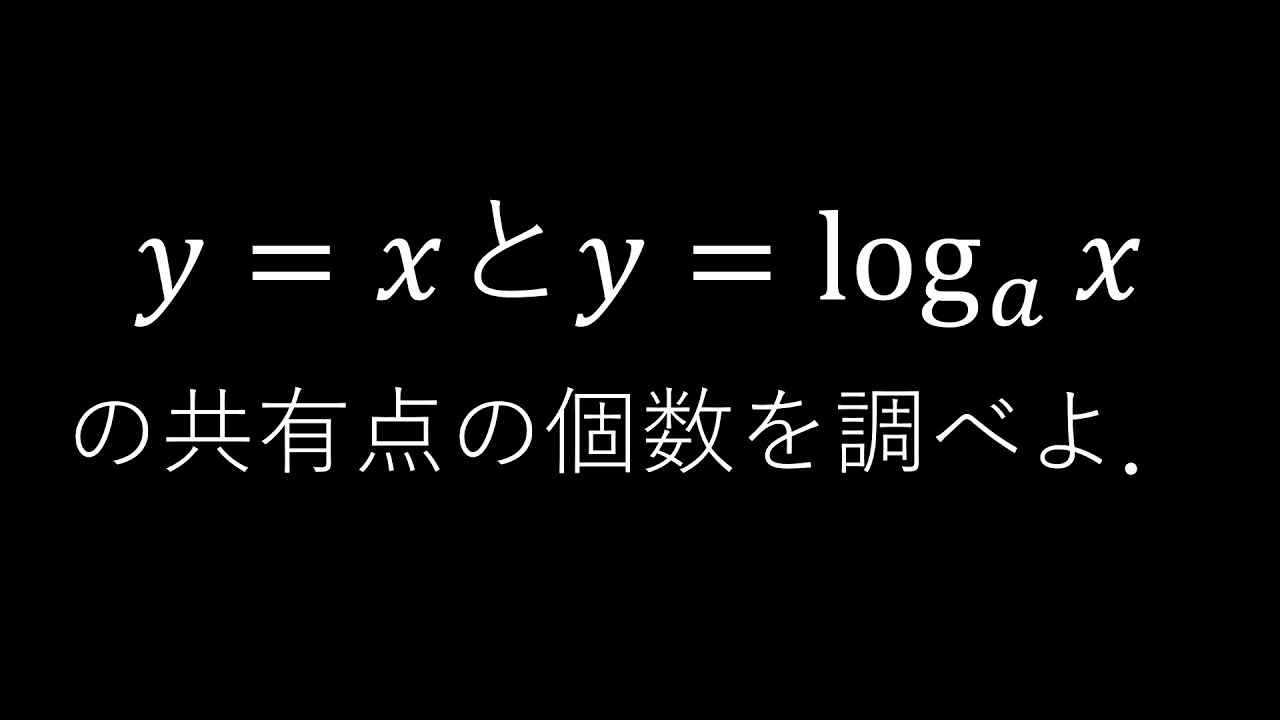
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}(2)$
直線$y=x$と曲線$y=\log_a x$との
共有点の個数を調べよ.
この動画を見る
$\boxed{5}(2)$
直線$y=x$と曲線$y=\log_a x$との
共有点の個数を調べよ.
結局0の0乗っていくつになるの？
単元：
#算数(中学受験)#数学(中学生)#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
0の0乗は何になるか
この動画を見る
0の0乗は何になるか
航空大学校 対数の基本
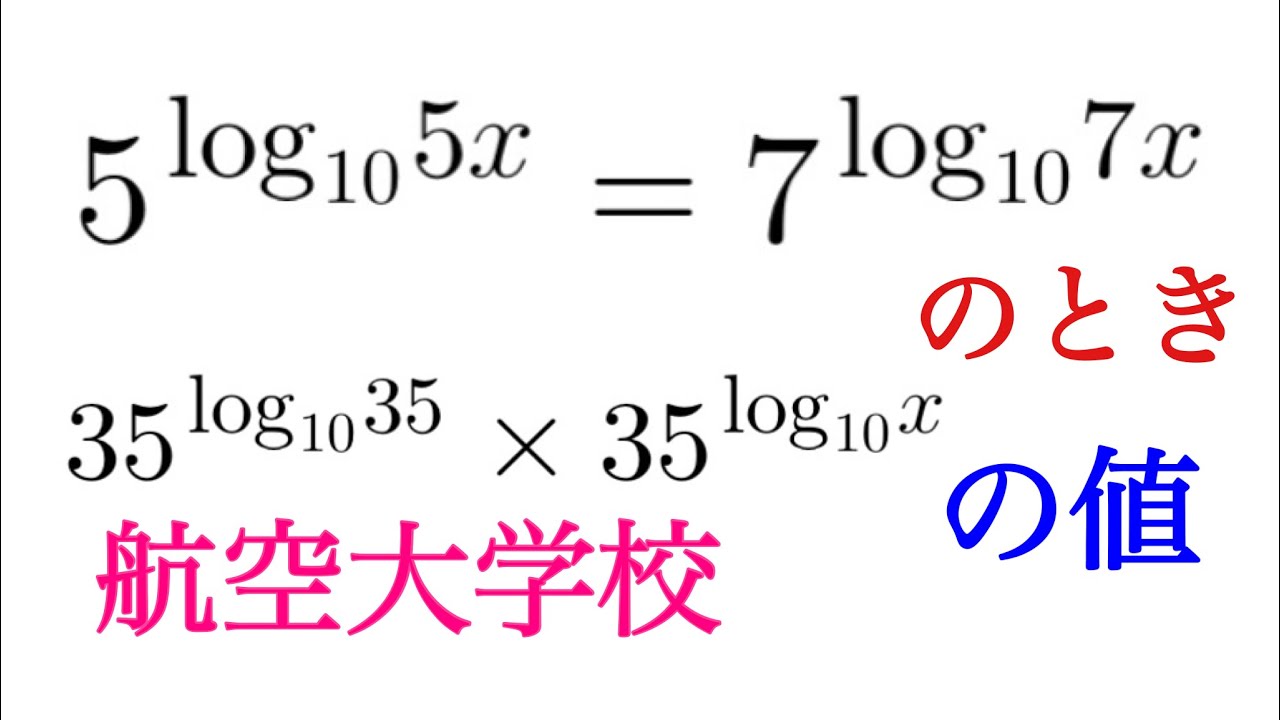
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$5^{\log_{10}5x}=7^{\log_{10}7x}$
$35^{\log_{10}35}\times 35^{\log_{10}x}$の値を求めよ.
航空大学校過去問
この動画を見る
$5^{\log_{10}5x}=7^{\log_{10}7x}$
$35^{\log_{10}35}\times 35^{\log_{10}x}$の値を求めよ.
航空大学校過去問
指数・対数・対称式
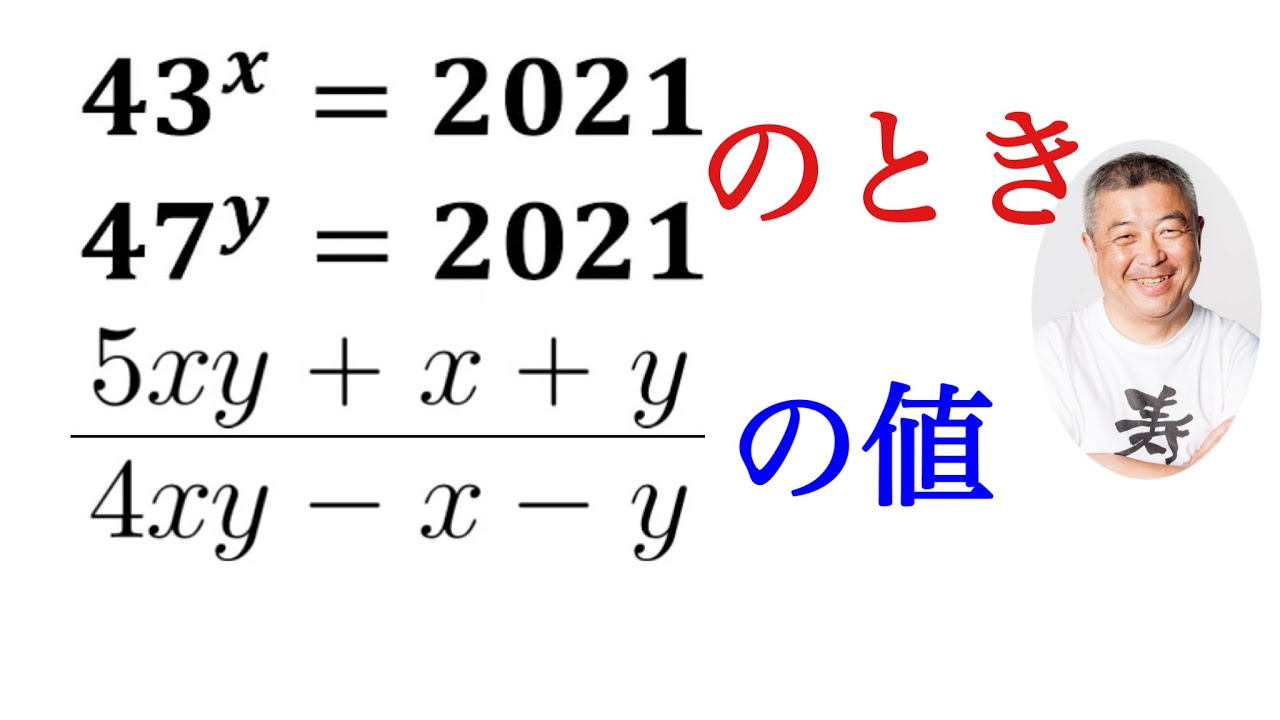
単元：
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
43^x=2021 \\
47^y=2021
\end{array}
\right.
\end{eqnarray}$
$\dfrac{5xy+x+y}{4xy-x-y}$の値を求めよ.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
43^x=2021 \\
47^y=2021
\end{array}
\right.
\end{eqnarray}$
$\dfrac{5xy+x+y}{4xy-x-y}$の値を求めよ.
高専数学 微積II #7 極値の判定
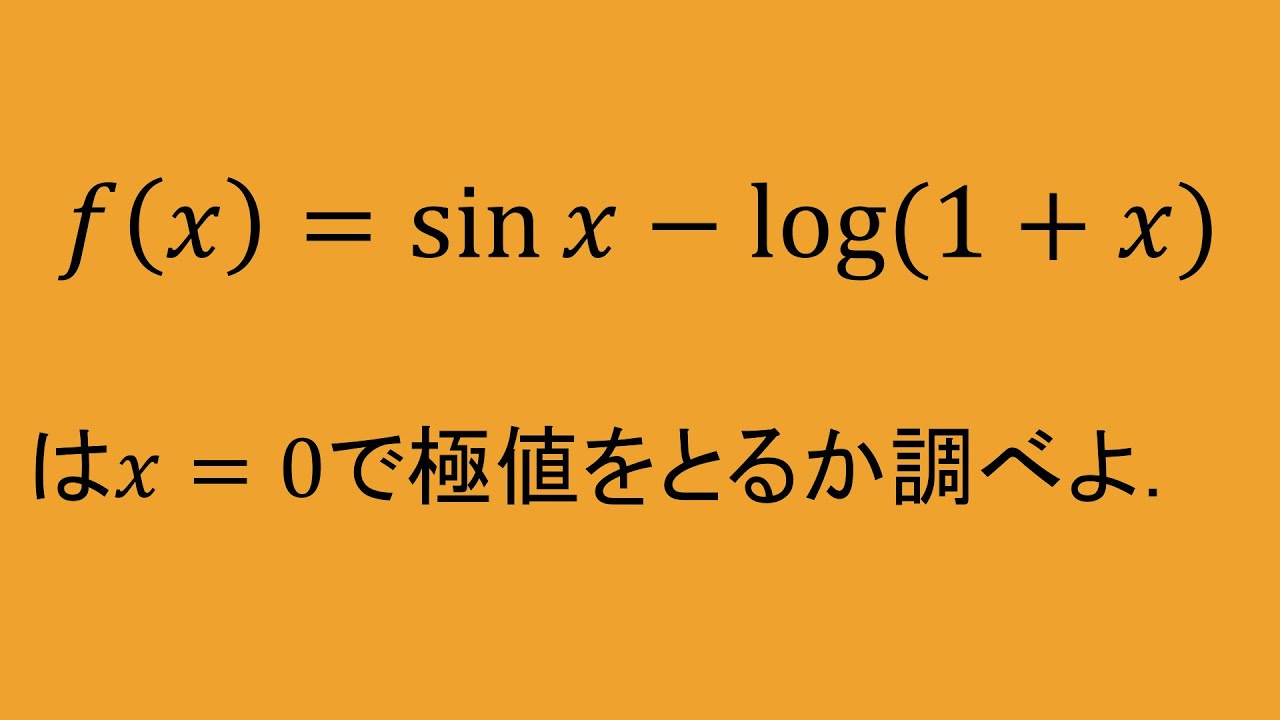
単元：
#数Ⅱ#指数関数と対数関数#微分法と積分法#対数関数#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\sin x-\log(1+x)$は$x=0$で
極値をとるか調べよ.
この動画を見る
$f(x)=\sin x-\log(1+x)$は$x=0$で
極値をとるか調べよ.
06滋賀県教員採用試験（数学：5番 対数の性質）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
$x,y$:正の整数である.
$x^2$が7桁,$xy^3$が20桁になるとき,
$x,y$は何桁であるか求めよ.
この動画を見る
$\boxed{5}$
$x,y$:正の整数である.
$x^2$が7桁,$xy^3$が20桁になるとき,
$x,y$は何桁であるか求めよ.
福田の数学〜慶應義塾大学2021年商学部第１問(1)〜対数の基本性質
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$
(1)正の実数$x,\ y$について、xとyの相加平均を5とする。また、4を底とする。
$x,\ y$の対数をそれぞれ$X,\ Y$としたとき、XとYの相加平均は1であるとする。
このとき、$x \lt y$とすると、$x=\boxed{\ \ ア\ \ }, y=\boxed{\ \ イ\ \ }$ である。
2021慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(1)正の実数$x,\ y$について、xとyの相加平均を5とする。また、4を底とする。
$x,\ y$の対数をそれぞれ$X,\ Y$としたとき、XとYの相加平均は1であるとする。
このとき、$x \lt y$とすると、$x=\boxed{\ \ ア\ \ }, y=\boxed{\ \ イ\ \ }$ である。
2021慶應義塾大学商学部過去問
名古屋大学２００２どっちがでかいか？
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
どちらが大きいか?
①$\ell_n\left(1+\dfrac{1}{x}\right)$ vs $\dfrac{1}{x+1}$
②$\left(1+\dfrac{2002}{2001}\right)^{\frac{2001}{2002}}$ vs $\left(1+\dfrac{2001}{2002}\right)^{\frac{2002}{2001}}$
この動画を見る
どちらが大きいか?
①$\ell_n\left(1+\dfrac{1}{x}\right)$ vs $\dfrac{1}{x+1}$
②$\left(1+\dfrac{2002}{2001}\right)^{\frac{2001}{2002}}$ vs $\left(1+\dfrac{2001}{2002}\right)^{\frac{2002}{2001}}$
20三重県教員採用試験（数学：1-(3) 対数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(3)$
$x \geq 3,y \geq \dfrac{1}{3},xy^2=243$
のとき
$\left(\log_3 x\right)\left(\log_3 y\right)$
の最大値,最小値を求めよ.
この動画を見る
$\boxed{1}-(3)$
$x \geq 3,y \geq \dfrac{1}{3},xy^2=243$
のとき
$\left(\log_3 x\right)\left(\log_3 y\right)$
の最大値,最小値を求めよ.
対数の基本
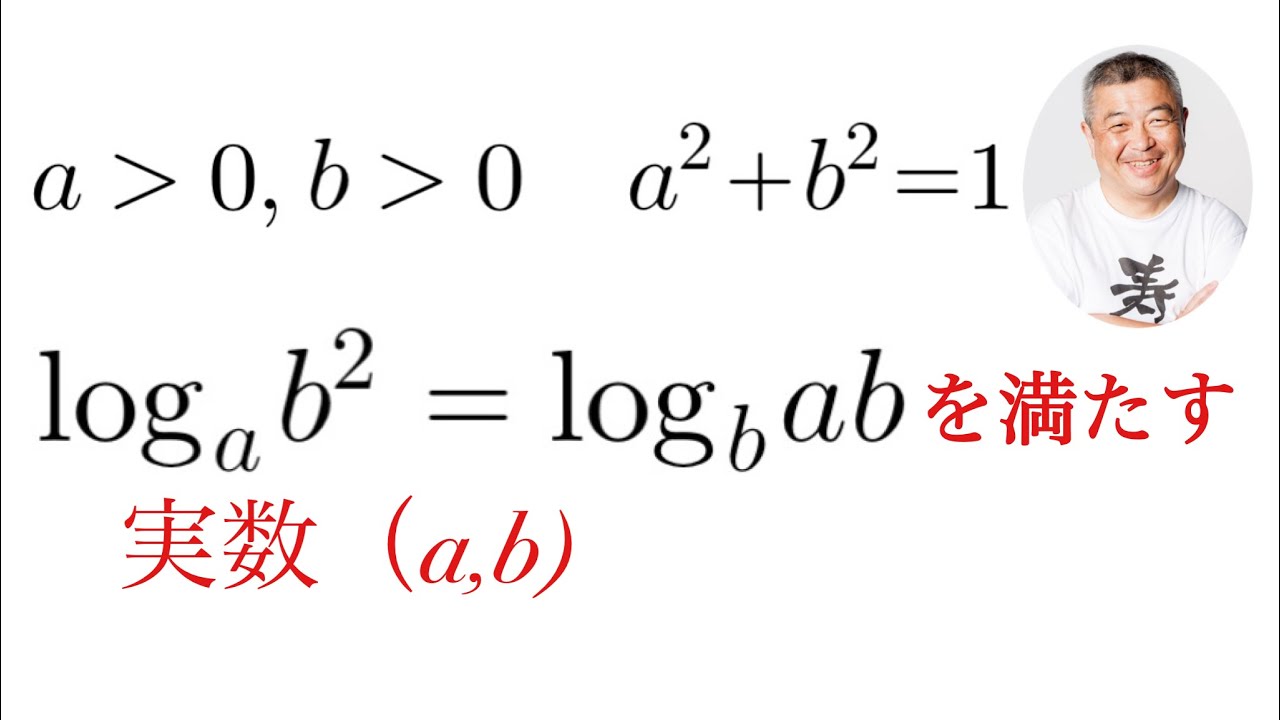
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a\gt 0,b\gt 0$
$a^2+b^2=1$
$\log_a b^2=\log_b ab$
実数$(a,b)$を求めよ.
この動画を見る
$a\gt 0,b\gt 0$
$a^2+b^2=1$
$\log_a b^2=\log_b ab$
実数$(a,b)$を求めよ.
対数の基本性質
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを簡単にせよ.$a,b,c$を正とし,$a,b,c \neq 1$である.
$\dfrac{1}{1+\log_a bc}+\dfrac{1}{1+\log_b ca}+\dfrac{1}{1+\log_c ab}$
この動画を見る
これを簡単にせよ.$a,b,c$を正とし,$a,b,c \neq 1$である.
$\dfrac{1}{1+\log_a bc}+\dfrac{1}{1+\log_b ca}+\dfrac{1}{1+\log_c ab}$
福田の数学〜早稲田大学2021年人間科学部第２問(1)〜指数対数不等式の表す領域の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#軌跡と領域#指数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$
(1)次の連立不等式の表す領域の面積は$\dfrac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}$ である。
$\left\{\begin{array}{1}
\displaystyle\log_4y+\log_{\frac{1}{4}}(x-2)+\log_4\frac{1}{8-x} \geqq -1\\
2^{y+x^2+11} \leqq 1024^{x-1}\\
\end{array}\right.$
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{2}}$
(1)次の連立不等式の表す領域の面積は$\dfrac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}$ である。
$\left\{\begin{array}{1}
\displaystyle\log_4y+\log_{\frac{1}{4}}(x-2)+\log_4\frac{1}{8-x} \geqq -1\\
2^{y+x^2+11} \leqq 1024^{x-1}\\
\end{array}\right.$
2021早稲田大学人間科学部過去問
16和歌山県教員採用試験（数学：6番 対数の不等式）
単元：
#数Ⅰ#数Ⅱ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
この動画を見る
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
06岡山教員採用試験（数学：対数の計算）
数学「大学入試良問集」【9−3 対数関数と領域図示】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$log_2\ y+2log_y\ x \leqq 3$を満たす点$(x,y)$の存在する領域を図示せよ。
この動画を見る
$log_2\ y+2log_y\ x \leqq 3$を満たす点$(x,y)$の存在する領域を図示せよ。
15和歌山県教員採用試験（数学：1 -(7) 対数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(7)$
$\log_{10}2=a,\log_{10}3=b$とする.
$\log_{3}32$を$a,b$で表せ.
この動画を見る
$\boxed{1}-(7)$
$\log_{10}2=a,\log_{10}3=b$とする.
$\log_{3}32$を$a,b$で表せ.
数学「大学入試良問集」【9−2 常用対数と最高位の数】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$6^n$が$39$桁の自然数になるときの自然数$n$を求めよ。
その場合の$n$に対する$6^n$の最高位の数字を求めよ。
ただし、$log_{10}2=0.3010,log_{10}3=0.4771$とする。
この動画を見る
$6^n$が$39$桁の自然数になるときの自然数$n$を求めよ。
その場合の$n$に対する$6^n$の最高位の数字を求めよ。
ただし、$log_{10}2=0.3010,log_{10}3=0.4771$とする。
07愛知県教員採用試験（数学：6番 対数関数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
$f(x)=\log_2 (x+2)+\log_4 (4-x)$の
最大値を求めよ.
この動画を見る
$\boxed{6}$
$f(x)=\log_2 (x+2)+\log_4 (4-x)$の
最大値を求めよ.
３通りの解法 首都大
単元：
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\log_{10}x+\log_{10}y=\log_{10}(y+2x^2+1)$
整数＄(x,y)$を全て求めよ.
2008首都大過去問
この動画を見る
$\log_{10}x+\log_{10}y=\log_{10}(y+2x^2+1)$
整数＄(x,y)$を全て求めよ.
2008首都大過去問
13愛知県教員採用試験（数学：6番 対数の性質）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
$\log_{10} 2=0.3010$
$\log_{10} 3=0.4771$
(1)$3^{25}$は何桁
(2)$3^{25}$の最高位の数
(3)$3^{25}$の1の位の数
この動画を見る
$\boxed{6}$
$\log_{10} 2=0.3010$
$\log_{10} 3=0.4771$
(1)$3^{25}$は何桁
(2)$3^{25}$の最高位の数
(3)$3^{25}$の1の位の数
03兵庫県教員採用試験（数学：5番 交点の個数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
$0\lt a\neq 1$とする.
$y=x$と$y-\log_a x$の
交点の個数を調べよ.
この動画を見る
$\boxed{5}$
$0\lt a\neq 1$とする.
$y=x$と$y-\log_a x$の
交点の個数を調べよ.
09愛知県教員採用試験（数学：3番 指数・対数）
単元：
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$25^{\log_5 3^x}-4\sqrt3･3^x=-9$を解け.
この動画を見る
$\boxed{3}$
$25^{\log_5 3^x}-4\sqrt3･3^x=-9$を解け.
対数の大小比較
