 不定積分・定積分
不定積分・定積分
 不定積分・定積分
不定積分・定積分
#高専数学_12#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{3x^2+1} dx$
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{3x^2+1} dx$
#茨城大学2024#定積分_2#元高校教員
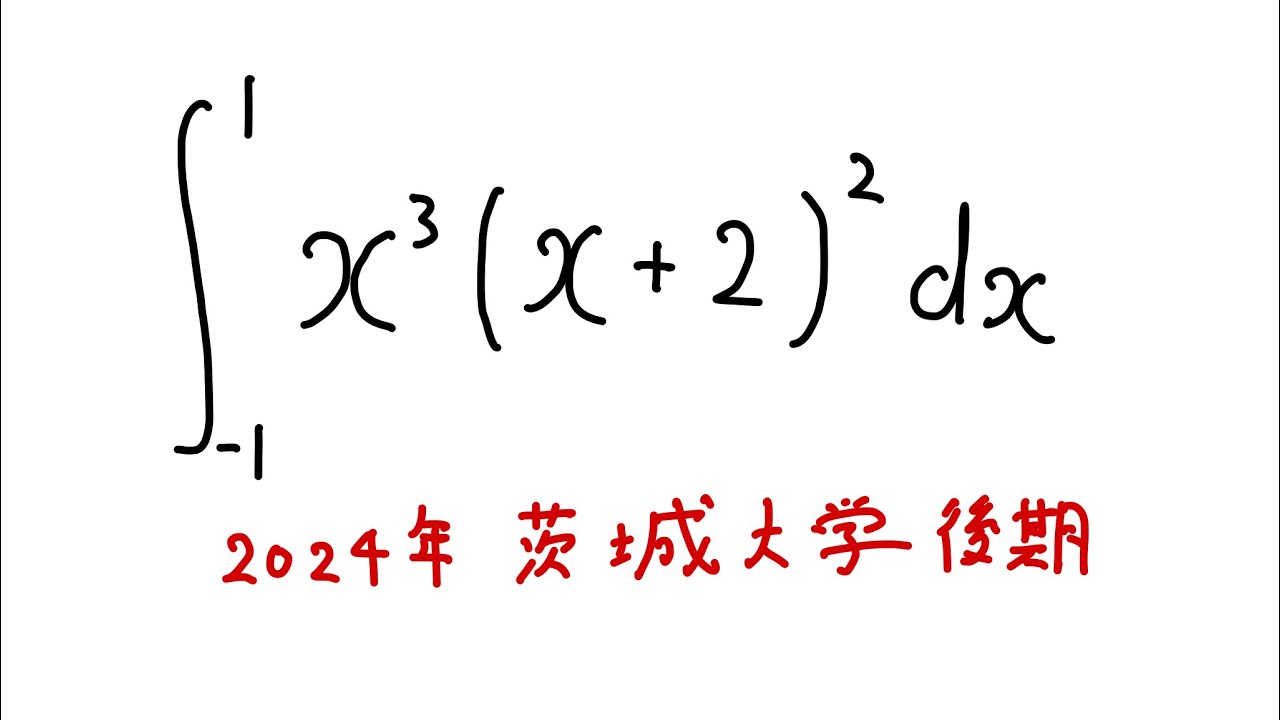
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
大学入試問題#616「これは理系が解くと逆にはまるかも」 名古屋大学(1963)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt y$とする
$x+y=6,\ xy=4$のとき
$\displaystyle \frac{\sqrt{ x }-\sqrt{ y }}{\sqrt{ x }+\sqrt{ y }}$の値を求めよ。
出典:1963年名古屋大学 入試問題
この動画を見る
$x \gt y$とする
$x+y=6,\ xy=4$のとき
$\displaystyle \frac{\sqrt{ x }-\sqrt{ y }}{\sqrt{ x }+\sqrt{ y }}$の値を求めよ。
出典:1963年名古屋大学 入試問題
大学入試問題#904「解き方いろいろ」 #お茶の水女子大学(2013) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$で
$f(x)+\displaystyle \int_{1}^{x} \displaystyle \frac{f(t)}{t}dt=3x^2-2x$を満たす多項式$f(x)$を求めよ。
出典:2013年お茶の水女子大学
この動画を見る
$x \gt 0$で
$f(x)+\displaystyle \int_{1}^{x} \displaystyle \frac{f(t)}{t}dt=3x^2-2x$を満たす多項式$f(x)$を求めよ。
出典:2013年お茶の水女子大学
#高専数学_11#定積分#元高専教員
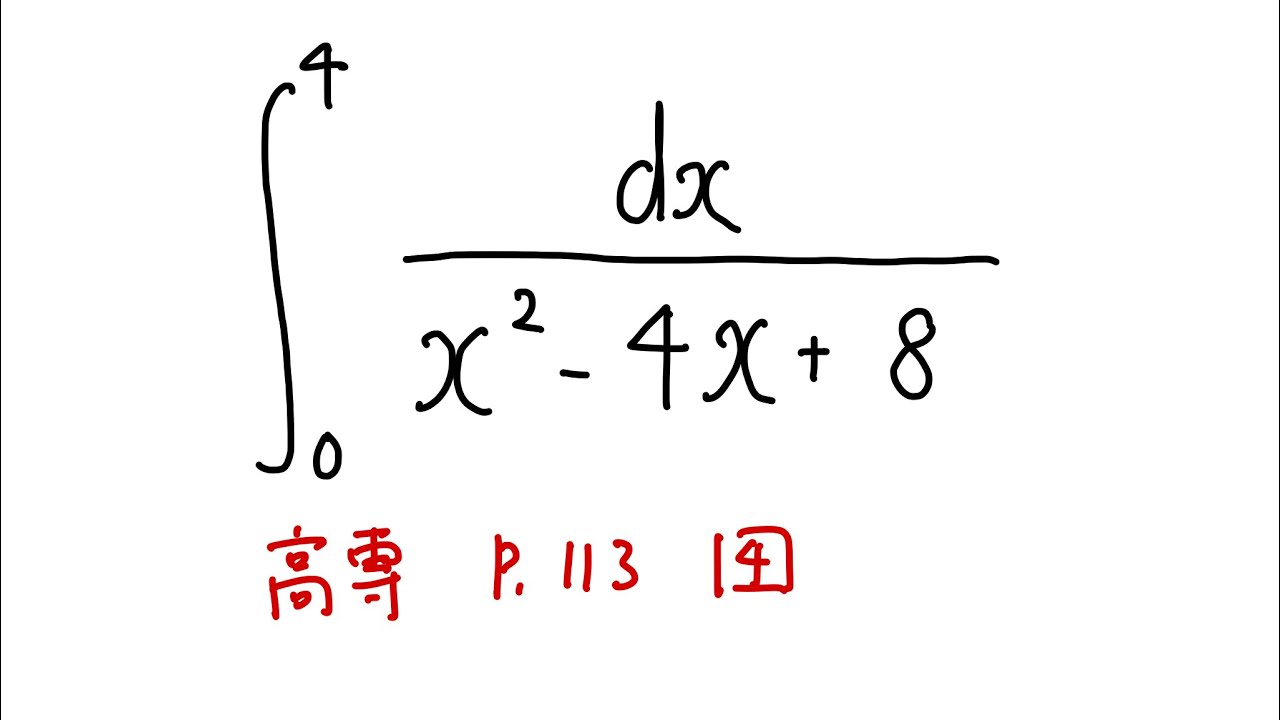
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{dx}{x^2-4x+8}$
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{dx}{x^2-4x+8}$
#茨城大学2024_1#定積分
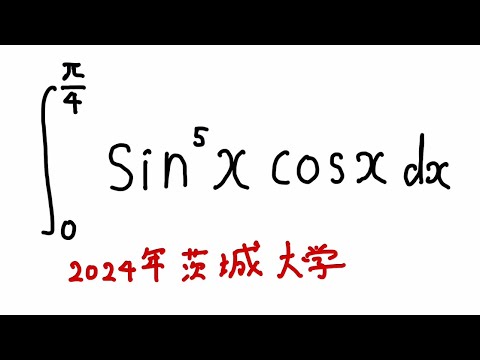
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
#高専数学_10#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{(x-2)^2} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{(x-2)^2} dx$
#高専数学_9#不定積分#元高専教員
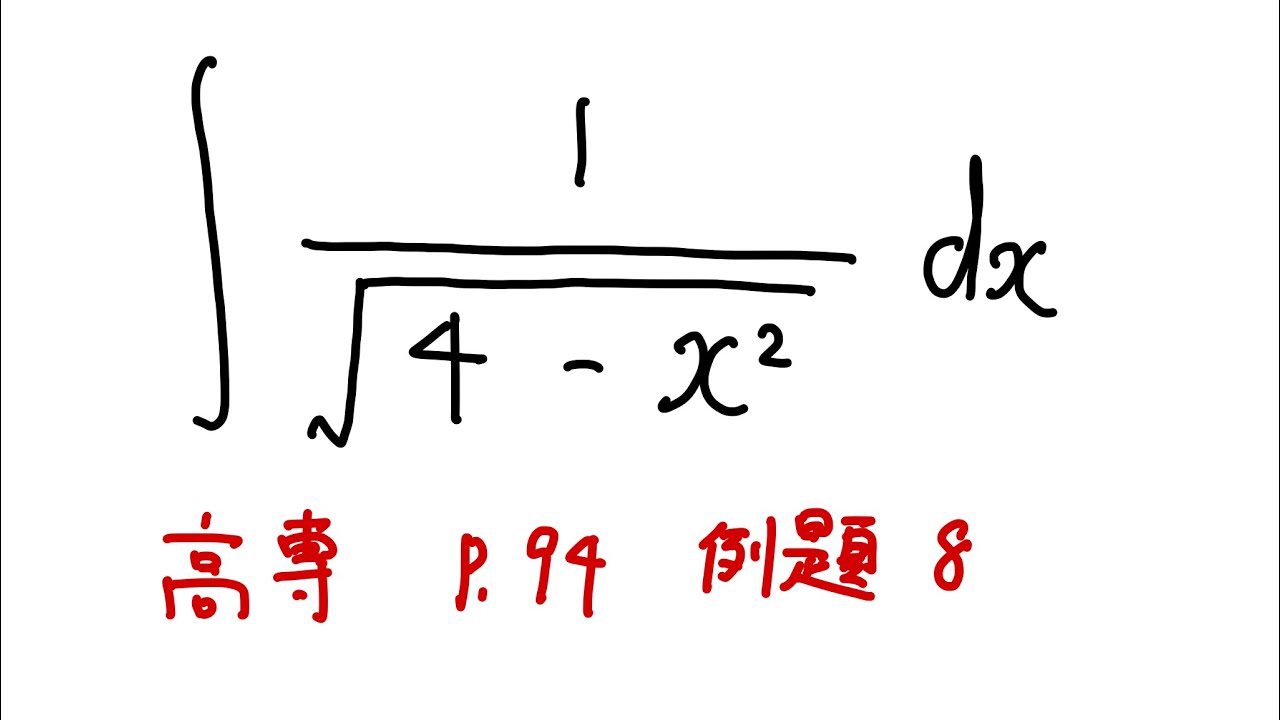
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の不定積分を解け。
$\displaystyle \int \displaystyle \frac{1}{\sqrt{ 4-x^2 }} dx$
この動画を見る
下記の不定積分を解け。
$\displaystyle \int \displaystyle \frac{1}{\sqrt{ 4-x^2 }} dx$
#千葉大学2016#定積分#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
大学入試問題#901「基本だけど初手大事」 #電気通信大学(2024)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \sqrt{ 2-\sqrt{ x} }$ $dx$
出典:2024年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{4} \sqrt{ 2-\sqrt{ x} }$ $dx$
出典:2024年電気通信大学
福田の数学〜中央大学2024経済学部第1問(6)〜定積分で表された関数

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x)$ は
$\displaystyle f(x)=x^2 \int^{2}_{0} f'(t) dt +Ax, \quad f(1)=1$
を満たしている。ただし、$A$ は定数である。このとき、$f(x)$ が最大になる $x$ を求めよ。
この動画を見る
関数 $f(x)$ は
$\displaystyle f(x)=x^2 \int^{2}_{0} f'(t) dt +Ax, \quad f(1)=1$
を満たしている。ただし、$A$ は定数である。このとき、$f(x)$ が最大になる $x$ を求めよ。
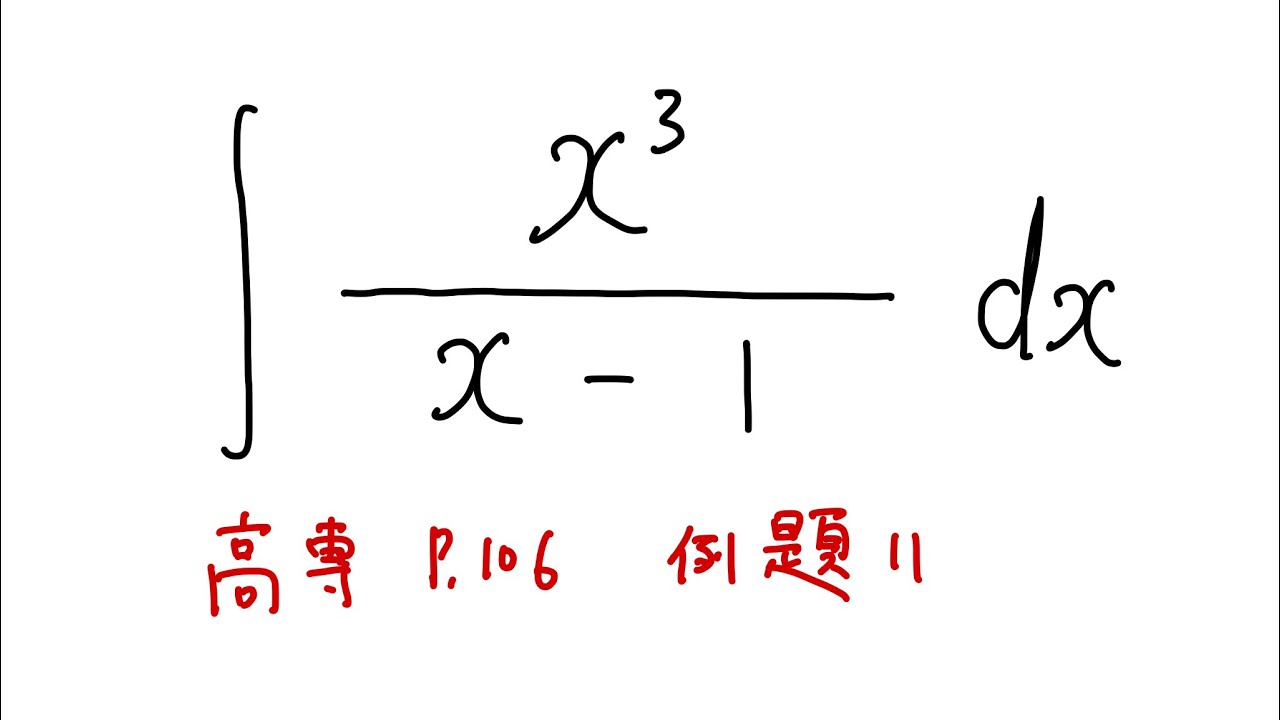
#高専_8#不定積分#元高専教員
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{x-1}$ $dx$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{x-1}$ $dx$
#千葉大学2021#不定積分#元高専教員
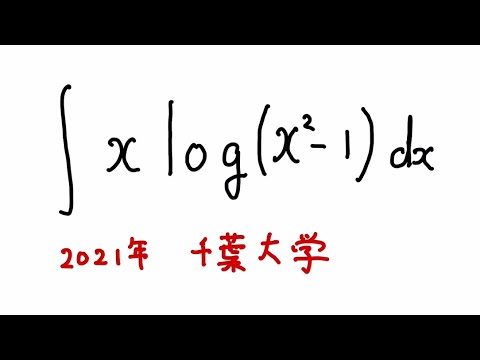
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
積分区間は0→π/4です。大学入試問題#900「減点ポイント多い問題」 #横浜国立大学後期(2023)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$を正の整数とする。
関数$F(x)=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{2e^x\cos t\sin t}{(\cos^2t+x^n\sin^2t)^2} dt$
について、次の問いに答えよ。
ただし、$x \gt 0$とする。
1.$F(x)$を求めよ。
2.$F(x)$が極値をもつ最小の$n$の値を求めよ。
出典:2023年横浜国立大学後期
この動画を見る
$n$を正の整数とする。
関数$F(x)=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{2e^x\cos t\sin t}{(\cos^2t+x^n\sin^2t)^2} dt$
について、次の問いに答えよ。
ただし、$x \gt 0$とする。
1.$F(x)$を求めよ。
2.$F(x)$が極値をもつ最小の$n$の値を求めよ。
出典:2023年横浜国立大学後期
#高専_7#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\sqrt{ 2 }} \displaystyle \frac{1+2x}{\sqrt{ 4-x^2 }} dx$
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\sqrt{ 2 }} \displaystyle \frac{1+2x}{\sqrt{ 4-x^2 }} dx$
#千葉大学2018#不定積分#数学者
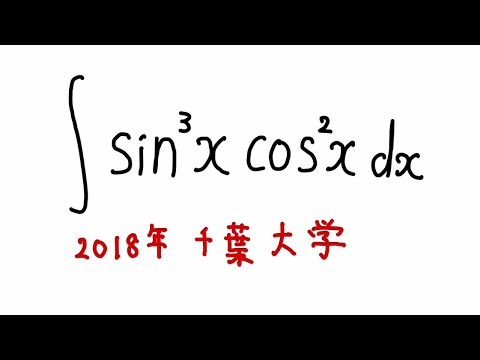
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
#高専_6#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int (3x+1)\cos2x$ $dx$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int (3x+1)\cos2x$ $dx$
大学入試問題#898「教科書例題」 #千葉大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす$x \gt 0$で定義された関数$f(x)$と定数$a$の値を求めよ。
ただし、$a \gt 0$とする。
$\displaystyle \int_{a}^{x} f(t) dt=x+\displaystyle \frac{1}{2}log$ $x-1$
出典:2024年千葉大学
この動画を見る
次の等式を満たす$x \gt 0$で定義された関数$f(x)$と定数$a$の値を求めよ。
ただし、$a \gt 0$とする。
$\displaystyle \int_{a}^{x} f(t) dt=x+\displaystyle \frac{1}{2}log$ $x-1$
出典:2024年千葉大学
#高専数学_5#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の不定積分を解け。
$\displaystyle \int x log (x+1)$ $dx$
この動画を見る
下記の不定積分を解け。
$\displaystyle \int x log (x+1)$ $dx$
#千葉大学2020#不定積分#ますただ
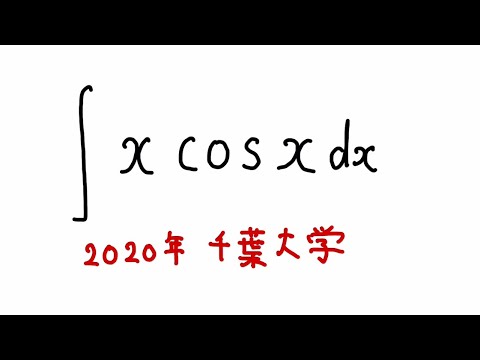
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
この動画を見る
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
#高専_4#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{(log t)^2}{t} dt$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{(log t)^2}{t} dt$
#高専_3#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
この動画を見る
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
#高専_2#定積分

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
この動画を見る
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
微分法と積分法 数Ⅱ定積分:1/6公式の使い方【烈's study!がていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \int_{α}^{ β } (x-α)(x-β)dx=-\dfrac{1}{6}(β-α)^3$を用いて、次の定積分を求めよ。
(1)$\displaystyle \int_{-1}^{ 2 } (x^2-x-2)dx$
(2)$\displaystyle \int_{1-\sqrt{2} }^{1+\sqrt{2}} (x^2-2x-1)dx$
(3)$\displaystyle \int_{3}^{ 4 } (14x-24-2x^2)dx$
この動画を見る
$\displaystyle \int_{α}^{ β } (x-α)(x-β)dx=-\dfrac{1}{6}(β-α)^3$を用いて、次の定積分を求めよ。
(1)$\displaystyle \int_{-1}^{ 2 } (x^2-x-2)dx$
(2)$\displaystyle \int_{1-\sqrt{2} }^{1+\sqrt{2}} (x^2-2x-1)dx$
(3)$\displaystyle \int_{3}^{ 4 } (14x-24-2x^2)dx$
#高専#不定積分-1

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 4-x^2 }} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 4-x^2 }} dx$
#千葉大学2024#定積分
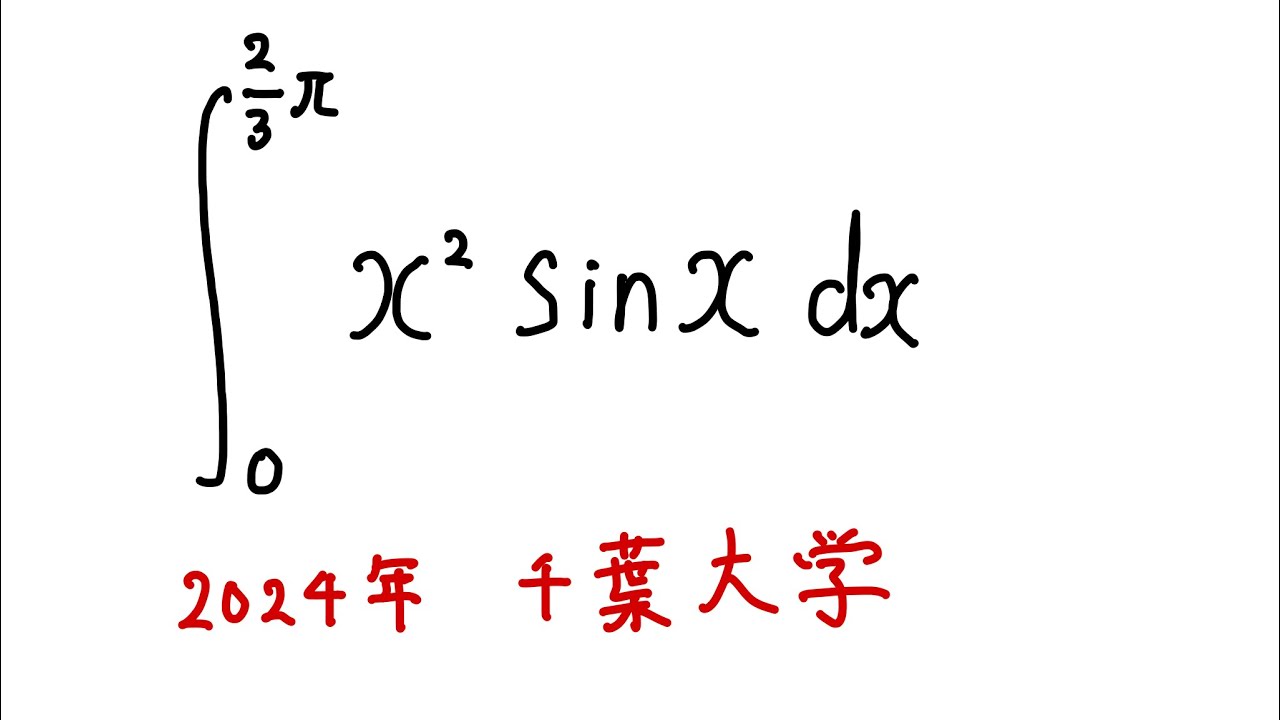
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
#千葉大学2023#定積分#ますただ
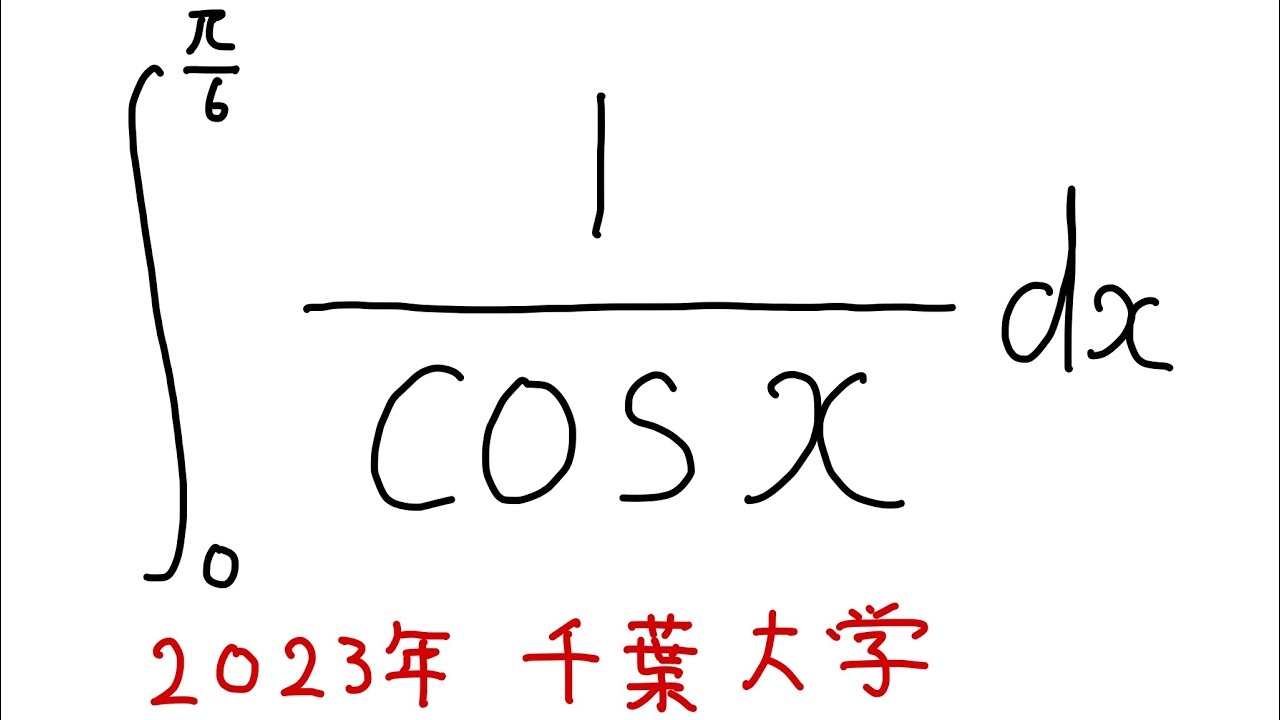
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
#千葉大学2023#定積分
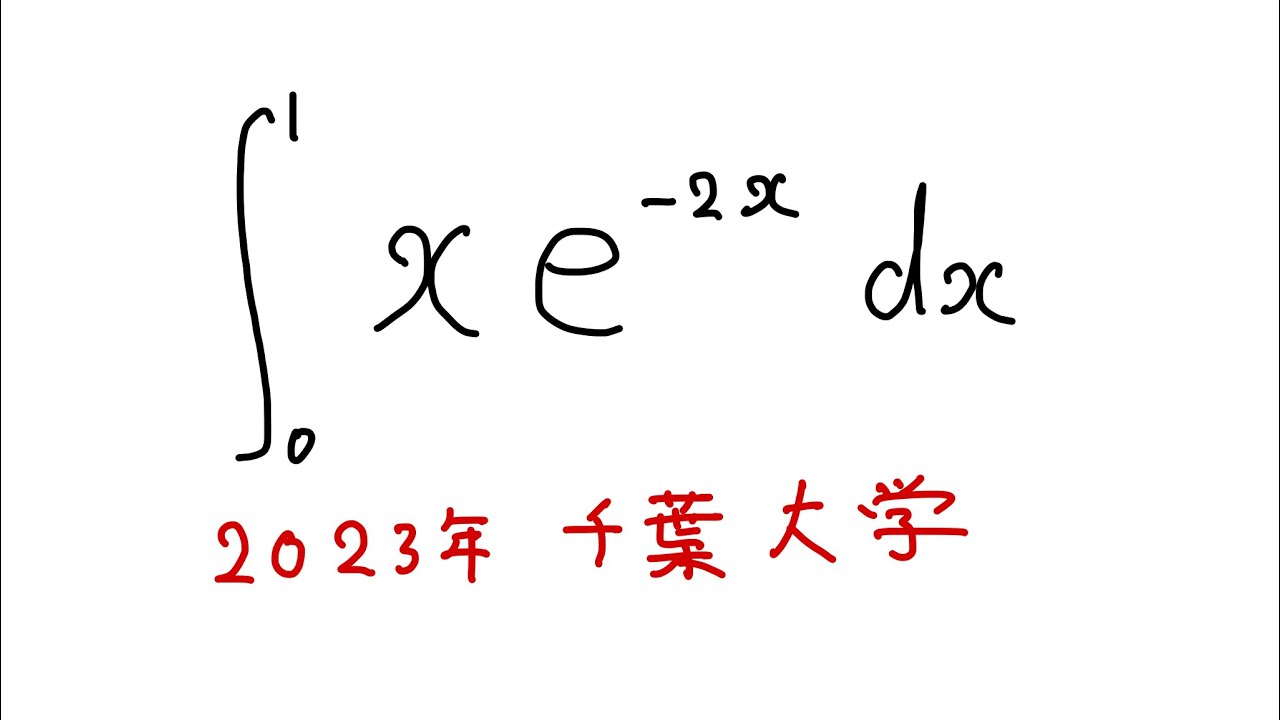
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
#広島市立大学#不定積分#ますただ
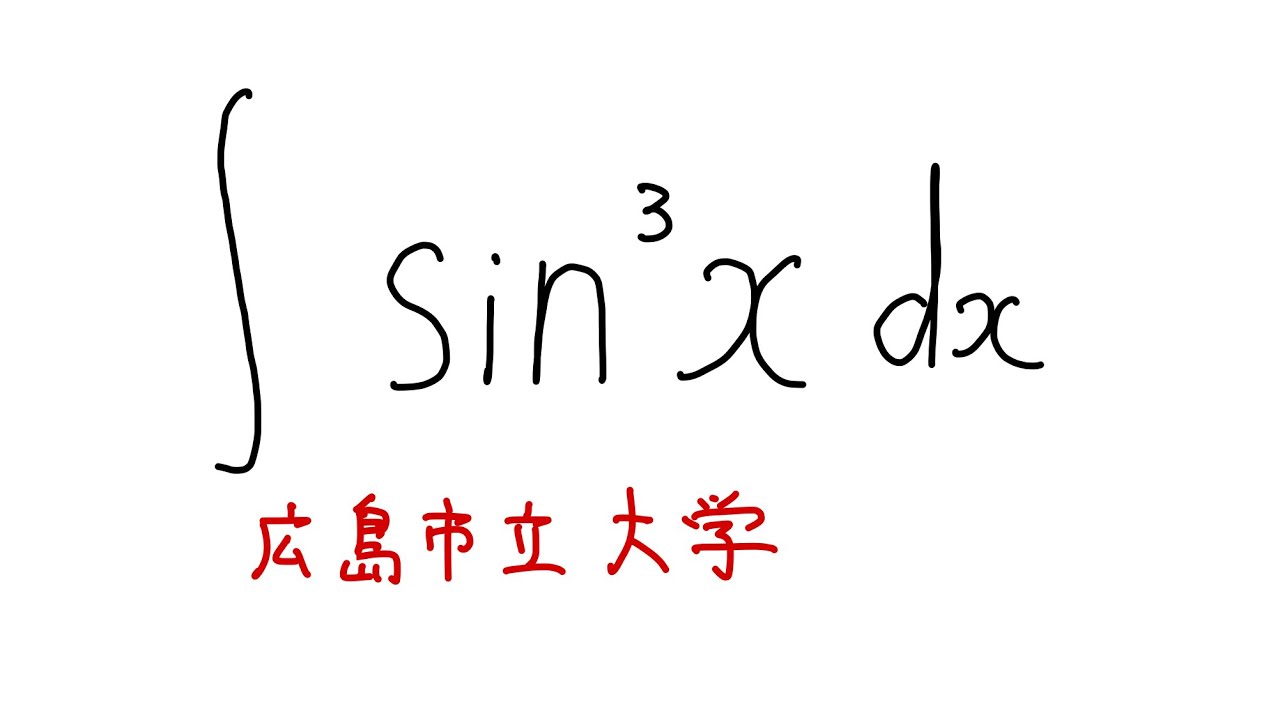
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
この動画を見る
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
#電気通信大学2015#区分求積法#ますただ
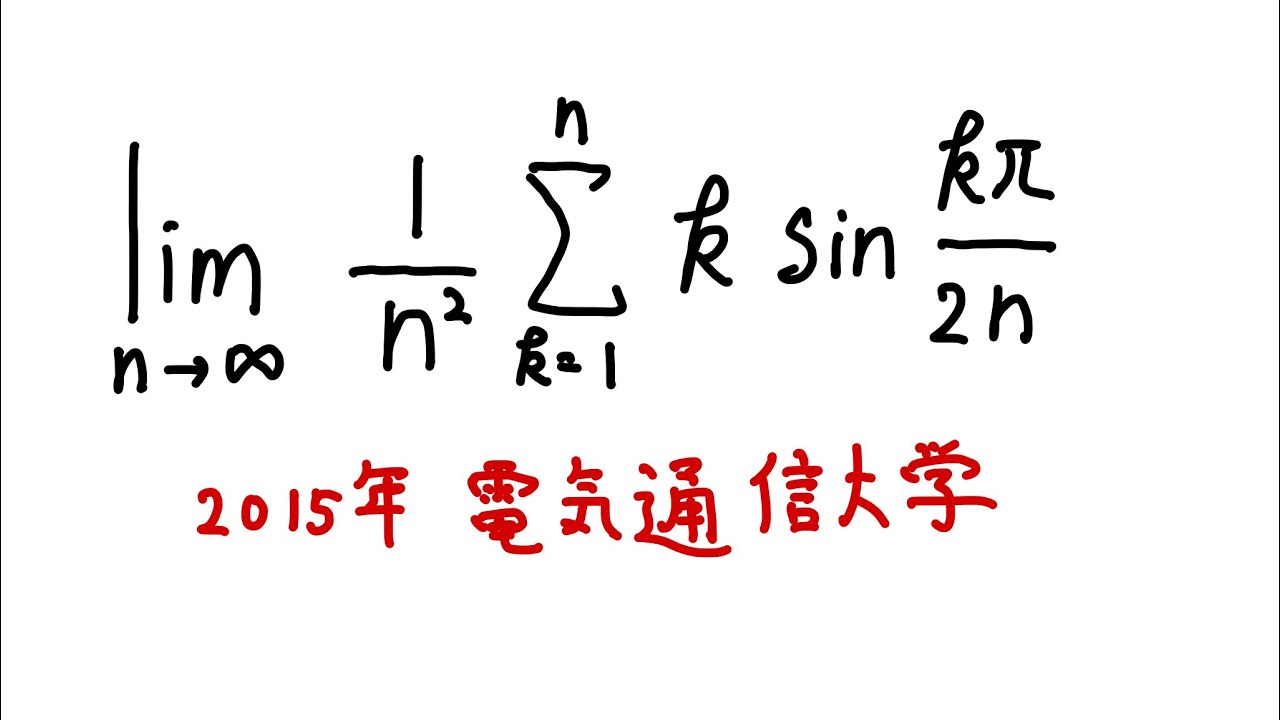
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2}\displaystyle \sum_{k=1}^n k \sin\displaystyle \frac{k\pi}{2n}$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2}\displaystyle \sum_{k=1}^n k \sin\displaystyle \frac{k\pi}{2n}$
出典:2015年電気通信大学
