 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
福田の数学〜神戸大学2024年理系第2問〜放物線と2接線た作る三角形の重心の軌跡

単元:
#数Ⅱ#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $a$, $b$, $c$は実数で、$a$≠0とする。放物線$C$と直線$l_1$, $l_2$をそれぞれ
$C$:$y$=$ax^2$+$bx$+$c$
$l_1$:$y$=$-3x$+3
$l_2$:$y$=$x$+3
で定める。$l_1$, $l_2$がともに$C$と接するとき、以下の問いに答えよ。
(1)$b$を求めよ。$c$を$a$を用いて表せ。
(2)$C$が$x$軸と異なる2点で交わるとき、$\displaystyle\frac{1}{a}$のとりうる値の範囲を求めよ。
(3)$C$と$l_1$の接点をP、$C$と$l_2$の接点をQ、放物線$C$の頂点をRとする。$a$が(2)の条件を満たしながら動くとき、$\triangle PQR$の重心Gの軌跡を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$, $b$, $c$は実数で、$a$≠0とする。放物線$C$と直線$l_1$, $l_2$をそれぞれ
$C$:$y$=$ax^2$+$bx$+$c$
$l_1$:$y$=$-3x$+3
$l_2$:$y$=$x$+3
で定める。$l_1$, $l_2$がともに$C$と接するとき、以下の問いに答えよ。
(1)$b$を求めよ。$c$を$a$を用いて表せ。
(2)$C$が$x$軸と異なる2点で交わるとき、$\displaystyle\frac{1}{a}$のとりうる値の範囲を求めよ。
(3)$C$と$l_1$の接点をP、$C$と$l_2$の接点をQ、放物線$C$の頂点をRとする。$a$が(2)の条件を満たしながら動くとき、$\triangle PQR$の重心Gの軌跡を求めよ。
福田の数学〜大阪大学2024年文系第1問〜絶対値付き放物線と直線で囲まれた2つの面積が等しい条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 曲線$y$=|$x^2-1$|を$C$、直線$y$=$2a(x+1)$を$l$とする。ただし、$a$は0<$a$<1を満たす実数とする。
(1)曲線$C$と直線$l$の共有点の座標を全て求めよ。
(2)曲線$C$と直線$l$で囲まれた2つの部分の面積が等しくなる$a$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 曲線$y$=|$x^2-1$|を$C$、直線$y$=$2a(x+1)$を$l$とする。ただし、$a$は0<$a$<1を満たす実数とする。
(1)曲線$C$と直線$l$の共有点の座標を全て求めよ。
(2)曲線$C$と直線$l$で囲まれた2つの部分の面積が等しくなる$a$の値を求めよ。
#宮崎大学(2016)
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
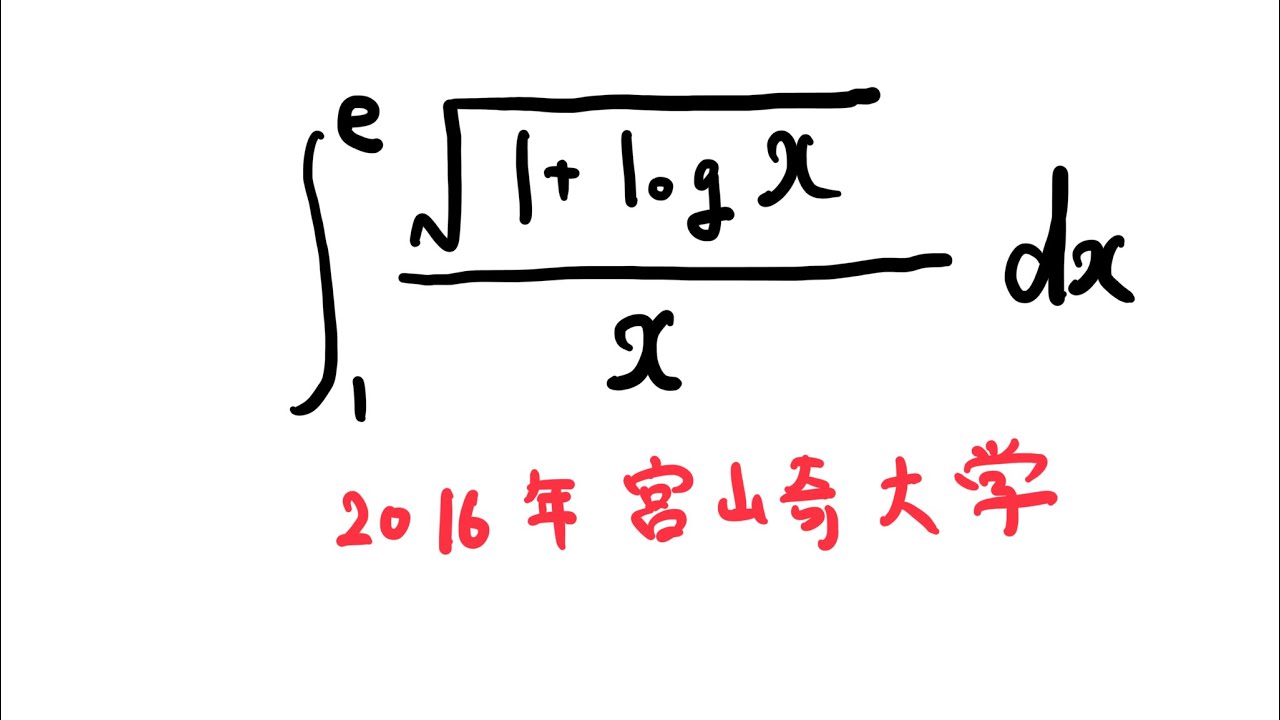
$\displaystyle \int_{1}^{e} \displaystyle \frac{\sqrt{ 1+log\ x }}{x} dx$
出典:2016年宮崎大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{\sqrt{ 1+log\ x }}{x} dx$
出典:2016年宮崎大学
#福島大学(2021) #定積分 #Shorts
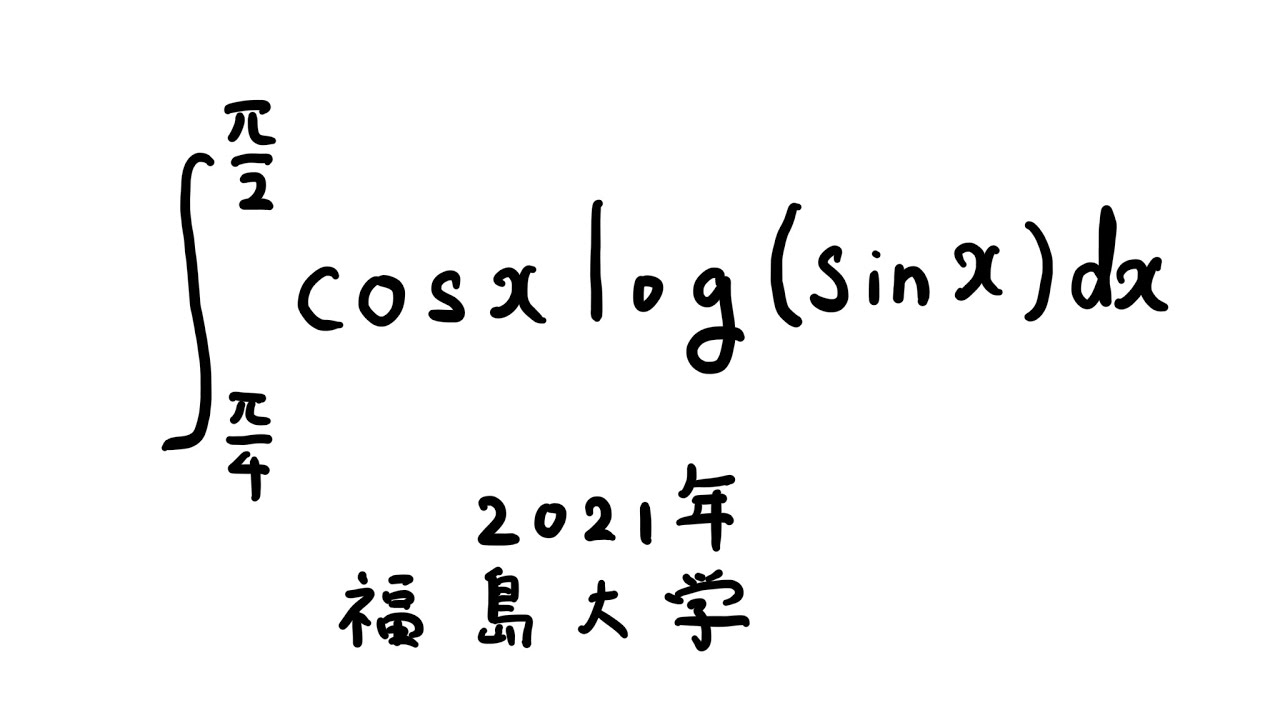
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典:2021年福島大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典:2021年福島大学
福田の数学〜慶應義塾大学2024年商学部第3問〜放物線と三角形の面積の最大

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $f(x)$=$\displaystyle-\frac{1}{8}x^2$+$5x$+18 とし、放物線$C$:$y$=$f(x)$と2つの直線$l_1$:$y$=$-x$, $l_2$:$y$=$x$ を考える。$C$と$l_1$の共有点のうち$x$座標が負のものをAとし、$C$と$l_2$の共有点のうち$x$座標が正のものをBとする。また、Aの$x$座標を$a$、Bの$x$座標を$b$とする。
(i)$a$=$\boxed{アイ}$-$\boxed{ウエ}\sqrt{\boxed{オ}}$, $a$=$\boxed{カキ}$である。
(ii)$C$と$l_2$で囲まれた部分のうち、$x$≧0の範囲にあるものの面積は$\boxed{クケコサ}$である。
以下、Pを$C$上の点とし、Pの$x$座標を$p$とする。またPにおける$C$の接線と$y$軸の交点をDとする。
(iii)$p$が0<$p$<$b$の範囲を動くとき、△ABPの面積が最大になるのは
$p$=$\boxed{シス}$-$\boxed{セ}\sqrt{\boxed{ソ}}$ のときである。
(iv)$p$=8 のとき、Dの$y$座標は$\boxed{タチ}$ である。
(v)$p$が0<$p$<$b$の範囲を動くとき、△BDPの面積$S$が最大になるのは
$p$=$\boxed{ツテ}$ のときであり、そのときの$S$は$\boxed{トナニ}$である。
この動画を見る
$\Large\boxed{3}$ $f(x)$=$\displaystyle-\frac{1}{8}x^2$+$5x$+18 とし、放物線$C$:$y$=$f(x)$と2つの直線$l_1$:$y$=$-x$, $l_2$:$y$=$x$ を考える。$C$と$l_1$の共有点のうち$x$座標が負のものをAとし、$C$と$l_2$の共有点のうち$x$座標が正のものをBとする。また、Aの$x$座標を$a$、Bの$x$座標を$b$とする。
(i)$a$=$\boxed{アイ}$-$\boxed{ウエ}\sqrt{\boxed{オ}}$, $a$=$\boxed{カキ}$である。
(ii)$C$と$l_2$で囲まれた部分のうち、$x$≧0の範囲にあるものの面積は$\boxed{クケコサ}$である。
以下、Pを$C$上の点とし、Pの$x$座標を$p$とする。またPにおける$C$の接線と$y$軸の交点をDとする。
(iii)$p$が0<$p$<$b$の範囲を動くとき、△ABPの面積が最大になるのは
$p$=$\boxed{シス}$-$\boxed{セ}\sqrt{\boxed{ソ}}$ のときである。
(iv)$p$=8 のとき、Dの$y$座標は$\boxed{タチ}$ である。
(v)$p$が0<$p$<$b$の範囲を動くとき、△BDPの面積$S$が最大になるのは
$p$=$\boxed{ツテ}$ のときであり、そのときの$S$は$\boxed{トナニ}$である。
#筑波大学(2016) #定積分 #Shorts
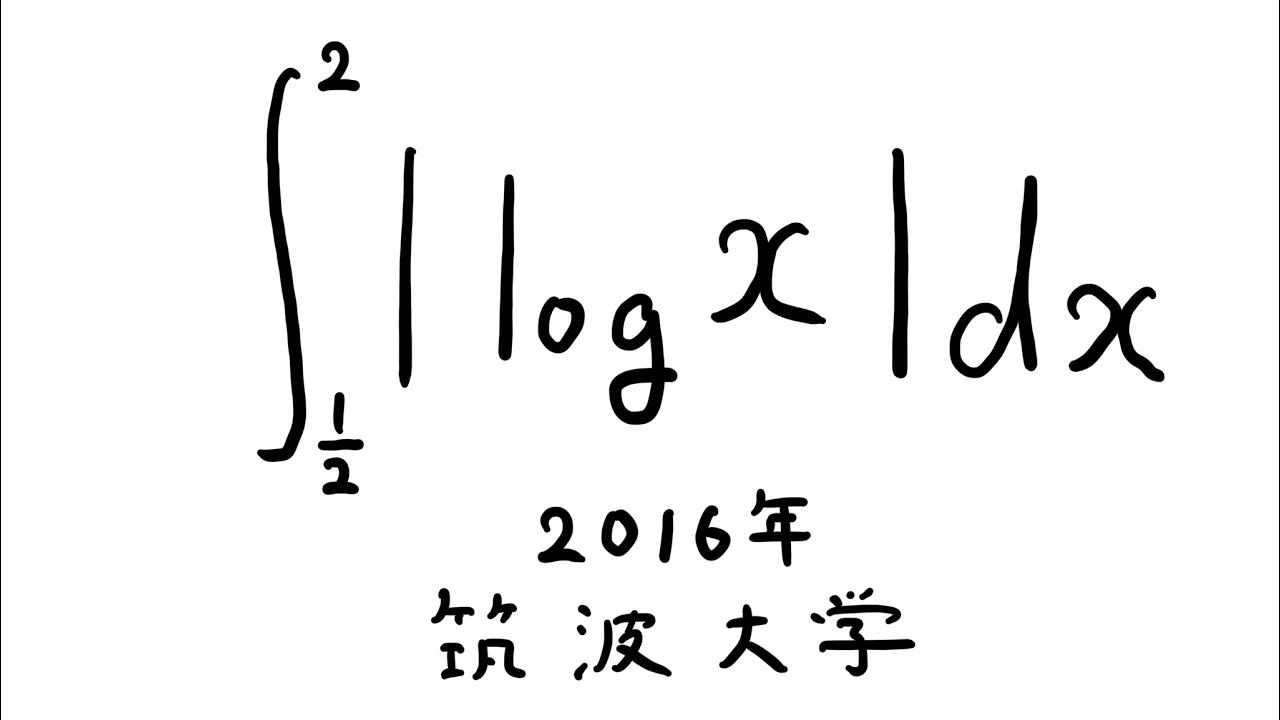
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{2}}^{2} |log\ x| dx$
出典:2016年筑波大学
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{2} |log\ x| dx$
出典:2016年筑波大学
大学入試問題#825「まあまあ良問」 #茨城大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-7}^{1}(2-x) \sqrt[ 3 ]{ 1-x }\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{-7}^{1}(2-x) \sqrt[ 3 ]{ 1-x }\ dx$
出典:2022年茨城大学
#秋田大学(2019) #定積分 #Shorts
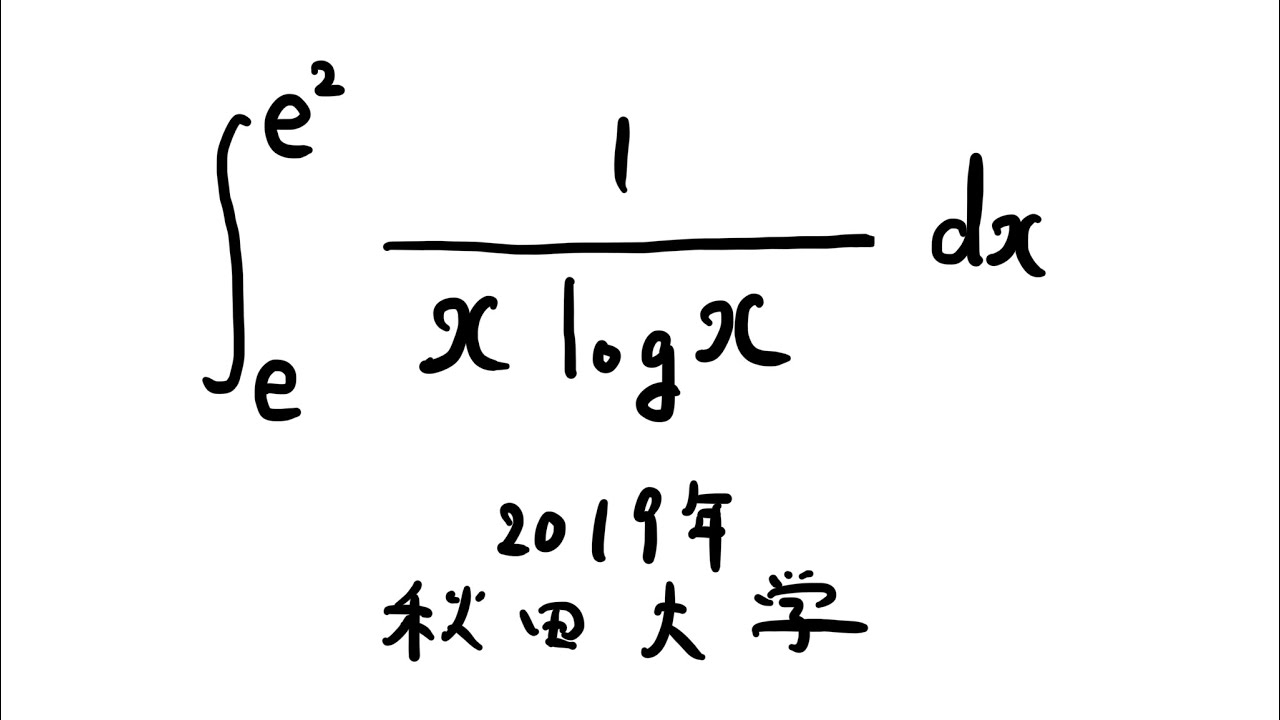
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#秋田大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{1}{x\ log\ x} dx$
出典:2019年秋田大学
この動画を見る
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{1}{x\ log\ x} dx$
出典:2019年秋田大学
大学入試問題#824「たぶん良問」 #筑波大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2-2x-2}{x^3-1} dx$
出典:2022年筑波大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2-2x-2}{x^3-1} dx$
出典:2022年筑波大学
#茨城大学(2023) #定積分 #Shorts
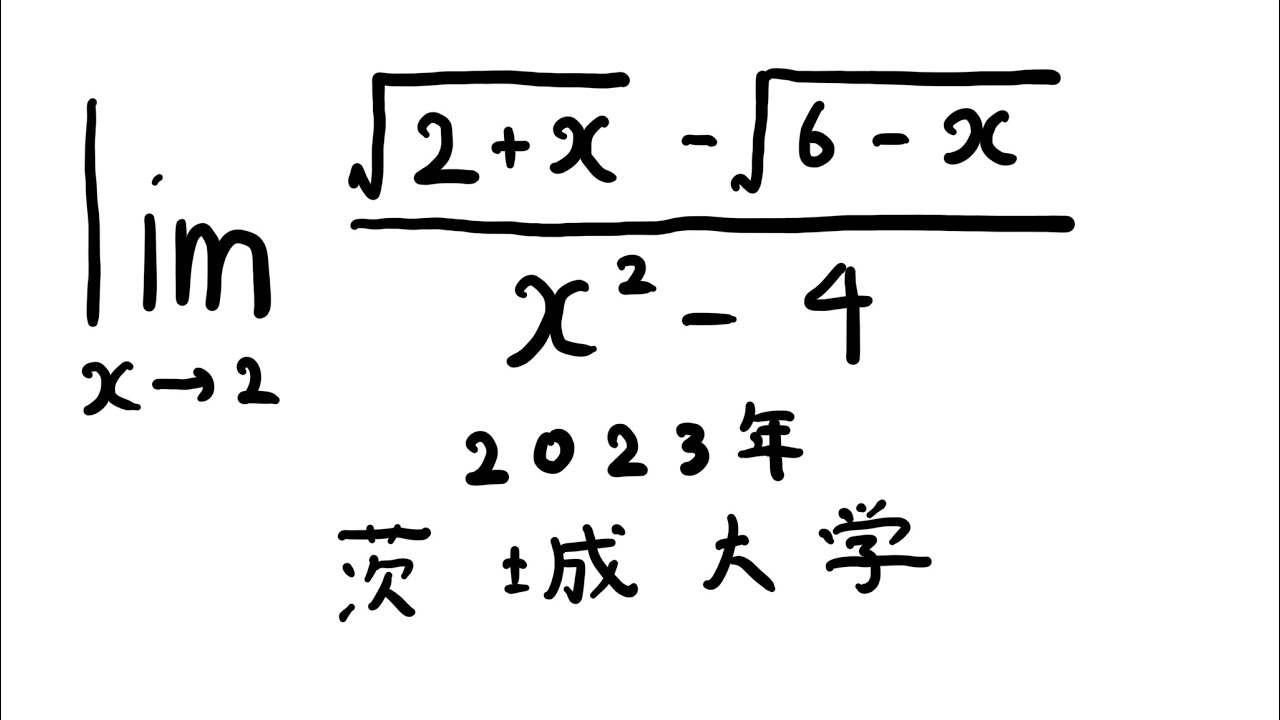
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 2 } \displaystyle \frac{\sqrt{ 2+x }-\sqrt{ 6-x }}{x^2-4}$
出典:2023年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to 2 } \displaystyle \frac{\sqrt{ 2+x }-\sqrt{ 6-x }}{x^2-4}$
出典:2023年茨城大学
#茨城大学(2022) #定積分 #Shorts
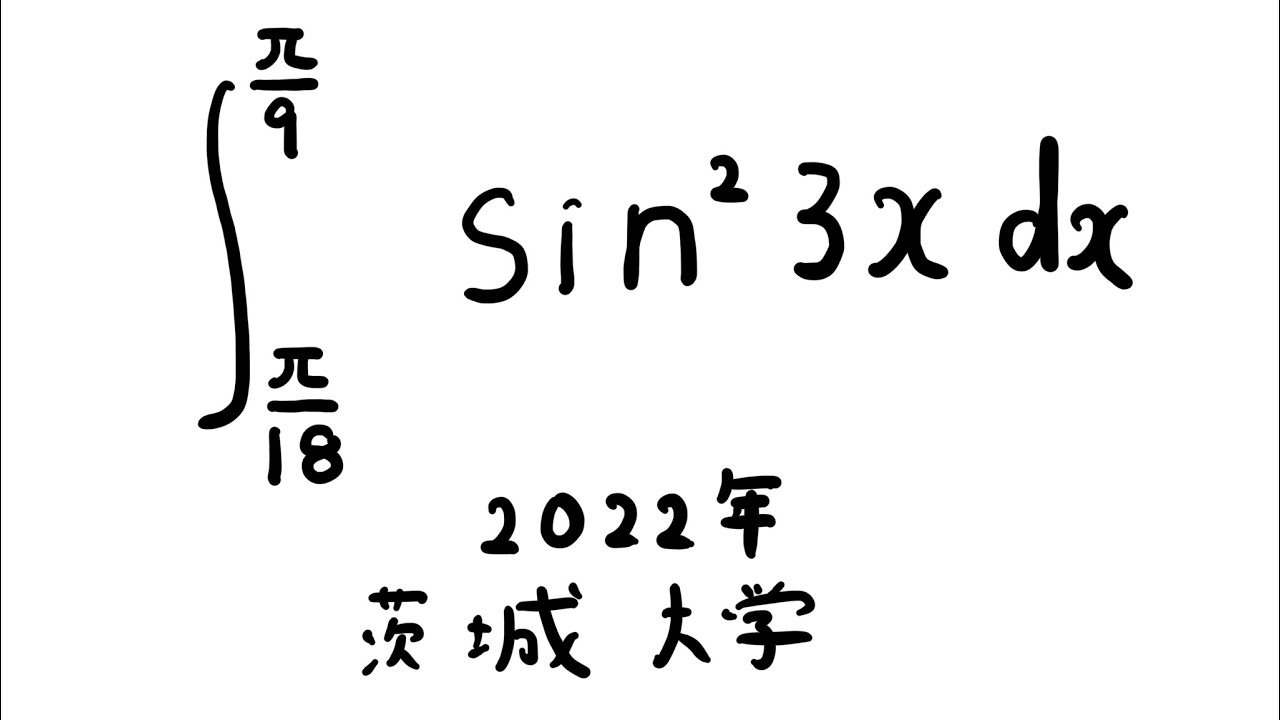
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{18}}^{\frac{\pi}{9}} \sin^23x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{18}}^{\frac{\pi}{9}} \sin^23x\ dx$
出典:2022年茨城大学
大学入試問題#823「置換するかどうか」 #筑波大学(2019) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (x+1)^2e-(x+1) dx$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} (x+1)^2e-(x+1) dx$
出典:2019年筑波大学
#茨城大学(2022) #定積分 #Shorts
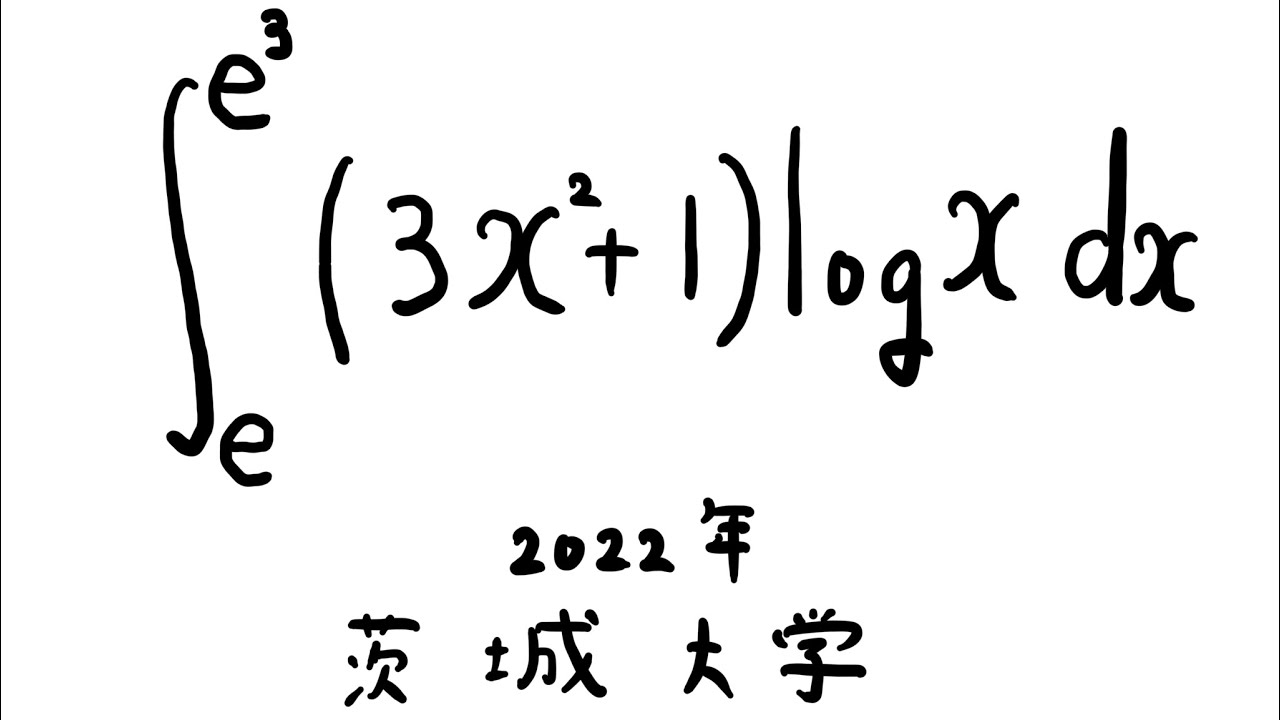
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^3} (3x^2+1)log\ x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{e}^{e^3} (3x^2+1)log\ x\ dx$
出典:2022年茨城大学
#茨城大学(2022) #定積分 #Shorts
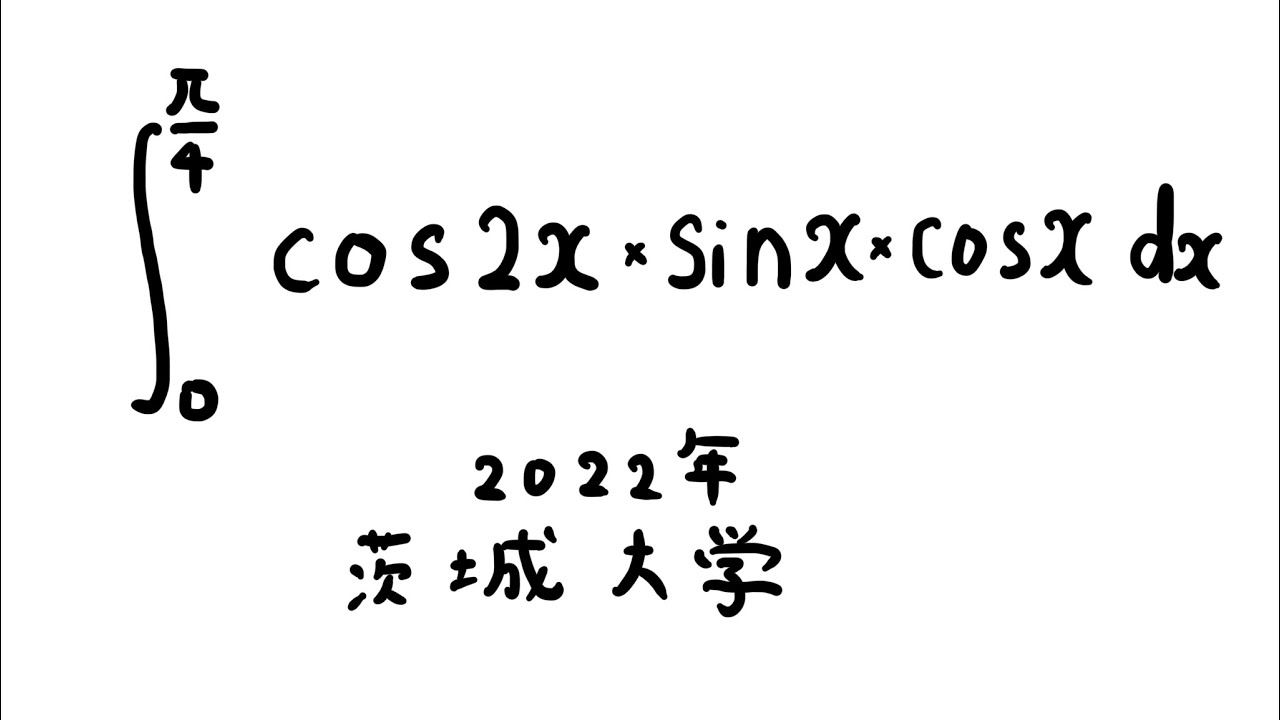
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos2x\times\sin\ x\ cos\ x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos2x\times\sin\ x\ cos\ x\ dx$
出典:2022年茨城大学
大学入試問題#822「これ、積分で出題されるんやー」 #筑波大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(x+\sqrt{ x^2+1 }) dx$
出典:2022年筑波大学
この動画を見る
$\displaystyle \int log(x+\sqrt{ x^2+1 }) dx$
出典:2022年筑波大学
#茨城大学(2023) #定積分 #Shorts
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
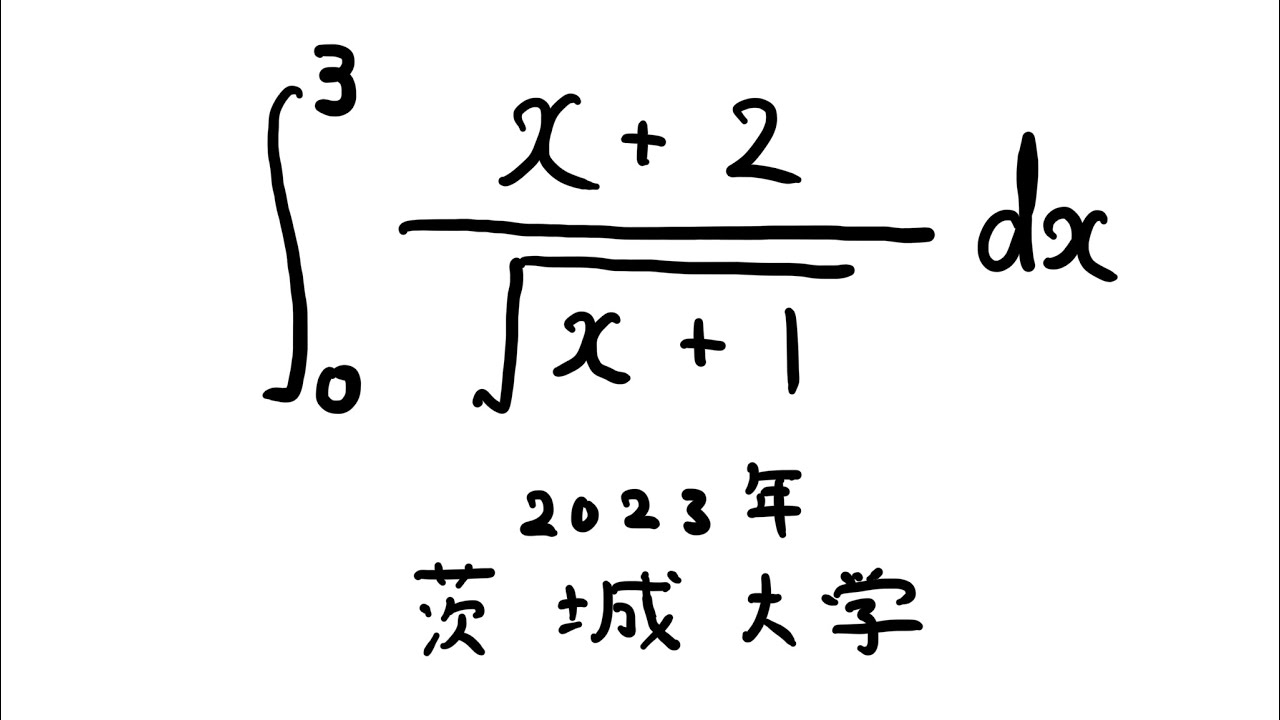
$\displaystyle \int_{0}^{3} \displaystyle \frac{x+2}{\sqrt{ x+1 }} dx$
出典:2023年茨城大学
この動画を見る
$\displaystyle \int_{0}^{3} \displaystyle \frac{x+2}{\sqrt{ x+1 }} dx$
出典:2023年茨城大学
#奈良教育大学(2008) #定積分 #Shorts
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
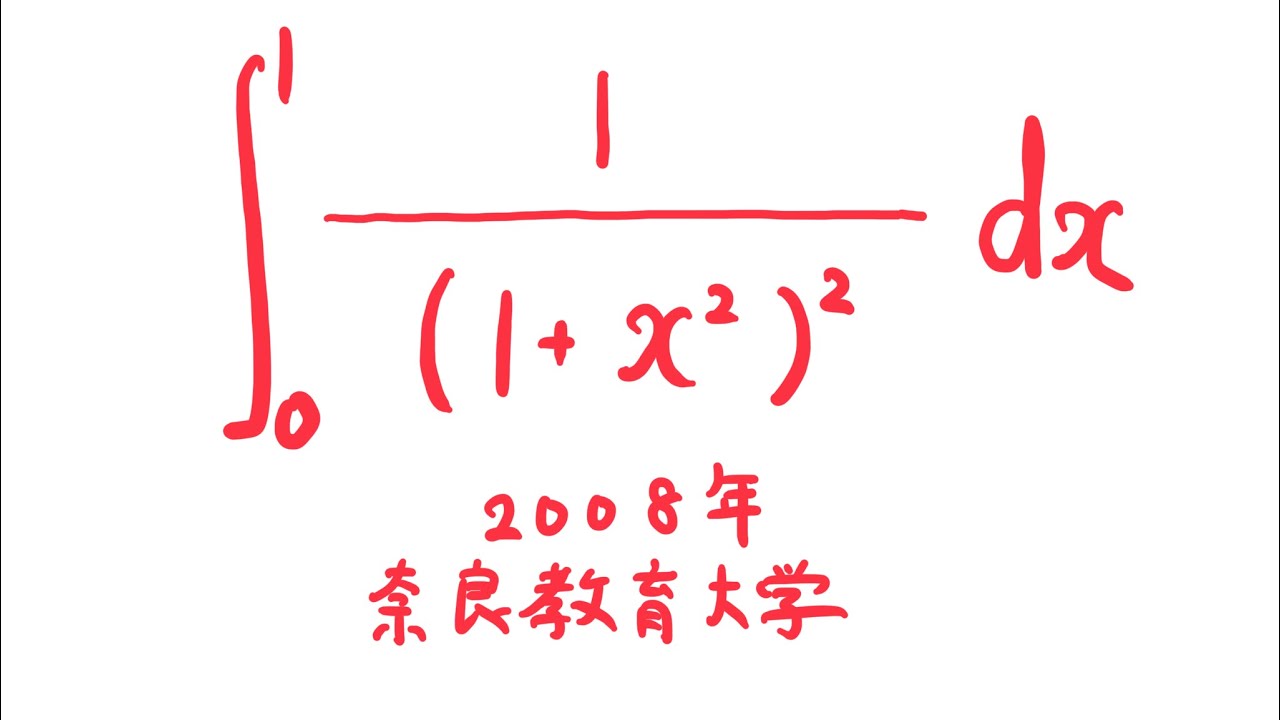
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^2} dx$
出典:2008年奈良教育大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^2} dx$
出典:2008年奈良教育大学
#筑波大学(2020) #定積分 #Shorts
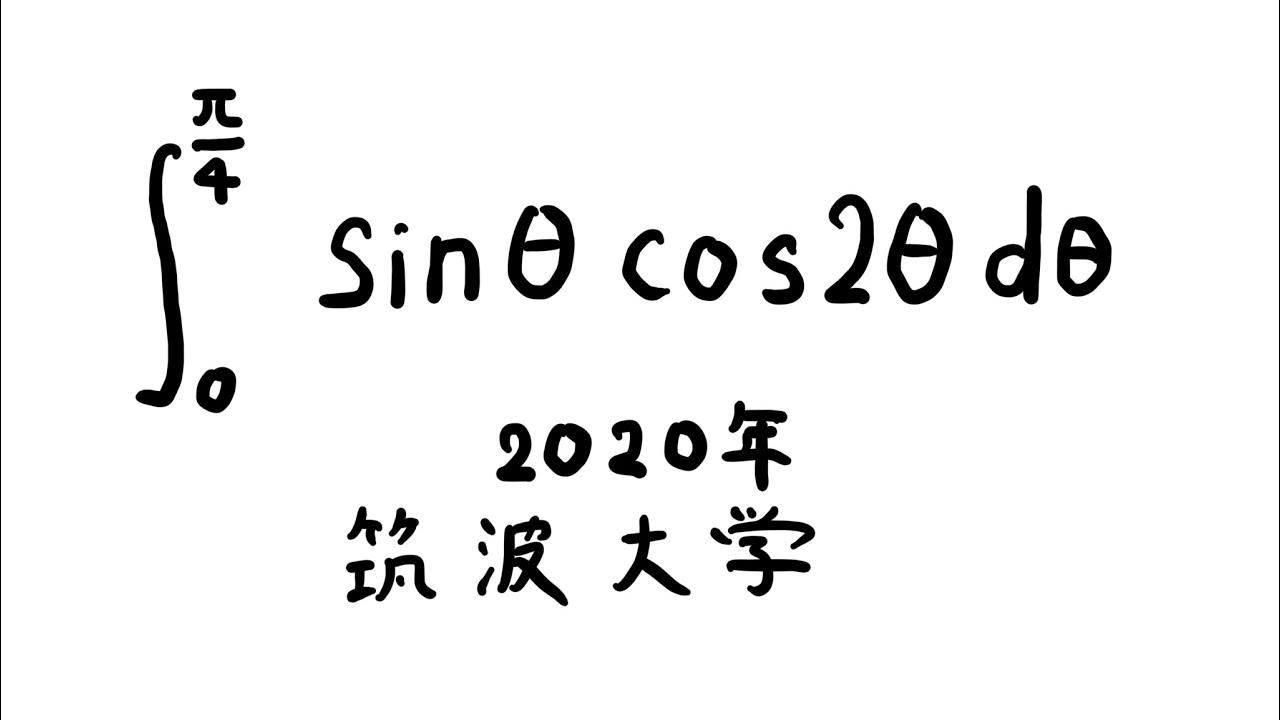
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin\theta\ \cos2\theta\ d\theta$
出典:2020年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin\theta\ \cos2\theta\ d\theta$
出典:2020年筑波大学
大学入試問題#821「王道問題」 #筑波大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} \displaystyle \frac{2x+3}{x^2+2x+4} dx$
出典:2022年筑波大学
この動画を見る
$\displaystyle \int_{0}^{2} \displaystyle \frac{2x+3}{x^2+2x+4} dx$
出典:2022年筑波大学
#茨城大学(2023) #定積分 #Shorts
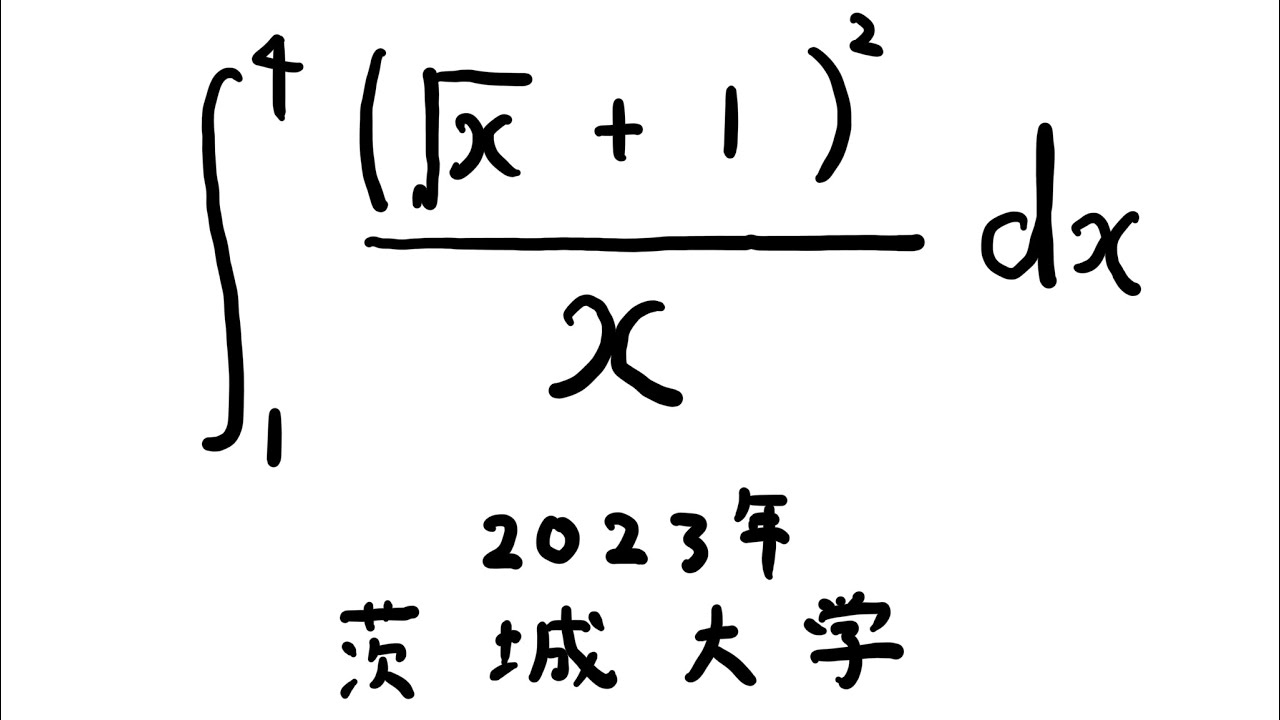
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4} \displaystyle \frac{(\sqrt{ x }+1)^2}{x} dx$
出典:2023年茨城大学
この動画を見る
$\displaystyle \int_{1}^{4} \displaystyle \frac{(\sqrt{ x }+1)^2}{x} dx$
出典:2023年茨城大学
#奈良教育大学(2014) #定積分 #Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} |e^x-e| dx$
出典:2014年奈良教育大学
この動画を見る
$\displaystyle \int_{0}^{2} |e^x-e| dx$
出典:2014年奈良教育大学
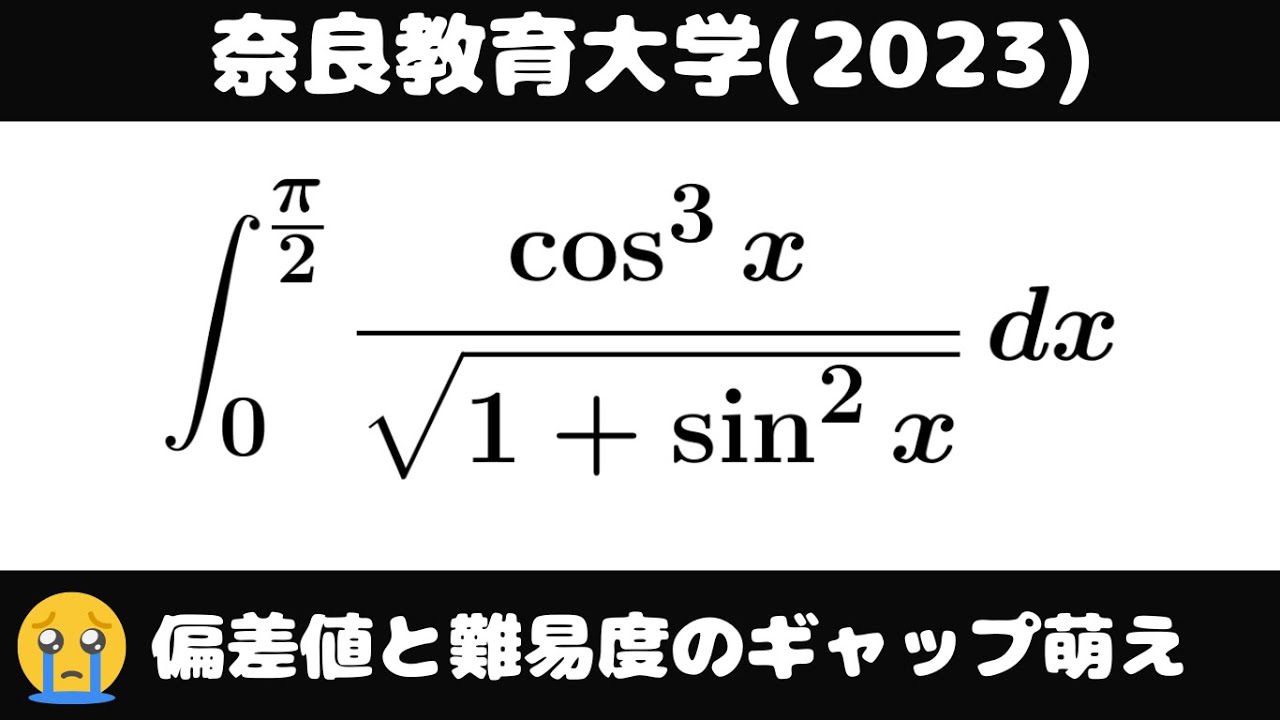
大学入試問題#820「初手は見えるが、次の手は?」 #奈良教育大学(2023) #定積分
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos^3\ x}{\sqrt{ 1+\sin^2 }} dx$
出典:2023年奈良教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos^3\ x}{\sqrt{ 1+\sin^2 }} dx$
出典:2023年奈良教育大学 入試問題
福田の数学〜慶應義塾大学2024年商学部第1問(2)〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(2)等式 $f(x)$=$12x^2$+$\displaystyle 6x\int_0^1f(t)dt$+$\displaystyle 2\int_0^1tf(t)dt$ を満たす関数$f(x)$を求めよ。
この動画を見る
$\Large\boxed{1}$
(2)等式 $f(x)$=$12x^2$+$\displaystyle 6x\int_0^1f(t)dt$+$\displaystyle 2\int_0^1tf(t)dt$ を満たす関数$f(x)$を求めよ。
#茨城大学(2020) #定積分 #Shorts
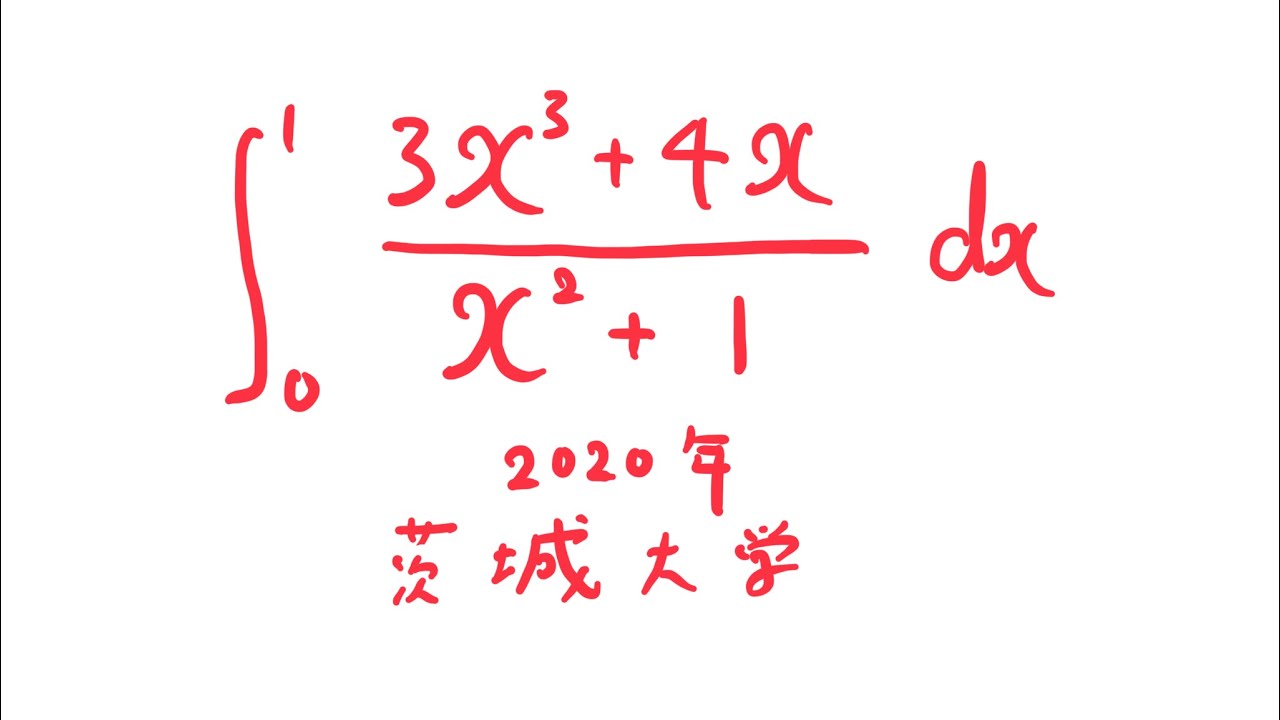
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
#筑波大学(2018) #定積分 #Shorts
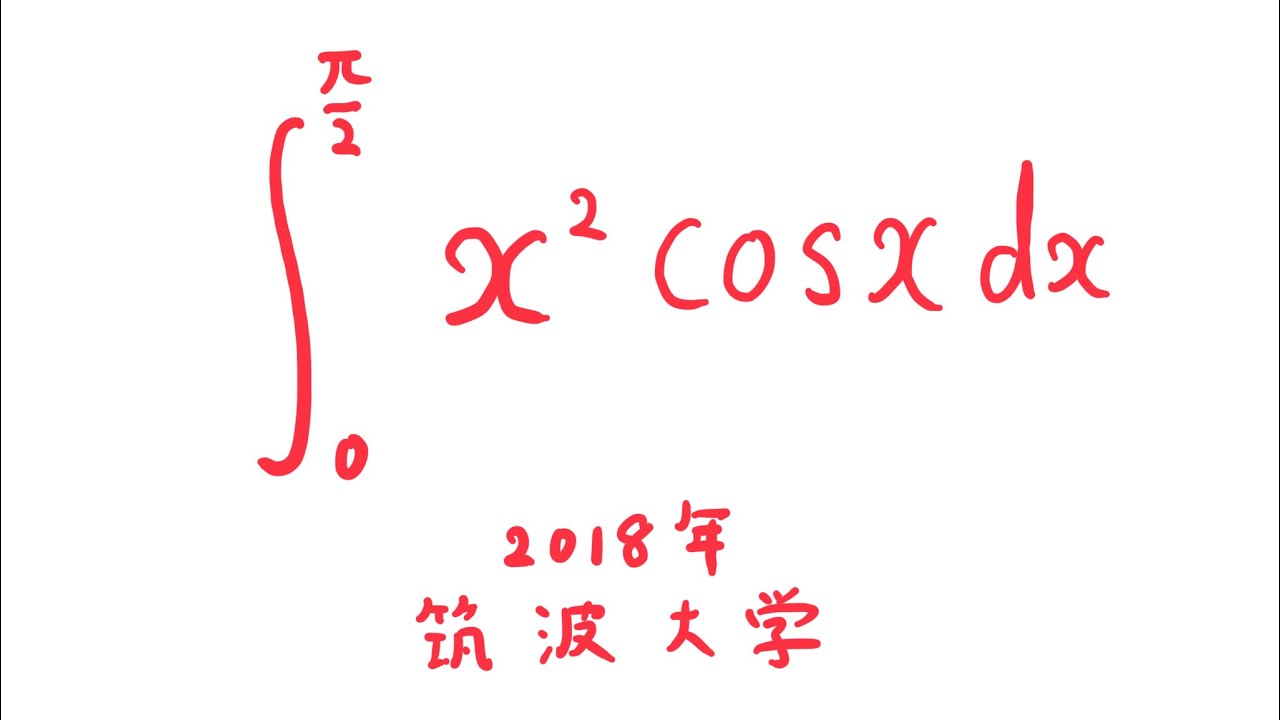
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} x^2\cos\ x\ dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} x^2\cos\ x\ dx$
出典:2018年筑波大学
大学入試問題#819「楽に計算したい」 #奈良教育大学(2009) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=\cos\ x+2\displaystyle \int_{0}^{\frac{\pi}{2}} tf(t) \sin\ t\ dt$
出典:2009年奈良教育大学
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=\cos\ x+2\displaystyle \int_{0}^{\frac{\pi}{2}} tf(t) \sin\ t\ dt$
出典:2009年奈良教育大学
#筑波大学(2019) #定積分 #Shorts
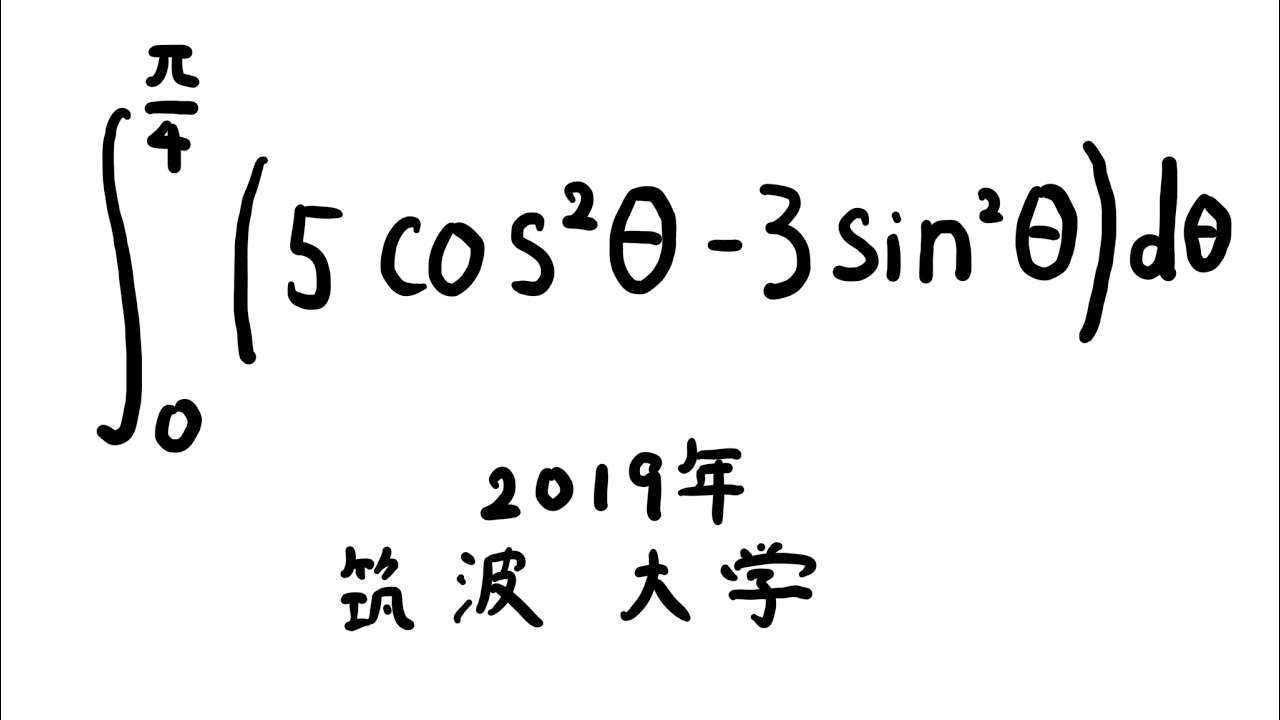
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} (5\cos^2\theta-3\sin^2\theta)d\theta$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} (5\cos^2\theta-3\sin^2\theta)d\theta$
出典:2019年筑波大学
福田の数学〜早稲田大学2024年理工学部第5問〜媒介変数表示のグラフと回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#積分とその応用#微分法#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $xy$平面上において、以下の媒介変数表示をもつ曲線を$C$とする。
$\left\{\begin{array}{1}
x=\sin t+\displaystyle\frac{1}{2}\sin 2t \\
y=-\cos t-\displaystyle\frac{1}{2}\cos 2t-\frac{1}{2}\\
\end{array}\right.
$
ただし、0≦$t$≦$\pi$とする。
(1)$y$の最大値、最小値を求めよ。
(2)$\displaystyle\frac{dy}{dt}$<0 となる$t$の範囲を求め、$C$の概形を$xy$平面上に描け。
(3)$C$を$y$軸のまわりに1回転してできる立体の体積$V$を求めよ。
この動画を見る
$\Large\boxed{5}$ $xy$平面上において、以下の媒介変数表示をもつ曲線を$C$とする。
$\left\{\begin{array}{1}
x=\sin t+\displaystyle\frac{1}{2}\sin 2t \\
y=-\cos t-\displaystyle\frac{1}{2}\cos 2t-\frac{1}{2}\\
\end{array}\right.
$
ただし、0≦$t$≦$\pi$とする。
(1)$y$の最大値、最小値を求めよ。
(2)$\displaystyle\frac{dy}{dt}$<0 となる$t$の範囲を求め、$C$の概形を$xy$平面上に描け。
(3)$C$を$y$軸のまわりに1回転してできる立体の体積$V$を求めよ。
#筑波大学(2019) #定積分 #Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
#奈良教育大学(2014) #定積分 #Shorts
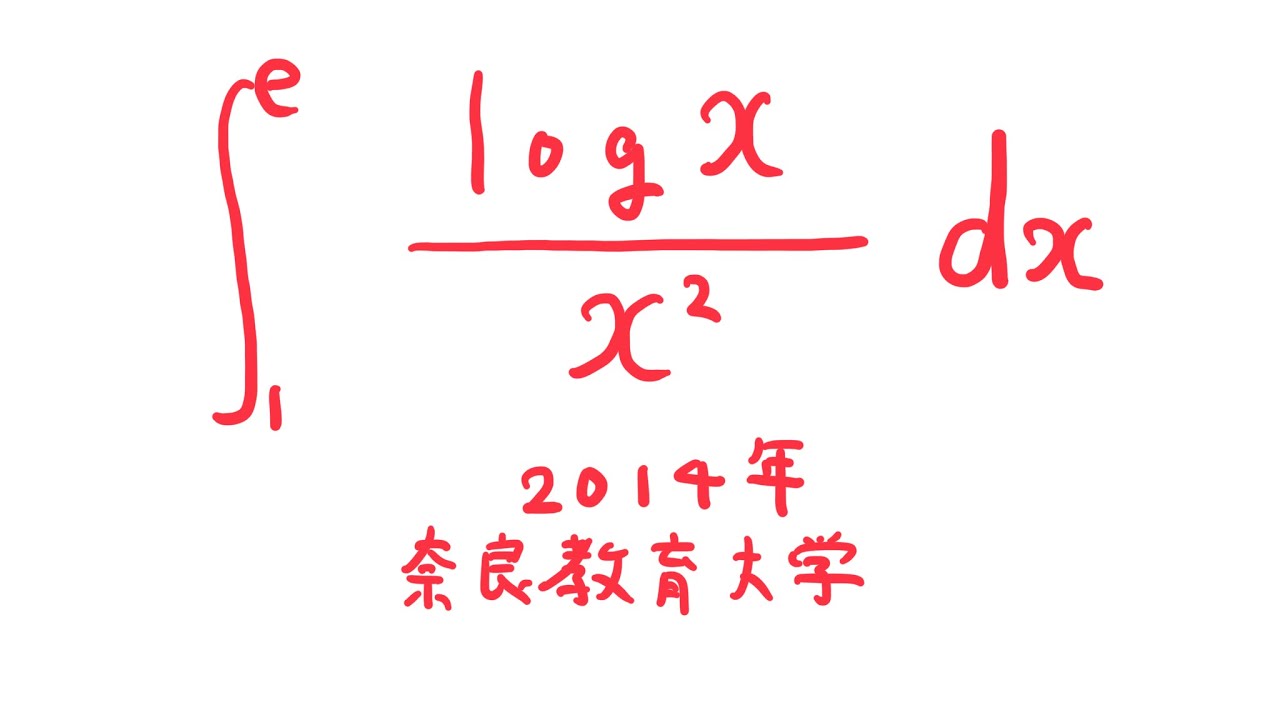
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
