 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
福田のわかった数学〜高校2年生061〜対称式と領域(3)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 対称式と領域(3)
実数$x,\ y$が$x^2+xy+y^2=6$を
満たしながら動くとき
$x^2y+xy^2-x^2-2xy-y^2+x+y$
の取り得る値の範囲を求めよ。
この動画を見る
数学$\textrm{II}$ 対称式と領域(3)
実数$x,\ y$が$x^2+xy+y^2=6$を
満たしながら動くとき
$x^2y+xy^2-x^2-2xy-y^2+x+y$
の取り得る値の範囲を求めよ。
福田の数学〜明治大学2021年全学部統一入試IⅡAB第2問〜2つのグラフの共有点の個数と面積

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#微分法と積分法#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
大学入試問題#924「定場の問題」 #岡山県立大学2023

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} (8\cos^4-8\cos^2 x+1)dx$
を解け.
2023岡山県立大学過去問題
この動画を見る
$\displaystyle \int_{}^{} (8\cos^4-8\cos^2 x+1)dx$
を解け.
2023岡山県立大学過去問題
#関西大学2024#不定積分_36
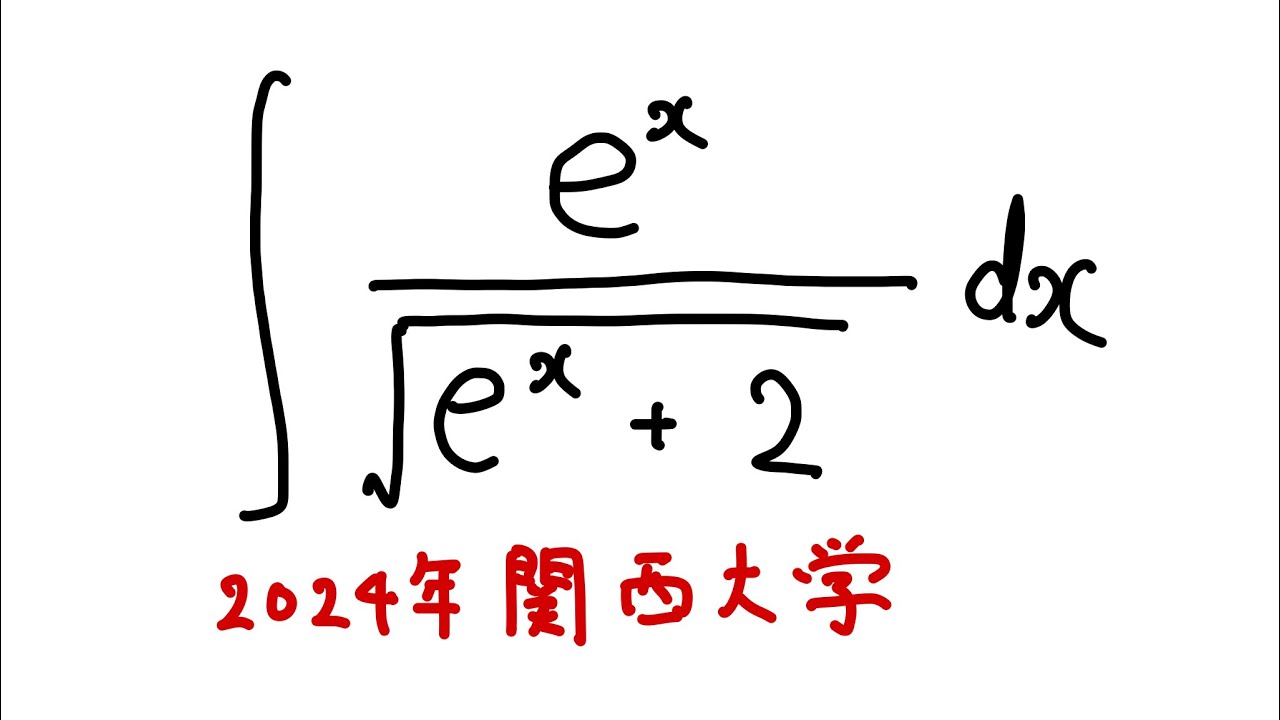
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{e^x}{\sqrt{e^x+2}}dx$
を解け.
2024関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{e^x}{\sqrt{e^x+2}}dx$
を解け.
2024関西大学過去問題
#関西大学2024#不定積分_35

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{x^3+2x}{x^2+1} dx$
を解け.
2024関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^3+2x}{x^2+1} dx$
を解け.
2024関西大学過去問題
【数Ⅱ】積分法:2次関数の面積を半分にする1次関数

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線y=-x(x-6)とx軸で囲まれた図形の面積を、直線y=mxが2等分するとき、定数mの値を求めよう。
この動画を見る
放物線y=-x(x-6)とx軸で囲まれた図形の面積を、直線y=mxが2等分するとき、定数mの値を求めよう。
福田の数学〜上智大学2021年TEAP利用文系第3問〜反復試行の確率と3次関数の極大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$硬貨を2枚投げる試行を3回繰り返して、1回目、2回目、3回目に出た表の枚数
を順に$\alpha,\beta,\gamma$とする。3次関数
$f(x)=(x-\alpha)(x-\beta)(x-\gamma)$
を考える。
(1)関数$y=f(x)$が極値をとらない確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(2)関数$y=f(x)$が極大値をとるとき、その極大値の取り得る値のうち最小のもの
は$\boxed{\ \ ニ\ \ }$で、最大のものは$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$である。
(3)関数$y=f(x)$が極大値$\boxed{\ \ ニ\ \ }$をとる確率は$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。
(4)関数$y=f(x)$が極大値$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$を取る確率は$\frac{\boxed{\ \ ヒ\ \ }}{\boxed{\ \ フ\ \ }}$である。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{3}}$硬貨を2枚投げる試行を3回繰り返して、1回目、2回目、3回目に出た表の枚数
を順に$\alpha,\beta,\gamma$とする。3次関数
$f(x)=(x-\alpha)(x-\beta)(x-\gamma)$
を考える。
(1)関数$y=f(x)$が極値をとらない確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(2)関数$y=f(x)$が極大値をとるとき、その極大値の取り得る値のうち最小のもの
は$\boxed{\ \ ニ\ \ }$で、最大のものは$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$である。
(3)関数$y=f(x)$が極大値$\boxed{\ \ ニ\ \ }$をとる確率は$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。
(4)関数$y=f(x)$が極大値$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$を取る確率は$\frac{\boxed{\ \ ヒ\ \ }}{\boxed{\ \ フ\ \ }}$である。
2021上智大学文系過去問
06和歌山県教員採用試験(数学:3番 定積分の応用)
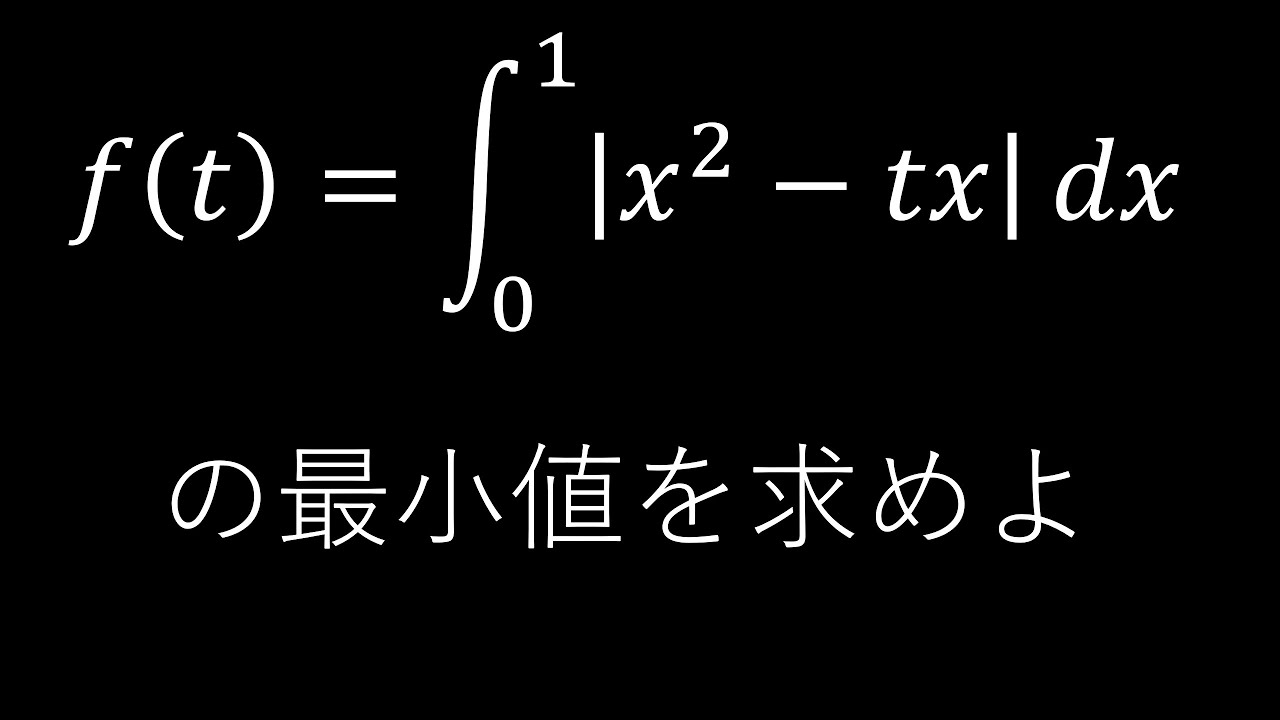
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(t)=\displaystyle \int_{0}^{1}|x^2-tx|dx$の最小値を求めよ。
出典:和歌山県教員採用試験
この動画を見る
$f(t)=\displaystyle \int_{0}^{1}|x^2-tx|dx$の最小値を求めよ。
出典:和歌山県教員採用試験
福田の数学〜上智大学2021年TEAP利用文系第2問〜放物線の接線と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$xy平面において、放物線$C:y=x^2$と、互いに直交するCの2つの接線l,mを
考える。
(1)lが点$(2,\ 4)$を通るとき、mの方程式は
$y=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\ x+\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$
であり、lとmの交点の座標は
$(\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }},\ \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }})$
である。
(2)lとmの交点がy軸上にあるとき、2直線l,mとCの囲む図形の面積は$\frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}$である。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{2}}$xy平面において、放物線$C:y=x^2$と、互いに直交するCの2つの接線l,mを
考える。
(1)lが点$(2,\ 4)$を通るとき、mの方程式は
$y=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\ x+\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$
であり、lとmの交点の座標は
$(\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }},\ \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }})$
である。
(2)lとmの交点がy軸上にあるとき、2直線l,mとCの囲む図形の面積は$\frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}$である。
2021上智大学文系過去問
福田の数学〜中央大学2021年経済学部第1問(6)〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(6)次の2つの等式を満たす関数f(x)を求めよ。
$f(0)=-\frac{1}{3}, f'(x)=2x+\int_0^1f(t)dt$
2021中央大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(6)次の2つの等式を満たす関数f(x)を求めよ。
$f(0)=-\frac{1}{3}, f'(x)=2x+\int_0^1f(t)dt$
2021中央大学経済学部過去問
東大 大島さんと数学 球の体積

福田の数学〜中央大学2021年理工学部第1問〜斜回転

単元:
#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$放物線$C:y=x^2$上の点$(a,\ a^2)$ $(a \gt 0)$における法線lの方程式を$y=f(x)$
とおくと、$f(x)=\boxed{\ \ ア\ \ }$となる。またCとlの交点のうちPと異なる方の点Qを
求めると、$Q(\boxed{\ \ イ\ \ },\ \boxed{\ \ イ\ \ }^2)$となる。以下、Cとlで囲まれた部分をDとし、
Dをlの周りに1回転して得られる回転体の体積$V(a)$を求める。Dに含まれるl上
の点を$R(t,\ f(t))$ $(\boxed{\ \ イ\ \ }$ $\leqq t \leqq a)$とおく。Rを通りlに垂直な直線は
$y=2a(x-t)+f(t)$で与えられる。この直線と$y=x^2$の2つの交点のうち
Dに含まれる方の点Sのx座標は$x=a-\boxed{\ \ ウ\ \ }\sqrt{a-t}$ となる。このとき
線分RSの長さ$r=g(t)$は$g(t)=\boxed{\ \ エ\ \ }(t-a+\boxed{\ \ ウ\ \ }\sqrt{a-t})$となる。
線分QRの長さ$s=h(t)$は$h(t)=\boxed{\ \ オ\ \ }(t-\boxed{\ \ イ\ \ })$で与えられるので、
$V(a)=\pi\int_0^{h(a)}r^2ds=\pi\int_{\boxed{イ}}^a\left\{g(t)\right\}^2h'(t)dt$
$=\pi\left\{(\boxed{\ \ エ\ \ })^2×\boxed{\ \ オ\ \ }\right\}\int_{\boxed{イ}}^a(a-t)(-\sqrt{a-t}+\boxed{\ \ ウ\ \ })^2dt$
となる。ここで$u=\sqrt{a-t}$とおいて置換積分を行えば
$V(a)=2\pi\left\{(\boxed{\ \ エ\ \ })^2×\boxed{\ \ オ\ \ }\right\}\int_0^{\boxed{ウ}}\left\{u^5-2\boxed{\ \ ウ\ \ }u^4+(\boxed{\ \ ウ\ \ })^2u^3\right\}du=\boxed{\ \ カ\ \ }$
が求まる。さらに、$a \gt 0$の範囲で$a$を動かすとき、$\lim_{a \to +0}V(a)=\lim_{a \to \infty}V(a)=\infty$
であり、$V(a)$を最小にするaの値は$a=\boxed{\ \ キ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
ⓐ$-\frac{2}{a}(x-a)+a^2$ ⓑ$-\frac{1}{a}(x-a)+a^2$ ⓒ$-\frac{1}{2a}(x-a)+a^2$ ⓓ$-2a(x-a)+a^2$
$\boxed{\ \ イ\ \ }~\ \boxed{\ \ オ\ \ }$の解答群
ⓐ$-\frac{a^2-1}{a}$ ⓑ$-\frac{2a^2-1}{2a}$ ⓒ$-\frac{a^2+1}{a}$ ⓓ$-\frac{2a^2+1}{2a}$
ⓔ$\frac{\sqrt{a^2+4}}{2}$ ⓕ$\sqrt{a^2+1}$ ⓖ$\sqrt{4a^2+1}$ ⓗ$2a$
ⓘ$\frac{\sqrt{4a^2+1}}{2a}$ ⓙ$\frac{\sqrt{a^2+4}}{a}$ ⓚ$\frac{\sqrt{a^2+1}}{a}$ ⓛ$\frac{\sqrt{a^2+1}}{2a}$
ⓜ$\sqrt{\frac{2a^2+1}{2a}}$ ⓝ$\sqrt{\frac{4a^2+1}{2a}}$ ⓞ$\sqrt{\frac{2a^2+1}{a}}$ ⓟ$\sqrt{\frac{4a^2+1}{a}}$
$\boxed{\ \ カ\ \ }$の解答群
$ⓐ\frac{(2a^2+1)^3(a^2+1)^{\frac{3}{2}}}{60a^4}\ \pi ⓑ\frac{(2a^2+1)^{\frac{9}{2}}}{120a^4}\ \pi ⓒ\frac{(2a^2+1)^{\frac{9}{2}}}{60a^4}\ \pi$
$ⓓ\frac{(2a^2+1)^3(4a^2+1)^{\frac{3}{2}}}{60a^4}\ \pi ⓔ\frac{(4a^2+1)^{\frac{9}{2}}}{480a^4}\ \pi ⓕ\frac{(4a^2+1)^{\frac{9}{2}}}{60a^4}\ \pi$
$ⓖ\frac{(a^2+1)^2(4a^2+1)^2}{120a^{\frac{7}{2}}}\ \pi ⓗ\frac{(4a^2+1)^4}{480\sqrt2a^{\frac{7}{2}}}\ \pi ⓘ\frac{(4a^2+1)^4}{120\sqrt2a^{\frac{7}{2}}}\ \pi$
$\boxed{\ \ キ\ \ }$の解答群
$ⓐ\frac{1}{\sqrt5} ⓑ\frac{1}{\sqrt2} ⓒ1 ⓓ\sqrt2 ⓔ\frac{2}{\sqrt5} ⓕ4$
2021中央大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$放物線$C:y=x^2$上の点$(a,\ a^2)$ $(a \gt 0)$における法線lの方程式を$y=f(x)$
とおくと、$f(x)=\boxed{\ \ ア\ \ }$となる。またCとlの交点のうちPと異なる方の点Qを
求めると、$Q(\boxed{\ \ イ\ \ },\ \boxed{\ \ イ\ \ }^2)$となる。以下、Cとlで囲まれた部分をDとし、
Dをlの周りに1回転して得られる回転体の体積$V(a)$を求める。Dに含まれるl上
の点を$R(t,\ f(t))$ $(\boxed{\ \ イ\ \ }$ $\leqq t \leqq a)$とおく。Rを通りlに垂直な直線は
$y=2a(x-t)+f(t)$で与えられる。この直線と$y=x^2$の2つの交点のうち
Dに含まれる方の点Sのx座標は$x=a-\boxed{\ \ ウ\ \ }\sqrt{a-t}$ となる。このとき
線分RSの長さ$r=g(t)$は$g(t)=\boxed{\ \ エ\ \ }(t-a+\boxed{\ \ ウ\ \ }\sqrt{a-t})$となる。
線分QRの長さ$s=h(t)$は$h(t)=\boxed{\ \ オ\ \ }(t-\boxed{\ \ イ\ \ })$で与えられるので、
$V(a)=\pi\int_0^{h(a)}r^2ds=\pi\int_{\boxed{イ}}^a\left\{g(t)\right\}^2h'(t)dt$
$=\pi\left\{(\boxed{\ \ エ\ \ })^2×\boxed{\ \ オ\ \ }\right\}\int_{\boxed{イ}}^a(a-t)(-\sqrt{a-t}+\boxed{\ \ ウ\ \ })^2dt$
となる。ここで$u=\sqrt{a-t}$とおいて置換積分を行えば
$V(a)=2\pi\left\{(\boxed{\ \ エ\ \ })^2×\boxed{\ \ オ\ \ }\right\}\int_0^{\boxed{ウ}}\left\{u^5-2\boxed{\ \ ウ\ \ }u^4+(\boxed{\ \ ウ\ \ })^2u^3\right\}du=\boxed{\ \ カ\ \ }$
が求まる。さらに、$a \gt 0$の範囲で$a$を動かすとき、$\lim_{a \to +0}V(a)=\lim_{a \to \infty}V(a)=\infty$
であり、$V(a)$を最小にするaの値は$a=\boxed{\ \ キ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
ⓐ$-\frac{2}{a}(x-a)+a^2$ ⓑ$-\frac{1}{a}(x-a)+a^2$ ⓒ$-\frac{1}{2a}(x-a)+a^2$ ⓓ$-2a(x-a)+a^2$
$\boxed{\ \ イ\ \ }~\ \boxed{\ \ オ\ \ }$の解答群
ⓐ$-\frac{a^2-1}{a}$ ⓑ$-\frac{2a^2-1}{2a}$ ⓒ$-\frac{a^2+1}{a}$ ⓓ$-\frac{2a^2+1}{2a}$
ⓔ$\frac{\sqrt{a^2+4}}{2}$ ⓕ$\sqrt{a^2+1}$ ⓖ$\sqrt{4a^2+1}$ ⓗ$2a$
ⓘ$\frac{\sqrt{4a^2+1}}{2a}$ ⓙ$\frac{\sqrt{a^2+4}}{a}$ ⓚ$\frac{\sqrt{a^2+1}}{a}$ ⓛ$\frac{\sqrt{a^2+1}}{2a}$
ⓜ$\sqrt{\frac{2a^2+1}{2a}}$ ⓝ$\sqrt{\frac{4a^2+1}{2a}}$ ⓞ$\sqrt{\frac{2a^2+1}{a}}$ ⓟ$\sqrt{\frac{4a^2+1}{a}}$
$\boxed{\ \ カ\ \ }$の解答群
$ⓐ\frac{(2a^2+1)^3(a^2+1)^{\frac{3}{2}}}{60a^4}\ \pi ⓑ\frac{(2a^2+1)^{\frac{9}{2}}}{120a^4}\ \pi ⓒ\frac{(2a^2+1)^{\frac{9}{2}}}{60a^4}\ \pi$
$ⓓ\frac{(2a^2+1)^3(4a^2+1)^{\frac{3}{2}}}{60a^4}\ \pi ⓔ\frac{(4a^2+1)^{\frac{9}{2}}}{480a^4}\ \pi ⓕ\frac{(4a^2+1)^{\frac{9}{2}}}{60a^4}\ \pi$
$ⓖ\frac{(a^2+1)^2(4a^2+1)^2}{120a^{\frac{7}{2}}}\ \pi ⓗ\frac{(4a^2+1)^4}{480\sqrt2a^{\frac{7}{2}}}\ \pi ⓘ\frac{(4a^2+1)^4}{120\sqrt2a^{\frac{7}{2}}}\ \pi$
$\boxed{\ \ キ\ \ }$の解答群
$ⓐ\frac{1}{\sqrt5} ⓑ\frac{1}{\sqrt2} ⓒ1 ⓓ\sqrt2 ⓔ\frac{2}{\sqrt5} ⓕ4$
2021中央大学理工学部過去問
福田の数学〜慶應義塾大学2021年看護医療学部第5問〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$dを実数の定数、$f(t)$を2次関数として、次の関数F(x)を考える。
$F(x)=\int_d^xf(t)dt$
(1)$F(d)=\boxed{\ \ ヤ\ \ },\ F'(x)=\boxed{\ \ ユ\ \ }$である。
(2)$F(x)$が$x=1$で極大値5、$x=2$で極小値4をとるとき、
$f(t)$およびdを求めなさい。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{5}}$dを実数の定数、$f(t)$を2次関数として、次の関数F(x)を考える。
$F(x)=\int_d^xf(t)dt$
(1)$F(d)=\boxed{\ \ ヤ\ \ },\ F'(x)=\boxed{\ \ ユ\ \ }$である。
(2)$F(x)$が$x=1$で極大値5、$x=2$で極小値4をとるとき、
$f(t)$およびdを求めなさい。
2021慶應義塾大学看護医療学部過去問
積分基礎 西南学院大

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=-x^2+1$と$g(n)=-x^2+6x-5$と$f(x),g(n)$の共通接線で囲まれる面積を求めよ.
2021西南学院大過去問
この動画を見る
$f(x)=-x^2+1$と$g(n)=-x^2+6x-5$と$f(x),g(n)$の共通接線で囲まれる面積を求めよ.
2021西南学院大過去問
高専数学 微積II #64 偏微分の計算
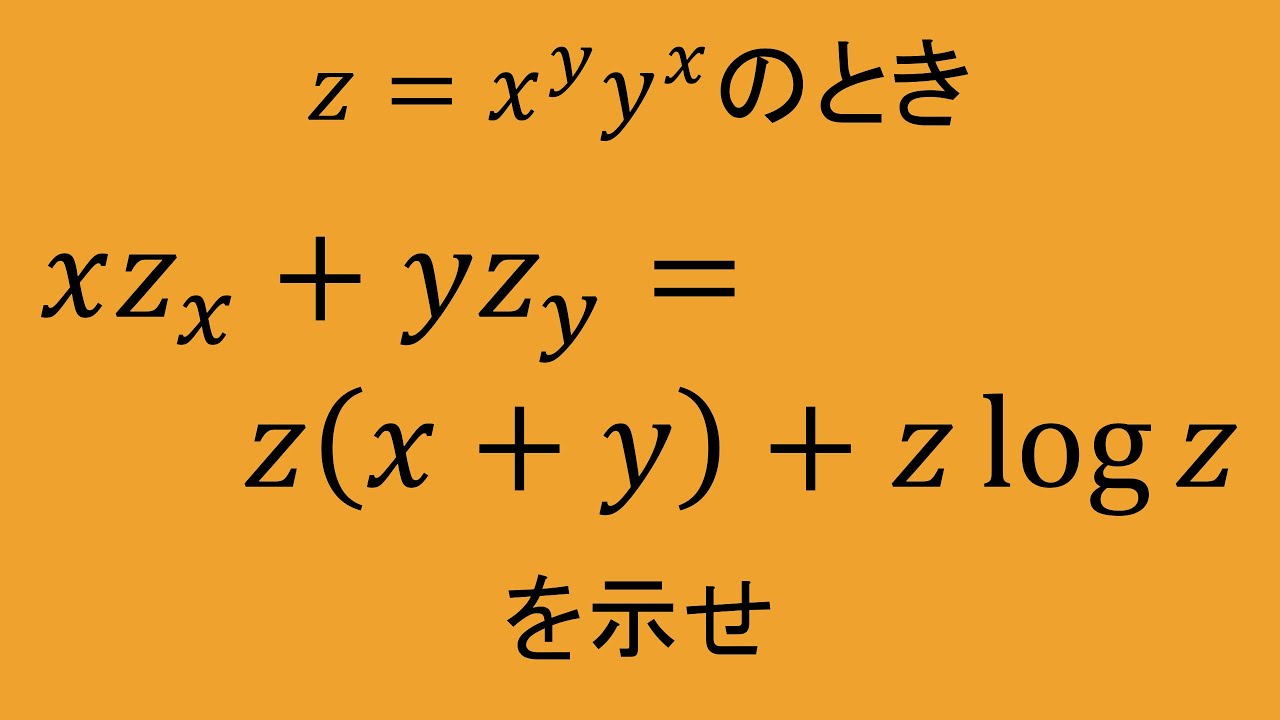
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$z=x^y y^x$のとき,
$xz_x+yz_y=z(x+y)+z\log z$が
成り立つことを示せ.
この動画を見る
$z=x^y y^x$のとき,
$xz_x+yz_y=z(x+y)+z\log z$が
成り立つことを示せ.
高専数学 微積II #61(1)(2) 合成関数の微分法
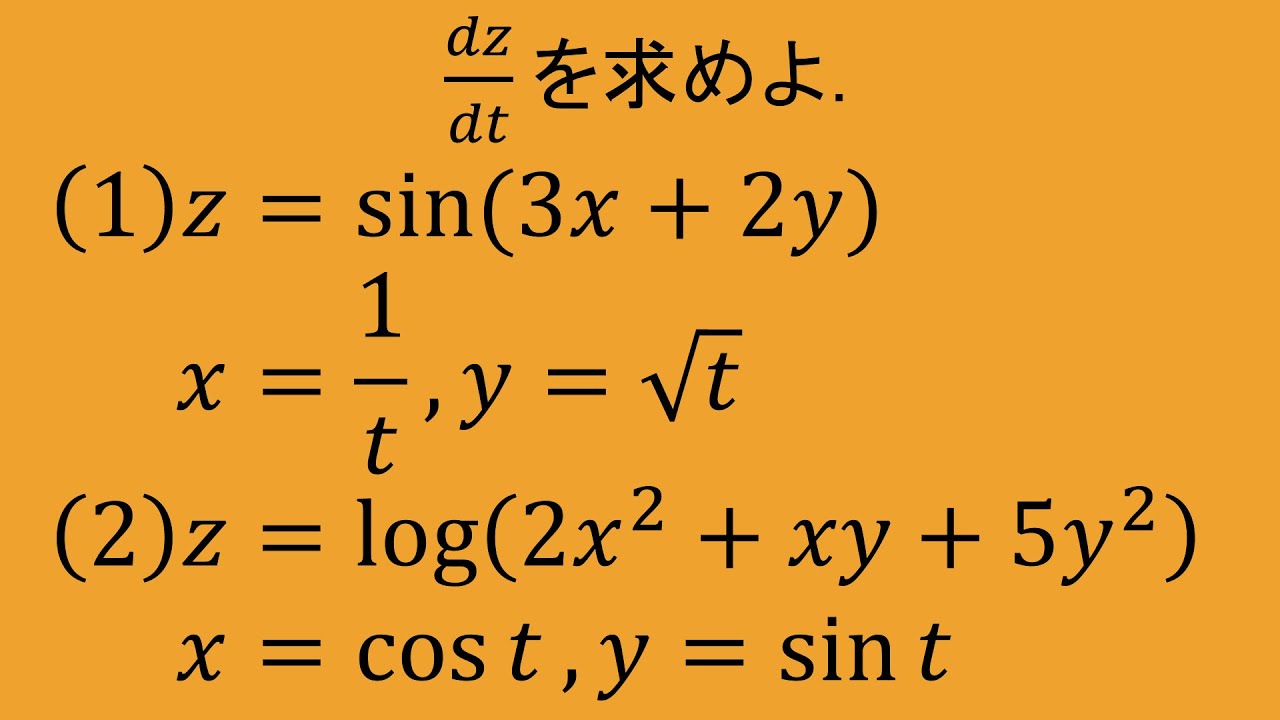
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\dfrac{dz}{dt}$を求めよ.
(1)$z=\sin (3x+2y)$
$x=\dfrac{1}{t},y=\sqrt t$
(2)$z=\log(2x^2+xy+5y^2)$
$x=\cos t,y=\sin t$
この動画を見る
$\dfrac{dz}{dt}$を求めよ.
(1)$z=\sin (3x+2y)$
$x=\dfrac{1}{t},y=\sqrt t$
(2)$z=\log(2x^2+xy+5y^2)$
$x=\cos t,y=\sin t$
【基本から解説】数Ⅲ・微分 導関数の定義に従って微分する問題

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の関数を、導関数の定義に従って微分せよ。
(1)
$y=\displaystyle \frac{1}{x+2}$
(2)
$y=\sqrt{ 3x }$
この動画を見る
次の関数を、導関数の定義に従って微分せよ。
(1)
$y=\displaystyle \frac{1}{x+2}$
(2)
$y=\sqrt{ 3x }$
高専数学 微積II #53(3)(4) 合成関数の微分法

単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を,$u,\nu,z_x,z_y$で表せ.
(3)$x=\tan\dfrac{\nu}{u},y-\cos(u+\nu)$
(4)$x=u\log\nu,y=e^u \nu$
この動画を見る
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を,$u,\nu,z_x,z_y$で表せ.
(3)$x=\tan\dfrac{\nu}{u},y-\cos(u+\nu)$
(4)$x=u\log\nu,y=e^u \nu$
高専数学 微積II #53(1)(2) 合成関数の微分法
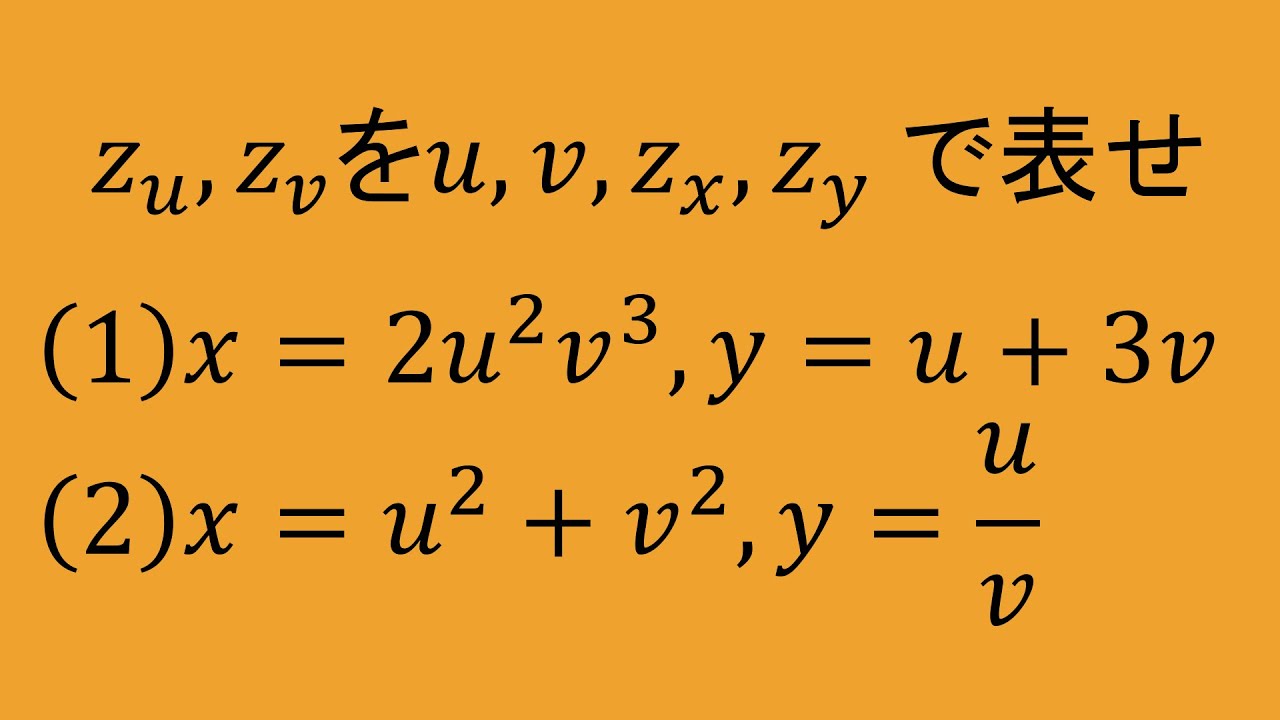
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を$u,\nu,z_x,z_y$で表せ.
(1)$x=2u^2 \nu^3,y=u+3\nu$
(2)$x=u^2+\nu^2,y=\dfrac{u}{\nu}$
この動画を見る
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を$u,\nu,z_x,z_y$で表せ.
(1)$x=2u^2 \nu^3,y=u+3\nu$
(2)$x=u^2+\nu^2,y=\dfrac{u}{\nu}$
11三重県教員採用試験(数学:5-(2) 極限値)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}(2)$
$\displaystyle \lim_{x\to\infty} (2-3x)\sin \left\{\log(2x+2)-\log(2x+1)\right\}$の
極限値を求めよ.
この動画を見る
$\boxed{5}(2)$
$\displaystyle \lim_{x\to\infty} (2-3x)\sin \left\{\log(2x+2)-\log(2x+1)\right\}$の
極限値を求めよ.
高専数学 微積II #51(3)(4) 合成関数の微分法
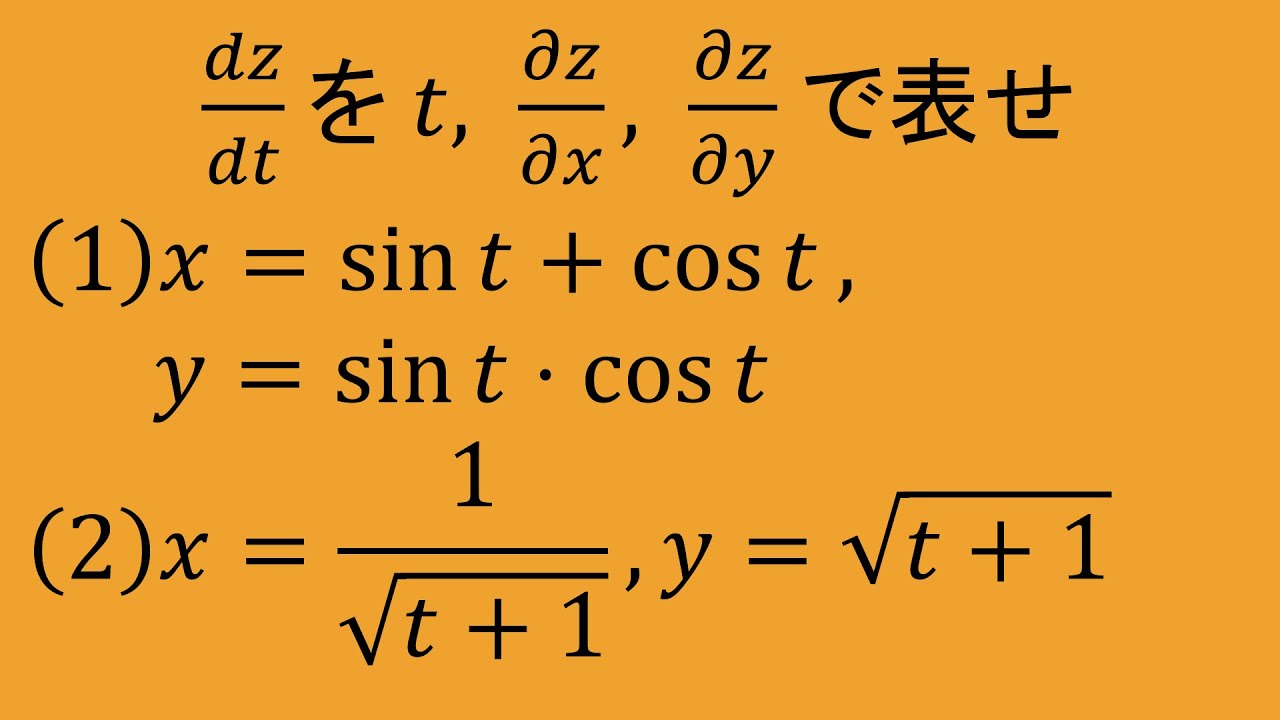
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$\dfrac{dz}{dt}$を$t,\dfrac{\alpha z}{\alpha x},\dfrac{\alpha z}{\alpha y}$で表せ.
(3)$x=\sin t+\cos t$
$y=\sin t \cos t$
(4)$x=\dfrac{1}{\sqrt{x+1}}$
$y=\sqrt{t+1}$
この動画を見る
$z=f(x,y)$:全微分可能
$\dfrac{dz}{dt}$を$t,\dfrac{\alpha z}{\alpha x},\dfrac{\alpha z}{\alpha y}$で表せ.
(3)$x=\sin t+\cos t$
$y=\sin t \cos t$
(4)$x=\dfrac{1}{\sqrt{x+1}}$
$y=\sqrt{t+1}$
07三重県教員採用試験(数学:11番 積分)
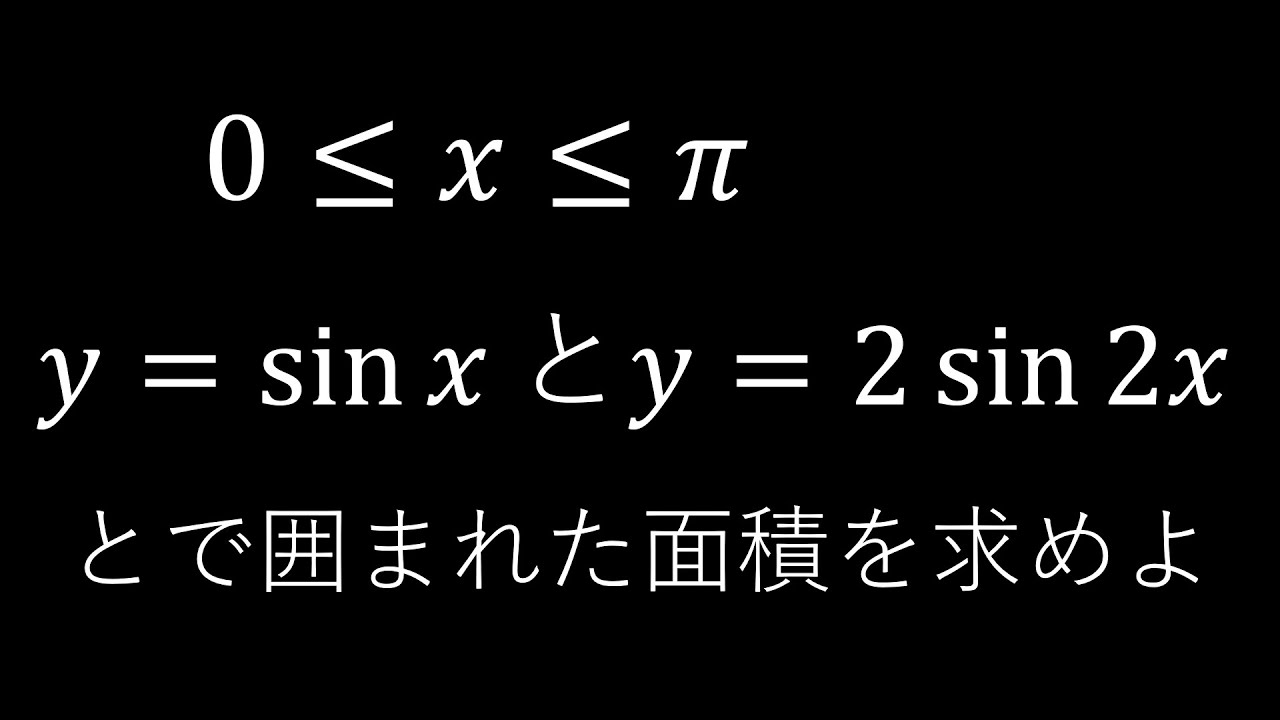
単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{11}$
$0\leqq x\leqq \pi$である.
$y=\sin x$と$y=2\sin 2x$とで囲まれた図形の
面積を求めよ.
この動画を見る
$\boxed{11}$
$0\leqq x\leqq \pi$である.
$y=\sin x$と$y=2\sin 2x$とで囲まれた図形の
面積を求めよ.
高専数学 微積II #51(1)(2) 合成関数の微分法

単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
この動画を見る
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
高専数学 微積II #50(3)(4) 曲面の接平面の方程式

単元:
#数Ⅱ#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の曲面上の点における接平面の方程式を求めよ.
(3)$z=\sin(x^-2-y^2)$
$x=1,y=1$
(4)$z=\log(x^2+y^2)$
$x=1,y=0$
この動画を見る
次の曲面上の点における接平面の方程式を求めよ.
(3)$z=\sin(x^-2-y^2)$
$x=1,y=1$
(4)$z=\log(x^2+y^2)$
$x=1,y=0$
福田の数学〜慶應義塾大学2021年薬学部第3問〜3次関数と接線

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$xy平面上に、xの関数
$f(x)=x^3+(a+4)x^2+(4a+6)x+4a+2$
のグラフ$y=f(x)$がある。$y=f(x)$が任意のaに対して
通る定点をP、点Pにおける接線が$y=f(x)$と交わる点をQとおく。
(1)点Pの座標は$\boxed{\ \ ツ\ \ }$であり、点Pにおける接線の方程式は$y=\boxed{\ \ テ\ \ }$である。
(2)$a=5$のとき、$y=f(x)$上の点における接線は、$x=\boxed{\ \ ト\ \ }$において傾きが
最小になる。
(3)$x=\boxed{\ \ ト\ \ }$において$f(x)$が極値をとるとき、$a=\boxed{\ \ ナ\ \ }$であり、
点$(\boxed{\ \ ト\ \ },f(\boxed{\ \ ト\ \ }))$を$S$とおくと、三角形SPQの面積は$\boxed{\ \ ニ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{3}}$xy平面上に、xの関数
$f(x)=x^3+(a+4)x^2+(4a+6)x+4a+2$
のグラフ$y=f(x)$がある。$y=f(x)$が任意のaに対して
通る定点をP、点Pにおける接線が$y=f(x)$と交わる点をQとおく。
(1)点Pの座標は$\boxed{\ \ ツ\ \ }$であり、点Pにおける接線の方程式は$y=\boxed{\ \ テ\ \ }$である。
(2)$a=5$のとき、$y=f(x)$上の点における接線は、$x=\boxed{\ \ ト\ \ }$において傾きが
最小になる。
(3)$x=\boxed{\ \ ト\ \ }$において$f(x)$が極値をとるとき、$a=\boxed{\ \ ナ\ \ }$であり、
点$(\boxed{\ \ ト\ \ },f(\boxed{\ \ ト\ \ }))$を$S$とおくと、三角形SPQの面積は$\boxed{\ \ ニ\ \ }$である。
2021慶應義塾大学薬学部過去問
高専数学 微積II #50(1)(2) 曲面の接平面の方程式

単元:
#数Ⅱ#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の曲面上の点における接平面の方程式を求めよ.
(1)$z=x^2+2y^2 \ (1,1,3)$
(2)$z=\sqrt{5-x^2y^2} \ (1,2,1)$
この動画を見る
次の曲面上の点における接平面の方程式を求めよ.
(1)$z=x^2+2y^2 \ (1,1,3)$
(2)$z=\sqrt{5-x^2y^2} \ (1,2,1)$
09高知県教員採用試験(数学:1-(4) 不定形の極限)
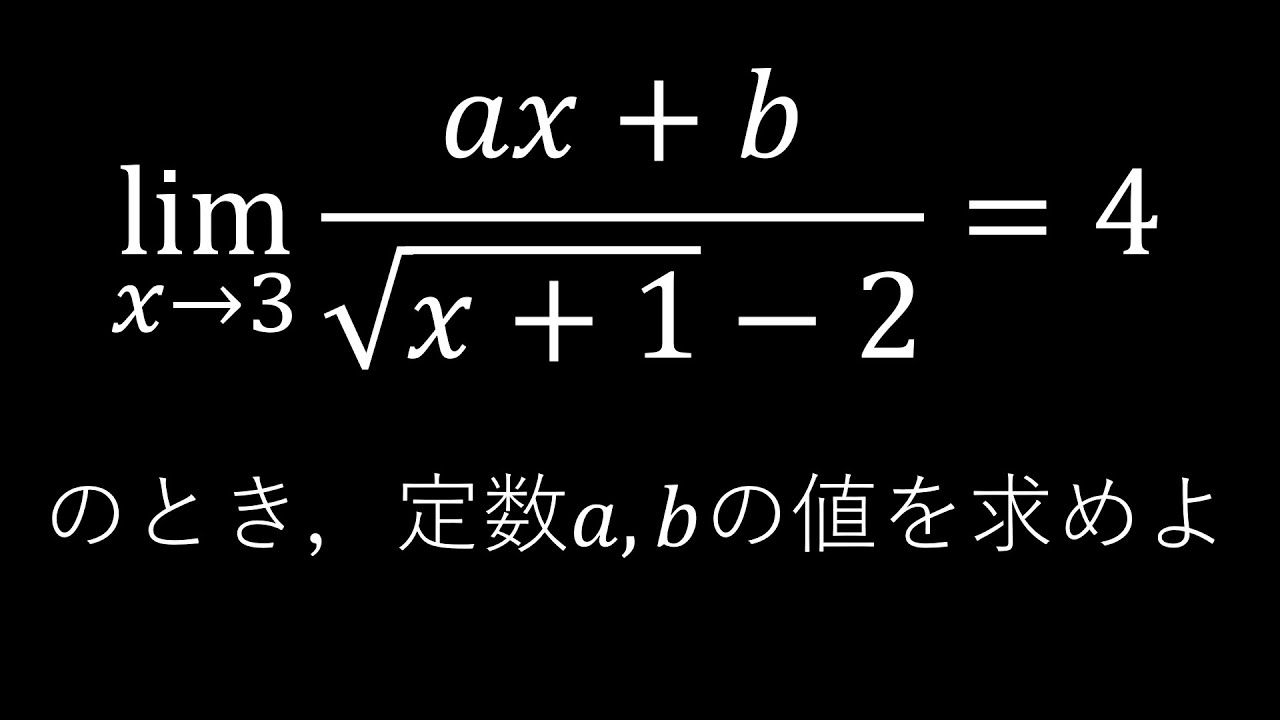
単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(4)$
$\displaystyle \lim_{x\to 3}\dfrac{ax+b}{\sqrt{x+1}-2}=4$のとき,
定数$a,b$の値を求めよ.
この動画を見る
$\boxed{1}-(4)$
$\displaystyle \lim_{x\to 3}\dfrac{ax+b}{\sqrt{x+1}-2}=4$のとき,
定数$a,b$の値を求めよ.
高専数学 微積II #48(4)(5) 全微分
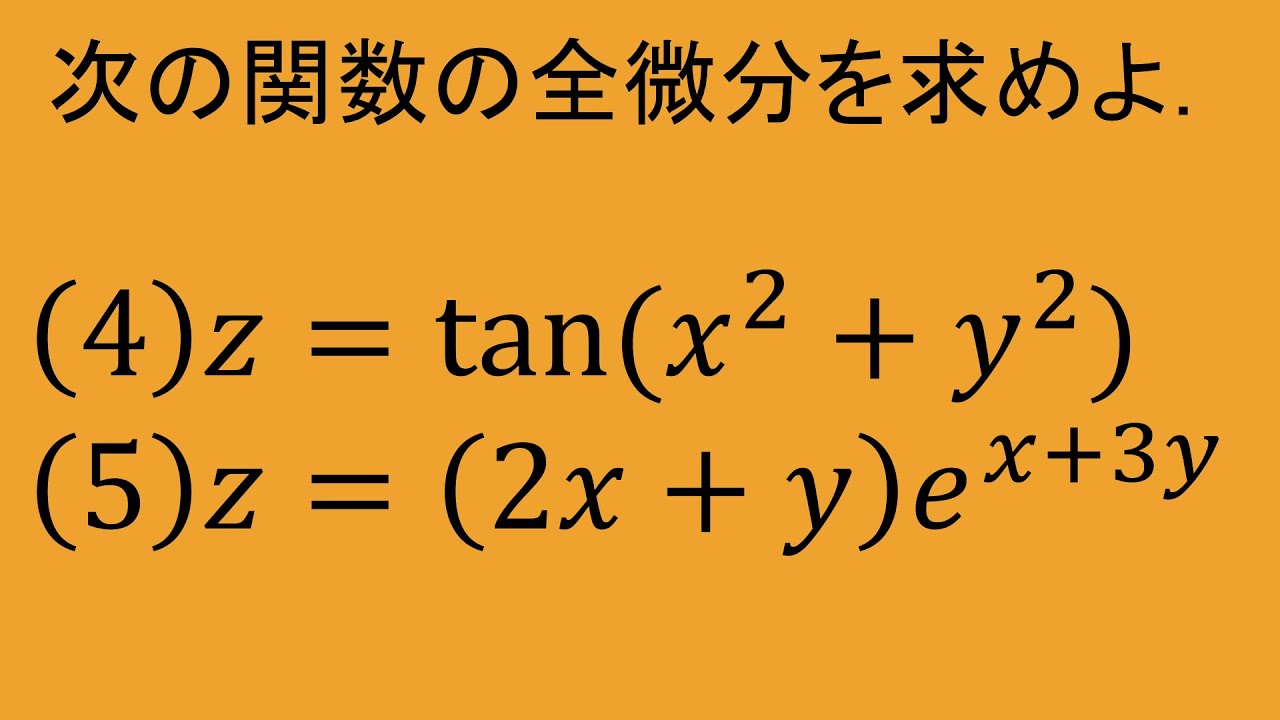
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の関数$z=f(x,y)$の全微分$dz$を求めよ.
(4)$z=\tan(x^2+y^2)$
(5)$z=(2x+y)e^{x+3y}$
この動画を見る
次の関数$z=f(x,y)$の全微分$dz$を求めよ.
(4)$z=\tan(x^2+y^2)$
(5)$z=(2x+y)e^{x+3y}$
高専数学 微積II #43(1)(2) 平面の法線ベクトル
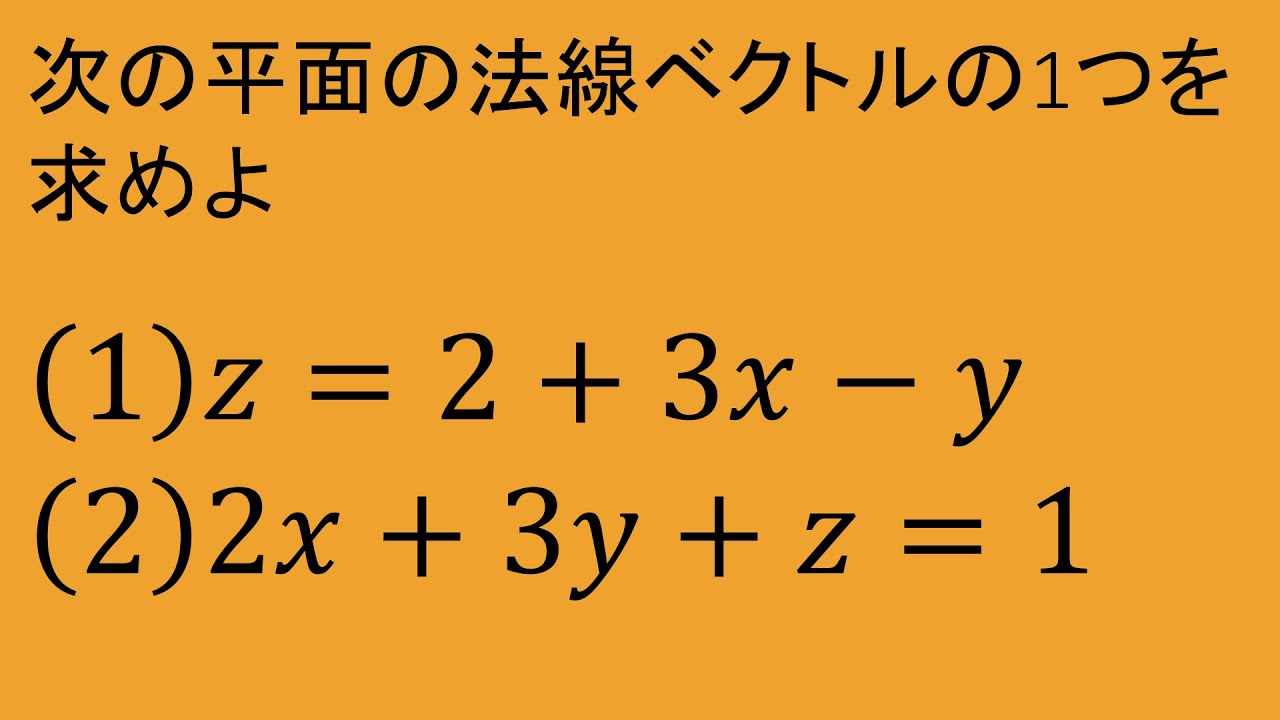
単元:
#数Ⅱ#平面上のベクトル#微分法と積分法#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
次の平面の法線ベクトルの1つを求めよ.
(1)$z=2+3x-y$
(2)$2x+3y+z=1$
この動画を見る
次の平面の法線ベクトルの1つを求めよ.
(1)$z=2+3x-y$
(2)$2x+3y+z=1$
練習問題39 数研1級1次 教採対応 定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\dfrac{x+3}{x^2-2x+2}dx$
を計算せよ.
この動画を見る
$\displaystyle \int_{0}^{1}\dfrac{x+3}{x^2-2x+2}dx$
を計算せよ.
