 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
高専数学 微積II #2(3)(4) 2次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x=0$における2次近似式を求め等式で表せ.
(1)$\cos 2x$
(2)$\log (1+2x)$
この動画を見る
$x=0$における2次近似式を求め等式で表せ.
(1)$\cos 2x$
(2)$\log (1+2x)$
高専数学 微積II #2(1)(2) 2次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x=0$における2次近似式を求め等式で表せ.
(1)$e^{3x}$
(2)$x\sqrt{1+x}$
この動画を見る
$x=0$における2次近似式を求め等式で表せ.
(1)$e^{3x}$
(2)$x\sqrt{1+x}$
高専数学 微積II n次近似式
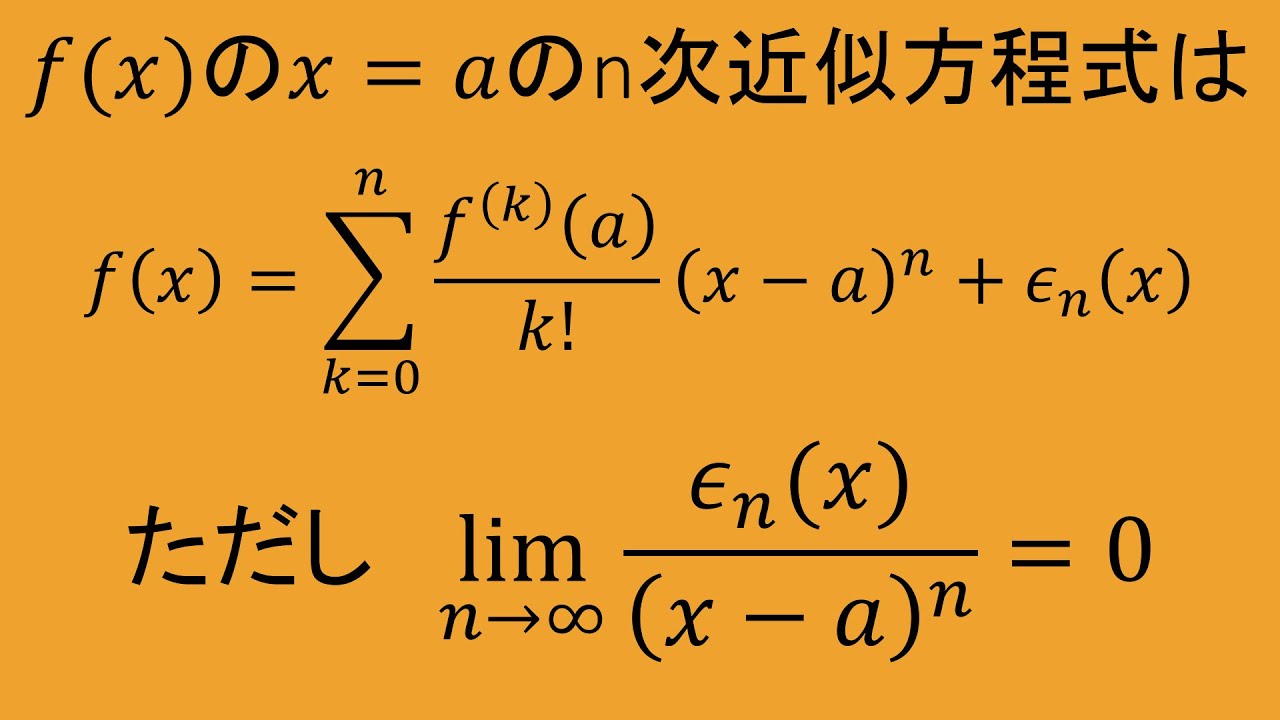
単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
この動画を見る
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
高専数学 微積II #1(1)(2) 1次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)$の$x=a$における一次近似式は
$f(a)+f`(a)(x-a)$
次の点における一次近似式を求めよ.
(1)$e^{2x}\cos x \ (x=0)$
(2)$\dfrac{1}{x} \ (x=1)$
この動画を見る
$f(x)$の$x=a$における一次近似式は
$f(a)+f`(a)(x-a)$
次の点における一次近似式を求めよ.
(1)$e^{2x}\cos x \ (x=0)$
(2)$\dfrac{1}{x} \ (x=1)$
言語学オタクに数学を教えるよ!その2 ネイピア数とは

高専数学 微積I 254 広義積分
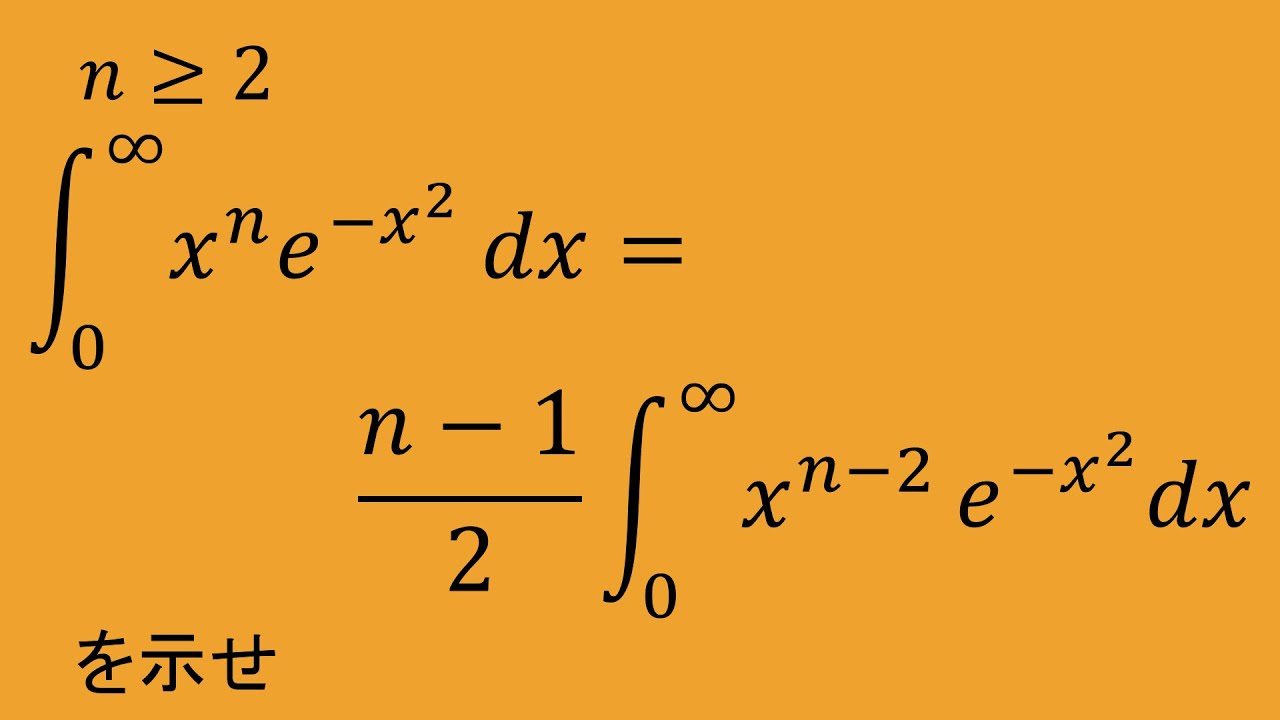
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n\geqq 2$である.
$\displaystyle \int_{0}^{\infty} x^n e^{-x^2} dx=\dfrac{n-1}{2} \displaystyle \int_{0}^{\infty} x^{n-2} e^{-x^2} dx$
が成り立つことを示せ.
この動画を見る
$n\geqq 2$である.
$\displaystyle \int_{0}^{\infty} x^n e^{-x^2} dx=\dfrac{n-1}{2} \displaystyle \int_{0}^{\infty} x^{n-2} e^{-x^2} dx$
が成り立つことを示せ.
ゆる言語学者に数学を教えるよ!その1sinの微分

高専数学 微積I #258 媒介変数表示曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
この動画を見る
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
高専数学 微積I p 62ex(2) 広義積分
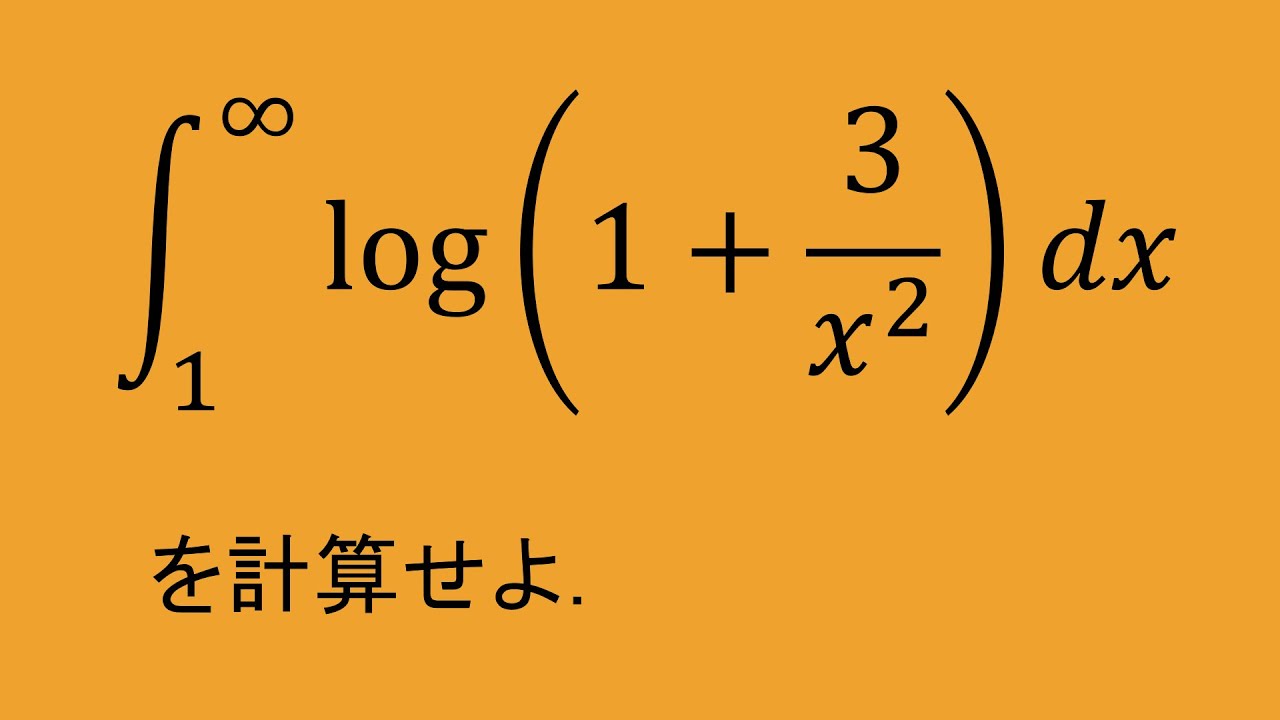
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\infty}\log \left(1+\dfrac{3}{x^2}\right)dx$
を計算せよ.
この動画を見る
$\displaystyle \int_{1}^{\infty}\log \left(1+\dfrac{3}{x^2}\right)dx$
を計算せよ.
練習問題36 (数検1級1次 教採 極限値)
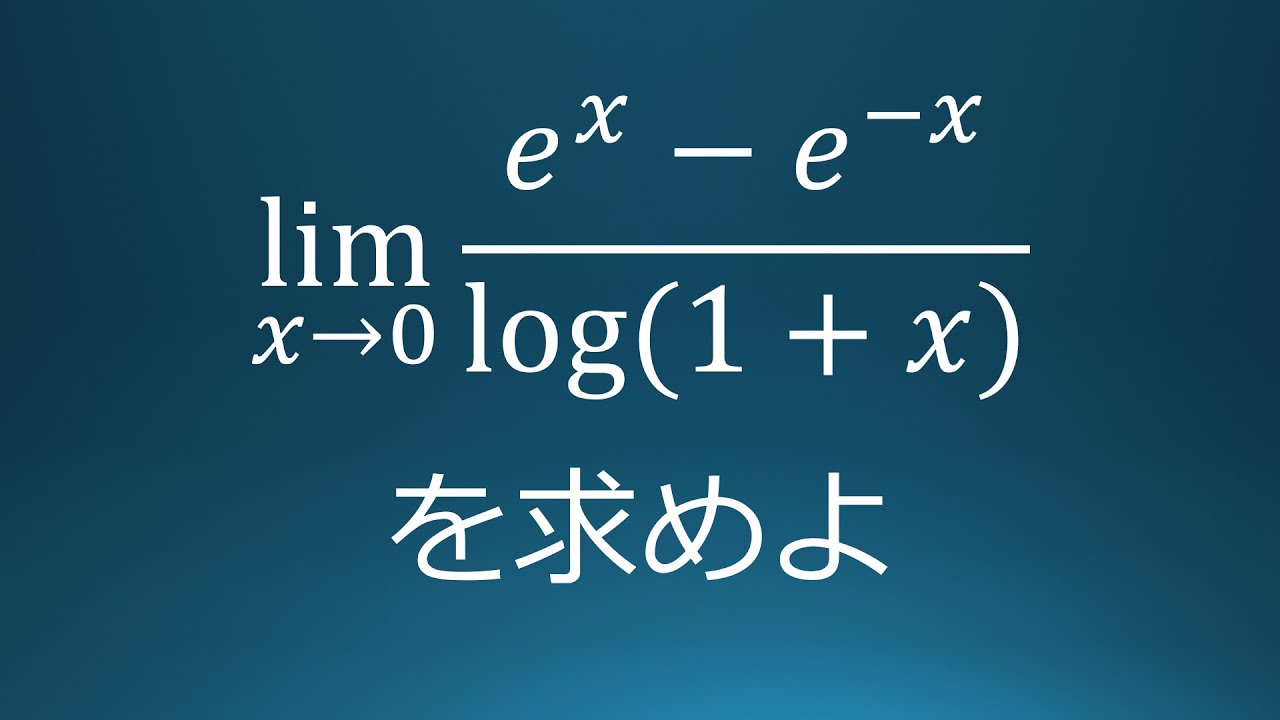
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} \dfrac{e^x-e^{-x}}{\log (1+x)}$
を求めよ.
この動画を見る
$\displaystyle \lim_{x\to\infty} \dfrac{e^x-e^{-x}}{\log (1+x)}$
を求めよ.
高専数学 微積I #259(2) 広義積分
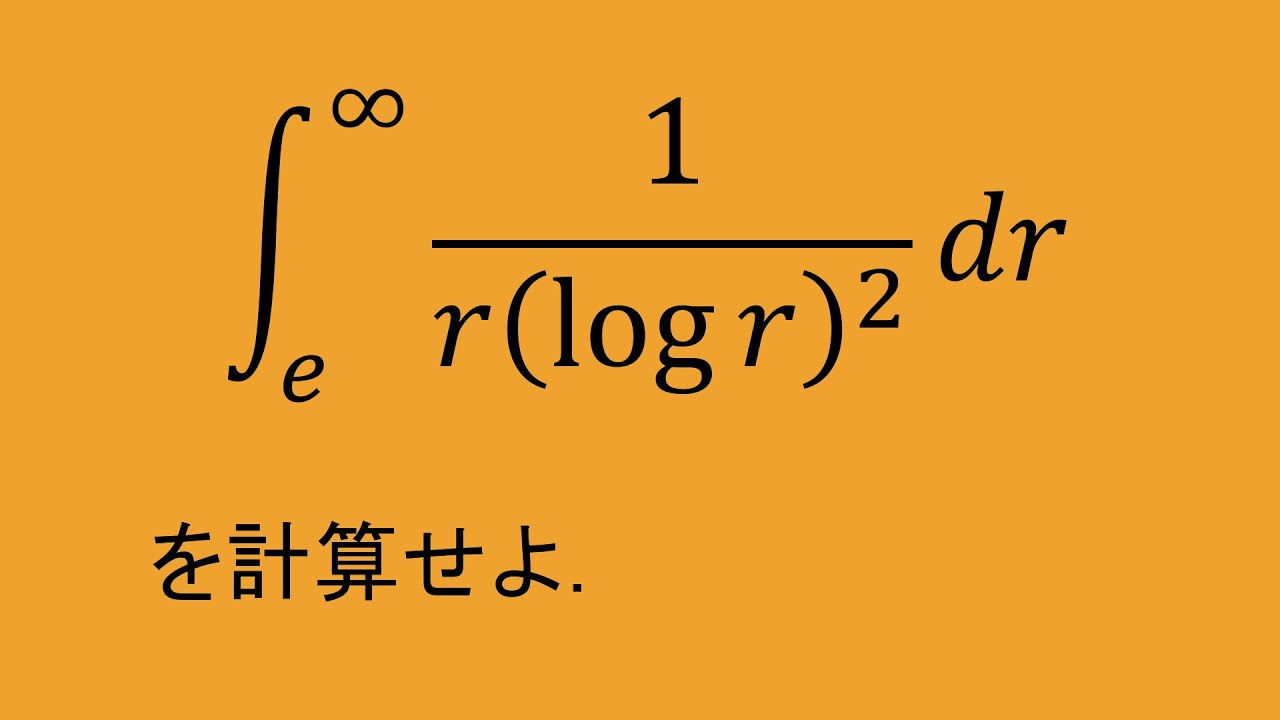
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{\infty}\dfrac{1}{r(\log r)^2} dr$
を計算せよ.
この動画を見る
$\displaystyle \int_{e}^{\infty}\dfrac{1}{r(\log r)^2} dr$
を計算せよ.
高専数学 微積I #259(1) 広義積分
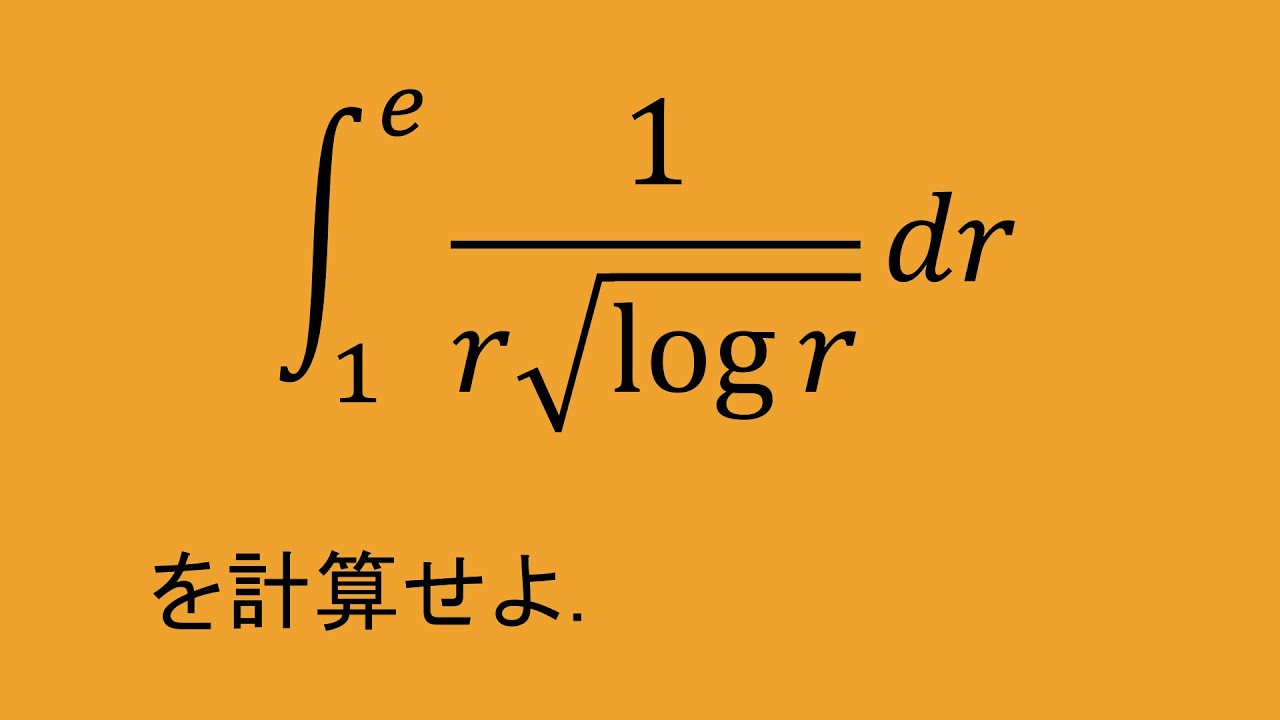
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\dfrac{1}{r\sqrt{\log r}} dr$を計算せよ.
この動画を見る
$\displaystyle \int_{1}^{e}\dfrac{1}{r\sqrt{\log r}} dr$を計算せよ.
09兵庫県教員採用試験(数学:5番 面積)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
曲線$y=\vert x \vert \sqrt{2x+1}$
と$x$軸で囲まれた部分の面積を求めよ.
この動画を見る
$\boxed{5}$
曲線$y=\vert x \vert \sqrt{2x+1}$
と$x$軸で囲まれた部分の面積を求めよ.
高専数学 微積I #p 62 ex(1)
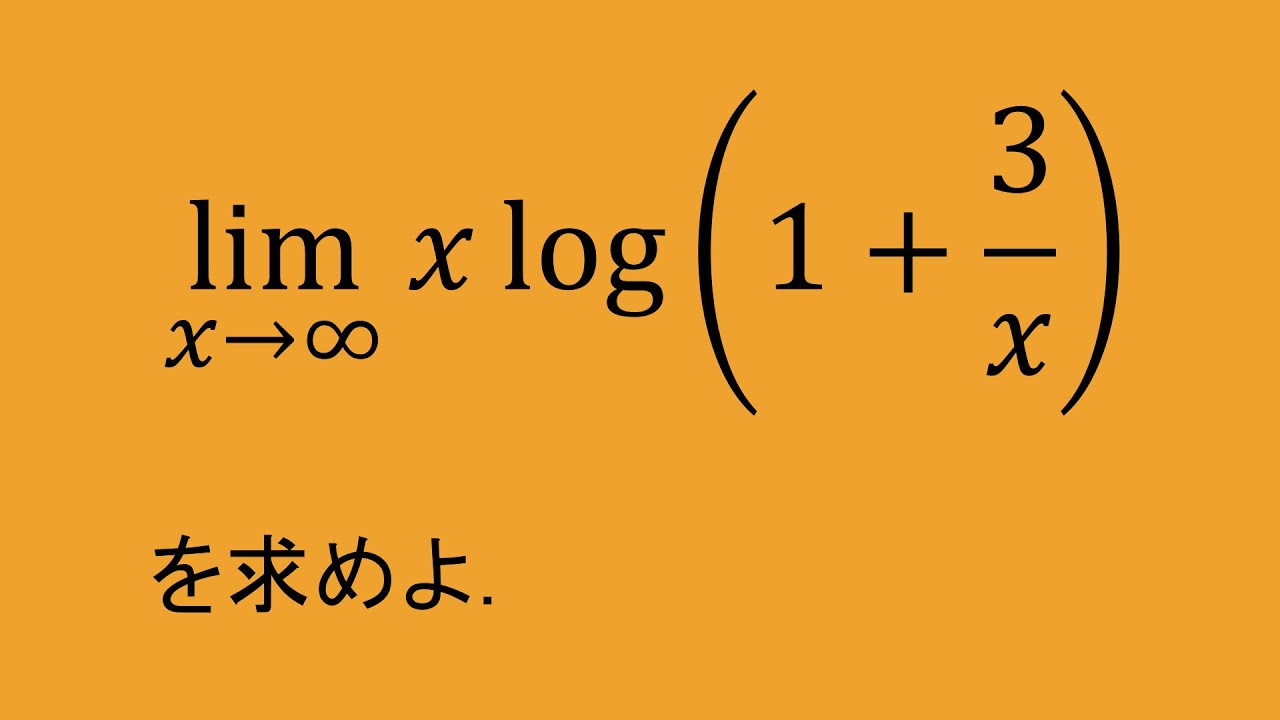
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty}x \log \left(1+\dfrac{3}{x}\right)$
を求めよ.
この動画を見る
$\displaystyle \lim_{x\to\infty}x \log \left(1+\dfrac{3}{x}\right)$
を求めよ.
高専数学 微積I #248(2) 極座標表示曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq \theta \leqq 4\pi$である.
極座標による曲線$r=\sin^4\dfrac{\theta}{4}$
の長さを求めよ.
この動画を見る
$0\leqq \theta \leqq 4\pi$である.
極座標による曲線$r=\sin^4\dfrac{\theta}{4}$
の長さを求めよ.
高専数学 微積I #243(2) 媒介変数表示関数のx軸回転体

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq t \leqq 1$である.
曲線$x=t^2,y=e^t$
$x$軸,$y$軸,直線$x=1$で囲まれた図形を
$x$軸を中心とした回転体の体積$V$を求めよ.
この動画を見る
$0 \leqq t \leqq 1$である.
曲線$x=t^2,y=e^t$
$x$軸,$y$軸,直線$x=1$で囲まれた図形を
$x$軸を中心とした回転体の体積$V$を求めよ.
21滋賀県教員採用試験(数学:5番 接線の本数)

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$a$は実数である.
点$(a,0)$を通る曲線
$y=(2-x)e^x$の接線の本数を求めよ.
この動画を見る
$\boxed{5}$
$a$は実数である.
点$(a,0)$を通る曲線
$y=(2-x)e^x$の接線の本数を求めよ.
高専数学 微積I #243(1) 媒介変数曲線(x軸回転体)

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
この動画を見る
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
高専数学 微積I #242(2) 媒介変数表示曲線の長さ
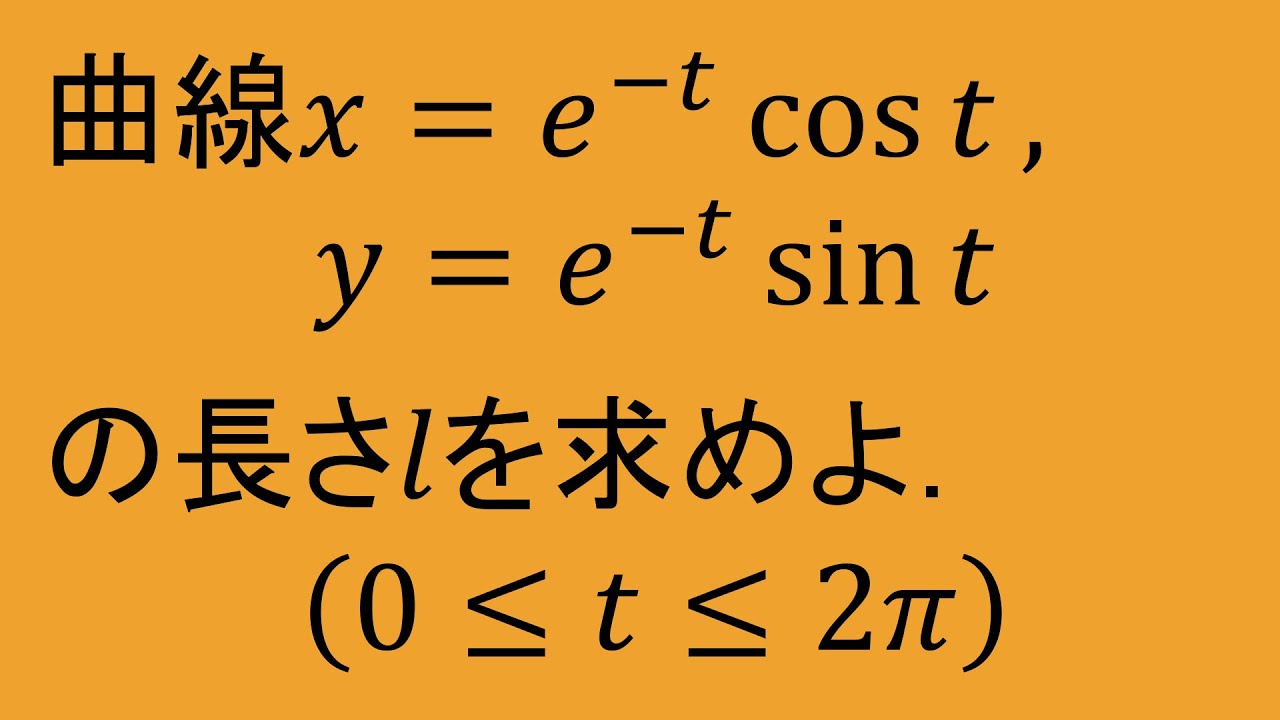
単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
この動画を見る
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
高専数学 微積I #242(1) 媒介変数表示曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
この動画を見る
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
高専数学 微積I #238(3)(4) 広義積分

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{\sqrt[3]{x^2}}$
(4)$\displaystyle \int_{0}^{\infty}x \ e^{-x} dx$
この動画を見る
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{\sqrt[3]{x^2}}$
(4)$\displaystyle \int_{0}^{\infty}x \ e^{-x} dx$
高専数学 微積I #238(1)(2) 広義積分

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{\infty}x^{-5} dx$
(2)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{e^{2x}}$
この動画を見る
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{\infty}x^{-5} dx$
(2)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{e^{2x}}$
高専数学 微積I #236(3)(4) 広義積分

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{1}\dfrac{dx}{\sqrt[4]{x}}$
(4)$\displaystyle \int_{-1}^{1}\dfrac{dx}{x^4}$
この動画を見る
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{1}\dfrac{dx}{\sqrt[4]{x}}$
(4)$\displaystyle \int_{-1}^{1}\dfrac{dx}{x^4}$
高専数学 微積I #236(1)(2) 広義積分

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{3}\dfrac{dx}{\sqrt{x-2}}$
(2)$\displaystyle \int_{0}^{3}\dfrac{dx}{\sqrt{9-x^2}}$
この動画を見る
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{3}\dfrac{dx}{\sqrt{x-2}}$
(2)$\displaystyle \int_{0}^{3}\dfrac{dx}{\sqrt{9-x^2}}$
12和歌山県教員採用試験(数学:1-(5) 相加・相乗平均)
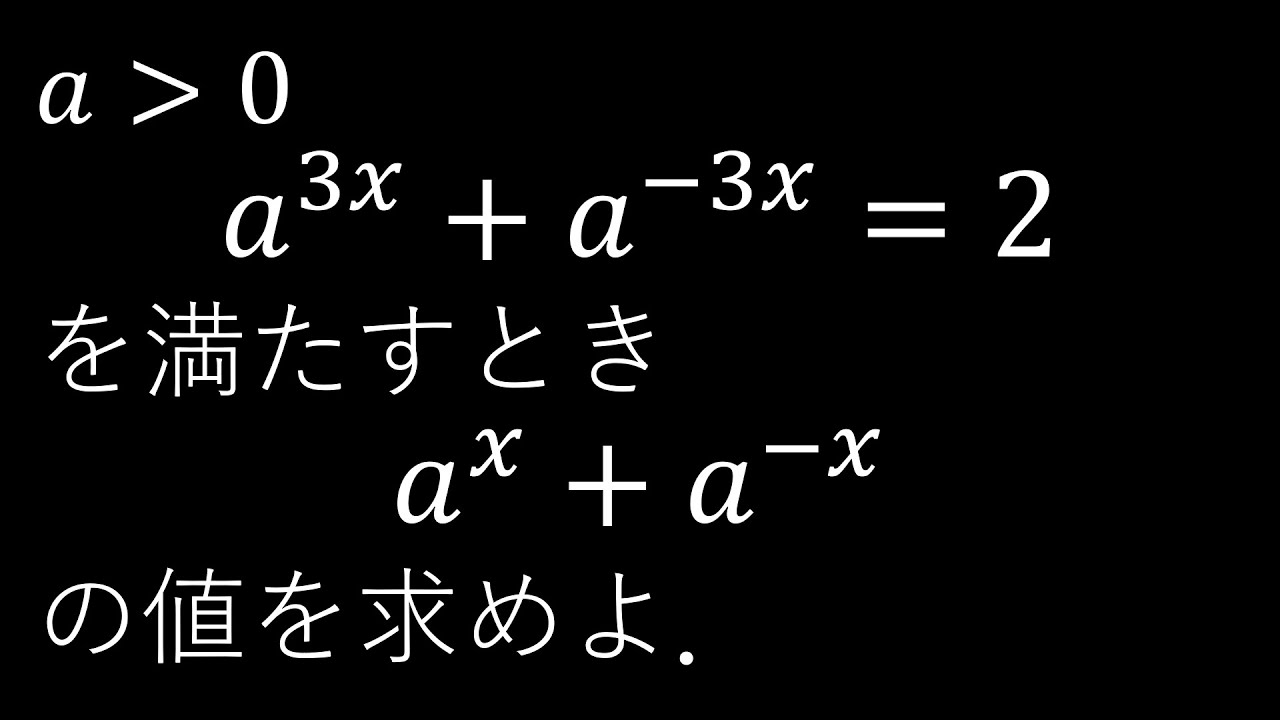
単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(5)$
$a\gt 0$とする.
$a^{3x}+a^{-3x}=2$のとき,
$a^x+a^{-x}$の値を求めよ.
この動画を見る
$\boxed{1}-(5)$
$a\gt 0$とする.
$a^{3x}+a^{-3x}=2$のとき,
$a^x+a^{-x}$の値を求めよ.
高専数学 微積I #234(1)(2) 極座標表示の曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
この動画を見る
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
高専数学 微積I #229(2) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
高専数学 微積I #229(1) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
高専数学 微積I #227(3) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
共有点の個数
単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
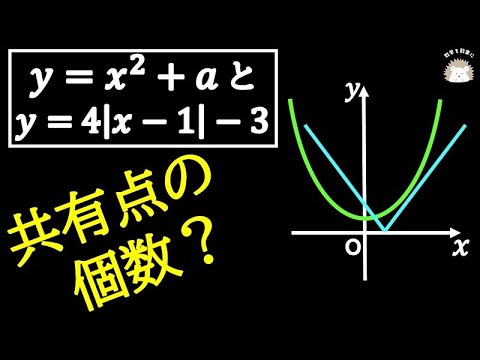
aは定数。放物線$y=x^2+a$と$y=4|x-1|-3$のグラフとの共有点の個数を求めよ。
この動画を見る
aは定数。放物線$y=x^2+a$と$y=4|x-1|-3$のグラフとの共有点の個数を求めよ。
