微分法と積分法
微分法と積分法
#京都大学1937#極限_59
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
#弘前大学2023#定積分_58
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
#弘前大学2023#定積分_57
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
京大らしさ全開の不朽の名作 京都帝国大学1937 大学入試問題#932
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
#弘前大学2024#定積分_56
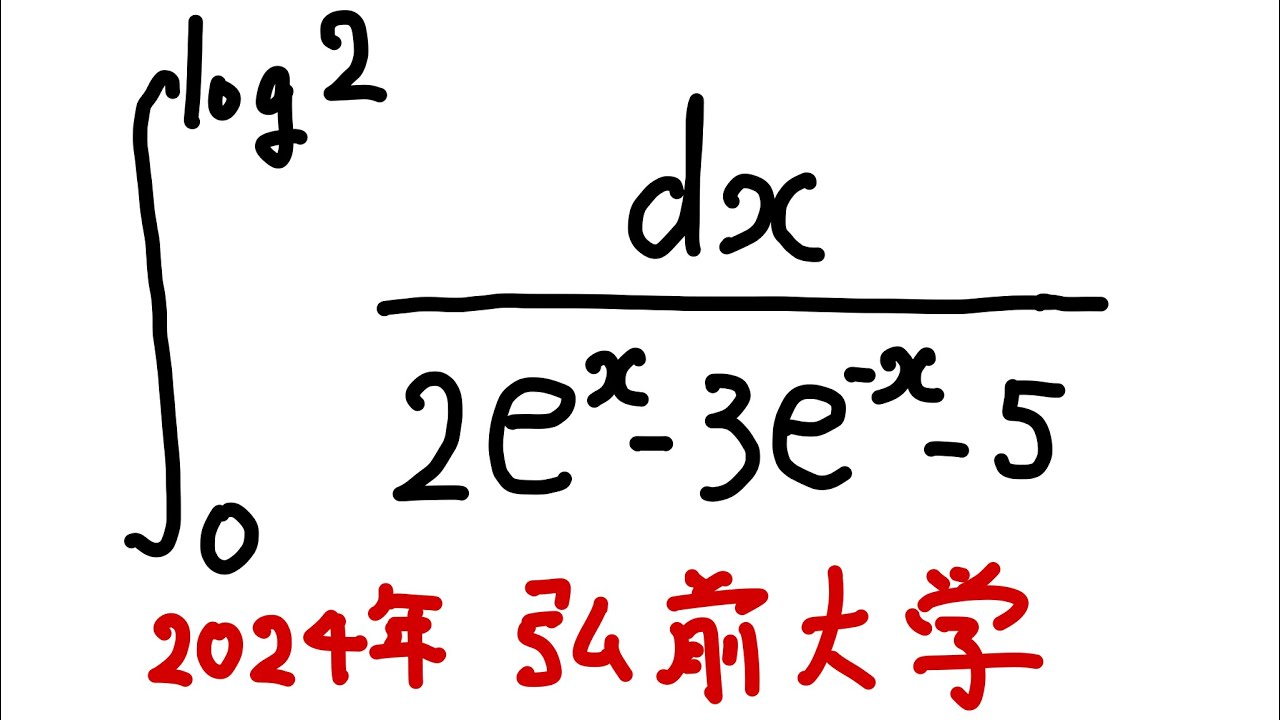
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
この動画を見る
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
#京都帝国大学1937#微分_55
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$y=e^{x^x}$なるとき,
$\dfrac{dy}{dx}$を求めよ.
1937京都帝国大学過去問題
この動画を見る
$y=e^{x^x}$なるとき,
$\dfrac{dy}{dx}$を求めよ.
1937京都帝国大学過去問題
#京都大学1937#不定積分_54
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^6}}dx$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^6}}dx$を解け.
1937京都帝国大学過去問題
#電気通信大学2024#不定積分_53
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} e^x \sqrt{6-e^x} dx$を解け.
2024電気通信大学過去問題
この動画を見る
$\displaystyle \int_{}^{} e^x \sqrt{6-e^x} dx$を解け.
2024電気通信大学過去問題
突破口を探す不定積分 京都帝国大学1936 大学入試問題#931
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$ \sec \ x=\dfrac{1}{\cos x}$とする.
$\displaystyle \int_{}^{} \sec \ x \ \tan^2 x \ dx$を解け.
1936京都帝国大学過去問題
この動画を見る
$ \sec \ x=\dfrac{1}{\cos x}$とする.
$\displaystyle \int_{}^{} \sec \ x \ \tan^2 x \ dx$を解け.
1936京都帝国大学過去問題
#京都帝国大学1935#不定積分_52
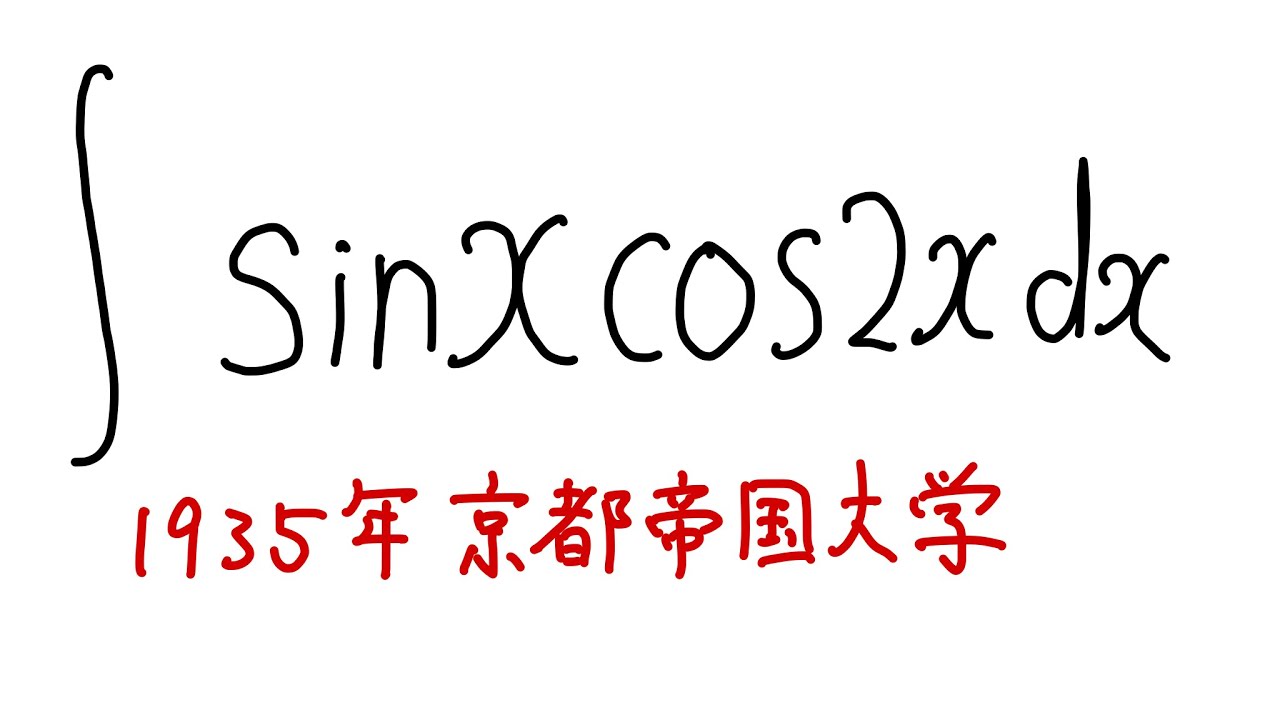
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \sin x \ \cos 2x \ dx$を解け.
1935京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \sin x \ \cos 2x \ dx$を解け.
1935京都帝国大学過去問題
#京都帝国大学1937#不定積分_51
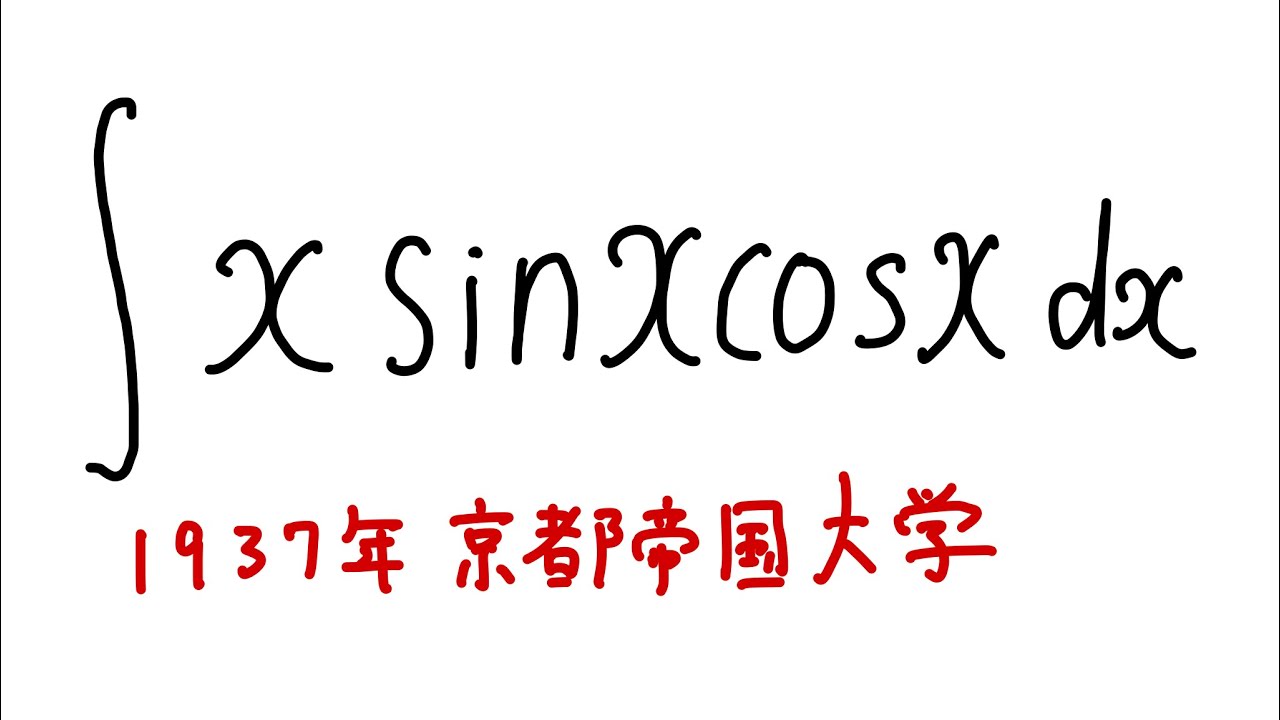
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x \ \sin x\ \cos x \ dx$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \sin x\ \cos x \ dx$を解け.
1937京都帝国大学過去問題
定積分の微分の基本問題 島根大学後期2024 大学入試問題#930
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学
指導講師：
ますただ
問題文全文(内容文)：
$a$の正の定数とする.
関数$g(x)$が,$x\gt 0$で定義された連続関数で,
次の等式をみたすとき,$g(x)$と$a$の値を求めよ.
$\displaystyle \int_{a}^{x^3} g(u) du =\log x$
2024島根大学後期過去問題
この動画を見る
$a$の正の定数とする.
関数$g(x)$が,$x\gt 0$で定義された連続関数で,
次の等式をみたすとき,$g(x)$と$a$の値を求めよ.
$\displaystyle \int_{a}^{x^3} g(u) du =\log x$
2024島根大学後期過去問題
#三重大学医学部2023#極限_50
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
#三重大学医学部2023#不定積分_49
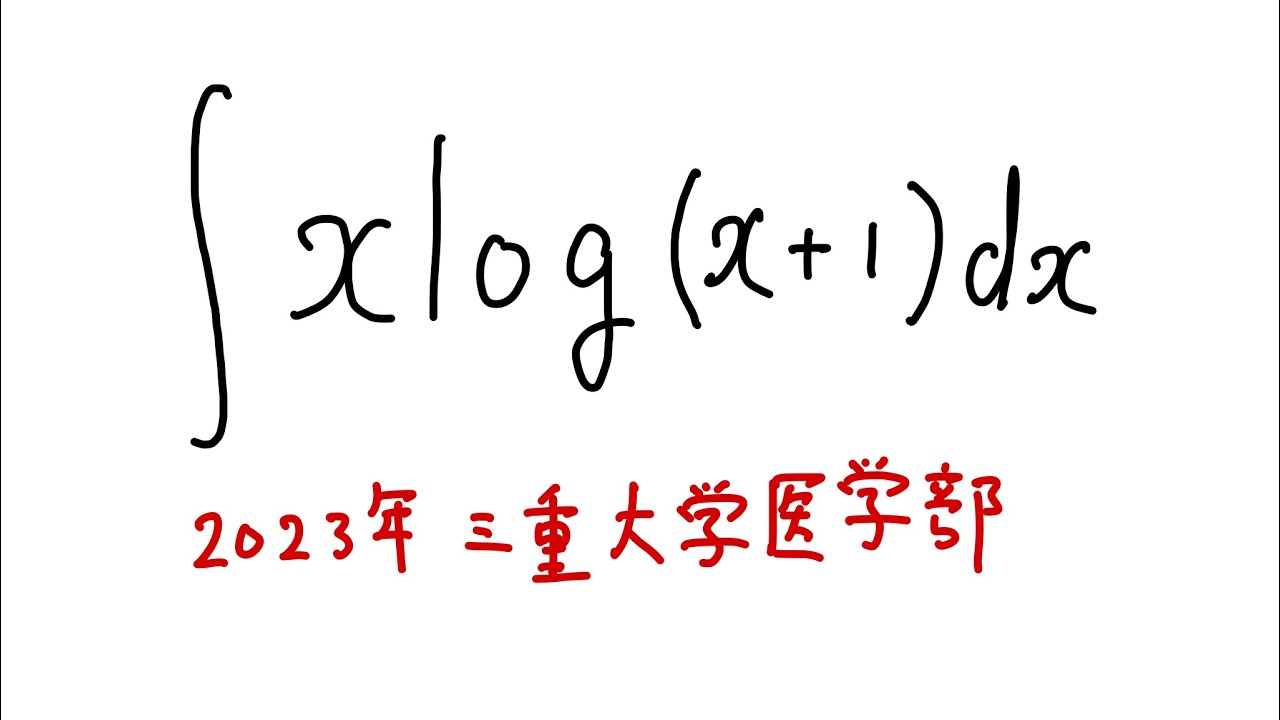
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
#明治大学2023#極限_48
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
この動画を見る
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
#三重大学医学部2023#不定積分_47
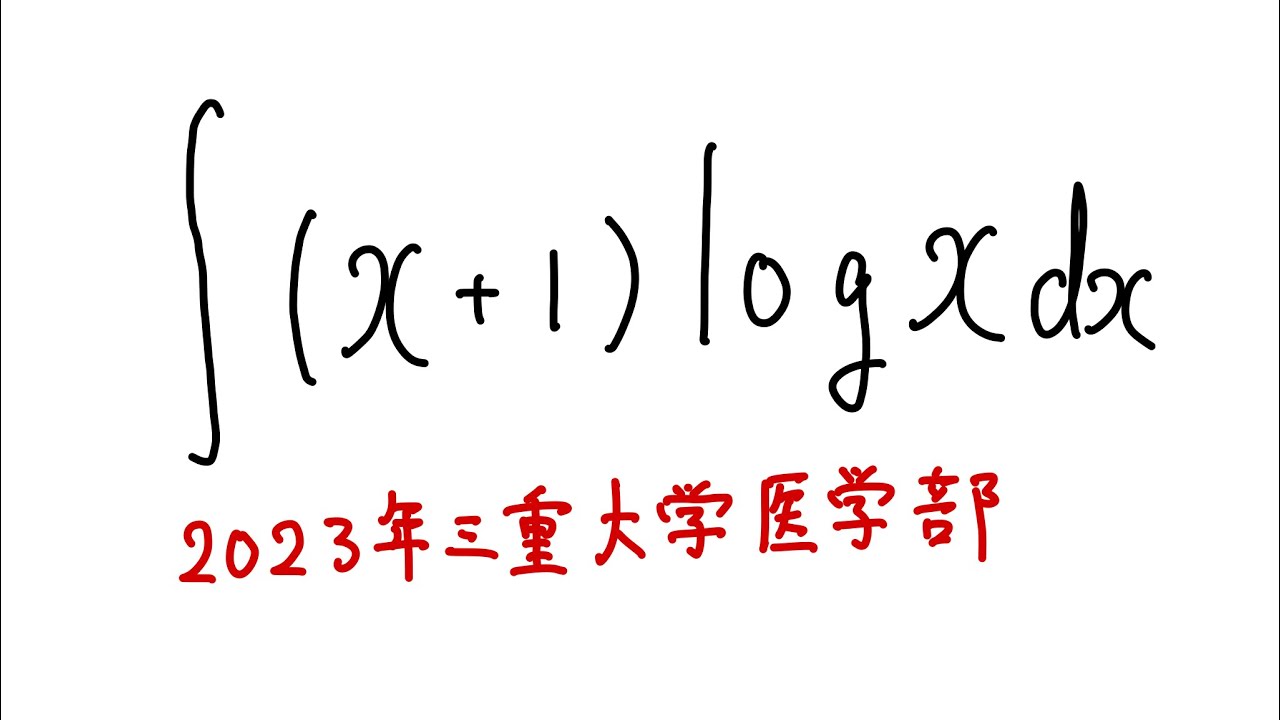
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} (x+1)\log x \ dx$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} (x+1)\log x \ dx$
を解け.
2023三重大学医学部過去問題
#産業医科大学2024#定積分_46
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} \sqrt{3-x^2+2x}\ dx$
を解け.
2024産業医科大学過去問題
この動画を見る
$\displaystyle \int_{-1}^{1} \sqrt{3-x^2+2x}\ dx$
を解け.
2024産業医科大学過去問題
#島根大学2019#不定積分_44
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} (\sin x)^{2018} \cos x \ dx$
を解け.
2019島根大学過去問題
この動画を見る
$\displaystyle \int_{}^{} (\sin x)^{2018} \cos x \ dx$
を解け.
2019島根大学過去問題
#産業医科大学2023#定積分_43
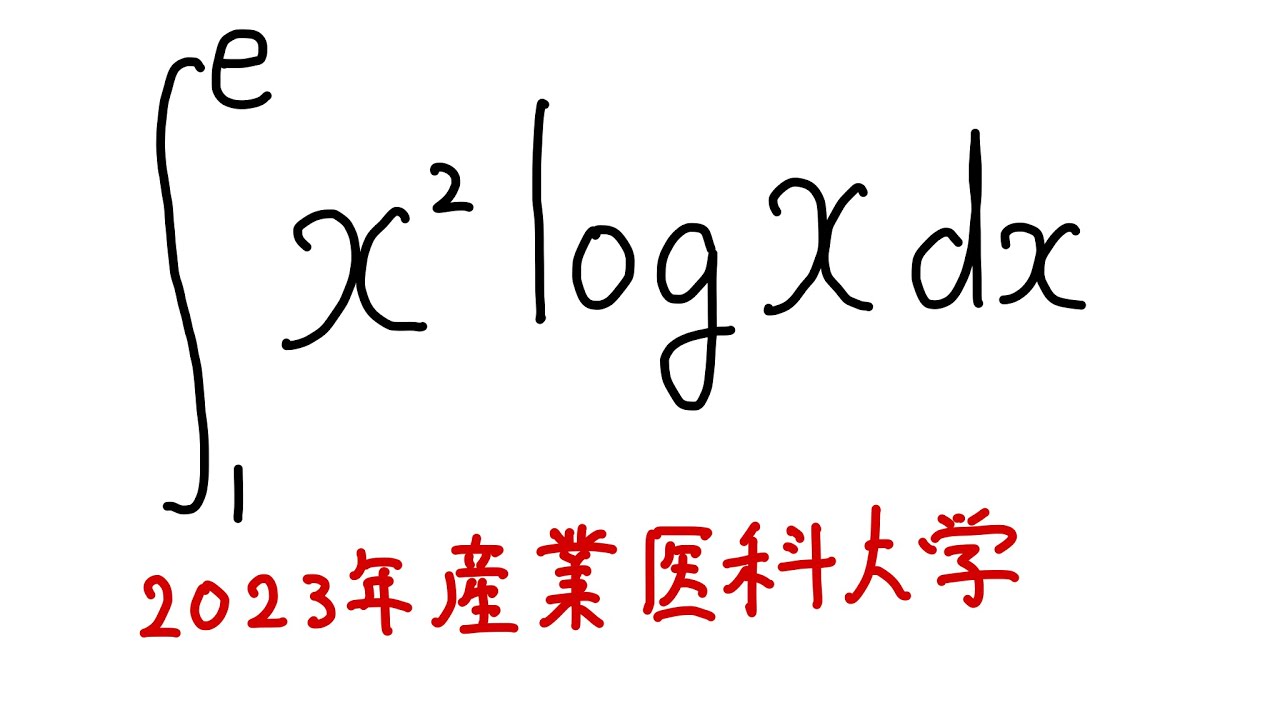
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e} x^2\log x \ dx$を解け.
2023産業医科大学過去問題
この動画を見る
$\displaystyle \int_{1}^{e} x^2\log x \ dx$を解け.
2023産業医科大学過去問題
#島根大学2024#不定積分_42
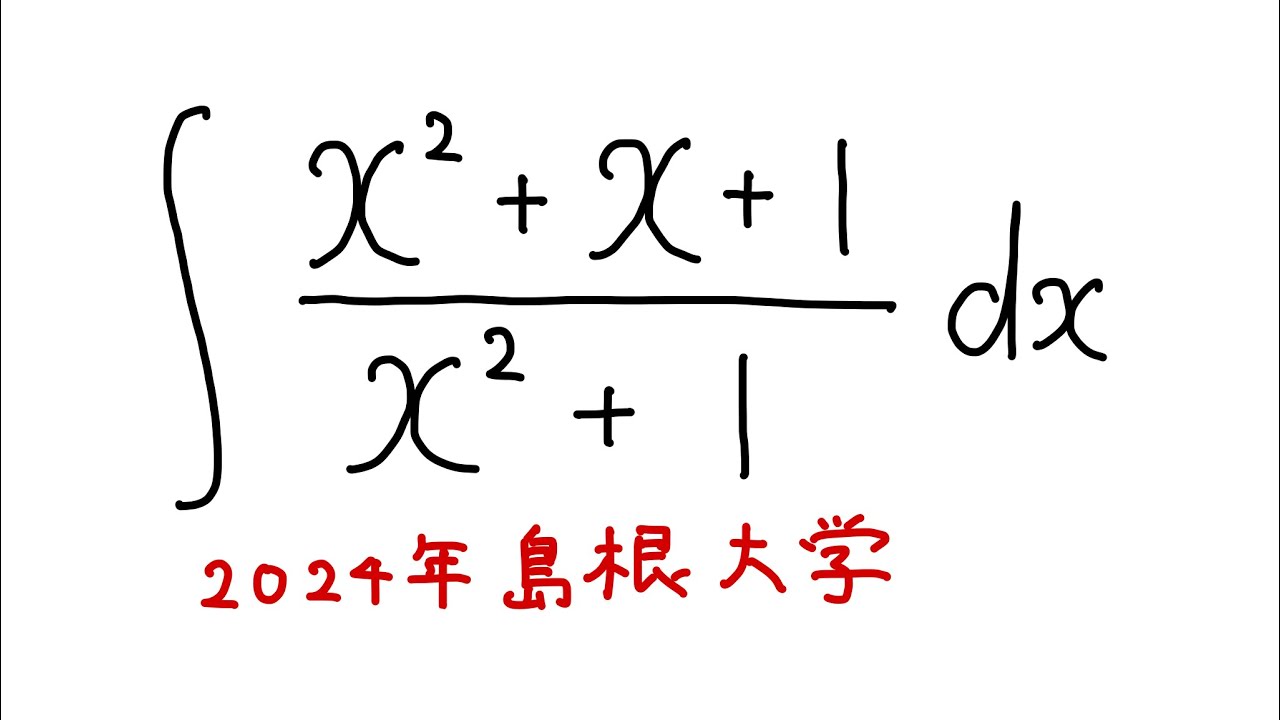
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{x^2+x+1}{x^2+1}dx$
を解け.
2024島根大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2+x+1}{x^2+1}dx$
を解け.
2024島根大学過去問題
#産業医科大学2024#区分級積法_41
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.
2022産業医科大学過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.
2022産業医科大学過去問題
激ムズ積分 大技で卍固め By BBBさん
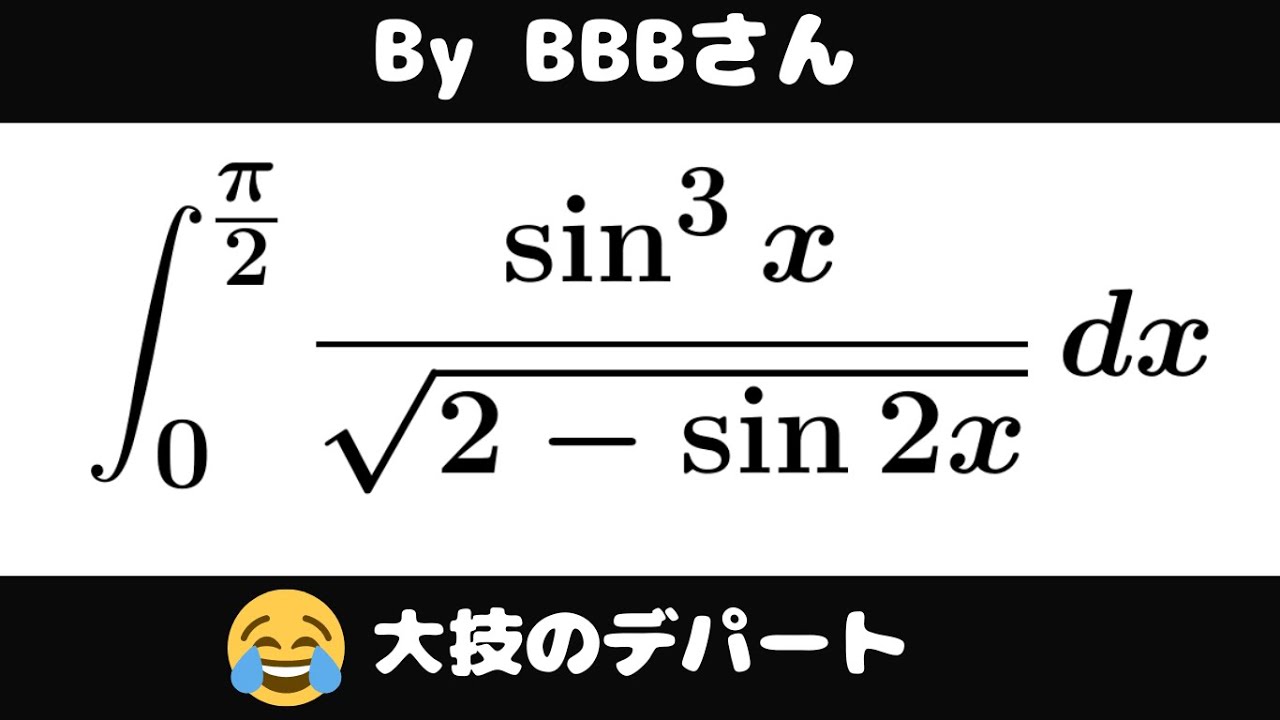
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \dfrac{\sin^3x}{\sqrt{2-\sin 2x}}dx$
を解け.
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \dfrac{\sin^3x}{\sqrt{2-\sin 2x}}dx$
を解け.
#関西大学2024#不定積分_40
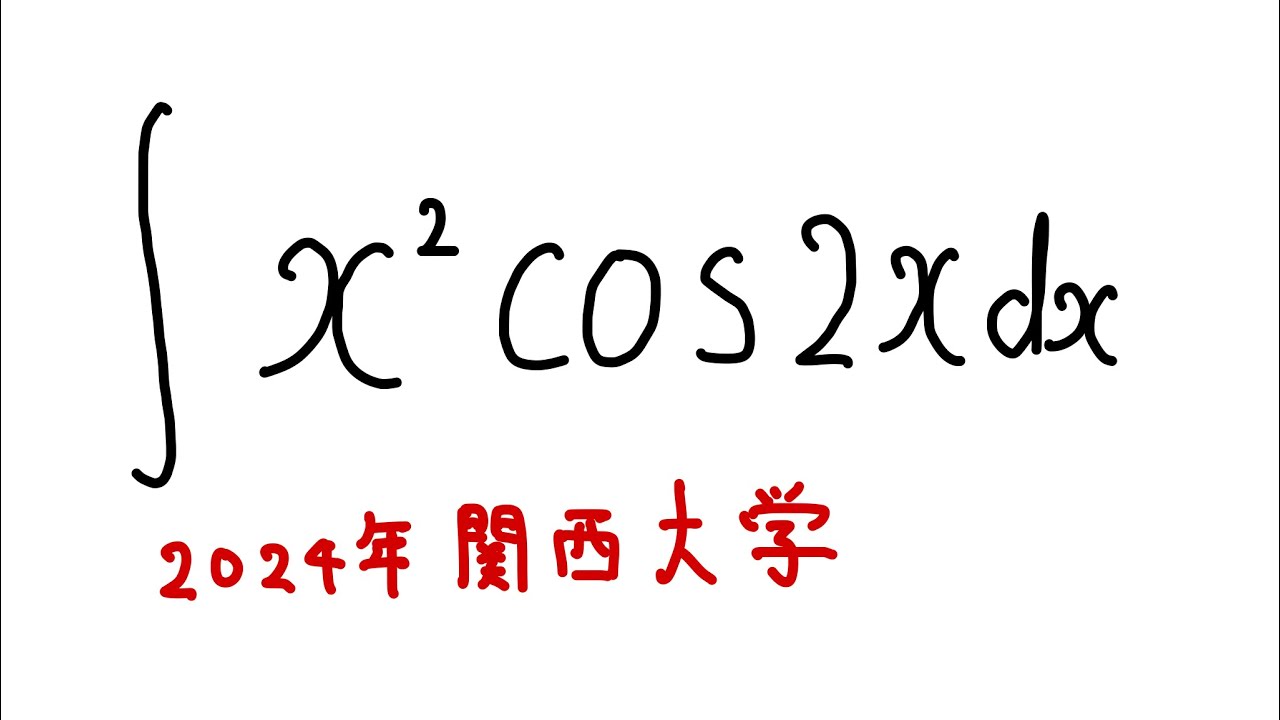
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x^2\cos \ 2x\ dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} x^2\cos \ 2x\ dx$
を解け.
2022関西大学過去問題
#関西大学2022#不定積分_39
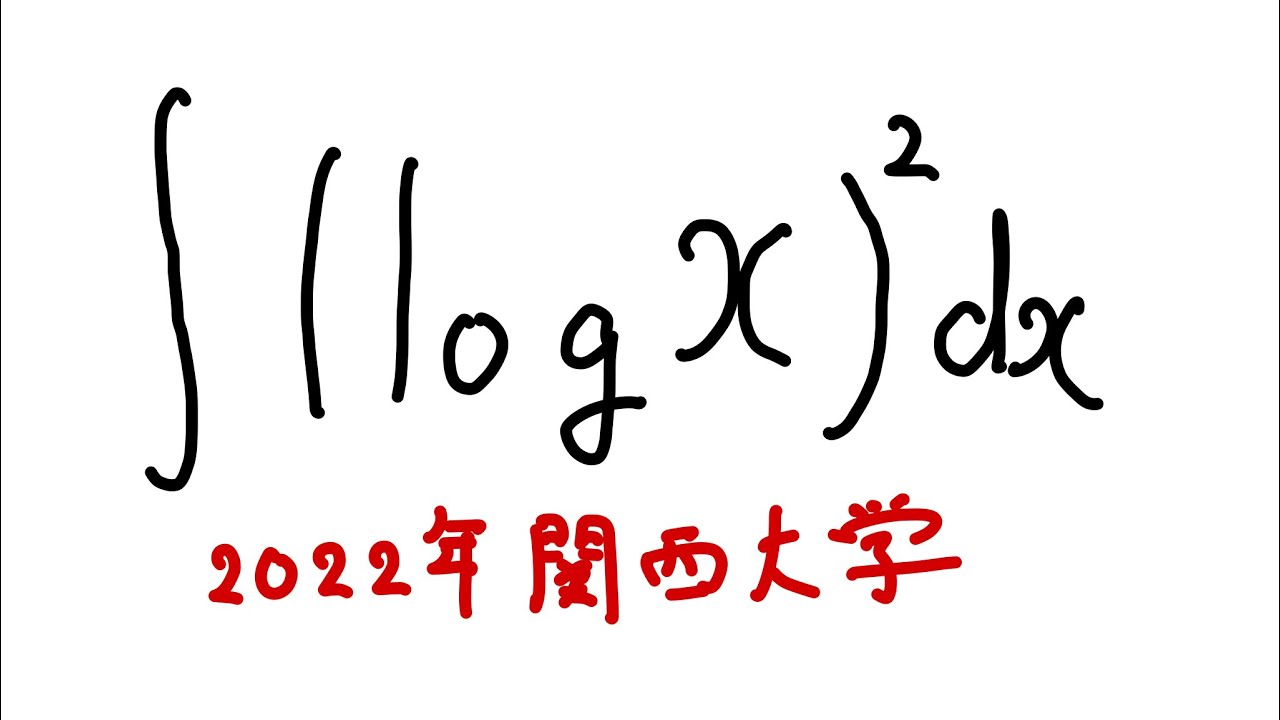
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} (\log x^2 )dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} (\log x^2 )dx$
を解け.
2022関西大学過去問題
大学入試問題#925「初手が見えれば一直線」 #関西大学2023
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \left(\dfrac{1}{\sqrt x}\ \sin\ (3\sqrt x)\ \cos \ (5\sqrt x)\right)dx$
を解け.
2023関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \left(\dfrac{1}{\sqrt x}\ \sin\ (3\sqrt x)\ \cos \ (5\sqrt x)\right)dx$
を解け.
2023関西大学過去問題
#関西大学2022#定積分_38
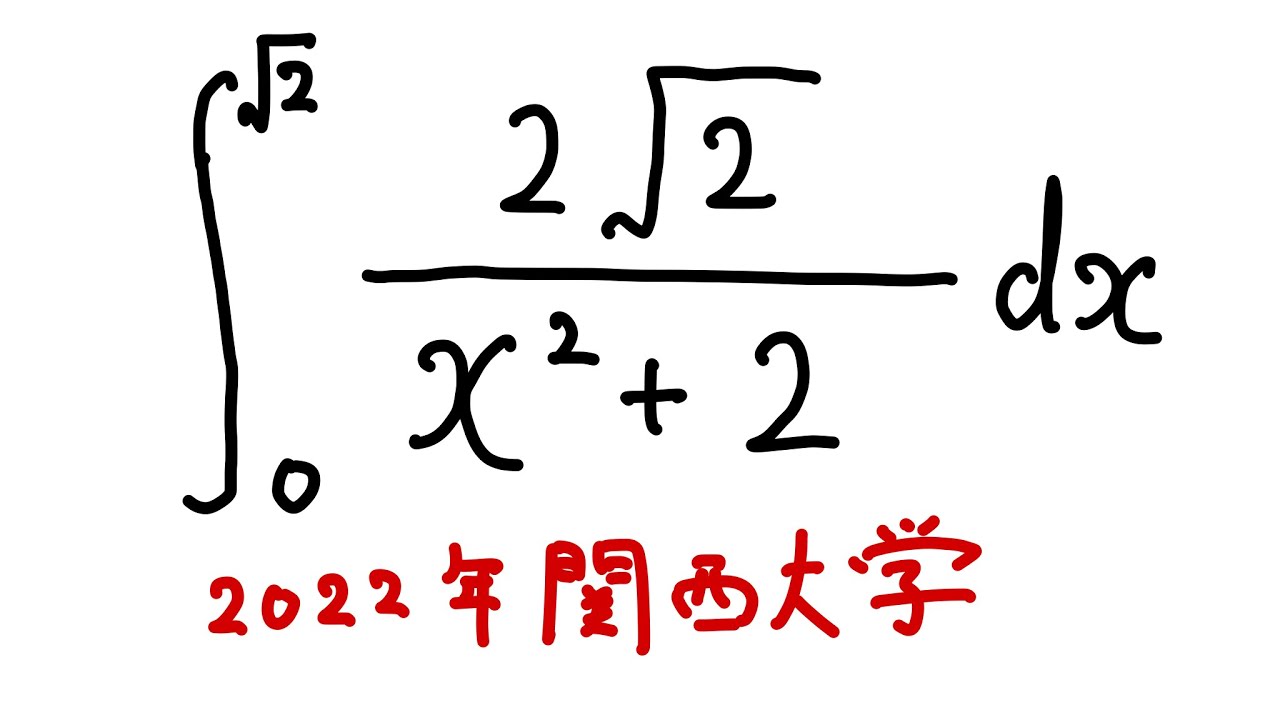
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\sqrt2} \dfrac{2\sqrt2}{x^2+2}dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt2} \dfrac{2\sqrt2}{x^2+2}dx$
を解け.
2022関西大学過去問題
福田の数学〜明治大学2024全学部統一III第1問(2)〜定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
この動画を見る
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
福田の数学〜明治大学2024全学部統一III第1問(2)〜定積分の計算
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx$
この動画を見る
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx$
福田の数学〜明治大学2024全学部統一III第1問(1)〜合成関数の微分計算
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle
\dfrac{d}{dx}\log{(x+\sqrt{1+x^2})}
$
この動画を見る
$\displaystyle
\dfrac{d}{dx}\log{(x+\sqrt{1+x^2})}
$
福田のおもしろ数学241〜e^πとπ^eの大小
