数Ⅱ
数Ⅱ
福田の数学〜上智大学2024TEAP利用型理系第1問(3)〜対数不等式を満たす最小の整数
単元：
#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
この動画を見る
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
福田のおもしろ数学265〜直交する2つの円柱の共通部分の体積
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
x軸、y軸を軸とする半径1の円柱T_1 , \ T_2の共通部分の体積を求めよ。$（図は動画参照）
この動画を見る
$
x軸、y軸を軸とする半径1の円柱T_1 , \ T_2の共通部分の体積を求めよ。$（図は動画参照）
福田のおもしろ数学264〜なぜ球の表面積は4πr^3なのかの証明
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
半径$r$の球の体積が$\frac{4πr^3}{3}$あることを既知として、表面積が$4πr^2$であることを証明して下さい。
この動画を見る
半径$r$の球の体積が$\frac{4πr^3}{3}$あることを既知として、表面積が$4πr^2$であることを証明して下さい。
福田の数学〜上智大学2024TEAP利用型文系第3問(4)〜線分の通過範囲の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#軌跡と領域#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
この動画を見る
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
福田の数学〜上智大学2024TEAP利用型文系第3問(3)〜直線の回転
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
この動画を見る
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(1)〜対数指数不等式と領域に含まれる格子点の個数
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
この動画を見る
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
福田のおもしろ数学260〜関数方程式を満たす関数を探せ
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
微分可能な関数 $f(x)$ はすべての実数 $x,y$ に対し
$f(x^2-y^2)$$=xf(x)-yf(y)$ $\cdots$ ① を満たす。このような $f(x)$ をすべて求めて下さい。
この動画を見る
微分可能な関数 $f(x)$ はすべての実数 $x,y$ に対し
$f(x^2-y^2)$$=xf(x)-yf(y)$ $\cdots$ ① を満たす。このような $f(x)$ をすべて求めて下さい。
#同志社大学2021#定積分_62
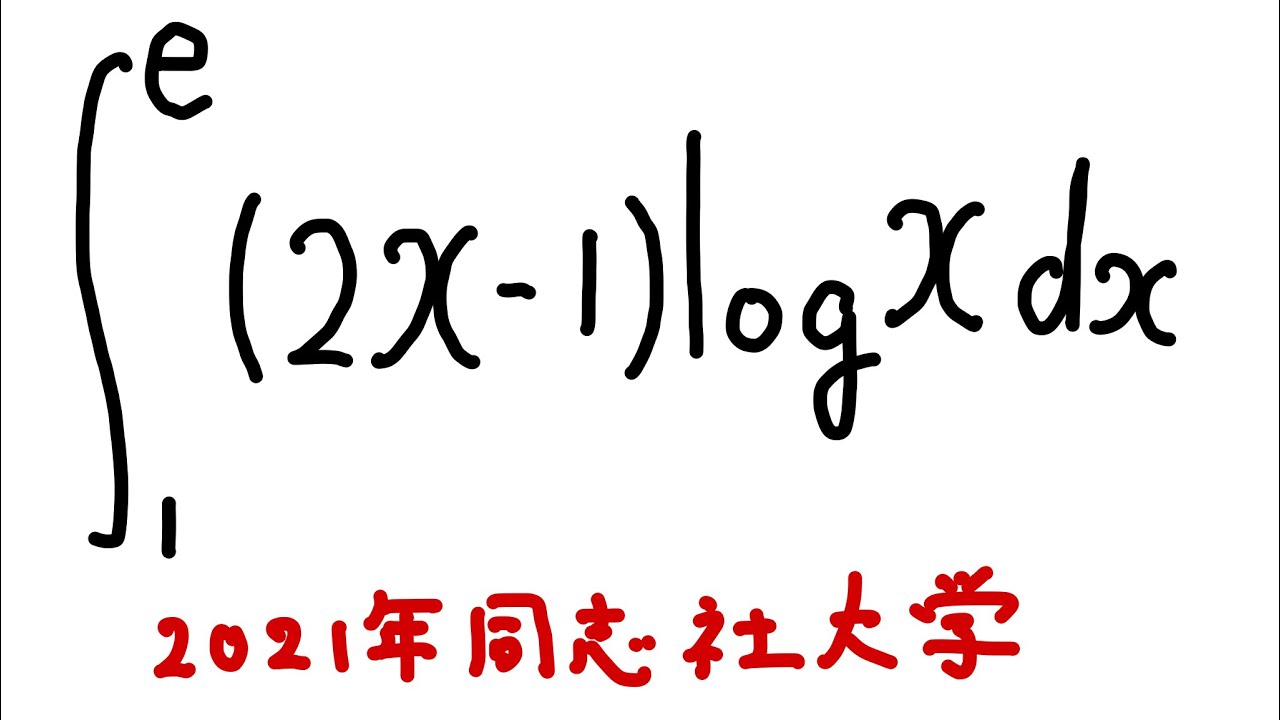
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#同志社大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e} (2x-1)\log x \ dx$を解け.
2021同志社大学過去問題
この動画を見る
$\displaystyle \int_{1}^{e} (2x-1)\log x \ dx$を解け.
2021同志社大学過去問題
#福岡大学医学部2018#極限_61
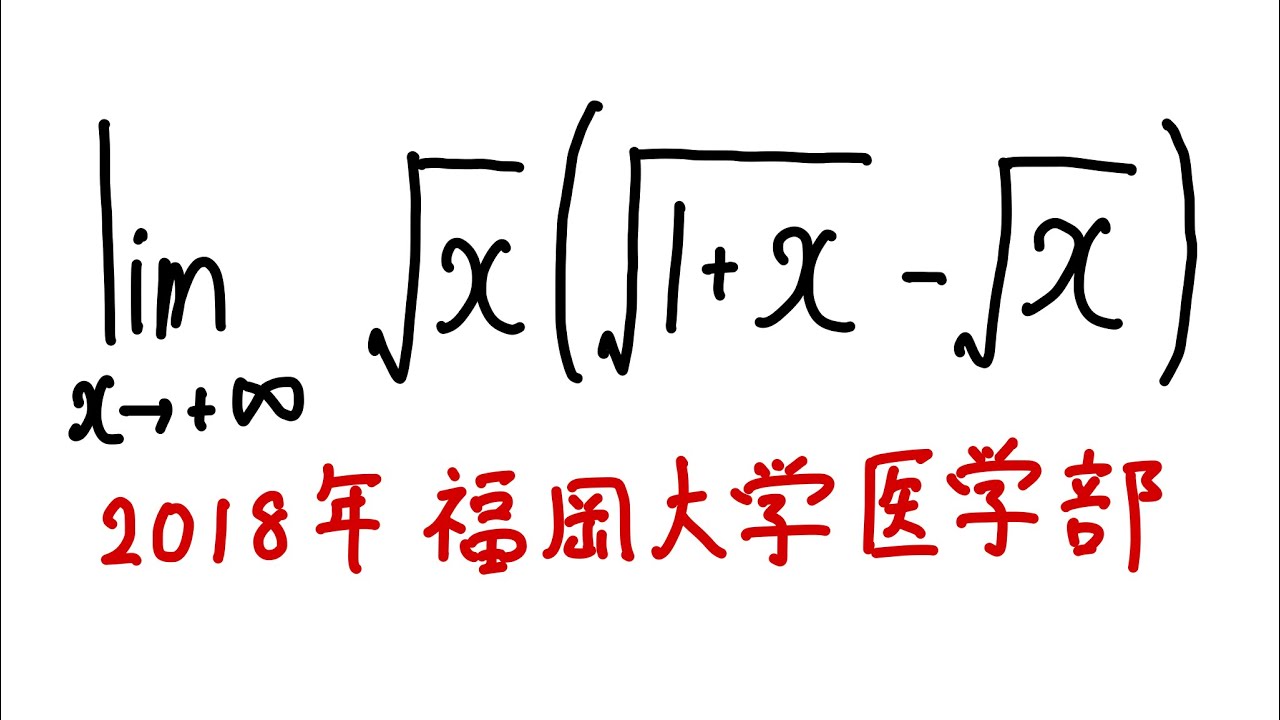
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \sqrt x \left(\sqrt{1+x}-\sqrt x \right)$を解け.
2018福岡大学医学部過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} \sqrt x \left(\sqrt{1+x}-\sqrt x \right)$を解け.
2018福岡大学医学部過去問題
うおおおおお！ 東京都市大学(武蔵工業大学)2004 大学入試問題#934
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#武蔵工業大学
指導講師：
ますただ
問題文全文(内容文)：
連続関数$f(x)$で
$f(x)=e^x \displaystyle \int_{0}^{1} \{f(t)\}^2 dt$
を満たすものを求めよ.
2004東京都市大学過去問題
この動画を見る
連続関数$f(x)$で
$f(x)=e^x \displaystyle \int_{0}^{1} \{f(t)\}^2 dt$
を満たすものを求めよ.
2004東京都市大学過去問題
#京都帝国大学1935#不定積分_60
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^2}}dx$を解け.
1935京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^2}}dx$を解け.
1935京都帝国大学過去問題
#京都大学1937#極限_59
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
福田のおもしろ数学258〜三角関数の積を計算
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \prod_{k=0}^n \cos (2^k \theta)$ を計算せよ。
この動画を見る
$\displaystyle \prod_{k=0}^n \cos (2^k \theta)$ を計算せよ。
#弘前大学2023#定積分_58
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
#弘前大学2023#定積分_57
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
福田のおもしろ数学257〜3変数の不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c>0$, $abc=1$ のとき
\begin{equation*}
\left(a-1+\frac{1}{b}\right) \left(b-1+\frac{1}{c}\right) \left(c-1+\frac{1}{a}\right) \leq 1
\end{equation*}
を証明して下さい。
この動画を見る
$a,b,c>0$, $abc=1$ のとき
\begin{equation*}
\left(a-1+\frac{1}{b}\right) \left(b-1+\frac{1}{c}\right) \left(c-1+\frac{1}{a}\right) \leq 1
\end{equation*}
を証明して下さい。
京大らしさ全開の不朽の名作 京都帝国大学1937 大学入試問題#932
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
#弘前大学2024#定積分_56
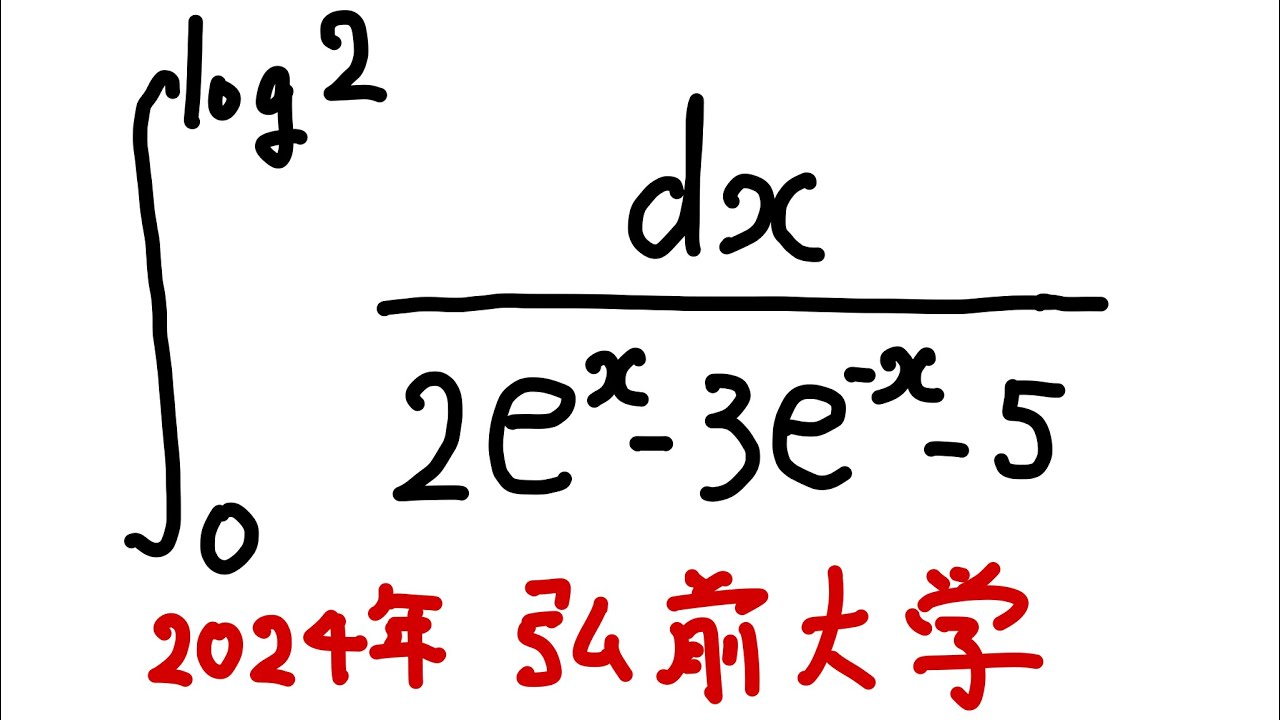
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
この動画を見る
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
#京都帝国大学1937#微分_55
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$y=e^{x^x}$なるとき,
$\dfrac{dy}{dx}$を求めよ.
1937京都帝国大学過去問題
この動画を見る
$y=e^{x^x}$なるとき,
$\dfrac{dy}{dx}$を求めよ.
1937京都帝国大学過去問題
福田の数学〜青山学院大学2024理工学部第3問〜2次方程式の解の条件と領域
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
福田次郎
問題文全文(内容文)：
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
この動画を見る
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
#京都大学1937#不定積分_54
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^6}}dx$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^6}}dx$を解け.
1937京都帝国大学過去問題
#電気通信大学2024#不定積分_53
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} e^x \sqrt{6-e^x} dx$を解け.
2024電気通信大学過去問題
この動画を見る
$\displaystyle \int_{}^{} e^x \sqrt{6-e^x} dx$を解け.
2024電気通信大学過去問題
突破口を探す不定積分 京都帝国大学1936 大学入試問題#931
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$ \sec \ x=\dfrac{1}{\cos x}$とする.
$\displaystyle \int_{}^{} \sec \ x \ \tan^2 x \ dx$を解け.
1936京都帝国大学過去問題
この動画を見る
$ \sec \ x=\dfrac{1}{\cos x}$とする.
$\displaystyle \int_{}^{} \sec \ x \ \tan^2 x \ dx$を解け.
1936京都帝国大学過去問題
#京都帝国大学1935#不定積分_52
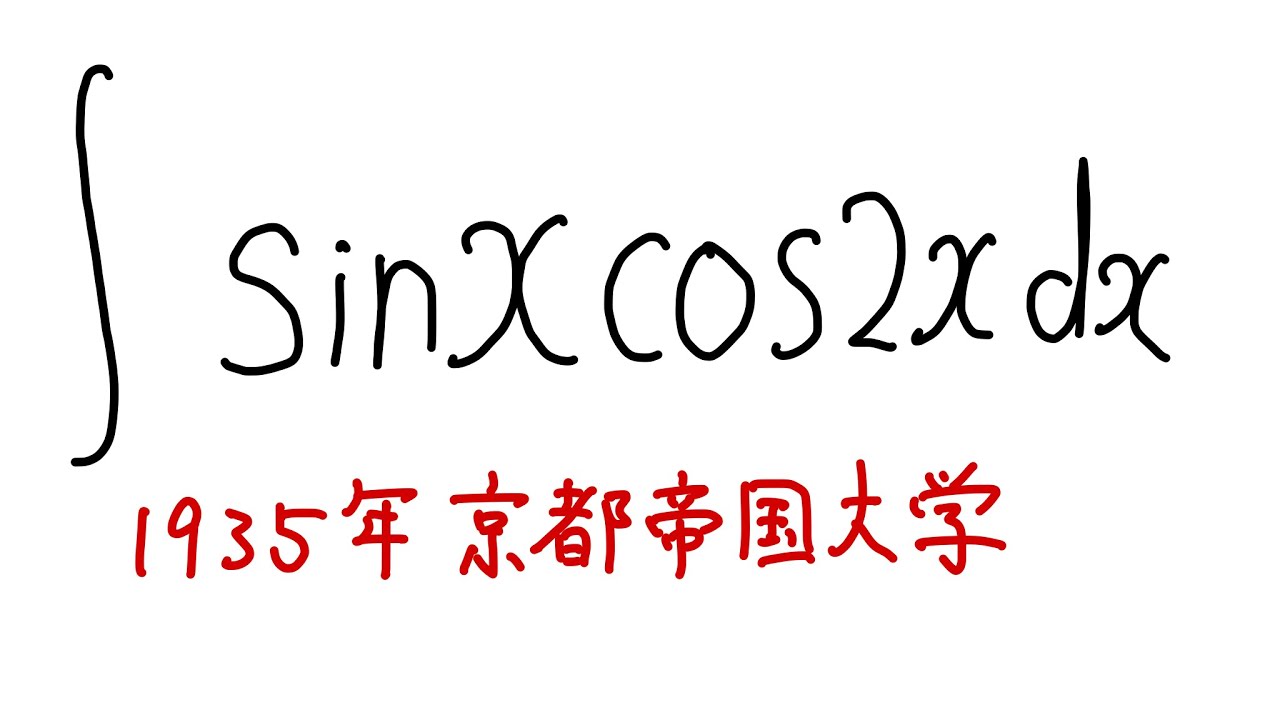
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} \sin x \ \cos 2x \ dx$を解け.
1935京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \sin x \ \cos 2x \ dx$を解け.
1935京都帝国大学過去問題
#京都帝国大学1937#不定積分_51
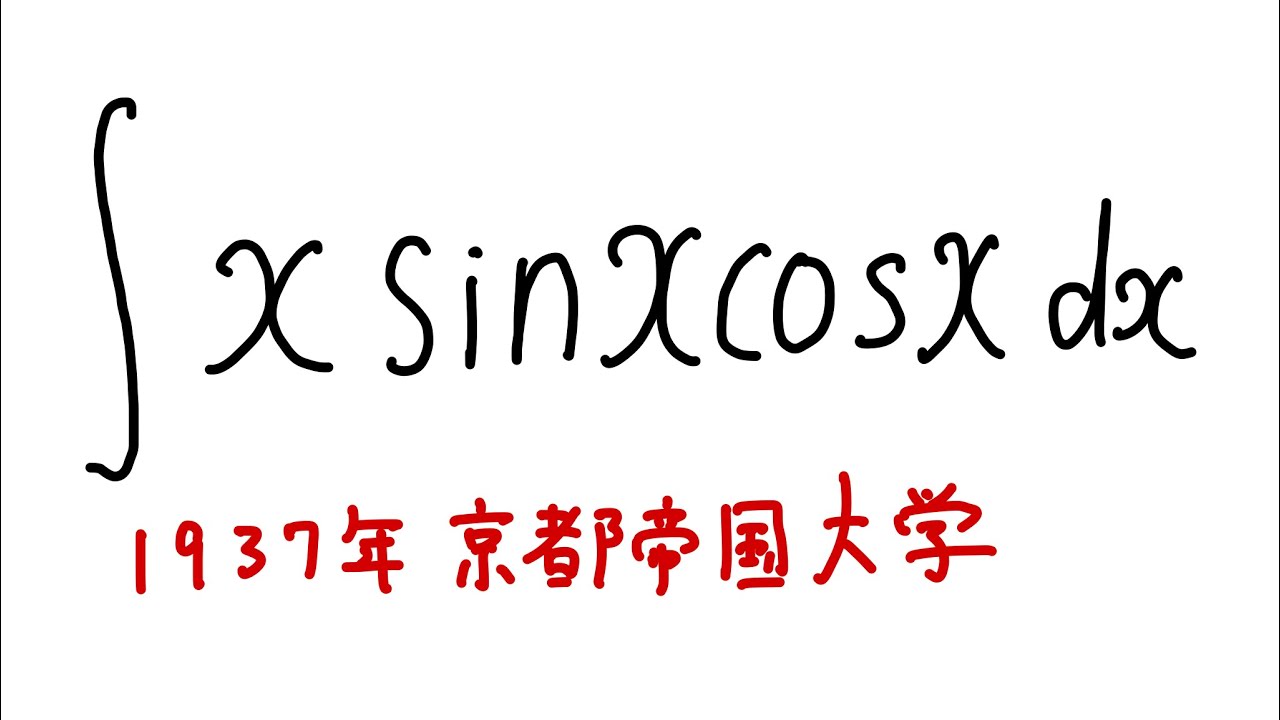
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x \ \sin x\ \cos x \ dx$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \sin x\ \cos x \ dx$を解け.
1937京都帝国大学過去問題
定積分の微分の基本問題 島根大学後期2024 大学入試問題#930
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#島根大学
指導講師：
ますただ
問題文全文(内容文)：
$a$の正の定数とする.
関数$g(x)$が,$x\gt 0$で定義された連続関数で,
次の等式をみたすとき,$g(x)$と$a$の値を求めよ.
$\displaystyle \int_{a}^{x^3} g(u) du =\log x$
2024島根大学後期過去問題
この動画を見る
$a$の正の定数とする.
関数$g(x)$が,$x\gt 0$で定義された連続関数で,
次の等式をみたすとき,$g(x)$と$a$の値を求めよ.
$\displaystyle \int_{a}^{x^3} g(u) du =\log x$
2024島根大学後期過去問題
#三重大学医学部2023#極限_50
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
#三重大学医学部2023#不定積分_49
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
よくある方程式
戦後の京都大学の入試いけんじゃね？ 京都大学医学部1946 大学入試問題#929
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^4-17x^2-34x-30=0$
なる方程式を解け.
1946京都大学医学部過去問題
この動画を見る
$x^4-17x^2-34x-30=0$
なる方程式を解け.
1946京都大学医学部過去問題