 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
大学入試問題#542「どこでも対称性が流行」 九州大学(2023) #高次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
ますただ
問題文全文(内容文):
$x^4-2x+3x^2-2x+1=0$を解け
出典:2023年九州大学 入試問題
この動画を見る
$x^4-2x+3x^2-2x+1=0$を解け
出典:2023年九州大学 入試問題
フツーにやっても出るけどね三次方程式解と係数の関係

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$としたとき、
次の3つを解にもつ3次方程式を作れ.
(1)$\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\delta}$
(2)$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$
この動画を見る
$x^3+2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$としたとき、
次の3つを解にもつ3次方程式を作れ.
(1)$\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\delta}$
(2)$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$
早稲田の恒等式!この形は〇〇したくなりますよね【早稲田大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
正の整数$m$,定数関数でない整式$P(x)$である.
$\displaystyle\int_{0}^{x} {P(t)}^m dt=P(x^3)-P(0)$
$P(x)$を求めよ.
早稲田大過去問
この動画を見る
正の整数$m$,定数関数でない整式$P(x)$である.
$\displaystyle\int_{0}^{x} {P(t)}^m dt=P(x^3)-P(0)$
$P(x)$を求めよ.
早稲田大過去問
福田の数学〜東北大学2023年理系第4問〜1の5乗根

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
ざ・整式の剰余 様々な解法

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整式$P(x)$を$(x-2)^2$で割るとあまりは$6x-1$であり,
$(x+1)$で割るとあまりは2である.
$P(x)$を$(x-2)^2(x+1)$で割ったあまりはいくつか?求めよ.
この動画を見る
整式$P(x)$を$(x-2)^2$で割るとあまりは$6x-1$であり,
$(x+1)$で割るとあまりは2である.
$P(x)$を$(x-2)^2(x+1)$で割ったあまりはいくつか?求めよ.
福田の数学〜東北大学2023年理系第2問〜三角方程式の解の個数とその極限

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
和子の数学的才能に鈴木貫太郎驚愕【n個の場合の相加相乗平均の華麗な証明】

単元:
#数Ⅱ#式と証明#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
鈴木貫太郎先生がn個の場合の相加相乗平均の証明を解説します。
問題の解き方を学んで、参考にしましょう!
この動画を見る
鈴木貫太郎先生がn個の場合の相加相乗平均の証明を解説します。
問題の解き方を学んで、参考にしましょう!
4次方程式の解と係数の関係?

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
この動画を見る
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
大学入試問題#537 京都府立医科大学2015 #整数問題

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#京都府立医科大学
指導講師:
ますただ
問題文全文(内容文):
(1)
$0 \lt a \lt b$とする
$a^b=b^a$のとき$1 \lt a \lt e \lt b$を示せ
(2)
$\sqrt{ 5 }^{\sqrt{ 7 }}$と$\sqrt{ 7 }^{\sqrt{ 5 }}$の大小を比較せよ
出典:2015年京都府立医科大学 入試問題
この動画を見る
(1)
$0 \lt a \lt b$とする
$a^b=b^a$のとき$1 \lt a \lt e \lt b$を示せ
(2)
$\sqrt{ 5 }^{\sqrt{ 7 }}$と$\sqrt{ 7 }^{\sqrt{ 5 }}$の大小を比較せよ
出典:2015年京都府立医科大学 入試問題
ただの整式の割り算

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(3x^3-4x^2+10x+4)^2$を$x^2-2x+4$で割ったあまりを求めよ.$
この動画を見る
$(3x^3-4x^2+10x+4)^2$を$x^2-2x+4$で割ったあまりを求めよ.$
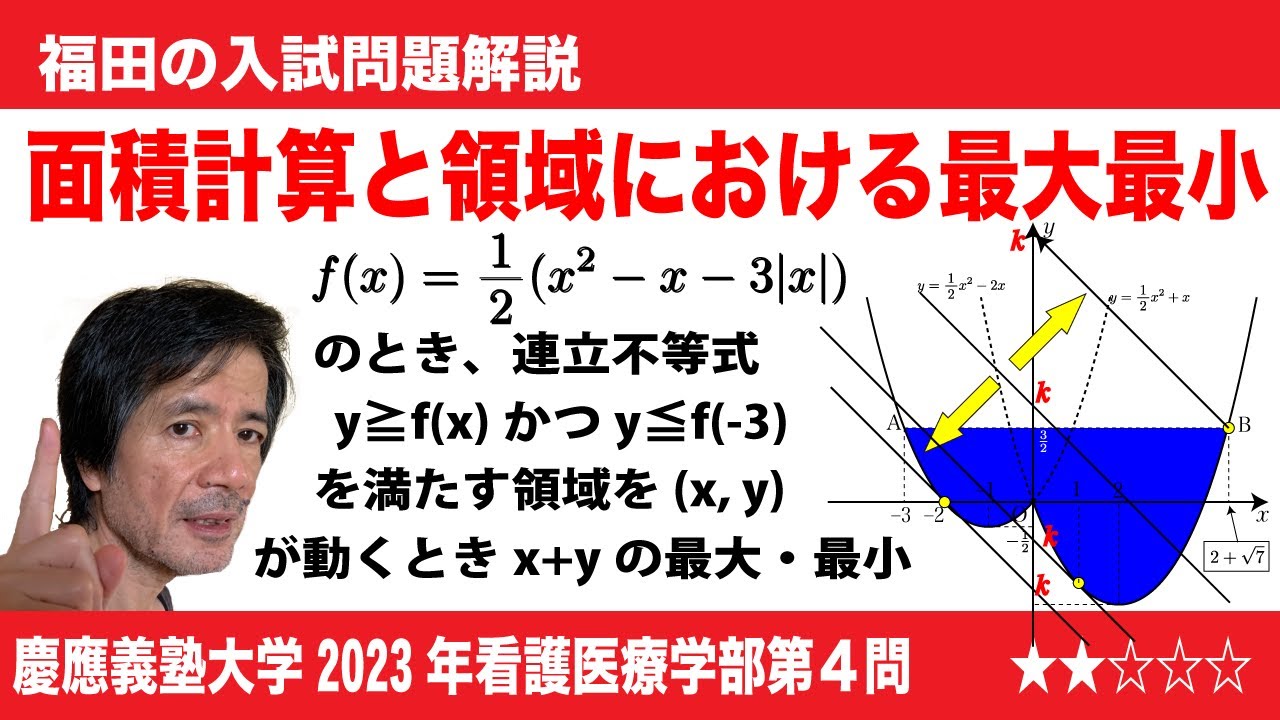
福田の数学〜慶應義塾大学2023年看護医療学部第4問〜絶対値の付いた関数と領域における最大最小
単元:
#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
大学入試問題#536「計算力大事」 福島県立医科大学(2021) #微積の応用

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ますただ
問題文全文(内容文):
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ
出典:2021年福島県立医科大学 入試問題
この動画を見る
すべての実数$x$に対して$f(x)=x+\displaystyle \int_{0}^{1} 2^{2t+x}f(t)\ dt$を満たすとき$f(0)$を求めよ
出典:2021年福島県立医科大学 入試問題
長崎大 複素数と整数の融合問題

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$を整数とする.
$\alpha=m+\sqrt7 ni$,
$\alpha^3=225+2\sqrt7 i$
(1)$x^3=1$を解け.
(2)$m,n$を求めよ.
(3)$Z^3=225+2\sqrt7 i$を解け.
長崎大過去問
この動画を見る
$m,n$を整数とする.
$\alpha=m+\sqrt7 ni$,
$\alpha^3=225+2\sqrt7 i$
(1)$x^3=1$を解け.
(2)$m,n$を求めよ.
(3)$Z^3=225+2\sqrt7 i$を解け.
長崎大過去問
埼玉大 直方体の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#埼玉大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
三辺の和が9cmで表面積が$48m^2$の直方体の体積の最大値を求めよ.
長崎大過去問
この動画を見る
三辺の和が9cmで表面積が$48m^2$の直方体の体積の最大値を求めよ.
長崎大過去問
埼玉大 3次不等式と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#指数関数と対数関数#微分法と積分法#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1)(n+1)^3\gt n^3+(n-1)^3$を満たす最大の整数$n$を求めよ.
(2)$n=(1)$の解,$x\gt 0$のとき
$(n+1)^{x+3}\gt n^{x+3}+(n-1)^{x+3}$を証明せよ.
埼玉大過去問
この動画を見る
$(1)(n+1)^3\gt n^3+(n-1)^3$を満たす最大の整数$n$を求めよ.
(2)$n=(1)$の解,$x\gt 0$のとき
$(n+1)^{x+3}\gt n^{x+3}+(n-1)^{x+3}$を証明せよ.
埼玉大過去問
【高校数学】条件付きの等式の証明~恒等式~ 1-9【数学Ⅱ】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の等式が成り立つことを証明せよ
$(1)a+b+c=0$のとき$a^2-2bc=b^2+c^2$
$\displaystyle(2)\frac{a}{b}=\frac{c}{d}$のとき$\displaystyle\frac{a+c}{b+d}=\frac{a-c}{b-d}$
この動画を見る
次の等式が成り立つことを証明せよ
$(1)a+b+c=0$のとき$a^2-2bc=b^2+c^2$
$\displaystyle(2)\frac{a}{b}=\frac{c}{d}$のとき$\displaystyle\frac{a+c}{b+d}=\frac{a-c}{b-d}$
福田の数学〜慶應義塾大学2023年看護医療学部第2問(1)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (1)0≦x≦π のとき、$\sqrt3\sin x$+$\cos x$=$\sqrt2$を解くと$x$=$\boxed{\ \ コ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (1)0≦x≦π のとき、$\sqrt3\sin x$+$\cos x$=$\sqrt2$を解くと$x$=$\boxed{\ \ コ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(5)〜整式の割り算の余り

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)整式P(x)を
P(x)=$\displaystyle\sum_{n=1}^{20}nx^n$=20$x^{20}$+19$x^{19}$+18$x^{18}$+...+2$x^2$+$x$
と定める。このとき、P(x)をx-1で割った時の余りは$\boxed{\ \ ク\ \ }$である。
また、P(x)を$x^2$-1で割った時の余りは$\boxed{\ \ ケ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (5)整式P(x)を
P(x)=$\displaystyle\sum_{n=1}^{20}nx^n$=20$x^{20}$+19$x^{19}$+18$x^{18}$+...+2$x^2$+$x$
と定める。このとき、P(x)をx-1で割った時の余りは$\boxed{\ \ ク\ \ }$である。
また、P(x)を$x^2$-1で割った時の余りは$\boxed{\ \ ケ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
神戸大 3次関数の最大最小

単元:
#大学入試過去問(数学)#式と証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
この動画を見る
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(4)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)($\log_29$)($\log_3x$)-$\log_25$=2 を解くとx=$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (4)($\log_29$)($\log_3x$)-$\log_25$=2 を解くとx=$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(3)〜解と係数の関係

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)2次方程式$x^2$+$x$+3=0 の2つの解を$\alpha$、$\beta$とするとき、
$\frac{\beta}{\alpha}$+$\frac{\alpha}{\beta}$=$\boxed{\ \ オ\ \ }$であり、$\frac{\beta^2}{\alpha}$+$\frac{\alpha^2}{\beta}$=$\boxed{\ \ カ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (3)2次方程式$x^2$+$x$+3=0 の2つの解を$\alpha$、$\beta$とするとき、
$\frac{\beta}{\alpha}$+$\frac{\alpha}{\beta}$=$\boxed{\ \ オ\ \ }$であり、$\frac{\beta^2}{\alpha}$+$\frac{\alpha^2}{\beta}$=$\boxed{\ \ カ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
対数と不等式

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
この動画を見る
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
2打数1安打VS 3打数2安打 証明しろといわれたら数II

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
0<a<bのとき
$\frac{a}{b}$と$\frac{a+1}{b+1}$
どっちが大きい?
この動画を見る
0<a<bのとき
$\frac{a}{b}$と$\frac{a+1}{b+1}$
どっちが大きい?
相加相乗平均のエレガントな証明2通り
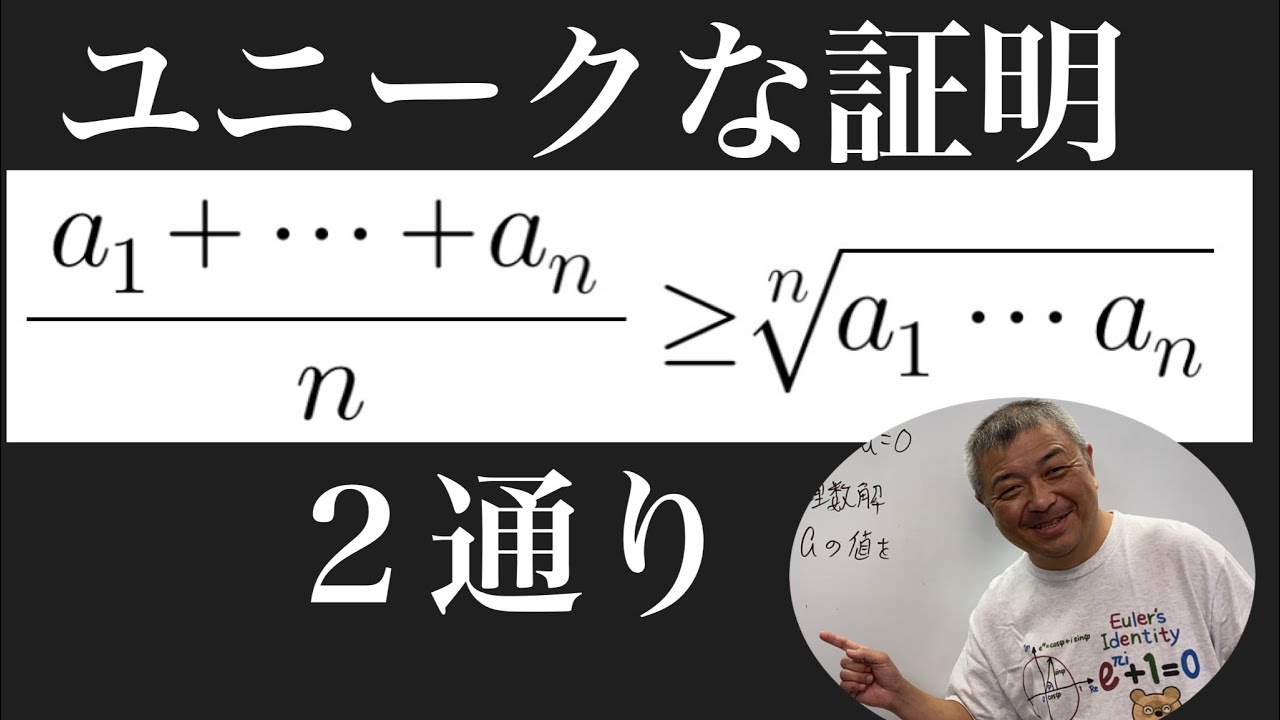
単元:
#数Ⅱ#式と証明#指数関数と対数関数#指数関数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{a_1+a_2+・・・・+a_n}{n}\geqq \sqrt[n]{a_1,a_2・・・・a_n}$
これを求めよ.
この動画を見る
$ \dfrac{a_1+a_2+・・・・+a_n}{n}\geqq \sqrt[n]{a_1,a_2・・・・a_n}$
これを求めよ.
整数問題が苦手な人は要チェック!絶対に取りたい整数問題【関西医科大学】【数学 入試問題】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
( 1) (a + 1)(a - 1)(b + 1)(b - 1) - 4ab を因数分解せよ。
( 2) (a + 1)(a - 1)(b + 1)(b - 1) = 4ab を満たす整数a,bの組で、 a < b の条件を満たすものは
?組あり、そのなかでa,bのどちらも正の整数となる組(a,b) は ?である 。
(2023年 関西医科大学)
この動画を見る
( 1) (a + 1)(a - 1)(b + 1)(b - 1) - 4ab を因数分解せよ。
( 2) (a + 1)(a - 1)(b + 1)(b - 1) = 4ab を満たす整数a,bの組で、 a < b の条件を満たすものは
?組あり、そのなかでa,bのどちらも正の整数となる組(a,b) は ?である 。
(2023年 関西医科大学)
神戸大 不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
この動画を見る
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
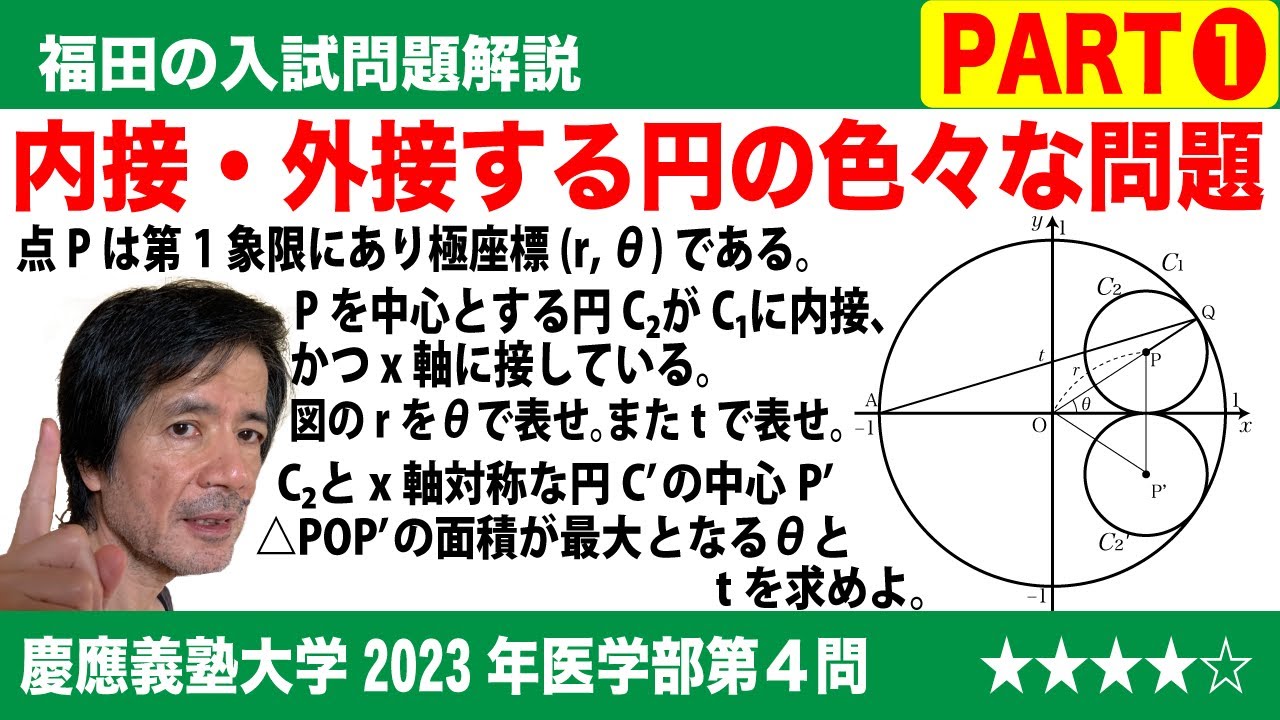
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
愛が1番!

i=1⁉️からくりは通常動画で❗️ #short

福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
