 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
指数方程式の基本問題

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{8^x+27^x}{12^x+18^x}=\dfrac{7}{6}$
これを解け(実数解)
この動画を見る
$ \dfrac{8^x+27^x}{12^x+18^x}=\dfrac{7}{6}$
これを解け(実数解)
指数法則の利用
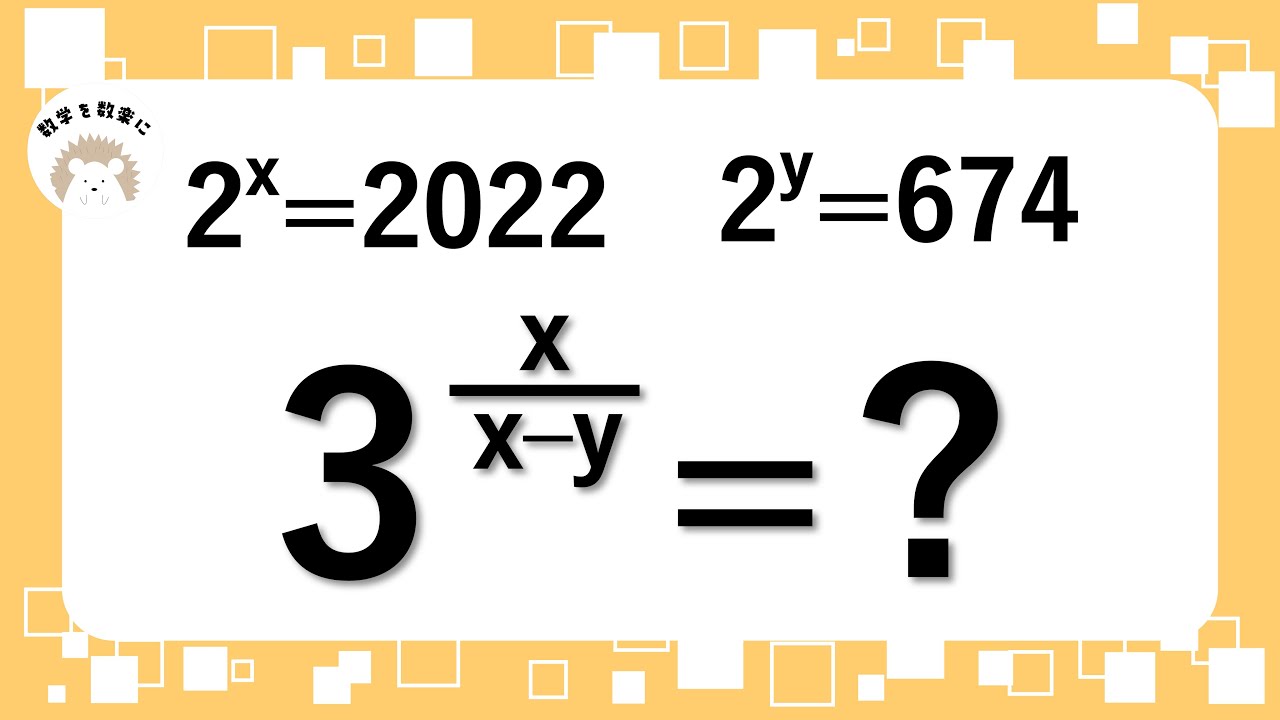
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^x=2022$ , $2^y=674$
$3^{\frac{x}{x-y}} =?$
この動画を見る
$2^x=2022$ , $2^y=674$
$3^{\frac{x}{x-y}} =?$
簡単すぎた

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 5^x=0.5^y=10000$である.
$\dfrac{1}{x}-\dfrac{1}{y}$はいくつであるか求めよ.
この動画を見る
$ 5^x=0.5^y=10000$である.
$\dfrac{1}{x}-\dfrac{1}{y}$はいくつであるか求めよ.
簡単すぎた

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5^x=0.5^y=10000$
$\dfrac{1}{x}-\dfrac{1}{y}=?$
この動画を見る
$5^x=0.5^y=10000$
$\dfrac{1}{x}-\dfrac{1}{y}=?$
大学入試問題#164 防衛医科大学(2020) 指数の計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$1 \leqq m,n$実数
$m^{\frac{n}{3}}+m^{-\frac{n}{3}}=\displaystyle \frac{3\sqrt{ 2 }}{2}$のとき
$mm^n-m^{-n}$の値を求めよ。
出典:2020年防衛医科大学 入試問題
この動画を見る
$1 \leqq m,n$実数
$m^{\frac{n}{3}}+m^{-\frac{n}{3}}=\displaystyle \frac{3\sqrt{ 2 }}{2}$のとき
$mm^n-m^{-n}$の値を求めよ。
出典:2020年防衛医科大学 入試問題
二項定理
基本問題
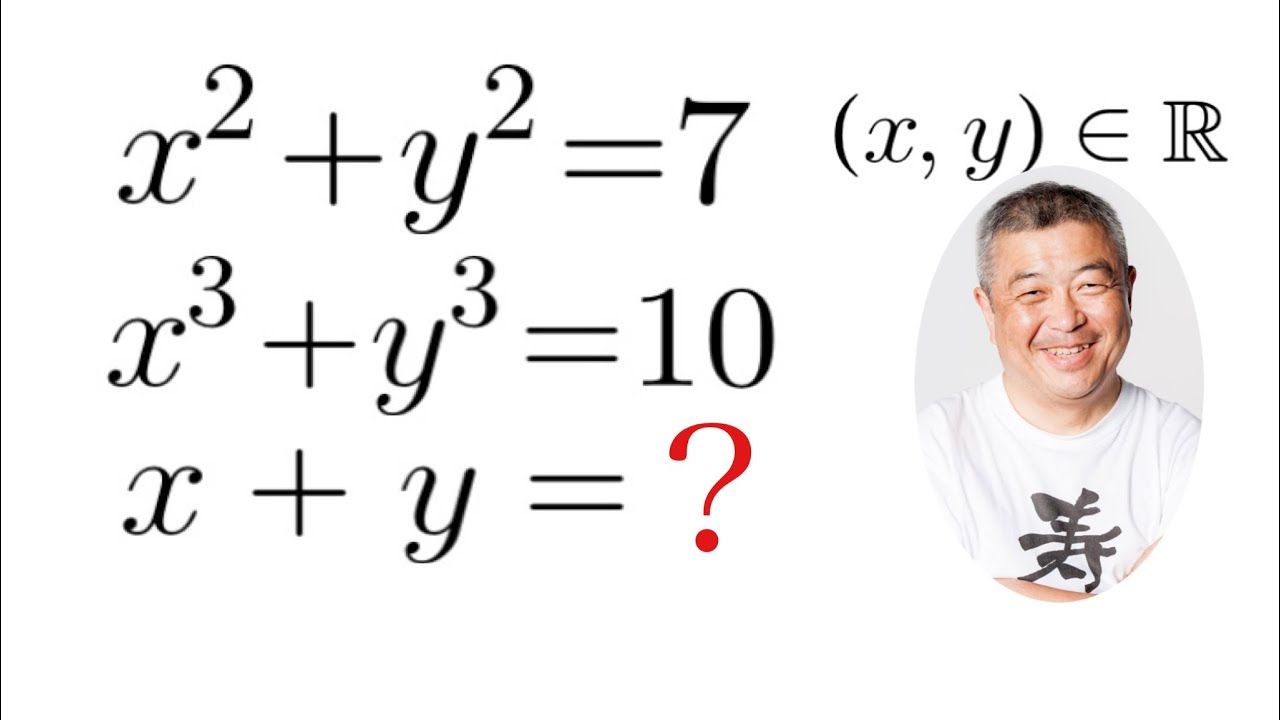
単元:
#数Ⅱ#式と証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yを実数とする.
$ x^2+y^2=7 $
$ x^3+y^3=10 $である.
x+yはいくつであるか求めよ.
この動画を見る
x,yを実数とする.
$ x^2+y^2=7 $
$ x^3+y^3=10 $である.
x+yはいくつであるか求めよ.
福田の数学〜東北大学2022年文系第3問〜領域における最大

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを正の実数とし、xy平面上の直線$l:ax;by-2=0$を考える。
(1)直線lと原点の距離が2以上であり、直線lと直線x=1の交点のy座標が
2以上であるような点(a,b)の取りうる範囲Dを求め、ab平面上に図示せよ。
(2)点(a,b)が(1)で求めた領域Dを動くとする。このとき、
$3a+2b$を最大にするa,bの値と$3a+2b$の最大値を求めよ。
2022東北大学文系過去問
この動画を見る
a,bを正の実数とし、xy平面上の直線$l:ax;by-2=0$を考える。
(1)直線lと原点の距離が2以上であり、直線lと直線x=1の交点のy座標が
2以上であるような点(a,b)の取りうる範囲Dを求め、ab平面上に図示せよ。
(2)点(a,b)が(1)で求めた領域Dを動くとする。このとき、
$3a+2b$を最大にするa,bの値と$3a+2b$の最大値を求めよ。
2022東北大学文系過去問
福田の数学〜名古屋大学2022年理系第1問〜割り算の余りと異なる実数解の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
この動画を見る
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
福田の数学・入試問題解説〜東北大学2022年文系第2問〜定積分で表された関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#不定積分・定積分#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数tの関数
$F(t)=\int_0^1|x^2-t^2|dx$
について考える。
(1)$0 \leqq t \leqq 1$のとき、$F(t)$をtの整式として表せ。
(2)$t \geqq 0$ のとき、F(t)を最小にするtの値TとF(T)の値を求めよ。
2022東北大学文系過去問
この動画を見る
実数tの関数
$F(t)=\int_0^1|x^2-t^2|dx$
について考える。
(1)$0 \leqq t \leqq 1$のとき、$F(t)$をtの整式として表せ。
(2)$t \geqq 0$ のとき、F(t)を最小にするtの値TとF(T)の値を求めよ。
2022東北大学文系過去問
大学入試問題#160 名古屋市立大学(2020) 三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq \pi$
$\cos4\theta=\cos2\theta$をみたす$\theta$をすべて求めよ。
出典:2020年名古屋市立大学 入試問題
この動画を見る
$0 \leqq \theta \leqq \pi$
$\cos4\theta=\cos2\theta$をみたす$\theta$をすべて求めよ。
出典:2020年名古屋市立大学 入試問題
3乗根の方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$ x^3+1=2\sqrt[3]{2x-1}$
この動画を見る
実数解を求めよ.
$ x^3+1=2\sqrt[3]{2x-1}$
【数Ⅱ】三角形の重心の軌跡【除外点に注意しよう】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
点Qが円$x^2+y^2=9$上を動くとき,
点$A(4,0)$と点Qを結ぶ線分AQの中点Pの軌跡を求めよ.
この動画を見る
点Qが円$x^2+y^2=9$上を動くとき,
点$A(4,0)$と点Qを結ぶ線分AQの中点Pの軌跡を求めよ.
【数学Ⅱ】繁分数式(分数の中に分数がある)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を簡単にせよ。
(1)$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
(1)$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
対数の基本問題(近似値は使えません)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$ \log_{10}2$が無理数であることを証明せよ.
(2)$2^{104}$は何桁か求めよ.
この動画を見る
(1)$ \log_{10}2$が無理数であることを証明せよ.
(2)$2^{104}$は何桁か求めよ.
指数の計算 log使わずに解ける

ハルハル様の作成問題 手筋連発

単元:
#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
この動画を見る
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
【わかりやすく】不等式の証明を解説(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不等式を証明せよ。
また、(2)で等号が成り立つのはどのようなときか。
(1)$x \gt 2,y \gt 3$のとき、$xy+6 \gt 3x+2y$
(2)$x^2+5y^2 \geqq 4xy$
この動画を見る
次の不等式を証明せよ。
また、(2)で等号が成り立つのはどのようなときか。
(1)$x \gt 2,y \gt 3$のとき、$xy+6 \gt 3x+2y$
(2)$x^2+5y^2 \geqq 4xy$
大学入試問題#158 名古屋市立大学(2020) 2項展開の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。
出典:2020年名古屋市立大学 入試問題
この動画を見る
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。
出典:2020年名古屋市立大学 入試問題
3乗根を外すだけ

単元:
#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
3乗根を外せ.
$ \sqrt[3]{\dfrac{10-7\sqrt2}{10+7\sqrt2}}$
この動画を見る
3乗根を外せ.
$ \sqrt[3]{\dfrac{10-7\sqrt2}{10+7\sqrt2}}$
【わかりやすく】等式の証明(数学Ⅱ/等式の証明)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の等式を証明せよ。
(1)$4ab=(a+b)^2-(a-b)^2$
(2)$(a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2$
この動画を見る
次の等式を証明せよ。
(1)$4ab=(a+b)^2-(a-b)^2$
(2)$(a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2$
解けるように作られた問題 ガウス少年なら一瞬

単元:
#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=\dfrac{25^x}{25^x+5}$である.
$ f \left(\dfrac{1}{100}\right)+f \left(\dfrac{2}{100}\right)+
・・・・・・+f \left(\dfrac{98}{100}\right)+\left(\dfrac{99}{100}\right)$の値を求めよ.
この動画を見る
$ f(x)=\dfrac{25^x}{25^x+5}$である.
$ f \left(\dfrac{1}{100}\right)+f \left(\dfrac{2}{100}\right)+
・・・・・・+f \left(\dfrac{98}{100}\right)+\left(\dfrac{99}{100}\right)$の値を求めよ.
福田の数学〜東京工業大学2022年理系第3問〜直角三角形の頂点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\alphaは0 \lt \alpha \lt \frac{\pi}{2}$を満たす実数とする。
$\angle A=\alpha$および$\angle P=\frac{\pi}{2}$を満たす直角三角形APB
が、次の2つの条件$(\textrm{a}),(\textrm{b})$を満たしながら、時刻t=0から時刻$t=\frac{\pi}{2}$まで
xy平面上を動くとする。
$(\textrm{a})$時刻tでの点A,Bの座標は、それぞれ$A(\sin t,0),B(0, \cos t)$である。
$(\textrm{b})$点Pは第一象限内にある。
このとき、次の問いに答えよ。
(1)点Pはある直線上を動くことを示し、その直線の方程式を$\alpha$を用いて表せ。
(2)時刻$t=0$から時刻$t=\frac{\pi}{2}$までの間に点Pが動く道のりを$\alpha$を用いて表せ。
(3)xy平面内において、連立不等式
$x^2-x+y^2 \lt 0, x^2+y^2-y \lt 0$
により定まる領域をDとする。このとき、点Pは領域Dには入らないことを示せ。
2022東京工業大学理系過去問
この動画を見る
$\alphaは0 \lt \alpha \lt \frac{\pi}{2}$を満たす実数とする。
$\angle A=\alpha$および$\angle P=\frac{\pi}{2}$を満たす直角三角形APB
が、次の2つの条件$(\textrm{a}),(\textrm{b})$を満たしながら、時刻t=0から時刻$t=\frac{\pi}{2}$まで
xy平面上を動くとする。
$(\textrm{a})$時刻tでの点A,Bの座標は、それぞれ$A(\sin t,0),B(0, \cos t)$である。
$(\textrm{b})$点Pは第一象限内にある。
このとき、次の問いに答えよ。
(1)点Pはある直線上を動くことを示し、その直線の方程式を$\alpha$を用いて表せ。
(2)時刻$t=0$から時刻$t=\frac{\pi}{2}$までの間に点Pが動く道のりを$\alpha$を用いて表せ。
(3)xy平面内において、連立不等式
$x^2-x+y^2 \lt 0, x^2+y^2-y \lt 0$
により定まる領域をDとする。このとき、点Pは領域Dには入らないことを示せ。
2022東京工業大学理系過去問
【数学Ⅱ/高2の予習】恒等式

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式が$x$についての恒等式となるように、定数$a,b,c$の値を求めよ。
(1)
$3x^2+8x+6=a(x+1)^2+b(x+1)+c$
(2)
$\displaystyle \frac{3}{(x-1)(2x+1)}=\displaystyle \frac{a}{x-1}+\displaystyle \frac{b}{2x-1}$
この動画を見る
次の式が$x$についての恒等式となるように、定数$a,b,c$の値を求めよ。
(1)
$3x^2+8x+6=a(x+1)^2+b(x+1)+c$
(2)
$\displaystyle \frac{3}{(x-1)(2x+1)}=\displaystyle \frac{a}{x-1}+\displaystyle \frac{b}{2x-1}$
うまい方法

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3+2x^2+3x+4=0$の3つの解を$ \alpha,\beta,\delta $とする.
$(\alpha^4-1)(\beta^4-1)(\delta^4-1)$の値を求めよ.
この動画を見る
$ x^3+2x^2+3x+4=0$の3つの解を$ \alpha,\beta,\delta $とする.
$(\alpha^4-1)(\beta^4-1)(\delta^4-1)$の値を求めよ.
【数Ⅱ】軌跡の基本 アポロニウスの円【書き方と意味を理解しよう】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 点A(-1,0),点B(2,0)からの距離の比が2:1である点Pの軌跡を求めよ.$
この動画を見る
$ 点A(-1,0),点B(2,0)からの距離の比が2:1である点Pの軌跡を求めよ.$
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 3^{3^{4}}$ VS $ 4^{4^{3}}$
どちらが大きいか求めよ.
*$ 3^5=243,2^8=256$
$ ell= \displaystyle \lim_{n \to \infty} \left(1+\dfrac{1}{n}\right) \lt 3 $
この動画を見る
$ 3^{3^{4}}$ VS $ 4^{4^{3}}$
どちらが大きいか求めよ.
*$ 3^5=243,2^8=256$
$ ell= \displaystyle \lim_{n \to \infty} \left(1+\dfrac{1}{n}\right) \lt 3 $
福田の入試問題解説〜北海道大学2022年文系第1問〜剰余定理と高次不等式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
この動画を見る
kを実数の定数とし、
$f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-k+1$
とする。
(1)$f(k-1)$の値を求めよ。
(2)$|k|\lt 2$のとき、不等式$f(x) \geqq 0$を解け。
2022北海道大学文系過去問
ただの対数方程式

ただの対数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\log_2 x+\log_3 x=1$
この動画を見る
これを解け.
$\log_2 x+\log_3 x=1$
