 数学的帰納法
数学的帰納法
 数学的帰納法
数学的帰納法
【数B】【数列】nは自然数とする。2数x, yの和、積がともに整数ならば、xn+ynは整数であることを、数学的帰納法によって証明せよ。

単元:
#数列#数学的帰納法#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$ は自然数とする。2 数 $x$、$y$ の和、積が
ともに整数ならば、$x^n+y^n$ は整数であることを、
数学的帰納法によって証明せよ。
この動画を見る
$n$ は自然数とする。2 数 $x$、$y$ の和、積が
ともに整数ならば、$x^n+y^n$ は整数であることを、
数学的帰納法によって証明せよ。
福田の数学〜立教大学2025理学部第4問〜整式がある数の倍数であることの証明

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$n$を$2$以上の自然数とする。次の問いに答えよ。
(1)$n^3-n$は$6$のばいすうであることを示せ。
(2)$n^4+2n^3-n^2-2n$は$24$の倍数であることを示せ。
(3)$n$に関する数学的帰納法を用いて、
$n^5+4n$は$5$の倍数であることを示せ。
(4)$n^9+2n^8-n^7-2n^6+4n^5+8n^4-4n^3-8n^2$は
$120$の倍数であることを示せ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{4}$
$n$を$2$以上の自然数とする。次の問いに答えよ。
(1)$n^3-n$は$6$のばいすうであることを示せ。
(2)$n^4+2n^3-n^2-2n$は$24$の倍数であることを示せ。
(3)$n$に関する数学的帰納法を用いて、
$n^5+4n$は$5$の倍数であることを示せ。
(4)$n^9+2n^8-n^7-2n^6+4n^5+8n^4-4n^3-8n^2$は
$120$の倍数であることを示せ。
$2025$年立教大学理学部過去問題
福田の数学〜慶應義塾大学看護医療学部2025第2問(3)〜数学的帰納法

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(3)自然数$n$に対して、
$3^n-2n-1$が
$4$の倍数であることの数学的帰納法を
用いた証明を記述しなさい。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(3)自然数$n$に対して、
$3^n-2n-1$が
$4$の倍数であることの数学的帰納法を
用いた証明を記述しなさい。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学383〜関数方程式

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
この動画を見る
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
福田のおもしろ数学353〜1が連続3^n個並ぶ数は3^nで割り切れることの証明
単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
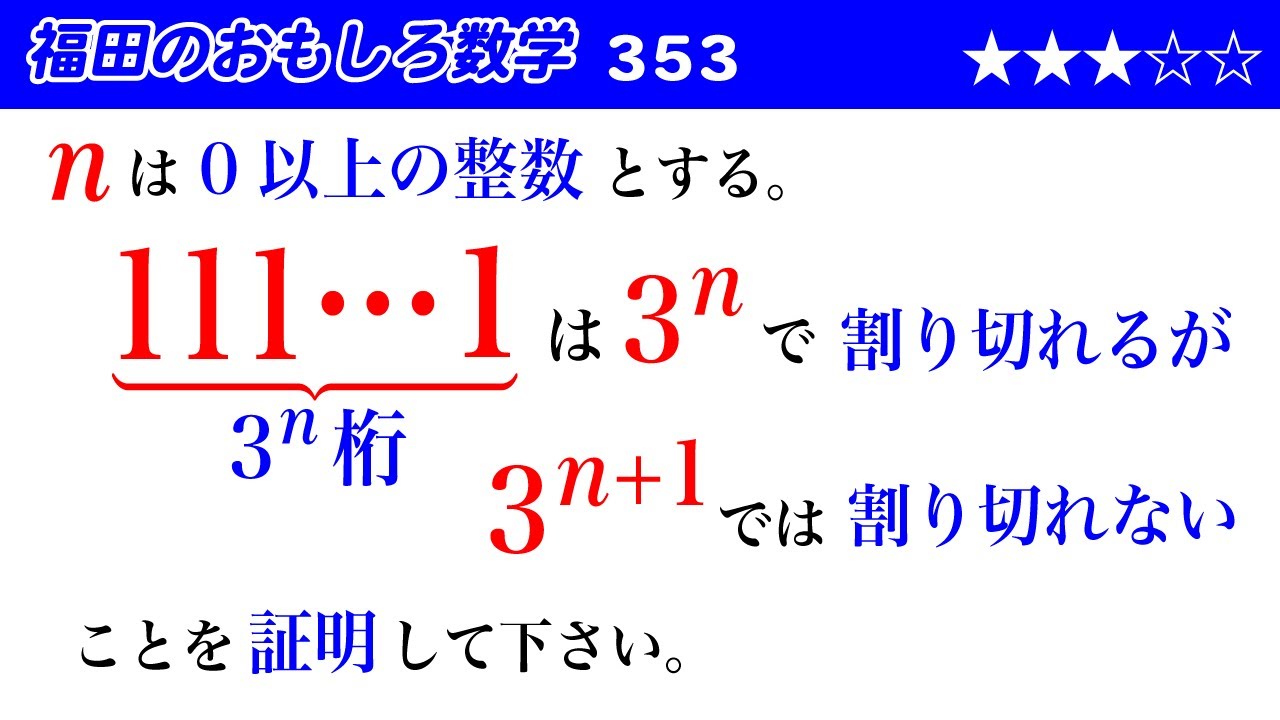
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
この動画を見る
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
福田のおもしろ数学323〜小数部分の和を不等式で評価する

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
この動画を見る
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
福田のおもしろ数学316〜x^n+x^{-n}が整数である証明と倍数

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
この動画を見る
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
福田のおもしろ数学309〜自然数から自然数への関数f(n)に関する関数方程式

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$$自然数を自然数へ写す関数f(n)が次を満たす。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow \frac{1}{f(a)}+\frac{1}{f(b)}=\frac{1}{f(c)}$$
$$このような関数f(n)をすべて求めて下さい。$$
この動画を見る
$$自然数を自然数へ写す関数f(n)が次を満たす。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow \frac{1}{f(a)}+\frac{1}{f(b)}=\frac{1}{f(c)}$$
$$このような関数f(n)をすべて求めて下さい。$$
福田のおもしろ数学267〜複雑な漸化式と特殊な数学的帰納法

単元:
#数列#漸化式#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_0,a_1,a_2,\cdots$が$a_1=1,a_{m+n}=\dfrac12(a_{2m}+a_{2n})~~(m\geqq n)$で定義されている。$a_{2024}$を求めよ。($m,n$は負では無い整数)
この動画を見る
$a_0,a_1,a_2,\cdots$が$a_1=1,a_{m+n}=\dfrac12(a_{2m}+a_{2n})~~(m\geqq n)$で定義されている。$a_{2024}$を求めよ。($m,n$は負では無い整数)
大学入試問題#923「帰納法で解いても良いのかな」

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
この動画を見る
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
福田のおもしろ数学142〜チェビシェフの多項式に関する証明

単元:
#数Ⅱ#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$n$を正の整数とする。$\cos n\theta$は$\cos\theta$の$n$次式で表されることを証明してください。
この動画を見る
$n$を正の整数とする。$\cos n\theta$は$\cos\theta$の$n$次式で表されることを証明してください。
福田のおもしろ数学100〜帰納的に考える方法〜階段の登り方

共テ数学90%取る勉強法

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#式と証明#複素数と方程式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#指数関数#対数関数#平均変化率・極限・導関数#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト数学90%取る勉強法説明動画です
この動画を見る
共通テスト数学90%取る勉強法説明動画です
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜上智大学2023年理工学部第3問〜対数関数の積分と数学的帰納法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
この動画を見る
$\Large\boxed{3}$ $e$を自然定数の底とする。自然数$n$に対して、
$S_n$=$\displaystyle\int_1^e(\log x)^n dx$
とする。
(1)$S_1$の値を求めよ。
(2)すべての自然数$n$に対して、
$S_n$=$a_n e$+$b_n$, ただし$a_n$, $b_n$はいずれも整数
と表されることを証明せよ。
9月からでも間に合うチート級参考書<数学編>

単元:
#数列#数学的帰納法#その他#数学(高校生)#数B#参考書紹介
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学編】9月からでも間に合う参考書紹介動画です
この動画を見る
【数学編】9月からでも間に合う参考書紹介動画です
大阪市立大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
20216大阪市立大学過去問題
x,y整数 n自然数
$x^2+y^2$が$3^{2n-1}$の倍数ならx,yともに$3^n$の倍数であることを示せ
①n=1のとき
②n=2のとき
③すべての自然数n
この動画を見る
20216大阪市立大学過去問題
x,y整数 n自然数
$x^2+y^2$が$3^{2n-1}$の倍数ならx,yともに$3^n$の倍数であることを示せ
①n=1のとき
②n=2のとき
③すべての自然数n
福田の数学〜立教大学2023年理学部第4問〜数学的帰納法とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#数学的帰納法#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
この動画を見る
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
大学入試問題#562「証明問題じゃなきゃ解けるのか?」 東京帝国大学1937 #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$:正の整数
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{\sin(2n-1)x}{\sin\ x}\ dx=\pi$を示せ
出典:1937年東京帝国大学 入試問題
この動画を見る
$n$:正の整数
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{\sin(2n-1)x}{\sin\ x}\ dx=\pi$を示せ
出典:1937年東京帝国大学 入試問題
整数問題

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
この動画を見る
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
福田の数学〜慶應義塾大学2023年看護医療学部第2問(3)〜推定して数学的帰納法

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (3) 次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1$=1, $a_{n+1}$=$\sqrt{a_n^2+1}$ ($n$=1,2,3,...)
(i)$a_2$=$\boxed{\ \ シ\ \ }$, $a_3$=$\boxed{\ \ ス\ \ }$であり、一般項$a_n$を推定すると$a_n$=$\boxed{\ \ セ\ \ }$である。
(ii)一般項$a_n$が$a_n$=$\boxed{\ \ セ\ \ }$であることの数学的帰納法による証明を述べよ。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (3) 次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1$=1, $a_{n+1}$=$\sqrt{a_n^2+1}$ ($n$=1,2,3,...)
(i)$a_2$=$\boxed{\ \ シ\ \ }$, $a_3$=$\boxed{\ \ ス\ \ }$であり、一般項$a_n$を推定すると$a_n$=$\boxed{\ \ セ\ \ }$である。
(ii)一般項$a_n$が$a_n$=$\boxed{\ \ セ\ \ }$であることの数学的帰納法による証明を述べよ。
2023慶應義塾大学看護医療学部過去問
福田の数学〜早稲田大学2023年理工学部第2問〜玉を取り出す確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 赤玉と黒玉が入っている袋の中から無作為に玉を1つ取り出し、取り出した玉を袋に戻した上で、取り出した玉と同じ色の玉をもう1つ袋に入れる操作を繰り返す。以下の問いに答えよ。
(1)初めに袋の中に赤玉が1個、黒玉が1個入っているとする。n回の操作を行ったとき、赤玉をちょうどk回取り出す確率を$P_n(k)$(k=0,1,...,n)とする。
$P_1(k)$と$P_2(k)$を求め、さらに$P_n(k)$を求めよ。
(2)初めに袋の中に赤玉がr個、黒玉がb個(r≧1, b≧1)入っているとする。n回の操作を行ったとき、k回目に赤玉が、それ以外ではすべて黒玉が取り出される確率$Q_n(k)$(k=1,2,..., n)とする。$Q_n(k)$はkによらないことを示せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{2}$ 赤玉と黒玉が入っている袋の中から無作為に玉を1つ取り出し、取り出した玉を袋に戻した上で、取り出した玉と同じ色の玉をもう1つ袋に入れる操作を繰り返す。以下の問いに答えよ。
(1)初めに袋の中に赤玉が1個、黒玉が1個入っているとする。n回の操作を行ったとき、赤玉をちょうどk回取り出す確率を$P_n(k)$(k=0,1,...,n)とする。
$P_1(k)$と$P_2(k)$を求め、さらに$P_n(k)$を求めよ。
(2)初めに袋の中に赤玉がr個、黒玉がb個(r≧1, b≧1)入っているとする。n回の操作を行ったとき、k回目に赤玉が、それ以外ではすべて黒玉が取り出される確率$Q_n(k)$(k=1,2,..., n)とする。$Q_n(k)$はkによらないことを示せ。
2023早稲田大学理工学部過去問
福田の数学〜早稲田大学2023年理工学部第1問〜整式の割り算の商に関する論証

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを自然数として、整式$(3x+2)^n$を$x^2$+$x$+1で割った余りを$a_nx$+$b_n$とおく。
(1)$a_{n+1}$と$b_{n+1}$を、それぞれ$a_n$と$b_n$を用いて表せ。
(2)全てのnに対して、$a_n$と$b_n$は7で割り切れないことを示せ。
(3)$a_n$と$b_n$を$a_{n+1}$と$b_{n+1}$で表し、全てのnに対して、2つの整数$a_n$と$b_n$は互いに素であることを示せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{1}$ nを自然数として、整式$(3x+2)^n$を$x^2$+$x$+1で割った余りを$a_nx$+$b_n$とおく。
(1)$a_{n+1}$と$b_{n+1}$を、それぞれ$a_n$と$b_n$を用いて表せ。
(2)全てのnに対して、$a_n$と$b_n$は7で割り切れないことを示せ。
(3)$a_n$と$b_n$を$a_{n+1}$と$b_{n+1}$で表し、全てのnに対して、2つの整数$a_n$と$b_n$は互いに素であることを示せ。
2023早稲田大学理工学部過去問
大学入試問題#463「ええ問題や~~」 信州大学 理・医 (2016) #積分の応用

単元:
#大学入試過去問(数学)#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典:2016年信州大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典:2016年信州大学医学部 入試問題
東大 レピュニット数

単元:
#数A#大学入試過去問(数学)#整数の性質#数列#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\overbrace{ 1111 + \cdots +11}^{3^n桁}$は$3^n$で割り切れるが
$3^{n+1}$では割り切れないことを示せ.
東大過去問
この動画を見る
$\overbrace{ 1111 + \cdots +11}^{3^n桁}$は$3^n$で割り切れるが
$3^{n+1}$では割り切れないことを示せ.
東大過去問
福田の1.5倍速演習〜合格する重要問題035〜東京大学2017年度理系第4問〜数列の帰納的定義と最大公約数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
この動画を見る
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
福田の1.5倍速演習〜合格する重要問題016〜京都大学2016年度理系数学第2問〜素数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学的帰納法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
この動画を見る
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
あみだくじってなんで重ならない?

単元:
#数列#数学的帰納法#微分とその応用#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
あみだくじは、なぜ人数や線を増やしてもかぶらないんですか?
この動画を見る
下記質問の解説動画です
あみだくじは、なぜ人数や線を増やしてもかぶらないんですか?
福田の数学〜早稲田大学2022年商学部第1問(1)〜漸化式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a_2=4$
$(\textrm{ii})a_{n+2}=a_n^{\log_2a_{n+1}} (n=1,2,3,\ldots)$
このとき、$\log_2(\log_2a_{10})=\boxed{\ \ ア\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(1)数列$\left\{a_n\right\}$が次の条件を満たしている。
$(\textrm{i})a_1=a_2=4$
$(\textrm{ii})a_{n+2}=a_n^{\log_2a_{n+1}} (n=1,2,3,\ldots)$
このとき、$\log_2(\log_2a_{10})=\boxed{\ \ ア\ \ }$である。
2022早稲田大学商学部過去問
大学入試問題#237 岡山県立大学(2020) #数学的帰納法

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$:自然数
2020年岡山県立大学 入試問題
この動画を見る
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$:自然数
2020年岡山県立大学 入試問題
