 数列
数列
 数列
数列
東大 レピュニット数

単元:
#数A#大学入試過去問(数学)#整数の性質#数列#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\overbrace{ 1111 + \cdots +11}^{3^n桁}$は$3^n$で割り切れるが
$3^{n+1}$では割り切れないことを示せ.
東大過去問
この動画を見る
$\overbrace{ 1111 + \cdots +11}^{3^n桁}$は$3^n$で割り切れるが
$3^{n+1}$では割り切れないことを示せ.
東大過去問
近畿大(医)やっぱり出た2023年問題

単元:
#数A#大学入試過去問(数学)#整数の性質#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
この動画を見る
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
階乗に関する方程式
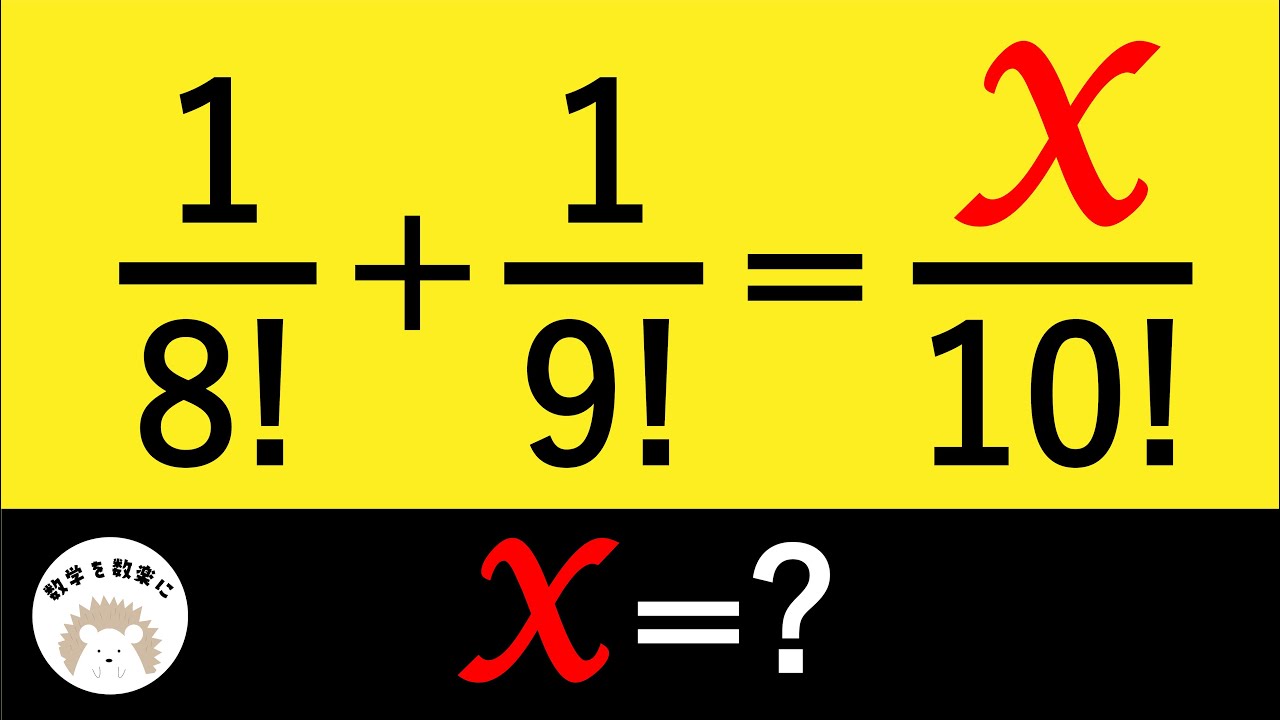
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{8!} + \frac{1}{9!} = \frac{x}{10!}$
x=?
この動画を見る
$\frac{1}{8!} + \frac{1}{9!} = \frac{x}{10!}$
x=?
福田の1.5倍速演習〜合格する重要問題072〜上智大学2019年度理工学部第3問〜ガウス記号で定義された数列

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
この動画を見る
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題070〜筑波大学2017年度理系第5問〜格子点の個数とガウス記号と区分求積

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ xy平面において、x座標とy座標がともに整数である点を格子点という。また、実数aに対して、a以下の最大の整数を[a]で表す。記号[ ]をガウス記号という。
以下の問いではNを自然数とする。
(1) nを0 $\leqq$ n $\leqq$ Nを満たす整数とする。点(n, 0)と点(n, N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$)を結ぶ線分上にある格子点の個数をガウス記号を用いて表せ。
(2) 直線y=xと、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をA(N)とおく。このときA(N)を求めよ。
(3) 曲線y=N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$(0 $\leqq$ x $\leqq$ N)と、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をB(N)とおく。(2)のA(N)に対して$\displaystyle\lim_{N \to \infty}\frac{B(N)}{A(N)}$を求めよ。
2017筑波大学理系過去問
この動画を見る
$\Large{\boxed{5}}$ xy平面において、x座標とy座標がともに整数である点を格子点という。また、実数aに対して、a以下の最大の整数を[a]で表す。記号[ ]をガウス記号という。
以下の問いではNを自然数とする。
(1) nを0 $\leqq$ n $\leqq$ Nを満たす整数とする。点(n, 0)と点(n, N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$)を結ぶ線分上にある格子点の個数をガウス記号を用いて表せ。
(2) 直線y=xと、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をA(N)とおく。このときA(N)を求めよ。
(3) 曲線y=N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$(0 $\leqq$ x $\leqq$ N)と、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をB(N)とおく。(2)のA(N)に対して$\displaystyle\lim_{N \to \infty}\frac{B(N)}{A(N)}$を求めよ。
2017筑波大学理系過去問
【数列】超基本的な問題です!解けますか?【甲南大学】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
9を分母とする正の既約分数で,100より小さいものの総和を求めよ。
甲南大過去問
この動画を見る
9を分母とする正の既約分数で,100より小さいものの総和を求めよ。
甲南大過去問
福田の1.5倍速演習〜合格する重要問題068〜千葉大学2017年度理系第11問〜部分和で定義された数列の極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#千葉大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{11}}$ 数列$\left\{a_n\right\}$を次の条件によって定める。
$a_1=2$, $a_{n+1}=1+\frac{1}{\displaystyle1-\sum_{k=1}^n\frac{1}{a_k}}$ (n=1,2,3,$\cdots$)
(1) $a_5$を求めよ。
(2) $a_{n+1}$を$a_n$の式で表せ。
(3) 無限級数$\displaystyle\sum_{k=1}^{\infty}\frac{1}{a_k}$が収束することを示し、その和を求めよ。
2017千葉大学理系過去問
この動画を見る
$\Large{\boxed{11}}$ 数列$\left\{a_n\right\}$を次の条件によって定める。
$a_1=2$, $a_{n+1}=1+\frac{1}{\displaystyle1-\sum_{k=1}^n\frac{1}{a_k}}$ (n=1,2,3,$\cdots$)
(1) $a_5$を求めよ。
(2) $a_{n+1}$を$a_n$の式で表せ。
(3) 無限級数$\displaystyle\sum_{k=1}^{\infty}\frac{1}{a_k}$が収束することを示し、その和を求めよ。
2017千葉大学理系過去問
福田の1.5倍速演習〜合格する重要問題066〜九州大学2017年度理系第3問〜等差数列の7の倍数になる項の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
この動画を見る
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
福田の1.5倍速演習〜合格する重要問題065〜中央大学2019年度理工学部第3問〜反復試行と確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
この動画を見る
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
無限等比級数

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +\frac{1}{16} +\frac{1}{32} + \cdots =?$
この動画を見る
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +\frac{1}{16} +\frac{1}{32} + \cdots =?$
福田の数学〜北里大学2021年医学部第2問〜条件が複雑な重複順列

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ $n$ を正の整数とし、1,2,3,4,5,6の6個の数字から同じ数字を繰り返し用いることを許して$n$桁の整数をつくる。このような整数のうち、1が奇数個用いられるものの総数を$A_n$、それ以外のものの総数を$B_n$とする。
また、1か6がいずれも奇数個用いられるものの総数を$C_n$とする。次の問いに答えよ。
(1)$A_4$を求めよ。
(2)正の整数$n$に対して、$A_{n+1}$を$A_n$と$B_n$を用いて表せ。
(3)正の整数$n$に対して、$A_n$と$B_n$を求めよ。
(4)$p$を定数とする。$X_1=p$,$X_{n+1}=2X_n+6^n$($n$=1,2,3,...)で定められる
数列を$\left\{X_n\right\}$とする。正の整数$n$に対して、$X_n$を$n$と$p$を用いて表せ。
(5)正の整数$n$に対して、$C_n$を求めよ。
2021北里大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ $n$ を正の整数とし、1,2,3,4,5,6の6個の数字から同じ数字を繰り返し用いることを許して$n$桁の整数をつくる。このような整数のうち、1が奇数個用いられるものの総数を$A_n$、それ以外のものの総数を$B_n$とする。
また、1か6がいずれも奇数個用いられるものの総数を$C_n$とする。次の問いに答えよ。
(1)$A_4$を求めよ。
(2)正の整数$n$に対して、$A_{n+1}$を$A_n$と$B_n$を用いて表せ。
(3)正の整数$n$に対して、$A_n$と$B_n$を求めよ。
(4)$p$を定数とする。$X_1=p$,$X_{n+1}=2X_n+6^n$($n$=1,2,3,...)で定められる
数列を$\left\{X_n\right\}$とする。正の整数$n$に対して、$X_n$を$n$と$p$を用いて表せ。
(5)正の整数$n$に対して、$C_n$を求めよ。
2021北里大学医学部過去問
福田の1.5倍速演習〜合格する重要問題043〜北海道大学2017年度文系第3問〜確率漸化式の定番問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師:
福田次郎
問題文全文(内容文):
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
この動画を見る
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
福田の1.5倍速演習〜合格する重要問題039〜早稲田大学2019年度理工学部第2問〜正n角形の周の長さと極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
nは3以上の自然数とする。面積1の正n角形$P_n$を考え、その周の
長さを$L_n$とする。次の問いに答えよ。
(1)$(L_n)^2$を求めよ。
(2)$\lim_{n \to \infty}L_n$を求めよ。
(3)$n \lt k$ならば$(L_n)^2 \gt (L_k)^2$となることを示せ。
2019早稲田大学理工学部過去問
この動画を見る
nは3以上の自然数とする。面積1の正n角形$P_n$を考え、その周の
長さを$L_n$とする。次の問いに答えよ。
(1)$(L_n)^2$を求めよ。
(2)$\lim_{n \to \infty}L_n$を求めよ。
(3)$n \lt k$ならば$(L_n)^2 \gt (L_k)^2$となることを示せ。
2019早稲田大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題035〜東京大学2017年度理系第4問〜数列の帰納的定義と最大公約数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
この動画を見る
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
2023にしたかったのだけど‥‥

【高校数学】数列の和と一般項の例題 3-11【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
初項から第n項までの和SnがSn = n² + 3nで表される数列{a_n}の一般項を求めよ。
この動画を見る
初項から第n項までの和SnがSn = n² + 3nで表される数列{a_n}の一般項を求めよ。
福田の1.5倍速演習〜合格する重要問題023〜名古屋大学2016年度理系数学第3問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数B
指導講師:
福田次郎
問題文全文(内容文):
玉が2個ずつ入った2つの袋A,Bがあるとき、袋Bから玉を1個取り出して
袋Aに入れ、次に袋Aから玉を1個取り出して袋Bに入れる。という操作を
1回の操作と数えることにする。Aに赤玉が2個、Bに白玉が2個入った状態から
始め、この操作をn回繰り返した後に袋Bに入っている赤玉の個数がk個で
ある確率を$P_n(k)(n=1,2,3,\cdots)$とする。このとき、次の問いに答えよ。
(1)$k=0,1,2$に対する$P_1(k)$を求めよ。
(2)$k=0,1,2$に対する$P_n(k)$を求めよ。
2016名古屋大学理系過去問
この動画を見る
玉が2個ずつ入った2つの袋A,Bがあるとき、袋Bから玉を1個取り出して
袋Aに入れ、次に袋Aから玉を1個取り出して袋Bに入れる。という操作を
1回の操作と数えることにする。Aに赤玉が2個、Bに白玉が2個入った状態から
始め、この操作をn回繰り返した後に袋Bに入っている赤玉の個数がk個で
ある確率を$P_n(k)(n=1,2,3,\cdots)$とする。このとき、次の問いに答えよ。
(1)$k=0,1,2$に対する$P_1(k)$を求めよ。
(2)$k=0,1,2$に対する$P_n(k)$を求めよ。
2016名古屋大学理系過去問
福田の1.5倍速演習〜合格する重要問題016〜京都大学2016年度理系数学第2問〜素数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学的帰納法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
この動画を見る
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
【高校数学】数列の和と一般項~理解して覚えようね~ 3-10【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
数列の和と一般項の関係について解説しています。
この動画を見る
数列の和と一般項の関係について解説しています。
福田の1.5倍速演習〜合格する重要問題003〜北海道大学2015年文系数学第4問〜隣り合う順列、隣り合わない順列

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
この動画を見る
ジョーカーを除く1組52枚のトランプのカードを1列に並べる思考を考える。
(1)番号7のカードが4枚連続して並ぶ確率を求めよ。
(2)番号7のカードが2枚ずつ隣り合い、4枚連続しては並ばない確率を求めよ。
8人の人が一列に並ぶとき、
(1)A,B,Cの3人が連続して並ぶ場合の数を求めよ。
(2)A,B,Cの3人が隣りあわないように並ぶ場合の数を求めよ。
2015北海道大学文系過去問
福田の数学〜北里大学2022年医学部第3問〜確率と漸化式の融合問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
この動画を見る
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
あみだくじってなんで重ならない?

単元:
#数列#数学的帰納法#微分とその応用#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
あみだくじは、なぜ人数や線を増やしてもかぶらないんですか?
この動画を見る
下記質問の解説動画です
あみだくじは、なぜ人数や線を増やしてもかぶらないんですか?
見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \underbrace{777・・・・・・77^7}_{101桁}$を18で割ったあまりを求めよ.
この動画を見る
$ \underbrace{777・・・・・・77^7}_{101桁}$を18で割ったあまりを求めよ.
福田の数学〜上智大学2022年理工学部第3問〜複素数平面上の点列と三角形の相似

単元:
#大学入試過去問(数学)#複素数平面#相似な図形#数列#漸化式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
この動画を見る
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
漸化式・対数の利用の融合問題 福井大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
この動画を見る
$ a_1=1,a_{n+1}=\dfrac{a_n}{a_n+3},a_{11}$は小数点以下0でない数が初めて表れるのは小数第何位?
福井大過去問
高知大(医)3項間漸化式

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=1,a_2=5,a_{n+2}=4a_{n+1}-3a_n-4$
の一般項$a_n$を求めよ.
高知大(医)過去問
この動画を見る
$ a_1=1,a_2=5,a_{n+2}=4a_{n+1}-3a_n-4$
の一般項$a_n$を求めよ.
高知大(医)過去問
東京女子大 漸化式・数列の最大値

単元:
#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1$は7であり,$n^2a_{n+1}-(n+1)^2a_n=-n^2(n+1)^2$である.
(1)$a_n$の一般項を求めよ.
(2)$a_n$の最大値を求めよ.
東京女子大過去問
この動画を見る
$ a_1$は7であり,$n^2a_{n+1}-(n+1)^2a_n=-n^2(n+1)^2$である.
(1)$a_n$の一般項を求めよ.
(2)$a_n$の最大値を求めよ.
東京女子大過去問
室蘭工業大 漸化式基本

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=2,a_{n+1}=\dfrac{1}{2}a_n+\dfrac{4n+2^n}{2^{n+1}}$である.
$a_n\lt a_{n+1}$を満たす最大の自然数$n$を求めよ.
室蘭工業大過去問
この動画を見る
$ a_1=2,a_{n+1}=\dfrac{1}{2}a_n+\dfrac{4n+2^n}{2^{n+1}}$である.
$a_n\lt a_{n+1}$を満たす最大の自然数$n$を求めよ.
室蘭工業大過去問
記号は大学数学でも頑張れば中学生でもできる
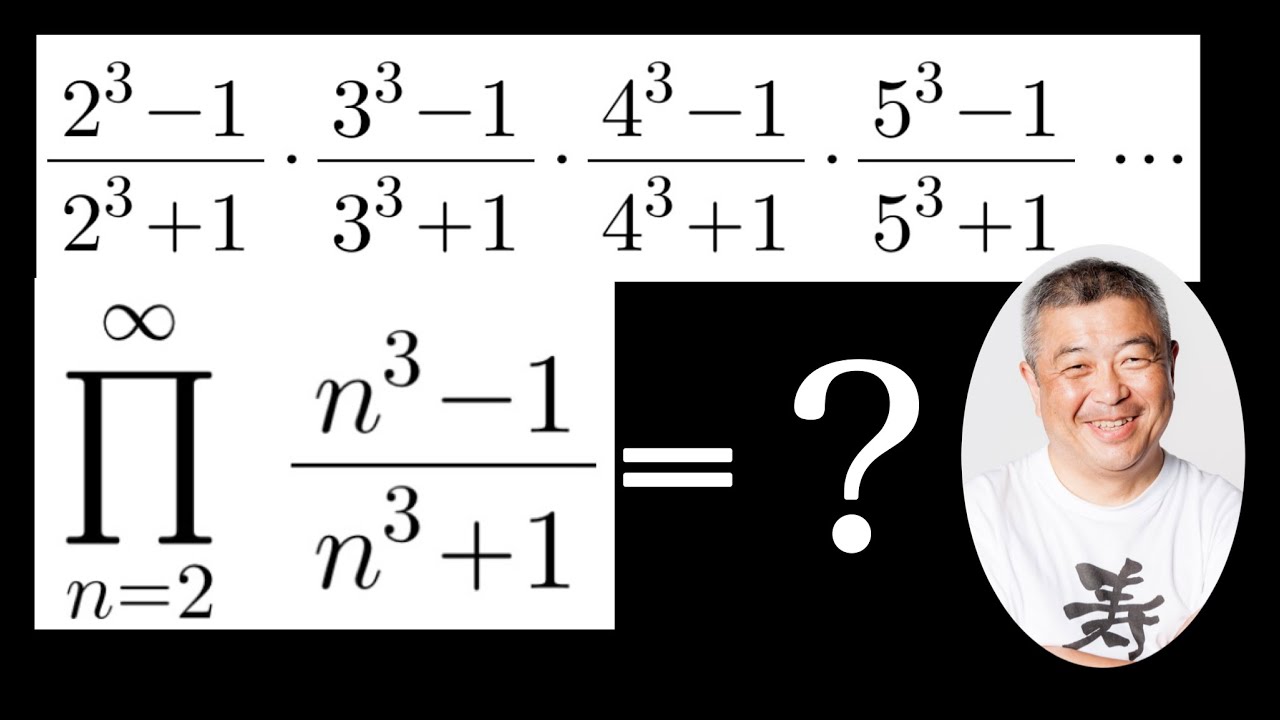
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{2^3-1}{2^3+1}・\dfrac{3^3-1}{3^3+1}・\dfrac{4^3-1}{4^3+1}・\dfrac{5^3-1}{5^3+1}…$
$\displaystyle \prod_{n=2}^{\infty} \dfrac{n^3-1}{n^3+1}=?$
これを解け.
この動画を見る
$\dfrac{2^3-1}{2^3+1}・\dfrac{3^3-1}{3^3+1}・\dfrac{4^3-1}{4^3+1}・\dfrac{5^3-1}{5^3+1}…$
$\displaystyle \prod_{n=2}^{\infty} \dfrac{n^3-1}{n^3+1}=?$
これを解け.
福田の数学〜立教大学2022年経済学部第1問(5)〜群数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
この動画を見る
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
