 数列
数列
 数列
数列
大学入試問題#12 獨協大学(2021) 数列
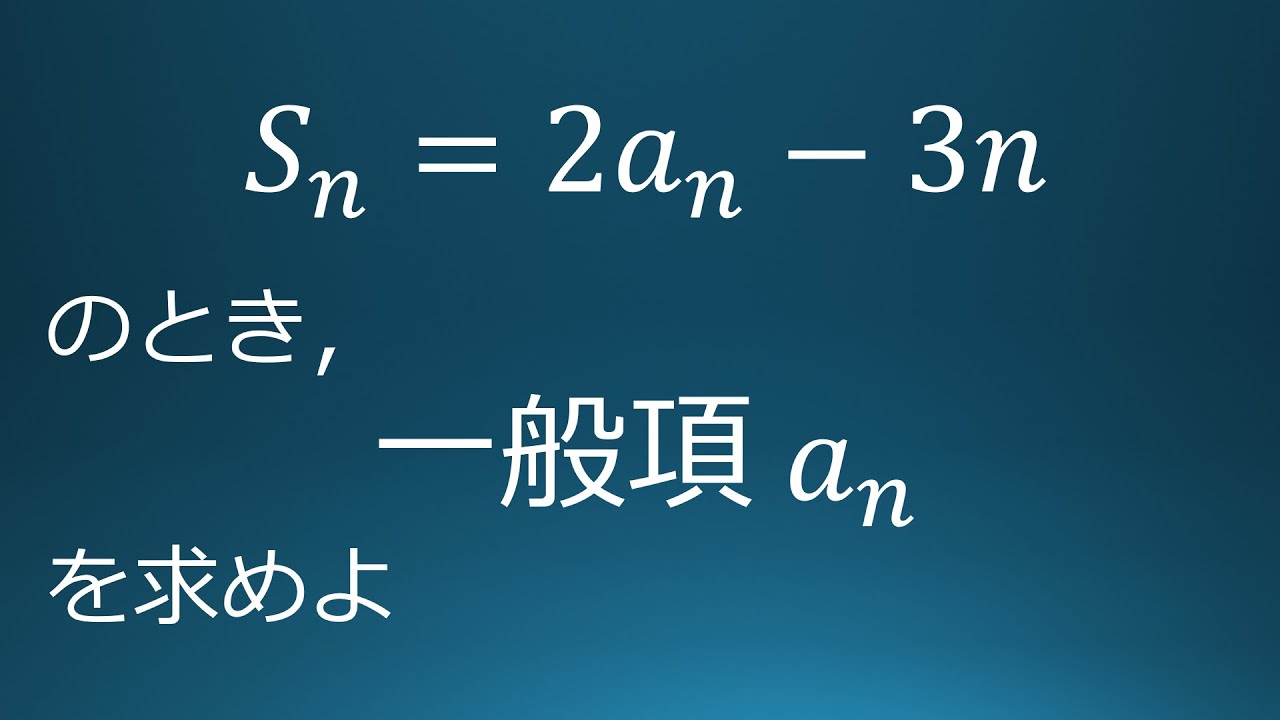
福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(1)〜連立型の漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)数列$\left\{a_n\right\},\ \left\{b_n\right\}$について次の条件が与えられている。
$\left\{
\begin{array}{1}
a_{n+1}=7a_n-10b_n\\
b_{n+1}=2a_n-2b_n
\end{array}
\right. (n=1,2,3,\ldots)$
ただし、$a_1=11,\ b_1=4$とする。このとき、
$\left\{
\begin{array}{1}
c_n=a_n-2b_n \\
d_n=2a_n-5b_n
\end{array}
\right. (n=1,2,3,\ldots)$
とおくと、$c_n=\boxed{\ \ ア\ \ }^n, d_n=\boxed{\ \ イ\ \ }^n$であり、これより$\left\{a_n\right\},\ \left\{b_n\right\}$
の一般項は
$\left\{
\begin{array}{1}
a_n=\boxed{\ \ ウ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ エ\ \ }・\boxed{\ \ イ\ \ }^n\\
b_n=\boxed{\ \ オ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ イ\ \ }^n \\
\end{array}
\right.$
である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{1}}$(1)数列$\left\{a_n\right\},\ \left\{b_n\right\}$について次の条件が与えられている。
$\left\{
\begin{array}{1}
a_{n+1}=7a_n-10b_n\\
b_{n+1}=2a_n-2b_n
\end{array}
\right. (n=1,2,3,\ldots)$
ただし、$a_1=11,\ b_1=4$とする。このとき、
$\left\{
\begin{array}{1}
c_n=a_n-2b_n \\
d_n=2a_n-5b_n
\end{array}
\right. (n=1,2,3,\ldots)$
とおくと、$c_n=\boxed{\ \ ア\ \ }^n, d_n=\boxed{\ \ イ\ \ }^n$であり、これより$\left\{a_n\right\},\ \left\{b_n\right\}$
の一般項は
$\left\{
\begin{array}{1}
a_n=\boxed{\ \ ウ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ エ\ \ }・\boxed{\ \ イ\ \ }^n\\
b_n=\boxed{\ \ オ\ \ }・\boxed{\ \ ア\ \ }^n-\boxed{\ \ イ\ \ }^n \\
\end{array}
\right.$
である。
2021明治大学全統過去問
【高校数学】等比中項の証明~理解して暗記しよう~ 3-6【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【数学B】等比中項の証明についての説明動画です
この動画を見る
【数学B】等比中項の証明についての説明動画です
神様の順列で瞬殺

単元:
#数A#場合の数と確率#確率#数列#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
52枚のトランプから1枚引いて見ないで伏せる.
残り51枚から3枚引いたら全部♡だった.
伏せた1枚が♡である確率を求めよ.
この動画を見る
52枚のトランプから1枚引いて見ないで伏せる.
残り51枚から3枚引いたら全部♡だった.
伏せた1枚が♡である確率を求めよ.
群数列 近江高校(改)

単元:
#数学(中学生)#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
群数列
$\frac{1}{2} \quad \frac{2}{3} \quad \frac{1}{3} \quad \frac{3}{4} \quad \frac{2}{4} \quad \frac{1}{4} \quad \frac{4}{5} \quad \frac{3}{5} $
$① \quad ② \quad ③ \quad ④ \quad ⑤ \quad ⑥ \quad ⑦ \quad ⑧ $
近江高等学校(改)
この動画を見る
群数列
$\frac{1}{2} \quad \frac{2}{3} \quad \frac{1}{3} \quad \frac{3}{4} \quad \frac{2}{4} \quad \frac{1}{4} \quad \frac{4}{5} \quad \frac{3}{5} $
$① \quad ② \quad ③ \quad ④ \quad ⑤ \quad ⑥ \quad ⑦ \quad ⑧ $
近江高等学校(改)
【数学B/テスト対策】階差数列(一般項)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の数列の一般項$a_n$を求めよ。
(1)$2,5,10,17,26,37…$
(2)$3,4,6,10,18,…$
この動画を見る
次の数列の一般項$a_n$を求めよ。
(1)$2,5,10,17,26,37…$
(2)$3,4,6,10,18,…$
福田の数学〜中央大学2021年経済学部第1問(5)〜漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)次の条件によって定められる数列$\left\{a_n\right\}$の一般項を求めよ。
$a_1=-1, a_{n+1}=a_n+2・3^{n-1} (n=1,2,3,\ldots)$
2021中央大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(5)次の条件によって定められる数列$\left\{a_n\right\}$の一般項を求めよ。
$a_1=-1, a_{n+1}=a_n+2・3^{n-1} (n=1,2,3,\ldots)$
2021中央大学経済学部過去問
【数B】高2生必見!! 2019年度8月 第2回 K塾高2模試 大問6_数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列{$a_n$}($n=1,2,3,...$)は初項-8、公差4の等差数列であり、数列{$b_n$} ($n=1,2,3,...$)は初項から第n項までの和が$S_n\dfrac{3^n}{2}(n=1,2,3,...)$で与えられ る数列である。
(1)数列{$a_n$}の一般項$a_n$を求めよ。また、数列{$a_n$}の初項から第n項までの 和を求めよ。 (2)$\displaystyle \sum_{k=1}^n (a_k)^2$を求めよ。
(3)数列{$b_n$}の一般項$b_n$を求めよ。 (4)nを3以上の整数とするとき、$\displaystyle \sum_{k=1}^n \vert a_k b_k \vert$を求めよ。
この動画を見る
数列{$a_n$}($n=1,2,3,...$)は初項-8、公差4の等差数列であり、数列{$b_n$} ($n=1,2,3,...$)は初項から第n項までの和が$S_n\dfrac{3^n}{2}(n=1,2,3,...)$で与えられ る数列である。
(1)数列{$a_n$}の一般項$a_n$を求めよ。また、数列{$a_n$}の初項から第n項までの 和を求めよ。 (2)$\displaystyle \sum_{k=1}^n (a_k)^2$を求めよ。
(3)数列{$b_n$}の一般項$b_n$を求めよ。 (4)nを3以上の整数とするとき、$\displaystyle \sum_{k=1}^n \vert a_k b_k \vert$を求めよ。
【数学B/テスト対策】等比数列の一般項と和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
等比数列$-2,6,-18,54,…$について、次の問いに答えよ。
(1)
一般項$a_n$を求めよ。
(2)
初項から第$n$項までの和$S_n$を求めよ。
(3)
初項から第$5$項までの和$S_5$を求めよ。
この動画を見る
等比数列$-2,6,-18,54,…$について、次の問いに答えよ。
(1)
一般項$a_n$を求めよ。
(2)
初項から第$n$項までの和$S_n$を求めよ。
(3)
初項から第$5$項までの和$S_5$を求めよ。
【高校数学】等比数列の一般項の例題演習~公式を使いこなそう~ 3-5.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
次の等比数列の一般項を求めよ。また、第8項を求めよ。
(a)-2,2,-2,2,…
(b)1,-3,9,-27,…
2⃣
第4項が-24、第6項が-96である、等比数列${a_{n}}$の一般項を求めよ。
この動画を見る
1⃣
次の等比数列の一般項を求めよ。また、第8項を求めよ。
(a)-2,2,-2,2,…
(b)1,-3,9,-27,…
2⃣
第4項が-24、第6項が-96である、等比数列${a_{n}}$の一般項を求めよ。
【数学B/テスト対策】等差数列の一般項と和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
等差数列$-2,1,4,7,10…$について、次の問いに答えよ。
(1)一般項$a_n$を求めよ。
(2)第100項$a_{100}$を求めよ。
(3)初項から第$n$項までの和$S_n$を求めよ。
この動画を見る
等差数列$-2,1,4,7,10…$について、次の問いに答えよ。
(1)一般項$a_n$を求めよ。
(2)第100項$a_{100}$を求めよ。
(3)初項から第$n$項までの和$S_n$を求めよ。
福田の数学〜中央大学2021年理工学部第2問〜3項間の漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$コインを繰り返し,連続した3回が順に,表→裏→表,あるいは,裏→表→裏,というパターンが出たときにコイン投げを終了する.$n\geqq 3$に対し,コインをちょうど$n$回投げて終了する確率を$p_n$とする.
以下の手順により$p_n$を求める.コインを$n$回投げて,「まだ終了していないが$n+1$回目に表が出たら終了する」または「まだ終了してないが$n+1$回目に裏が出たら終了する.」という状態にある確率を$r_n$とする.またコインを$n$回投げて「まだ終了しておらず,$n+1$回目に表が出ても裏が出ても終了しない」という状態にある確率を$s_n$とする.
このとき,$r_3=\dfrac{1}{4},s_3=\boxed{ク},r_4=\dfrac{1}{4},s_4=\boxed{ケ}$である.
ここで,$r_{n+4}$と$r_{n},s_n$を用いて表すと,それぞれ$r_{n+1}=\boxed{コ}$,$s_{n+1}=\boxed{サ}$となる.
この動画を見る
$\boxed{2}$コインを繰り返し,連続した3回が順に,表→裏→表,あるいは,裏→表→裏,というパターンが出たときにコイン投げを終了する.$n\geqq 3$に対し,コインをちょうど$n$回投げて終了する確率を$p_n$とする.
以下の手順により$p_n$を求める.コインを$n$回投げて,「まだ終了していないが$n+1$回目に表が出たら終了する」または「まだ終了してないが$n+1$回目に裏が出たら終了する.」という状態にある確率を$r_n$とする.またコインを$n$回投げて「まだ終了しておらず,$n+1$回目に表が出ても裏が出ても終了しない」という状態にある確率を$s_n$とする.
このとき,$r_3=\dfrac{1}{4},s_3=\boxed{ク},r_4=\dfrac{1}{4},s_4=\boxed{ケ}$である.
ここで,$r_{n+4}$と$r_{n},s_n$を用いて表すと,それぞれ$r_{n+1}=\boxed{コ}$,$s_{n+1}=\boxed{サ}$となる.
【高校数学】等比数列の一般項~意味を理解しよう~ 3-5【数学B】

【高校数学】等差数列の和の例題演習・標準 3-4.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
等差数列において、初項から第n項までの和を$S_{n}$とする。
$S_{10}=10,S_{20}=40$のとき、$S_{n}$を求めよ。
2⃣
10から100までの自然数のうち3で割って2余る数の和$S$を求めよ
この動画を見る
1⃣
等差数列において、初項から第n項までの和を$S_{n}$とする。
$S_{10}=10,S_{20}=40$のとき、$S_{n}$を求めよ。
2⃣
10から100までの自然数のうち3で割って2余る数の和$S$を求めよ
【0から理解できる】数学B 等比数列の和 Σ(シグマ)の計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の和を求めよ。
(1)
$\displaystyle \sum_{k=1}^6 2^k$
(2)
$\displaystyle \sum_{k=1}^n (-3)^k$
この動画を見る
次の和を求めよ。
(1)
$\displaystyle \sum_{k=1}^6 2^k$
(2)
$\displaystyle \sum_{k=1}^n (-3)^k$
【高校数学】等差数列の和の例題演習・基礎 3-4.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の等差数列の和を求めよ。
(1)初項100,末項30,項数7
(2)初項50,公差-4,項数n
(3)100,105,110,…,200
この動画を見る
次の等差数列の和を求めよ。
(1)初項100,末項30,項数7
(2)初項50,公差-4,項数n
(3)100,105,110,…,200
福田の数学〜慶應義塾大学2021年看護医療学部第1問(4)〜等比数列となる条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (4)数列$\left\{a_n\right\}$の階差数列を$\left\{b_n\right\}$とする。$\left\{b_n\right\}$が初項2、公比$\frac{1}{3}$の等比数列と
なるとき、$\left\{b_n\right\}$の一般項は$b_n=\boxed{\ \ オ\ \ }$である。また、$\left\{a_n\right\}$も等比数列に
なるならば、$a_1=\boxed{\ \ カ\ \ }$である。このとき$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$ (4)数列$\left\{a_n\right\}$の階差数列を$\left\{b_n\right\}$とする。$\left\{b_n\right\}$が初項2、公比$\frac{1}{3}$の等比数列と
なるとき、$\left\{b_n\right\}$の一般項は$b_n=\boxed{\ \ オ\ \ }$である。また、$\left\{a_n\right\}$も等比数列に
なるならば、$a_1=\boxed{\ \ カ\ \ }$である。このとき$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
【数学B/数列】数列の和 Σ(シグマ)の計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の和を求めよ。
(1)
$\displaystyle \sum_{k=1}^n (3k+5)$
(2)
$\displaystyle \sum_{k=1}^n (k^2+2k+3)$
この動画を見る
次の和を求めよ。
(1)
$\displaystyle \sum_{k=1}^n (3k+5)$
(2)
$\displaystyle \sum_{k=1}^n (k^2+2k+3)$
15和歌山県教員採用試験(数学:4番 帰納法)

単元:
#数列#数学的帰納法#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$n \gets IN$
$3^n$と$5n+2$の大小を比較せよ.
この動画を見る
$\boxed{4}$
$n \gets IN$
$3^n$と$5n+2$の大小を比較せよ.
高専数学 微積II #32(2) 級数の収束条件
単元:
#数Ⅱ#微分法と積分法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{(1+x)^{n-1}}$
が収束するように$x$の範囲を定め,
その和を求めよ.
この動画を見る
$\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{(1+x)^{n-1}}$
が収束するように$x$の範囲を定め,
その和を求めよ.
室蘭工業大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2,b_1=1$
$a_{n+1}=\dfrac{7}{3}a_n+\dfrac{4}{3}b_n+n$
$b_{n+1}=\dfrac{2}{3}a_n+\dfrac{5}{3}b_n-n$
2021室蘭工大過去問
この動画を見る
$a_1=2,b_1=1$
$a_{n+1}=\dfrac{7}{3}a_n+\dfrac{4}{3}b_n+n$
$b_{n+1}=\dfrac{2}{3}a_n+\dfrac{5}{3}b_n-n$
2021室蘭工大過去問
福田の数学〜慶應義塾大学2021年薬学部第1問(5)〜n進法と等比数列

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)3進法で表された3n桁の整数
$\overbrace{ 210210\cdots210_{(3)}}^{ 3n桁 }$
がある(ただし、nは自然数とする)。この数は、$1 \leqq k \leqq n$を満たす全て
の自然数$k$に対して、最小の位から数えて3k番目の位の数が$2、3k-1$番目の位
の数が$1、3k-2$番目の位の数が0である。この数を10進法で表した数を$a_n$
とおく。
$(\textrm{i})a_2=\boxed{\ \ ク\ \ }$である。
2021慶應義塾大学薬学部過去問
$(\textrm{ii})a_n$をnの式で表すと、$\boxed{\ \ ケ\ \ }$である。
この動画を見る
${\Large\boxed{1}}$(5)3進法で表された3n桁の整数
$\overbrace{ 210210\cdots210_{(3)}}^{ 3n桁 }$
がある(ただし、nは自然数とする)。この数は、$1 \leqq k \leqq n$を満たす全て
の自然数$k$に対して、最小の位から数えて3k番目の位の数が$2、3k-1$番目の位
の数が$1、3k-2$番目の位の数が0である。この数を10進法で表した数を$a_n$
とおく。
$(\textrm{i})a_2=\boxed{\ \ ク\ \ }$である。
2021慶應義塾大学薬学部過去問
$(\textrm{ii})a_n$をnの式で表すと、$\boxed{\ \ ケ\ \ }$である。
高専数学 微積II #32(1) 級数の和

単元:
#数Ⅱ#微分法と積分法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
等比級数
$\displaystyle \sum_{n=1}^{\infty} x^{n-1} (3-4x)^{n-1}$
が収束するように
$x$の範囲を定め和を求めよ.
この動画を見る
等比級数
$\displaystyle \sum_{n=1}^{\infty} x^{n-1} (3-4x)^{n-1}$
が収束するように
$x$の範囲を定め和を求めよ.
【高校数学】等差数列の和の公式~理解したら簡単です~ 3-4【数学B】

15三重県教員採用試験(数学:4番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$a_1=2,b_1=4$,
$a_{n+1}=3a_n+2b_n$
$b_{n+1}=4a_n+5b_n$
一般項$a_n,b_n$を求めよ.
この動画を見る
$\boxed{4}$
$a_1=2,b_1=4$,
$a_{n+1}=3a_n+2b_n$
$b_{n+1}=4a_n+5b_n$
一般項$a_n,b_n$を求めよ.
福田の数学〜慶應義塾大学2021年総合政策学部第5問〜人形を並べる方法と漸化式
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$(1)同じ人形$n$体(nは正の整数)を、1体または2体ずつ前方を向かせて列に並べる。
例えば$n=10$のとき、下図(※動画参照)のような並べ方がある。
ここで、$n$体の人形の並べ方の総数を$a_n$とすると
$a_1=1,\ a_2=2,\ a_3=3,\ldots,\ a_{12}=\boxed{\ \ アイウ\ \ },\ a_{13}=\boxed{\ \ エオカ\ \ },\ a_{14}=\boxed{\ \ キクケ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
(2)同じ人形n体(nは2以上の整数)を、2体または3体ずつ前方を向かせて列に並べる。
その並べ方の総数を$b_n$とすると
$b_2=1,\ b_3=1,\ b_4=1,\ldots,\ b_{12}=\boxed{\ \ コサシ\ \ },\ b_{13}=\boxed{\ \ スセソ\ \ },\ b_{14}=\boxed{\ \ タチツ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
2021慶應義塾大学整合政策学部過去問
この動画を見る
${\Large\boxed{5}}$(1)同じ人形$n$体(nは正の整数)を、1体または2体ずつ前方を向かせて列に並べる。
例えば$n=10$のとき、下図(※動画参照)のような並べ方がある。
ここで、$n$体の人形の並べ方の総数を$a_n$とすると
$a_1=1,\ a_2=2,\ a_3=3,\ldots,\ a_{12}=\boxed{\ \ アイウ\ \ },\ a_{13}=\boxed{\ \ エオカ\ \ },\ a_{14}=\boxed{\ \ キクケ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
(2)同じ人形n体(nは2以上の整数)を、2体または3体ずつ前方を向かせて列に並べる。
その並べ方の総数を$b_n$とすると
$b_2=1,\ b_3=1,\ b_4=1,\ldots,\ b_{12}=\boxed{\ \ コサシ\ \ },\ b_{13}=\boxed{\ \ スセソ\ \ },\ b_{14}=\boxed{\ \ タチツ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
2021慶應義塾大学整合政策学部過去問
09和歌山県教員採用試験(数学:2番 数列)
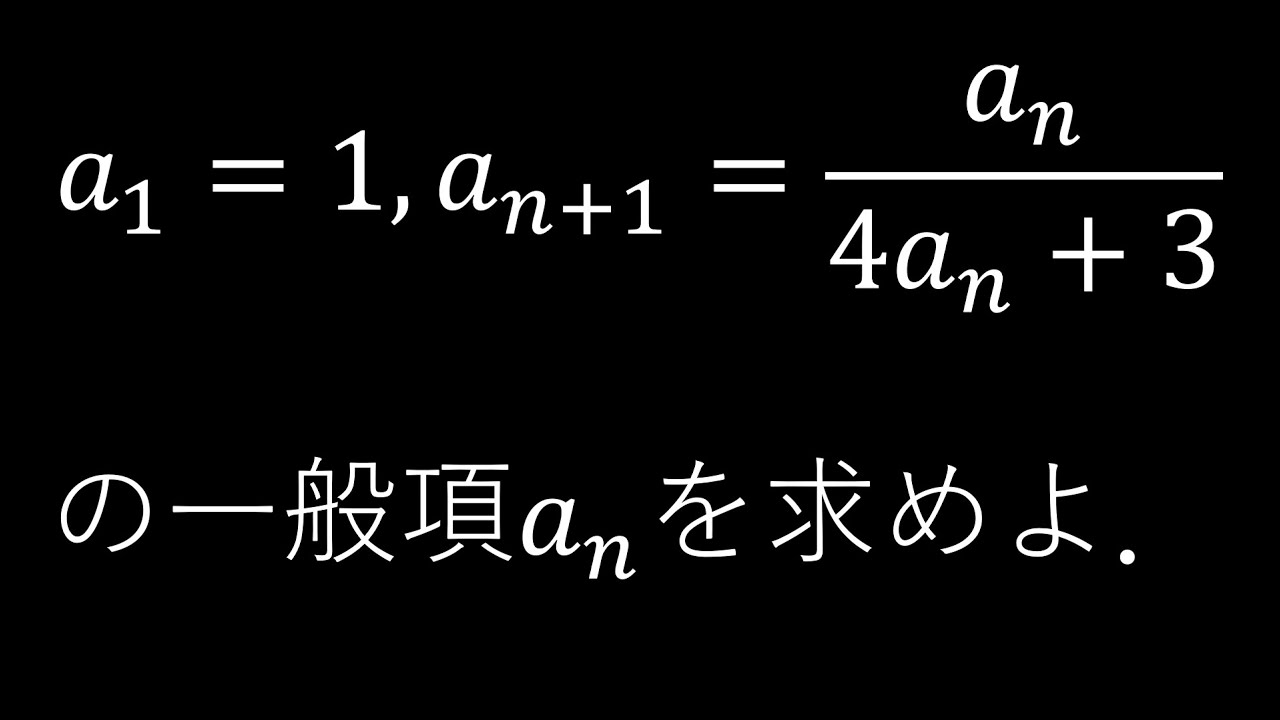
単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$a_1=1,a_{n+1}=\dfrac{a_n}{4a_n+3}$
一般項$a_n$を求めよ.
この動画を見る
$\boxed{2}$
$a_1=1,a_{n+1}=\dfrac{a_n}{4a_n+3}$
一般項$a_n$を求めよ.
名古屋市立大(医)漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$a_1=2$
$\dfrac{a_{n+1}}{a_n}=\dfrac{n}{n+2}$
$\displaystyle \sum_{n=1}^{\infty}a_n$を求めよ.
名古屋市立(医)過去問
この動画を見る
$n$を自然数とする.
$a_1=2$
$\dfrac{a_{n+1}}{a_n}=\dfrac{n}{n+2}$
$\displaystyle \sum_{n=1}^{\infty}a_n$を求めよ.
名古屋市立(医)過去問
高専数学 微積II #11 級数の和
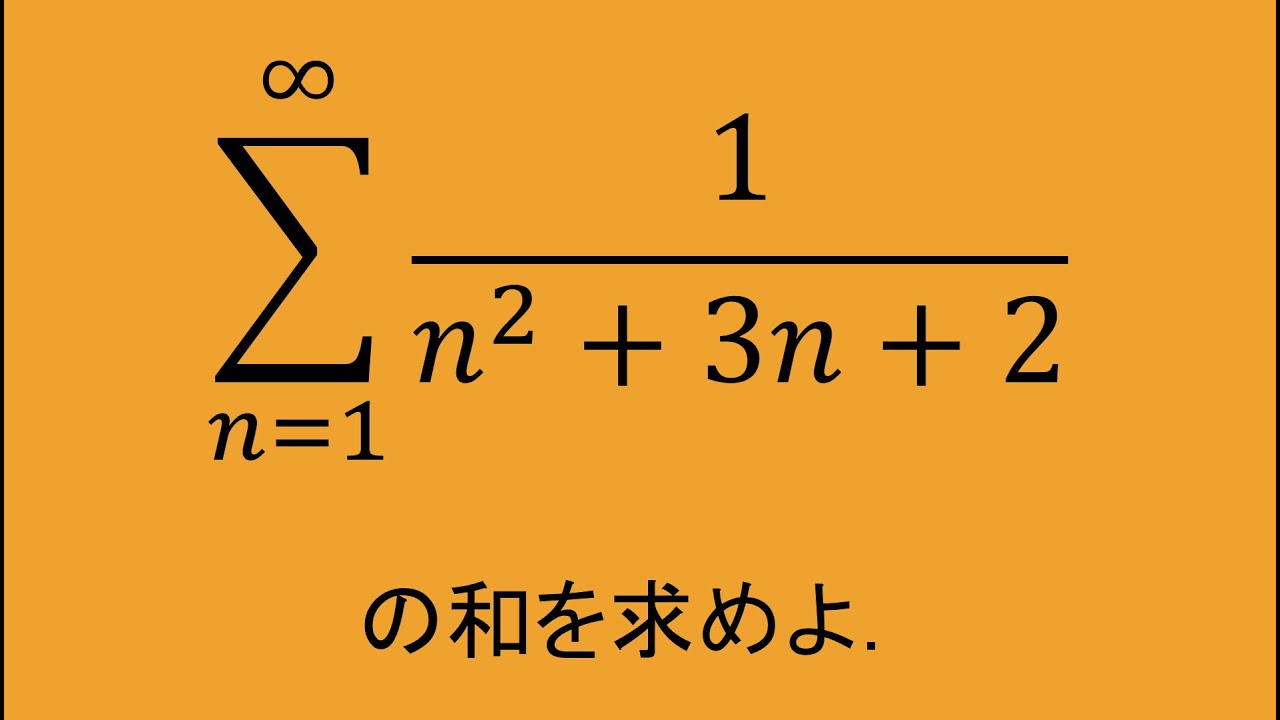
単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#微分法と積分法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
級数
$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{n^2+3n+2}$
の和を求めよ.
この動画を見る
級数
$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{n^2+3n+2}$
の和を求めよ.
福田の数学〜慶應義塾大学2021年商学部第4問〜数列の文章題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$座標平面上でx座標とy座標がいずれも整数である点を格子点と呼ぶ。それぞれ
の正の整数nについて、4つの格子点$A_n(n,n),\ B_n(-n,n),\ C_n(-n,-n),\ D_n(n,-n)$
が作る正方形をJ_nとする。また、$(n-1,n)$にある格子点を$P_n$とする。
$\left\{a_k\right\}$を初項$a_1$が$-56$で、交差が$\frac{1}{4}$の等差数列とし、数列$\left\{a_k\right\}$の各項を以下の
ようにして格子点上順番に割り当てていく。
1.初項$a_1$は格子点$P_1$に割り当てる。
2.$a_l$が正方形$J_m$の周上にある格子点で$A_m$以外の点に割り当てられているときには、
$J_m$の周上でその点から半時計回り(右図(※動画参照)での矢印が示す方向)に一つ移動
した格子点に$a_{l+1}$を割り当てる。
3$.a_l$が格子点$A_m$に割り当てられているときには、$a_{l+1}$を格子点$P_{m+1}$に割り当てる。
全体としては、図に示されているようにして、格子点をたどっていくことになる。
(1)格子点$P_n$に割り当てられる数列$\left\{a_k\right\}$の項を$p_n$とし、格子点$C_n$に割り当て
られる数列$\left\{a_k\right\}$の項を$c_n$とする。
このとき、$p_4=-\boxed{\ \ アイ\ \ }, c_4=-\frac{\boxed{\ \ ウエオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)上で定めた$p_n$を用いて、$q_n$を数列$\left\{p_n\right\}$の初項$p_1$から第n項$p_n$までの和とする。
$q_n$をnを使って表すと、$q_n=\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}n^3-\frac{\boxed{\ \ ケコサ\ \ }}{\boxed{\ \ シ\ \ }}n$である。
(3)上で定めた$q_n$が最小値を取るのは、$n=\boxed{\ \ ス\ \ }$または$n=\boxed{\ \ セ\ \ }$のときであり、
その値は#$-\boxed{\ \ ソタチ\ \ }$である。
2021慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{4}}$座標平面上でx座標とy座標がいずれも整数である点を格子点と呼ぶ。それぞれ
の正の整数nについて、4つの格子点$A_n(n,n),\ B_n(-n,n),\ C_n(-n,-n),\ D_n(n,-n)$
が作る正方形をJ_nとする。また、$(n-1,n)$にある格子点を$P_n$とする。
$\left\{a_k\right\}$を初項$a_1$が$-56$で、交差が$\frac{1}{4}$の等差数列とし、数列$\left\{a_k\right\}$の各項を以下の
ようにして格子点上順番に割り当てていく。
1.初項$a_1$は格子点$P_1$に割り当てる。
2.$a_l$が正方形$J_m$の周上にある格子点で$A_m$以外の点に割り当てられているときには、
$J_m$の周上でその点から半時計回り(右図(※動画参照)での矢印が示す方向)に一つ移動
した格子点に$a_{l+1}$を割り当てる。
3$.a_l$が格子点$A_m$に割り当てられているときには、$a_{l+1}$を格子点$P_{m+1}$に割り当てる。
全体としては、図に示されているようにして、格子点をたどっていくことになる。
(1)格子点$P_n$に割り当てられる数列$\left\{a_k\right\}$の項を$p_n$とし、格子点$C_n$に割り当て
られる数列$\left\{a_k\right\}$の項を$c_n$とする。
このとき、$p_4=-\boxed{\ \ アイ\ \ }, c_4=-\frac{\boxed{\ \ ウエオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)上で定めた$p_n$を用いて、$q_n$を数列$\left\{p_n\right\}$の初項$p_1$から第n項$p_n$までの和とする。
$q_n$をnを使って表すと、$q_n=\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}n^3-\frac{\boxed{\ \ ケコサ\ \ }}{\boxed{\ \ シ\ \ }}n$である。
(3)上で定めた$q_n$が最小値を取るのは、$n=\boxed{\ \ ス\ \ }$または$n=\boxed{\ \ セ\ \ }$のときであり、
その値は#$-\boxed{\ \ ソタチ\ \ }$である。
2021慶應義塾大学商学部過去問
