 数B
数B
 数B
数B
【数B】【確率分布と統計的な推測】正規分布6 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある試験での成績の結果は、平均71点、標準偏差8点であった。得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1) 63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1)のとき、合格点を55点とすると、約何人が合格することになるか。
この動画を見る
ある試験での成績の結果は、平均71点、標準偏差8点であった。得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1) 63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1)のとき、合格点を55点とすると、約何人が合格することになるか。
【数B】【確率分布と統計的な推測】正規分布5 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1000人の生徒に数学のテストを行ったところ、その成績は、平均48点,標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
この動画を見る
1000人の生徒に数学のテストを行ったところ、その成績は、平均48点,標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
【数B】【確率分布と統計的な推測】正規分布4 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある県における高校2年生の男子の身長が、平均170.0cm,標準偏差5.2 cm の正規分布に従うものとする。
(1) 身長が165cm以上の生徒は、約何%いるか。整数値で答えよ。
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
この動画を見る
ある県における高校2年生の男子の身長が、平均170.0cm,標準偏差5.2 cm の正規分布に従うものとする。
(1) 身長が165cm以上の生徒は、約何%いるか。整数値で答えよ。
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
【数B】【確率分布と統計的な推測】正規分布3 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布N(m,δ²)に従う確率変数Xについて、Xのとる値を
m-1.5δ, m-0.5δ, m+0.5δ, m+1.5δ
によって、5つの階級に分けると、各階級に何%ずつ含まれるか。
この動画を見る
正規分布N(m,δ²)に従う確率変数Xについて、Xのとる値を
m-1.5δ, m-0.5δ, m+0.5δ, m+1.5δ
によって、5つの階級に分けると、各階級に何%ずつ含まれるか。
【数B】【確率分布と統計的な推測】正規分布2 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布N (10,5²)に従う確率変数について、次の等式が成り立つように、 定数の値を定めよ。
(1) P(10 ≦ X ≦ a) = 0.4772
(2) P(X ≧ a) = 0.0082
(3) P(|X - 10| ≦ a) = 0.8664
(4) P(|X - 10| ≦ a) = 0.0278
正規分布N(m、δ²)において、変数Xが|X - m|≦kδ の範囲に入る確率が、
次の値になるように、正の定数の値を定めよ。
(1) 0.006
(2) 0.016
(3) 0.242
この動画を見る
正規分布N (10,5²)に従う確率変数について、次の等式が成り立つように、 定数の値を定めよ。
(1) P(10 ≦ X ≦ a) = 0.4772
(2) P(X ≧ a) = 0.0082
(3) P(|X - 10| ≦ a) = 0.8664
(4) P(|X - 10| ≦ a) = 0.0278
正規分布N(m、δ²)において、変数Xが|X - m|≦kδ の範囲に入る確率が、
次の値になるように、正の定数の値を定めよ。
(1) 0.006
(2) 0.016
(3) 0.242
【数B】【確率分布と統計的な推測】正規分布1 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率変数Xのとる値の範囲が-1≦x≦1で、その確率密度関数f(x)が f(x)-1-x(-1≦x≦1) で与えられるとき、次の確率を求めよ。
(1) P(0 ≦ X ≦ 0.25)
(2) P(X≦0.25)
(3) P(- 0.5 ≦ X ≦ 0.3)
確率変数Xのとる値の範囲が0≤x≤10で、その確率密度関数がkを定数として f(x) = kx(10 - x) (0≦x≦10) で与えられるとする。
このとき、kの値は□であり、確率 P(3 ≦ X ≦ 7) は□となる。
この動画を見る
確率変数Xのとる値の範囲が-1≦x≦1で、その確率密度関数f(x)が f(x)-1-x(-1≦x≦1) で与えられるとき、次の確率を求めよ。
(1) P(0 ≦ X ≦ 0.25)
(2) P(X≦0.25)
(3) P(- 0.5 ≦ X ≦ 0.3)
確率変数Xのとる値の範囲が0≤x≤10で、その確率密度関数がkを定数として f(x) = kx(10 - x) (0≦x≦10) で与えられるとする。
このとき、kの値は□であり、確率 P(3 ≦ X ≦ 7) は□となる。
【数B】【確率分布と統計的な推測】二項分布 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,Bの2人が,白玉2個と赤玉3個の入っている袋から,A,Bの順に玉を1個ずつ取り出していき,最初に白玉を取り出した人を勝ちとする。ただし,取り出した玉はもとに戻さないものとする。この勝負を20回行うとき,Aが勝つ回数Xの期待値と標準偏差を求めよ。
この動画を見る
A,Bの2人が,白玉2個と赤玉3個の入っている袋から,A,Bの順に玉を1個ずつ取り出していき,最初に白玉を取り出した人を勝ちとする。ただし,取り出した玉はもとに戻さないものとする。この勝負を20回行うとき,Aが勝つ回数Xの期待値と標準偏差を求めよ。
福田のおもしろ数学400〜2項展開の係数と次数に関する個数

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか?
この動画を見る
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか?
【数B】【確率分布と統計的な推測】独立な確率変数と期待値、分散 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの事象A,Bが独立であって,P(A)=1/2,P(B)=1/3であるとき,次の問いに答えよ。
(1)A,Bのうち少なくとも一方が起こる確率を求めよ。
(2) A,Bのうちどちらか一方のみが起こる確率を求めよ。
2,4,6の目が2面ずつ書かれた3個のさいころを同時に投げるとき,出る目の積の期待値を求めよ。
1つの面には1,2つの面には2,3つの面には3が書かれているさいころを2回投げて,1回目に出た目の数を十の位,2回目に出た目の数を一の位として得られる2桁の数をXとする。
(1)Xの確率分布を求めよ。
(2)Xの期待値と分散を求めよ。
この動画を見る
2つの事象A,Bが独立であって,P(A)=1/2,P(B)=1/3であるとき,次の問いに答えよ。
(1)A,Bのうち少なくとも一方が起こる確率を求めよ。
(2) A,Bのうちどちらか一方のみが起こる確率を求めよ。
2,4,6の目が2面ずつ書かれた3個のさいころを同時に投げるとき,出る目の積の期待値を求めよ。
1つの面には1,2つの面には2,3つの面には3が書かれているさいころを2回投げて,1回目に出た目の数を十の位,2回目に出た目の数を一の位として得られる2桁の数をXとする。
(1)Xの確率分布を求めよ。
(2)Xの期待値と分散を求めよ。
【数B】【確率分布と統計的な推測】確率変数の和と期待値 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
トランプのハート13枚を裏返しにしてよく混ぜてから,まずAが3枚抜き,抜いたカードはもとに戻さずに,続けてBが1枚抜くとき,A,Bが抜いた絵札の枚数を,それぞれX,Yとする。XとYの同時分布を求めよ。
100本のくじの中に30本の当たりくじがある。このくじから10本のくじを続けて引くとき,その中の当たりくじの本数をYとする。確率変数Yの期待値を求めよ。ただし,引いたくじはもとに戻さないとする。
この動画を見る
トランプのハート13枚を裏返しにしてよく混ぜてから,まずAが3枚抜き,抜いたカードはもとに戻さずに,続けてBが1枚抜くとき,A,Bが抜いた絵札の枚数を,それぞれX,Yとする。XとYの同時分布を求めよ。
100本のくじの中に30本の当たりくじがある。このくじから10本のくじを続けて引くとき,その中の当たりくじの本数をYとする。確率変数Yの期待値を求めよ。ただし,引いたくじはもとに戻さないとする。
【数B】【確率分布と統計的な推測】確率変数の期待値と分散3 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1と書かれたカードが2枚,2と書かれたカードが2枚,4と書かれたカードが1枚,計5枚のカードがある。この中から2枚のカードを取り出し,それらに書かれている数の和をXとするとき,確率変数Xの期待値と分散を求めよ。
この動画を見る
1と書かれたカードが2枚,2と書かれたカードが2枚,4と書かれたカードが1枚,計5枚のカードがある。この中から2枚のカードを取り出し,それらに書かれている数の和をXとするとき,確率変数Xの期待値と分散を求めよ。
【数B】【確率分布と統計的な推測】確率変数の期待値と分散2 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
白玉6個と赤玉4個が入っている袋から玉を次の方法で取り出す。白玉の出た回数をXとするとき,Xの期待値と分散をそれぞれ求めよ。
(1)1個ずつ,もとに戻さず2回続けて取り出す。
(2)1個ずつ,2回取り出す。ただし,取り出した玉は毎回もとに戻す。
この動画を見る
白玉6個と赤玉4個が入っている袋から玉を次の方法で取り出す。白玉の出た回数をXとするとき,Xの期待値と分散をそれぞれ求めよ。
(1)1個ずつ,もとに戻さず2回続けて取り出す。
(2)1個ずつ,2回取り出す。ただし,取り出した玉は毎回もとに戻す。
【数B】【確率分布と統計的な推測】確率変数と確率分布 ※問題文は概要欄

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
4枚の硬貨を同時に投げる試行を4回繰り返すとき,2枚が表で2枚が裏となる回数をXとする。P(X=k)(k=0,1,2,3,4)の式を求めよ。
4つの箱があり、その箱に,それぞれ1,2,3,4の番号がつけられている。1,2,3,4の番号がつけられている4枚のカードを1つの箱に1枚ずつ入れるとき,カードの番号と箱の番号が一致したものの個数をXとする。このとき,Xの確率分布と,P(X>2), P(X≦2)を求めよ。
この動画を見る
4枚の硬貨を同時に投げる試行を4回繰り返すとき,2枚が表で2枚が裏となる回数をXとする。P(X=k)(k=0,1,2,3,4)の式を求めよ。
4つの箱があり、その箱に,それぞれ1,2,3,4の番号がつけられている。1,2,3,4の番号がつけられている4枚のカードを1つの箱に1枚ずつ入れるとき,カードの番号と箱の番号が一致したものの個数をXとする。このとき,Xの確率分布と,P(X>2), P(X≦2)を求めよ。
福田のおもしろ数学383〜関数方程式

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
この動画を見る
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
福田のおもしろ数学378〜ある漸化式で定められる数列の最初の2025項が正で2026番目が初めて負になることが可能かどうかの検証

単元:
#数Ⅱ#三角関数#加法定理とその応用#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
この動画を見る
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
福田のおもしろ数学374〜365と366を1から365までの整数で割った余りの総和の大小比較

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式
指導講師:
福田次郎
問題文全文(内容文):
$360$を$1,2,3,…,365$で割った余りの総和を$A$、$366$を$1,2,3,…,365$で割った余りの総和を$B$とする。$A$と$B$の大小を比較せよ。
この動画を見る
$360$を$1,2,3,…,365$で割った余りの総和を$A$、$366$を$1,2,3,…,365$で割った余りの総和を$B$とする。$A$と$B$の大小を比較せよ。
福田のおもしろ数学371〜初項が素数で漸化式で定義された数列が素数でない項をもつ証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1=p$(素数), $a_{n+1}=2a_n-1$で定まる数列には素数でない項が存在する。証明せよ。
この動画を見る
$a_1=p$(素数), $a_{n+1}=2a_n-1$で定まる数列には素数でない項が存在する。証明せよ。
【中学数学】標本調査の問題演習~標準問題~【中3数学】

単元:
#数学(中学生)#中3数学#統計的な推測#標本調査
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)
白と黒の玉が合わせて500個入った袋がある。
この袋の中から30個を無作為に取り出すと、そのうちの12個が白い玉だった。袋の中の白い球はおよそ何個と表されるか?
(2)
池にいる魚の数を調べる。
1度20匹捕まえて印をつけ池に戻し
1週間後、今度は60匹の魚を捕まえたところ
そのうち4匹の魚に印がついていました。
この池には何匹の魚がいると考えられる?
この動画を見る
(1)
白と黒の玉が合わせて500個入った袋がある。
この袋の中から30個を無作為に取り出すと、そのうちの12個が白い玉だった。袋の中の白い球はおよそ何個と表されるか?
(2)
池にいる魚の数を調べる。
1度20匹捕まえて印をつけ池に戻し
1週間後、今度は60匹の魚を捕まえたところ
そのうち4匹の魚に印がついていました。
この池には何匹の魚がいると考えられる?
福田のおもしろ数学366〜漸化式で定義された数列の周期性を示す

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列 ${x_n}$ が $x_1$ を正の整数とし、
$
x_{n+1} =
\begin{cases}
\frac{1}{2}x_n & (x_n\text{ が偶数})\\
a+x_n & (x_n\text{ が奇数})
\end{cases}
$
($a$ は正の奇数) を満たしている。この数列の周期性を示せ。
この動画を見る
数列 ${x_n}$ が $x_1$ を正の整数とし、
$
x_{n+1} =
\begin{cases}
\frac{1}{2}x_n & (x_n\text{ が偶数})\\
a+x_n & (x_n\text{ が奇数})
\end{cases}
$
($a$ は正の奇数) を満たしている。この数列の周期性を示せ。
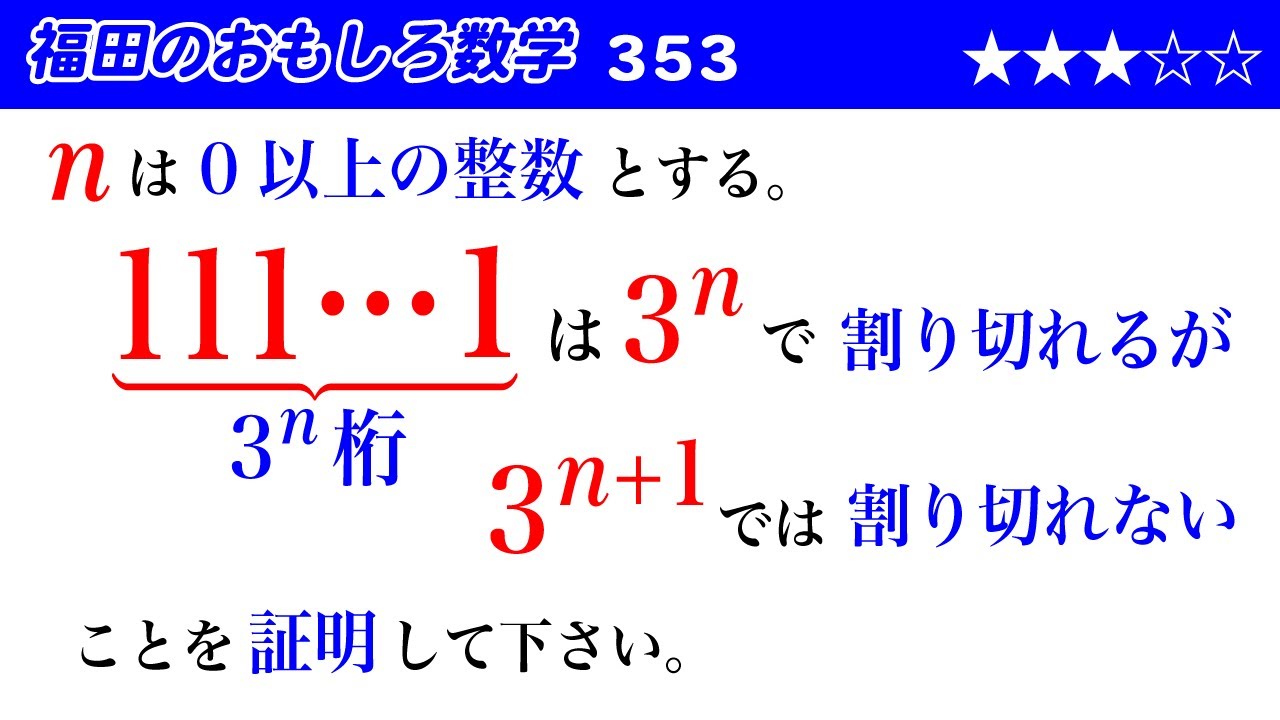
福田のおもしろ数学353〜1が連続3^n個並ぶ数は3^nで割り切れることの証明
単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
この動画を見る
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
不等式の証明の難問!記号が多すぎる。。。 #Shorts #ずんだもん #勉強 #数学

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#お茶の水女子大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
mを2以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
この動画を見る
mを2以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
福田のおもしろ数学351〜漸化式で定まる数列の第2025項の取り得る値の個数

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1 = 1, a_{n+1} + a_n = ( a_{n+1} - a_n )^2$ で定まる、すべての項が正の数列 $\{ a_n \}$ に対し $a_2025$ の取りうる値は何個あるか。
この動画を見る
$a_1 = 1, a_{n+1} + a_n = ( a_{n+1} - a_n )^2$ で定まる、すべての項が正の数列 $\{ a_n \}$ に対し $a_2025$ の取りうる値は何個あるか。
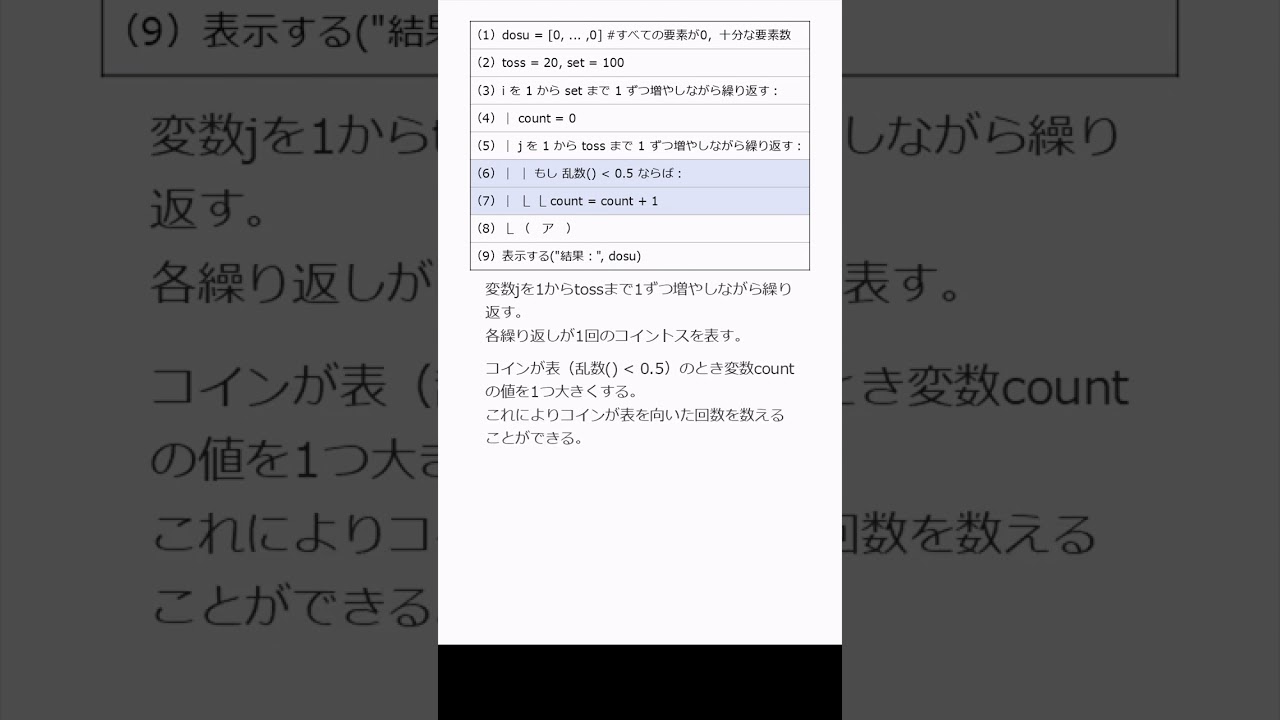
324 コイン投げの結果を度数分布表にまとめる:ばらつきを可視化しよう!
福田のおもしろ数学339〜自然数の列から平方数を除いてできる列の第2024項の値

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
この動画を見る
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
福田のおもしろ数学323〜小数部分の和を不等式で評価する

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
この動画を見る
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
福田の数学〜北里大学2024医学部第3問〜確率漸化式

単元:
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
箱Aには赤玉2個、白玉1個入っており、箱Bには白玉3個が入っている。2つの箱A、Bについて、次の操作を繰り返す。
(操作)2つの箱A,Bからそれぞれ1個ずつ玉を同時に取り出し、箱Aから取り出した玉を箱Bに入れて、箱Bから取り出した玉を箱Aに入れる。
n回目の操作を終えたときに箱Aに入っている赤玉の個数が2個、1個、0個である確率をそれぞれ$p_n,q_n,r_n$とする。
(1)$p_1,q_1,p_2,q_2$を求め、$r_n$を$p_n$と$q_n$を用いて表せ。
(2)$p_{n+1}$を$p_n,q_n$で表せ。また$q_{n+1}$を$q_n$を用いて表せ。
(3)$q_n$を求めよ。
(4)$s_n=3^np_n$とおいて、$s_n$を求めよ。また、$p_n$を求めよ。
この動画を見る
箱Aには赤玉2個、白玉1個入っており、箱Bには白玉3個が入っている。2つの箱A、Bについて、次の操作を繰り返す。
(操作)2つの箱A,Bからそれぞれ1個ずつ玉を同時に取り出し、箱Aから取り出した玉を箱Bに入れて、箱Bから取り出した玉を箱Aに入れる。
n回目の操作を終えたときに箱Aに入っている赤玉の個数が2個、1個、0個である確率をそれぞれ$p_n,q_n,r_n$とする。
(1)$p_1,q_1,p_2,q_2$を求め、$r_n$を$p_n$と$q_n$を用いて表せ。
(2)$p_{n+1}$を$p_n,q_n$で表せ。また$q_{n+1}$を$q_n$を用いて表せ。
(3)$q_n$を求めよ。
(4)$s_n=3^np_n$とおいて、$s_n$を求めよ。また、$p_n$を求めよ。
数学「大学入試良問集」【13−10 群数列とその戦略】を宇宙一わかりやすく

単元:
#数列#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$1,1,3,1,3,5,1,3,5,7,1,3,5,7,9,1,・・・$において、次の問いに答えよ。
ただし、$k,m,n$は自然数とする。
(1)$k+1$回目に現れる1は第何項か。
(2)$m$回目に現れる17は第何項か。
(3)初項から$k+1$回目の1までの項の和を求めよ。
(4)初項から第$n$項までの和を$S_n$とするとき、$S_n \gt 1300$となる最小の$n$を求めよ。
この動画を見る
数列$1,1,3,1,3,5,1,3,5,7,1,3,5,7,9,1,・・・$において、次の問いに答えよ。
ただし、$k,m,n$は自然数とする。
(1)$k+1$回目に現れる1は第何項か。
(2)$m$回目に現れる17は第何項か。
(3)初項から$k+1$回目の1までの項の和を求めよ。
(4)初項から第$n$項までの和を$S_n$とするとき、$S_n \gt 1300$となる最小の$n$を求めよ。
この求め方知ってた?

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図のように1辺1cmの正方形を並べて図形を作る。このときn番目図形の周の長さを求めよ。
※図は動画内参照
この動画を見る
図のように1辺1cmの正方形を並べて図形を作る。このときn番目図形の周の長さを求めよ。
※図は動画内参照
福田のおもしろ数学316〜x^n+x^{-n}が整数である証明と倍数

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
この動画を見る
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
福田の数学〜早稲田大学2024社会科学部第3問〜集合と数列

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
この動画を見る
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
