 数列の極限
数列の極限
 数列の極限
数列の極限
これどゆこと?

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
五条悟の無下限呪術がアキレスと亀らしんですが,どういうことですか?
この動画を見る
五条悟の無下限呪術がアキレスと亀らしんですが,どういうことですか?
工夫が必要な極限問題 By 英語orドイツ語シはBかHか さん #極限
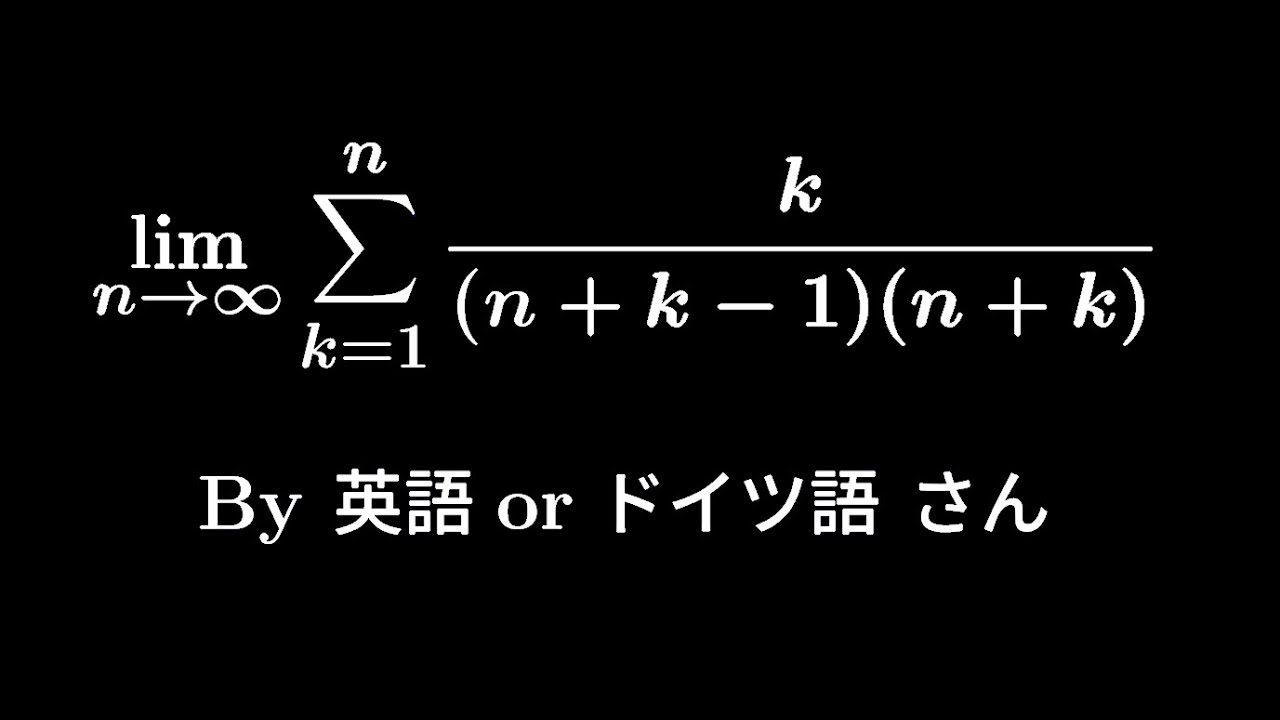
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{(n+k-1)(n+k)}$
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{(n+k-1)(n+k)}$
福田の数学〜上智大学2023年TEAP利用型理系第1問(3)〜連立漸化式と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
この動画を見る
$\Large{\boxed{1}}$ (3)$a_1$=0, $b_1$=6とし、
$a_{n+1}$=$\displaystyle\frac{a_n+b_n}{2}$, $b_{n+1}$=$a_n$ ($n$≧1)
で定まる$a_n$, $b_n$を用いて、平面上の点$P_n$($a_n$, $b_n$)($n$=1,2,3,...)を定める。
(i)点$P_n$は常に直線$y$=$\boxed{\ \ ウ\ \ }x$+$\boxed{\ \ エ\ \ }$上にある。
(ii)$n$を限りなく大きくするとき、点$P_n$は点$\left(\boxed{\ \ オ\ \ }, \boxed{\ \ カ\ \ }\right)$に限りなく近づく。
福田の数学〜青山学院大学2023年理工学部第5問〜定積分で定義された数列と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
この動画を見る
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
福田の数学〜慶應義塾大学2023年理工学部第4問〜定積分と不等式Part2
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
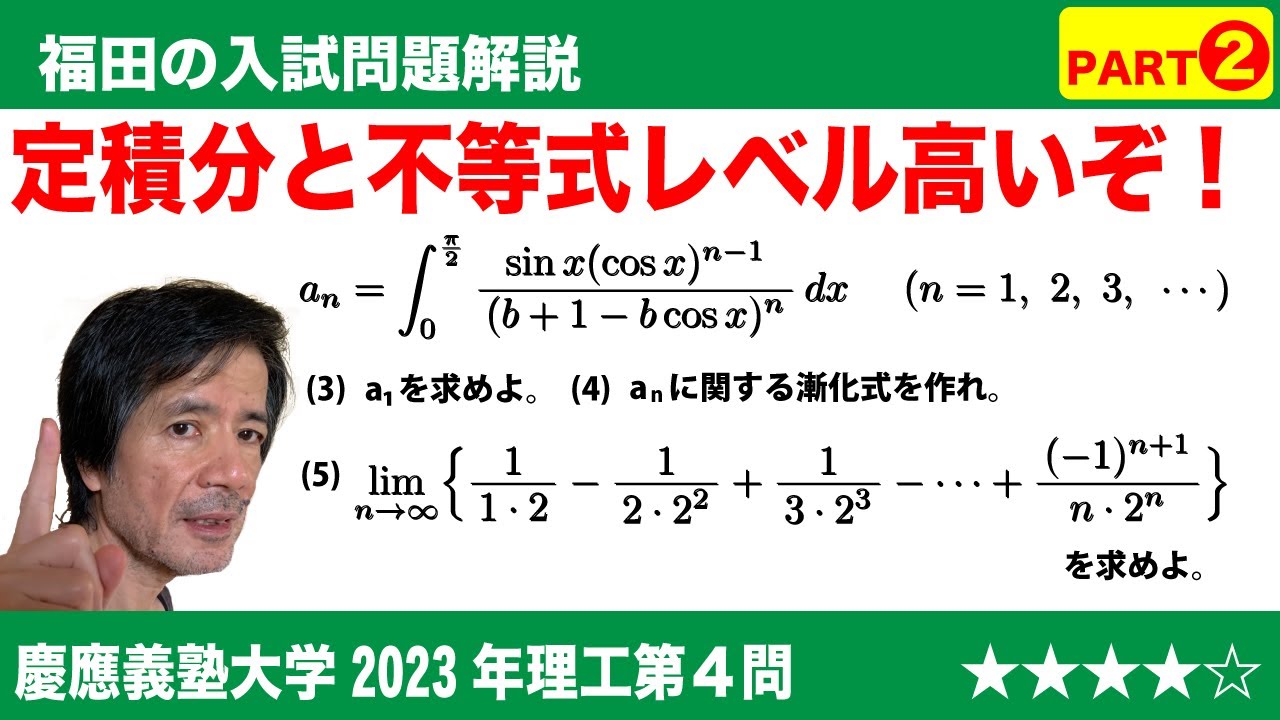
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
大学入試問題#598「計算が大変でした」 関西大学(2009) #区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
福田の数学〜東京医科歯科大学2023年医学部第2問PART2〜場合分けされた連立漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第2問PART1〜場合分けされた連立漸化式

単元:
#大学入試過去問(数学)#漸化式#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
大学入試問題#595「山口大学に初挑戦!」 山口大学(2014) #数列

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_n=\tan\displaystyle \frac{\pi}{2^{n+1}}$のとき
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{a_{n+1}}{a_n}$を求めよ
出典:2014年山口大学 入試問題
この動画を見る
$a_n=\tan\displaystyle \frac{\pi}{2^{n+1}}$のとき
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{a_{n+1}}{a_n}$を求めよ
出典:2014年山口大学 入試問題
大学入試問題#593「計算ミスに気をつける」 福島大学(1987) #極限

単元:
#大学入試過去問(数学)#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n}{(2n+k)^2}log\displaystyle \frac{n+2k}{n}$
出典:1987年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n}{(2n+k)^2}log\displaystyle \frac{n+2k}{n}$
出典:1987年福島大学 入試問題
長岡技術科大 ナイスな問題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
2008長岡技術科学大学過去問題
①$\displaystyle\sum_{n=2}^{\infty}\frac{1}{n^2-\frac{1}{4}}$を求めよ
②$\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}<\frac{5}{3}$を示せ
この動画を見る
2008長岡技術科学大学過去問題
①$\displaystyle\sum_{n=2}^{\infty}\frac{1}{n^2-\frac{1}{4}}$を求めよ
②$\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}<\frac{5}{3}$を示せ
大学入試問題#589「一度は解いておきたい良問」 奈良女子大学(2004) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1\times a_2\times・・・\times a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$のとき
$\displaystyle \sum_{n=1}^\infty a_n$を求めよ
出典:2004年奈良女子大学 入試問題
この動画を見る
$a_1\times a_2\times・・・\times a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$のとき
$\displaystyle \sum_{n=1}^\infty a_n$を求めよ
出典:2004年奈良女子大学 入試問題
大阪市立大 いい問題

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2021大阪市立大学
単位円に内接する正n角形の面積を$A_n$
単位円に内接する正n角形の各辺の中点を結んでできる正n角形の面積を$B_n$
①②$A_n$,$B_n$をnを用いて
③$\displaystyle\lim_{n \to \infty}B_n$を求めよ
④$n \geqq 32$のとき$\frac{B_n}{A_n}>\frac{99}{100}$を示せ
この動画を見る
2021大阪市立大学
単位円に内接する正n角形の面積を$A_n$
単位円に内接する正n角形の各辺の中点を結んでできる正n角形の面積を$B_n$
①②$A_n$,$B_n$をnを用いて
③$\displaystyle\lim_{n \to \infty}B_n$を求めよ
④$n \geqq 32$のとき$\frac{B_n}{A_n}>\frac{99}{100}$を示せ
福田の数学〜立教大学2023年理学部第4問〜数学的帰納法とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#数学的帰納法#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
この動画を見る
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
【演習編!】演習で無限等比級数の知識をどう使う?!【数学III】

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
3rd School
問題文全文(内容文):
(1)$\displaystyle \sum_{n=1}^\infty \frac{1}{2}(\frac{5}{4})^{n-1}$
(2)$\displaystyle \sum_{n=1}^\infty \frac{4^n-3^{n+1}}{3^{2n}}$
この動画を見る
(1)$\displaystyle \sum_{n=1}^\infty \frac{1}{2}(\frac{5}{4})^{n-1}$
(2)$\displaystyle \sum_{n=1}^\infty \frac{4^n-3^{n+1}}{3^{2n}}$
福田の数学〜九州大学2023年理系第2問〜数列の収束発散の判定

単元:
#大学入試過去問(数学)#数列#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $\alpha$を実数とする。数列$\left\{a_n\right\}$が
$a_1$=$\alpha$, $a_{n+1}$=|$a_n$-1|+$a_n$-1 (n=1,2,3,...)
で定められるとき、以下の問いに答えよ。
(1)$\alpha$≦1のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(2)$\alpha$>2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(3)1<$\alpha$<$\frac{3}{2}$のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(4)$\frac{3}{2}≦\alpha$<2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{2}$ $\alpha$を実数とする。数列$\left\{a_n\right\}$が
$a_1$=$\alpha$, $a_{n+1}$=|$a_n$-1|+$a_n$-1 (n=1,2,3,...)
で定められるとき、以下の問いに答えよ。
(1)$\alpha$≦1のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(2)$\alpha$>2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(3)1<$\alpha$<$\frac{3}{2}$のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(4)$\frac{3}{2}≦\alpha$<2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
2023九州大学理系過去問
産業医科大 区分求積法を使わなくても出せるよ

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+・・・・+n^4}{n^5}$
これを求めよ。
産業医科大過去問
この動画を見る
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+・・・・+n^4}{n^5}$
これを求めよ。
産業医科大過去問
早稲田大 みんな大好きBBB

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
この動画を見る
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
【等比数列の極限!】無限等比級数の基礎と求め方を解説!【数学III】

【和の極限】無限級数の基礎と求め方を解説!【数学III】

福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
目で見てわかる収束の値

単元:
#関数と極限#数列の極限#関数の極限#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{4}+\dfrac{1}{4^2}+\dfrac{1}{4^3}+\dfrac{1}{4^4}+・・・・・・+\dfrac{1}{4^n}$
これは収束する値か?
この動画を見る
$\dfrac{1}{4}+\dfrac{1}{4^2}+\dfrac{1}{4^3}+\dfrac{1}{4^4}+・・・・・・+\dfrac{1}{4^n}$
これは収束する値か?
大学入試問題#505「綺麗な数列の問題」 #神戸大学 (2022) #数列 #極限
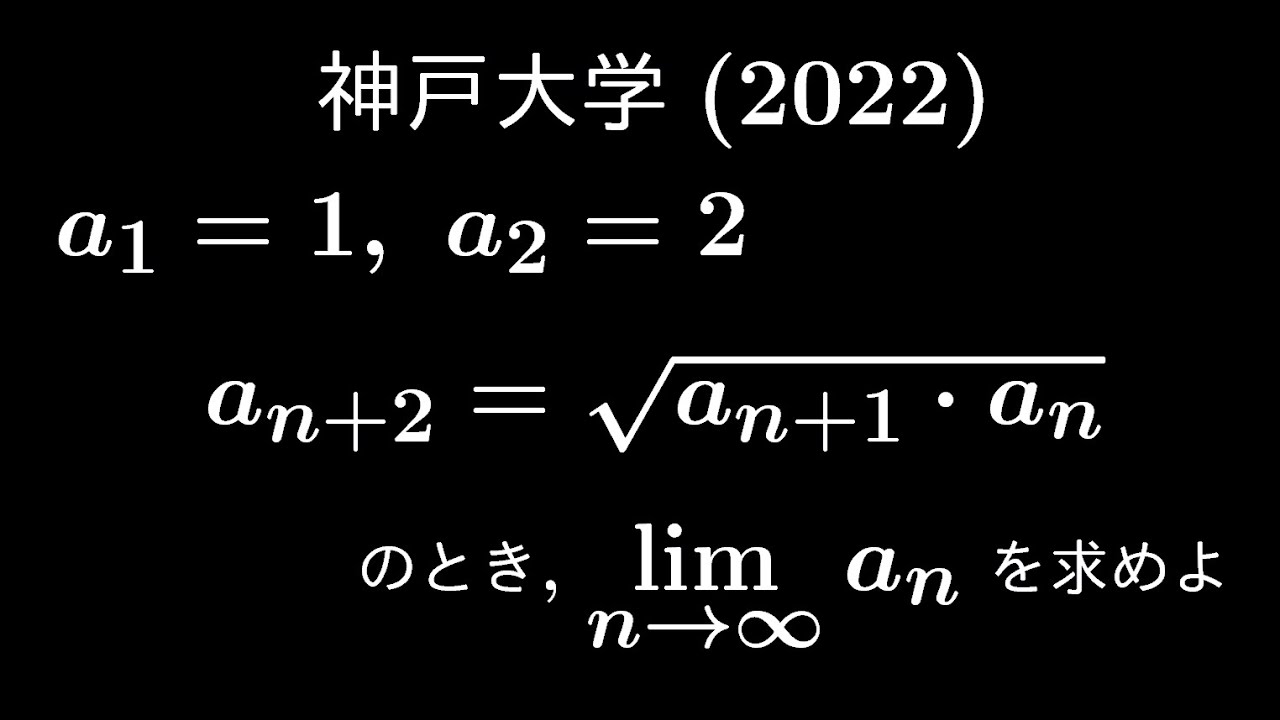
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_{n+1}・a_n }$のとき
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2022年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_{n+1}・a_n }$のとき
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2022年神戸大学 入試問題
福田の数学〜北海道大学2023年理系第1問〜複素数平面上の図形の列

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
【0≦θ≦πを問題文に追加】微分すると大変かも・・・ By ~らん~
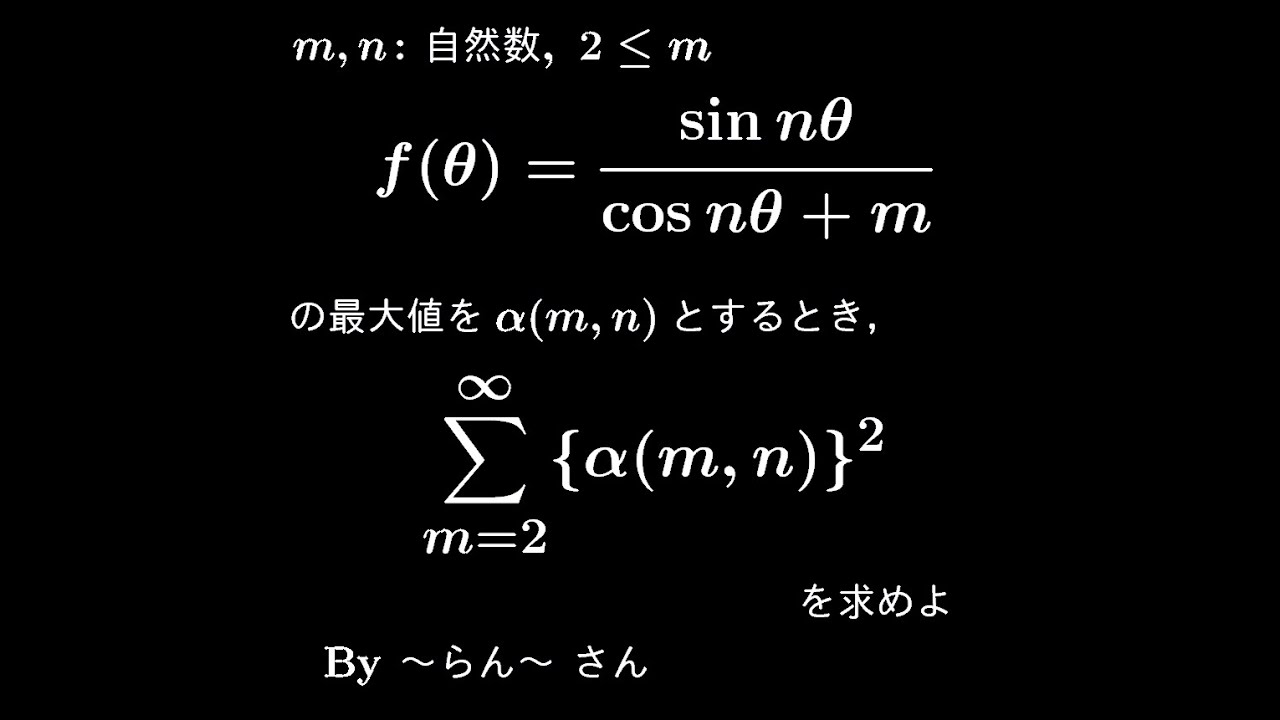
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
この動画を見る
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
福田の数学〜大阪大学2023年理系第1問〜不等式の証明と極限

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#関数と極限#微分とその応用#数列の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ nを2以上の自然数とする。
(1)0≦x≦1のとき、次の不等式が成り立つことを示せ。
$\frac{1}{2}x^2$≦$\displaystyle(-1)^n\left\{\frac{1}{x+1}-1-\sum\_{k=2}^n(-x)^{k-1}\right\}$≦$x^n-\frac{1}{2}x^{n+1}$
(2)$a_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{k}$ とするとき、次の極限値を求めよ。
$\displaystyle\lim_{n \to \infty}(-1)^nn(a_n-\log 2)$
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{5}$ nを2以上の自然数とする。
(1)0≦x≦1のとき、次の不等式が成り立つことを示せ。
$\frac{1}{2}x^2$≦$\displaystyle(-1)^n\left\{\frac{1}{x+1}-1-\sum\_{k=2}^n(-x)^{k-1}\right\}$≦$x^n-\frac{1}{2}x^{n+1}$
(2)$a_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{k}$ とするとき、次の極限値を求めよ。
$\displaystyle\lim_{n \to \infty}(-1)^nn(a_n-\log 2)$
2023大阪大学理系過去問
大学入試問題#465「よくある極限問題」 電気通信大学2009 #極限

単元:
#大学入試過去問(数学)#三角関数#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典:2009年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典:2009年電気通信大学 入試問題
福田の1.5倍速演習〜合格する重要問題090〜名古屋大学2018年度理系第1問〜定積分と不等式と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 自然数nに対し、定積分$I_n$=$\displaystyle\int_0^1\frac{x^n}{x^2+1}dx$を考える。このとき、次の問いに答えよ。
(1)$I_n$+$I_{n+2}$=$\frac{1}{n+1}$を示せ。
(2)0≦$I_{n+1}$≦$I_n$≦$\frac{1}{n+1}$を示せ。
(3)$\displaystyle\lim_{n \to \infty}nI_n$ を求めよ。
(4)$S_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{2k}$ とする。このとき(1), (2)を用いて$\displaystyle\lim_{n \to \infty}S_n$ を求めよ。
2018名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 自然数nに対し、定積分$I_n$=$\displaystyle\int_0^1\frac{x^n}{x^2+1}dx$を考える。このとき、次の問いに答えよ。
(1)$I_n$+$I_{n+2}$=$\frac{1}{n+1}$を示せ。
(2)0≦$I_{n+1}$≦$I_n$≦$\frac{1}{n+1}$を示せ。
(3)$\displaystyle\lim_{n \to \infty}nI_n$ を求めよ。
(4)$S_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{2k}$ とする。このとき(1), (2)を用いて$\displaystyle\lim_{n \to \infty}S_n$ を求めよ。
2018名古屋大学理系過去問
福田の1.5倍速演習〜合格する重要問題080〜京都大学2018年度理系第5問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
この動画を見る
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題077〜東京大学2018年度理系第3問〜ベクトル方程式の表す点の存在範囲と面積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#面積、体積#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
この動画を見る
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
