数列の極限
数列の極限
福田の数学〜明治大学2022年全学部統一入試理系第１問(3)〜無限級数と極限
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(3)$k$を自然数として、
$f(x)=\sum_{n=1}^{\infty}\frac{x^{2k}}{(1+4x^{2k})^{n-1}}$
とおく。このとき、$\lim_{x \to 0}f(x)=\boxed{カ}$となる。
$\boxed{カ}$の解答群
$⓪0 ①1 ②2 ③\frac{1}{2} ④4$
$⑤\frac{1}{4} ⑥2^k ⑦\frac{1}{2^k} ⑧4^k ⑨\frac{1}{4^k}$
2022明治大学全統理系過去問
この動画を見る
(3)$k$を自然数として、
$f(x)=\sum_{n=1}^{\infty}\frac{x^{2k}}{(1+4x^{2k})^{n-1}}$
とおく。このとき、$\lim_{x \to 0}f(x)=\boxed{カ}$となる。
$\boxed{カ}$の解答群
$⓪0 ①1 ②2 ③\frac{1}{2} ④4$
$⑤\frac{1}{4} ⑥2^k ⑦\frac{1}{2^k} ⑧4^k ⑨\frac{1}{4^k}$
2022明治大学全統理系過去問
福田の数学〜早稲田大学2022年教育学部第１問(4)〜無限級数の和と部分分数分解
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{1}}$(4)次の無限級数の和は自然数となる。その自然数を求めよ。
$\sum_{n=6}^{\infty}\frac{1800}{(n-5)(n-4)(n-1)n}$
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(4)次の無限級数の和は自然数となる。その自然数を求めよ。
$\sum_{n=6}^{\infty}\frac{1800}{(n-5)(n-4)(n-1)n}$
2022早稲田大学教育学部過去問
『lim』極限について～中学生でも理解させます～
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$
\displaystyle
\lim_{x \to 0} x
$
この動画を見る
$
\displaystyle
\lim_{x \to 0} x
$
福田の数学〜早稲田大学2022年理工学部第３問〜漸化式と数列の極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{3}}\ r$を実数とする。
次の条件によって定められる数列$\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$を考える。
$a_1=r,a_{n+1}=\frac{[a_n]}{4}+\frac{a_n}{4}+\frac{5}{6}(n=1,2,3,\ldots)$
$b_1=r,b_{n+1}=\frac{b_n}{2}+\frac{7}{12}(n=1,2,3,\ldots)$
$c_1=r,c_{n+1}=\frac{c_n}{2}+\frac{5}{6}(n=1,2,3,\ldots)$
ただし、$[x]$はxを超えない最大の整数とする。以下の問いに答えよ。
(1)$\lim_{n \to \infty}b_n$と$\lim_{n \to \infty}c_n$を求めよ。
(2)$b_n \leqq a_n \leqq c_n (n=1,2,3,\ldots)$を示せ。
(3)$\lim_{n \to \infty}a_n$を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{3}}\ r$を実数とする。
次の条件によって定められる数列$\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$を考える。
$a_1=r,a_{n+1}=\frac{[a_n]}{4}+\frac{a_n}{4}+\frac{5}{6}(n=1,2,3,\ldots)$
$b_1=r,b_{n+1}=\frac{b_n}{2}+\frac{7}{12}(n=1,2,3,\ldots)$
$c_1=r,c_{n+1}=\frac{c_n}{2}+\frac{5}{6}(n=1,2,3,\ldots)$
ただし、$[x]$はxを超えない最大の整数とする。以下の問いに答えよ。
(1)$\lim_{n \to \infty}b_n$と$\lim_{n \to \infty}c_n$を求めよ。
(2)$b_n \leqq a_n \leqq c_n (n=1,2,3,\ldots)$を示せ。
(3)$\lim_{n \to \infty}a_n$を求めよ。
2022早稲田大学理工学部過去問
【誘導あり：概要欄】大学入試問題#256 神戸大学2012 #極限 #はさみうちの定理
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
（1）
$2 \leqq k$：自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
（2）
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典：2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
（1）
$2 \leqq k$：自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
（2）
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典：2012年神戸大学 入試問題
大学入試問題#218 東京都市大学(2019) 定積分と極限
単元：
#関数と極限#積分とその応用#数列の極限#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$n$：自然数
$a_n=\displaystyle \int_{1}^{\sqrt{ 2 }}x(2-x^2)^ndx$とおく
$\displaystyle \lim_{ n \to \infty }n\ a_n$を求めよ。
出典：2019年東京都市大学 入試問題
この動画を見る
$n$：自然数
$a_n=\displaystyle \int_{1}^{\sqrt{ 2 }}x(2-x^2)^ndx$とおく
$\displaystyle \lim_{ n \to \infty }n\ a_n$を求めよ。
出典：2019年東京都市大学 入試問題
【超難問】2-1が難しすぎる世界
単元：
#数列#数列とその和（等差・等比・階差・Σ）#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
深読みしすぎた2-1の計算紹介動画です
この動画を見る
深読みしすぎた2-1の計算紹介動画です
福田の数学〜九州大学2022年理系第２問〜商と余りの関係と極限
単元：
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
この動画を見る
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
福田の数学〜神戸大学2022年理系第２問〜無限等比級数の図形への応用
単元：
#大学入試過去問(数学)#複素数平面#関数と極限#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
mを3以上の自然数、$\theta=\frac{2\pi}{m}$, $C_1$を半径1の円とする。
円$C_1$に内接する(全ての頂点が$C_1$上にある)正m角形を$P_1$とし、
$P_1$に内接する($P_1$の全ての辺と接する)円を$C_2$とする。
同様に、nを自然数とするとき、円$C_n$に内接する正m角形を$P_n$とし、
$P_n$に内接する円を$C_{n+1}$とする。$C_n$の半径を$r_n,C_n$の内側
で$P_n$の外側の部分の面積を$s_n$とし、$f(m)=\sum_{n=1}^{\infty}s_n$とする。以下の問いに答えよ。
(1)$r_n,s_n$の値を$\theta,n$を用いて表せ。
(2)$f(m)$の値を$\theta$を用いて表せ。
(3)極限値$\lim_{m \to \infty}f(m)$を求めよ。
ただし必要があれば$\lim_{x \to 0}\frac{x-\sin x}{x^3}=\frac{1}{6}$を用いてよい。
2022神戸大学理系過去問
この動画を見る
mを3以上の自然数、$\theta=\frac{2\pi}{m}$, $C_1$を半径1の円とする。
円$C_1$に内接する(全ての頂点が$C_1$上にある)正m角形を$P_1$とし、
$P_1$に内接する($P_1$の全ての辺と接する)円を$C_2$とする。
同様に、nを自然数とするとき、円$C_n$に内接する正m角形を$P_n$とし、
$P_n$に内接する円を$C_{n+1}$とする。$C_n$の半径を$r_n,C_n$の内側
で$P_n$の外側の部分の面積を$s_n$とし、$f(m)=\sum_{n=1}^{\infty}s_n$とする。以下の問いに答えよ。
(1)$r_n,s_n$の値を$\theta,n$を用いて表せ。
(2)$f(m)$の値を$\theta$を用いて表せ。
(3)極限値$\lim_{m \to \infty}f(m)$を求めよ。
ただし必要があれば$\lim_{x \to 0}\frac{x-\sin x}{x^3}=\frac{1}{6}$を用いてよい。
2022神戸大学理系過去問
福田の数学〜神戸大学2022年理系第１問〜３項間の漸化式と極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
数列$\left\{a_n\right\}$を$a_1=1,a_2=2,a_{n+2}=\sqrt{a_{n+1}・a_n} (n=1,2,3,\ldots)$によって定める。
以下の問いに答えよ。
(1)全ての自然数$n$について$a_{n+1}=\frac{2}{\sqrt{a_n}}$が成り立つことを示せ。
(2)数列$\left\{b_n\right\}$を$b_n=\log a_n (n=1,2,3,\ldots)$によって定める。
$b_n$の値を$n$を用いて表せ。
(3)極限値$\lim_{n \to \infty}a_n$を求めよ。
2022神戸大学理系過去問
この動画を見る
数列$\left\{a_n\right\}$を$a_1=1,a_2=2,a_{n+2}=\sqrt{a_{n+1}・a_n} (n=1,2,3,\ldots)$によって定める。
以下の問いに答えよ。
(1)全ての自然数$n$について$a_{n+1}=\frac{2}{\sqrt{a_n}}$が成り立つことを示せ。
(2)数列$\left\{b_n\right\}$を$b_n=\log a_n (n=1,2,3,\ldots)$によって定める。
$b_n$の値を$n$を用いて表せ。
(3)極限値$\lim_{n \to \infty}a_n$を求めよ。
2022神戸大学理系過去問
福田の数学〜大阪大学2022年理系第４問〜漸化式とはさみうちの原理
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=\log(x+1)+1$とする。以下の問いに答えよ。
(1)方程式$f(x)=x$は、$x \gt 0$の範囲でただ1つの解を
もつことを示せ。
(2)(1)の解を$\alpha$とする。実数$x$が$0 \lt x \lt \alpha$を満たすならば、
次の不等式が成り立つことを示せ。
$0 \lt \frac{\alpha-f(x)}{\alpha-x} \lt f'(x)$
(3)数列$\left\{x_n\right\}$を
$x_1=1, x_{n+1}=f(x_n) (n=1,2,3,\ldots\ldots)$
で定める。このとき、全ての自然数nに対して
$\alpha -x_{n+1} \lt \frac{1}{2}(\alpha -x_n)$
が成り立つことを示せ。
(4)(3)の数列$\left\{x_n\right\}$について、$\lim_{n \to \infty}x_n=\alpha$を示せ。
2022大阪大学理系過去問
この動画を見る
$f(x)=\log(x+1)+1$とする。以下の問いに答えよ。
(1)方程式$f(x)=x$は、$x \gt 0$の範囲でただ1つの解を
もつことを示せ。
(2)(1)の解を$\alpha$とする。実数$x$が$0 \lt x \lt \alpha$を満たすならば、
次の不等式が成り立つことを示せ。
$0 \lt \frac{\alpha-f(x)}{\alpha-x} \lt f'(x)$
(3)数列$\left\{x_n\right\}$を
$x_1=1, x_{n+1}=f(x_n) (n=1,2,3,\ldots\ldots)$
で定める。このとき、全ての自然数nに対して
$\alpha -x_{n+1} \lt \frac{1}{2}(\alpha -x_n)$
が成り立つことを示せ。
(4)(3)の数列$\left\{x_n\right\}$について、$\lim_{n \to \infty}x_n=\alpha$を示せ。
2022大阪大学理系過去問
これの説明できますか？
大学入試問題#169 愛知教育大学(2013) 区分求積法
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{n+k}(log(n+k)-log\ n)$を求めよ。
出典：2013年愛知教育大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{n+k}(log(n+k)-log\ n)$を求めよ。
出典：2013年愛知教育大学 入試問題
円は何角形ですか？
単元：
#関数と極限#数列の極限#平面図形その他#数学(高校生)#数Ⅲ
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
円は何角形でしょう？何角形から円となるでしょう？
この動画を見る
円は何角形でしょう？何角形から円となるでしょう？
大学入試問題#152 東京工業大学(2002) 極限
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{log\ n}(1+\displaystyle \frac{1}{2}+・・・+\displaystyle \frac{1}{n})$を求めよ。
出典：2002年東京工業大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{log\ n}(1+\displaystyle \frac{1}{2}+・・・+\displaystyle \frac{1}{n})$を求めよ。
出典：2002年東京工業大学 入試問題
福田の数学・入試問題解説〜東北大学2022年理系第３問〜無限級数の和とはさみうちの原理
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
正の整数nに対して、
$S_n=\sum_{k=1}^n(\sqrt{1+\frac{k}{n^2}}-1)$
とする。
(1)正の実数xに対して、次の不等式が成り立つことを示せ。
$\frac{x}{2+x} \leqq \sqrt{1+x}-1 \leqq \frac{x}{2}$
(2)極限値$\lim_{n \to \infty}S_n$を求めよ。
2022東北大学理系過去問
この動画を見る
正の整数nに対して、
$S_n=\sum_{k=1}^n(\sqrt{1+\frac{k}{n^2}}-1)$
とする。
(1)正の実数xに対して、次の不等式が成り立つことを示せ。
$\frac{x}{2+x} \leqq \sqrt{1+x}-1 \leqq \frac{x}{2}$
(2)極限値$\lim_{n \to \infty}S_n$を求めよ。
2022東北大学理系過去問
いくつでしょうか？
単元：
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 2^{\frac{1}{4}}・ 4^{\frac{1}{8}}・8^{\frac{1}{16}}・16^{\frac{1}{32}}……\infty $
これを解け.
この動画を見る
$ 2^{\frac{1}{4}}・ 4^{\frac{1}{8}}・8^{\frac{1}{16}}・16^{\frac{1}{32}}……\infty $
これを解け.
大学入試問題#118 防衛医科大学(2012) 区分求積法
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典：2012年防衛医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典：2012年防衛医科大学 入試問題
極限ってこういうこと？
大学入試問題#109 大阪府立大学(2010) 無限級数
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1$
$a_{n+1}=\displaystyle \frac{n}{n+5}\ a_n$のとき
$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典：2010年大阪府立大学 入試問題
この動画を見る
$a_1=1$
$a_{n+1}=\displaystyle \frac{n}{n+5}\ a_n$のとき
$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典：2010年大阪府立大学 入試問題
大学入試問題#102 高知女子大学(1988) 無限級数
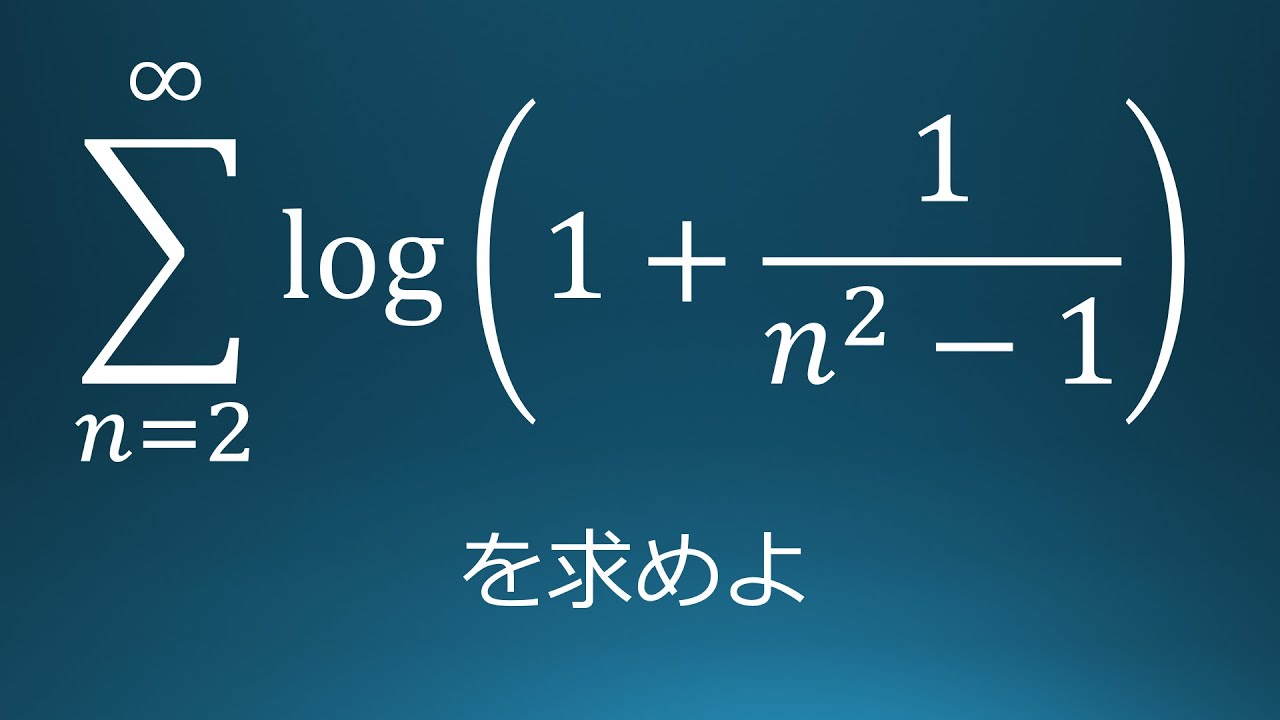
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典：1988年高知女子大学 入試問題
この動画を見る
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典：1988年高知女子大学 入試問題
大学入試問題#86 防衛医科大学(1988) 極限
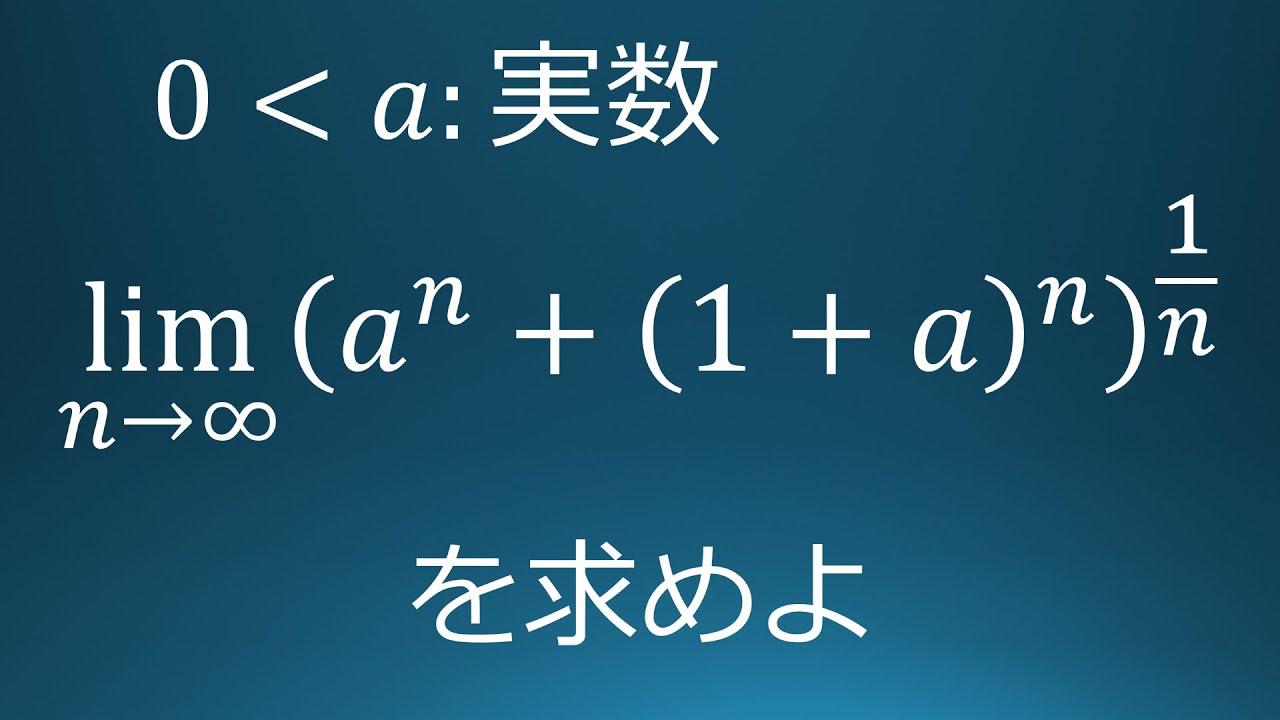
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典：1988年防衛医科大学 入試問題
この動画を見る
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典：1988年防衛医科大学 入試問題
大学入試問題#77 京都大学(2002) 数列と極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典：2002年京都大学 入試問題
この動画を見る
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典：2002年京都大学 入試問題
【概要欄に正確な文章と説明の補足】大学入試問題#76 京都大学(2007) 数列と極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$x,y$：異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典：2007年京都大学 入試問題
この動画を見る
$x,y$：異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典：2007年京都大学 入試問題
大学入試問題#74 神戸大学(1991) 数列と極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：1991年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：1991年神戸大学 入試問題
大学入試問題#73 京都大学(2012) 極限
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(1+a^n)^{\frac{1}{n}}$の極限を求めよ。
出典：2012年京都大学 入試問題
この動画を見る
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(1+a^n)^{\frac{1}{n}}$の極限を求めよ。
出典：2012年京都大学 入試問題
【数Ⅲ】極限：極限の定形不定形をマスターしよう！
単元：
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
極限の考え方の基本です。変形が必要な場合と必要でない場合の違いをチェックしましょう！
この動画を見る
極限の考え方の基本です。変形が必要な場合と必要でない場合の違いをチェックしましょう！
#42 数検1級1次 過去問 極限値
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{n+1}{\sqrt[ n ]{ n! }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{n+1}{\sqrt[ n ]{ n! }}$の極限値を求めよ。
【数Ⅲ】極限：数列の極限と関数の極限の違いを解説します
大学入試問題#40 東京理科大学(2021) 数列と極限
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：2021年東京理科大学 入試問題
この動画を見る
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：2021年東京理科大学 入試問題