 微分とその応用
微分とその応用
 微分とその応用
微分とその応用
福田の数学〜筑波大学2023年理系第5問〜関数の増減と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $f(x)$=$x^{-2}e^x$ ($x$>0)とし、曲線$y$=$f(x)$をCとする。また$h$を正の実数とする。さらに、正の実数$t$に対して、曲線C、2直線$x$=$t$, $x$=$t$+$h$、および$x$軸で囲まれた図形の面積を$g(t)$とする。
(1)$g'(t)$を求めよ。
(2)$g(t)$を最小にする$t$がただ1つ存在することを示し、その$t$を$h$を用いて表せ。
(3)(2)で得られた$t$を$t(h)$とする。このとき極限値$\displaystyle\lim_{h \to +0}t(h)$を求めよ。
この動画を見る
$\Large\boxed{5}$ $f(x)$=$x^{-2}e^x$ ($x$>0)とし、曲線$y$=$f(x)$をCとする。また$h$を正の実数とする。さらに、正の実数$t$に対して、曲線C、2直線$x$=$t$, $x$=$t$+$h$、および$x$軸で囲まれた図形の面積を$g(t)$とする。
(1)$g'(t)$を求めよ。
(2)$g(t)$を最小にする$t$がただ1つ存在することを示し、その$t$を$h$を用いて表せ。
(3)(2)で得られた$t$を$t(h)$とする。このとき極限値$\displaystyle\lim_{h \to +0}t(h)$を求めよ。
福田の数学〜神戸大学2023年理系第5問〜媒介変数表示で表された曲線と面積

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 媒介変数表示
$x$=$\sin t$, $y$=$\cos(t-\frac{\pi}{6})\sin t$ (0≦$t$≦$\pi$)
で表される曲線をCとする。以下の問いに答えよ。
(1)$\frac{dx}{dt}$=0 または $\frac{dy}{dt}$=0 となる$t$の値を求めよ。
(2)Cの概形を$xy$平面上に描け。
(3)Cの$y$≦0 の部分と$x$軸で囲まれた図形の面積を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{5}$ 媒介変数表示
$x$=$\sin t$, $y$=$\cos(t-\frac{\pi}{6})\sin t$ (0≦$t$≦$\pi$)
で表される曲線をCとする。以下の問いに答えよ。
(1)$\frac{dx}{dt}$=0 または $\frac{dy}{dt}$=0 となる$t$の値を求めよ。
(2)Cの概形を$xy$平面上に描け。
(3)Cの$y$≦0 の部分と$x$軸で囲まれた図形の面積を求めよ。
2023神戸大学理系過去問
大学入試問題#571「綺麗な基本問題」 By 僚太さん #微分方程式

単元:
#微分とその応用#その他#速度と近似式#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$x \neq 0$
$3x^2f(x)-3\displaystyle \int_{1}^{x} t\ f(t)dt=1$を満たす関数$f(x)$を求めよ
この動画を見る
$x \neq 0$
$3x^2f(x)-3\displaystyle \int_{1}^{x} t\ f(t)dt=1$を満たす関数$f(x)$を求めよ
大学入試問題#570「ほんまにええ問題や~~」 By にっし~Diaryさん #解の個数

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x$の方程式
$(x^2-6x+8)^2-k(x^2-6x+8)+4=0$の実数解の個数を調べよ。
この動画を見る
$x$の方程式
$(x^2-6x+8)^2-k(x^2-6x+8)+4=0$の実数解の個数を調べよ。
福田の数学〜九州大学2023年理系第4問〜加法定理が成り立つ関数を調べるPART2

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第4問〜加法定理が成り立つ関数を調べるPART1

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
福田の数学〜名古屋大学2023年文系第1問〜3次関数と2次関数のグラフ

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ aを実数とし、2つの関数$f(x)=x^3-(a+2)x^2+2a+1 $と$g(x)$=$-x^2+1$ を考える。
(1)$f(x)$-$g(x)$ を因数分解せよ。
(2)y=$f(x)$とy=$g(x)$のグラフの共有点が2個であるようなaを求めよ。
(3)aは(2)の条件を満たし、さらに$f(x)$の極大値は1よりも大きいとする。
y=$f(x)$とy=$g(x)$のグラフを同じ座標平面に図示せよ。
2023名古屋大学文系過去問
この動画を見る
$\Large\boxed{1}$ aを実数とし、2つの関数$f(x)=x^3-(a+2)x^2+2a+1 $と$g(x)$=$-x^2+1$ を考える。
(1)$f(x)$-$g(x)$ を因数分解せよ。
(2)y=$f(x)$とy=$g(x)$のグラフの共有点が2個であるようなaを求めよ。
(3)aは(2)の条件を満たし、さらに$f(x)$の極大値は1よりも大きいとする。
y=$f(x)$とy=$g(x)$のグラフを同じ座標平面に図示せよ。
2023名古屋大学文系過去問
福田の数学〜名古屋大学2023年理系第3問〜方程式の負の実数解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ (1)方程式$e^x$=$\frac{2x^3}{x-1}$ の負の実数解の個数を求めよ。
(2)$y$=$x(x^2-3)$と$y$=$e^x$のグラフの$x$<0における共有点の個数を求めよ。
(3)$a$を正の実数とし、関数$f(x)$=$x(x^2-a)$を考える。$y$=$f(x)$と$y$=$e^x$のグラフの$x$<0における共有点は1個のみであるとする。このような$a$がただ1つ存在することを示せ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{3}$ (1)方程式$e^x$=$\frac{2x^3}{x-1}$ の負の実数解の個数を求めよ。
(2)$y$=$x(x^2-3)$と$y$=$e^x$のグラフの$x$<0における共有点の個数を求めよ。
(3)$a$を正の実数とし、関数$f(x)$=$x(x^2-a)$を考える。$y$=$f(x)$と$y$=$e^x$のグラフの$x$<0における共有点は1個のみであるとする。このような$a$がただ1つ存在することを示せ。
2023名古屋大学理系過去問
福田の数学〜名古屋大学2023年理系第2問〜回転体の体積と関数の増減と最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#面積、体積#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
【数Ⅲ】微分法:整式の次数に着目して解く問題

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)$は0でない整式で次を満たすとする。
・$xf''(x) + (1 - x)f'(x) + 3f(x) = 0$
・$f(0) = 1$
(1)$f(x)$の次数を求めよ
(2)$f(x)$を求めよ
この動画を見る
$f(x)$は0でない整式で次を満たすとする。
・$xf''(x) + (1 - x)f'(x) + 3f(x) = 0$
・$f(0) = 1$
(1)$f(x)$の次数を求めよ
(2)$f(x)$を求めよ
大学院入試問題#1「間違えてたらすみません」 岡山大学大学院 #微分方程式

単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
この動画を見る
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
福田の数学〜東北大学2023年文系第3問〜軸の動く最大最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年理系第6問〜線分の通過範囲の面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第2問〜三角方程式の解の個数とその極限

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
福田の数学〜慶應義塾大学2023年看護医療学部第4問〜絶対値の付いた関数と領域における最大最小
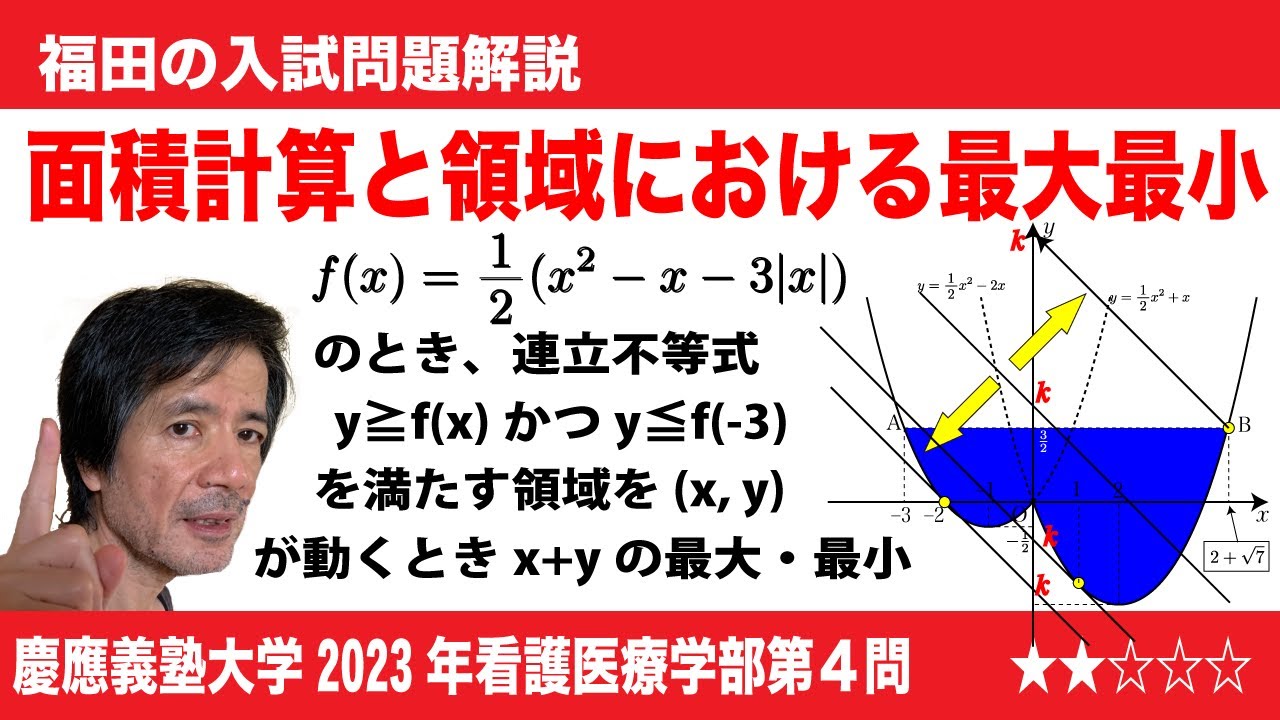
単元:
#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)をf(x)=$\frac{1}{2}$($x^2$-$x$-3|$x$|)で定める。以下に答えなさい。
(1)y=f(x)のグラフをかきなさい。
(2)曲線y=f(x)上の点A(-3, f(-3))を通り、点Aにおける接線に垂直な直線lの方程式はy=$\boxed{\ \ ニ\ \ }$である。また、曲線と直線lは2つの共有点をもつが点Aとは異なる共有点の座標は$\boxed{\ \ ヌ\ \ }$である。さらに、曲線y=f(x)と直線lで囲まれた図形の面積は$\boxed{\ \ ネ\ \ }$である。
(3)連立不等式y≧f(x), y≦f(-3)の表す領域をDとする。点(x,y)がこの領域Dを動くとき、x+yは(x,y)=$\boxed{\ \ ノ\ \ }$のとき最大値$\boxed{\ \ ハ\ \ }$をとり、
(x,y)=$\boxed{\ \ ヒ\ \ }$のうち最小値$\boxed{\ \ フ\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
神戸大 3次関数の最大最小

単元:
#大学入試過去問(数学)#式と証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
この動画を見る
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART2〜円に内接する円の性質
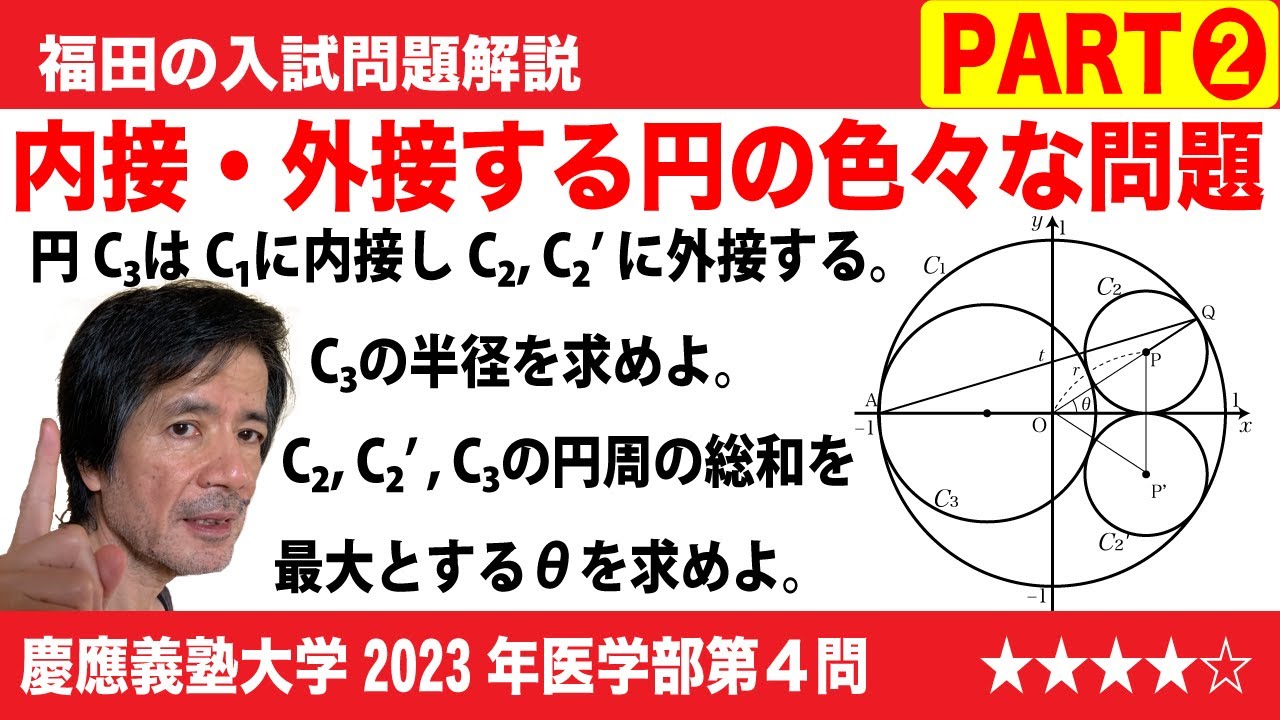
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
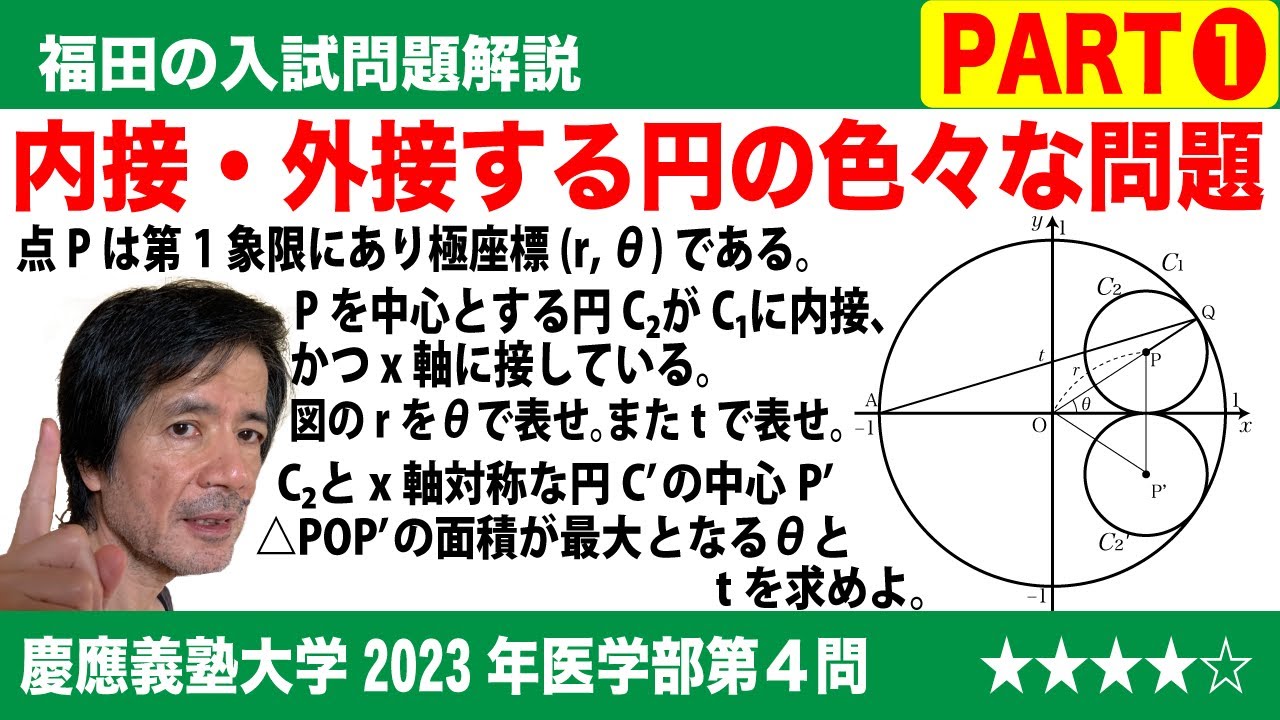
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年医学部第1問(3)〜曲線と直線で囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)曲線y=$x$$\log(x^2+1)$のx≧0の部分をCとすると、点(1, log2)におけるCの接線lの方程式はy=$\boxed{\ \ く\ \ }$である。
また、曲線Cと直線l、およびy軸で囲まれた図形の面積は$\boxed{\ \ け\ \ }$である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (3)曲線y=$x$$\log(x^2+1)$のx≧0の部分をCとすると、点(1, log2)におけるCの接線lの方程式はy=$\boxed{\ \ く\ \ }$である。
また、曲線Cと直線l、およびy軸で囲まれた図形の面積は$\boxed{\ \ け\ \ }$である。
2023慶應義塾大学医学部過去問
福田の数学〜早稲田大学2023年理工学部第4問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#微分とその応用#複素数平面#図形への応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
この動画を見る
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
福田の数学〜早稲田大学2023年理工学部第3問〜逆関数とで囲まれる面積

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 実数xに対して関数f(x)をf(x)=$e^{x-2}$で定め、正の実数xに対して関数g(x)をg(x)=$\log x$+2で定める。またy=f(x), y=g(x)のグラフをそれぞれ$C_1$,$C_2$とする。以下の問いに答えよ。
(1)f(x)とg(x)がそれぞれ互いの逆関数であることを示せ。
(2)直線y=xと$C_1$が2点で交わることを示せ。ただし、必要なら2<e<3を証明しないで用いてよい。
(3)直線y=xと$C_1$との2つの交点のx座標を$\alpha$, $\beta$とする。ただし$\alpha$<$\beta$とする。
直線y=xと$C_1$,$C_2$をすべて同じxy平面上に図示せよ。
(4)$C_1$と$C_2$で囲まれる図形の面積を(3)の$\alpha$と$\beta$の多項式で表せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{3}$ 実数xに対して関数f(x)をf(x)=$e^{x-2}$で定め、正の実数xに対して関数g(x)をg(x)=$\log x$+2で定める。またy=f(x), y=g(x)のグラフをそれぞれ$C_1$,$C_2$とする。以下の問いに答えよ。
(1)f(x)とg(x)がそれぞれ互いの逆関数であることを示せ。
(2)直線y=xと$C_1$が2点で交わることを示せ。ただし、必要なら2<e<3を証明しないで用いてよい。
(3)直線y=xと$C_1$との2つの交点のx座標を$\alpha$, $\beta$とする。ただし$\alpha$<$\beta$とする。
直線y=xと$C_1$,$C_2$をすべて同じxy平面上に図示せよ。
(4)$C_1$と$C_2$で囲まれる図形の面積を(3)の$\alpha$と$\beta$の多項式で表せ。
2023早稲田大学理工学部過去問
【数Ⅲ】東大の文系の問題を微分で解いてみた【東京大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
kを正の実数とし,二次方程式$x^{2}+x-k=0$の二つの実数解を、$\alpha,\beta$とする。
$kがk>2$の範囲を動くとき,
$\displaystyle \frac{\alpha^{3}}{1-\beta}+\displaystyle \frac{\beta^{3}}{1-\alpha}$の最小値を求めよ。
東大過去問
この動画を見る
kを正の実数とし,二次方程式$x^{2}+x-k=0$の二つの実数解を、$\alpha,\beta$とする。
$kがk>2$の範囲を動くとき,
$\displaystyle \frac{\alpha^{3}}{1-\beta}+\displaystyle \frac{\beta^{3}}{1-\alpha}$の最小値を求めよ。
東大過去問
【数Ⅲ】微分の応用:漸近線があるグラフの概形part2

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=\dfrac{x^3}{x^2-4}$ の漸近線を求めよ
この動画を見る
$f(x)=\dfrac{x^3}{x^2-4}$ の漸近線を求めよ
大学入試問題#503「微分してもよさげだけど・・・」 #藤田医科大学 (2023) #判別式

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{8x^2+5}{x^2-3x+6}$
の最大値を$M$、最小値を$m$とするとき$\displaystyle \frac{M}{m}$を求めよ
出典:2023年藤田医科大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{8x^2+5}{x^2-3x+6}$
の最大値を$M$、最小値を$m$とするとき$\displaystyle \frac{M}{m}$を求めよ
出典:2023年藤田医科大学 入試問題
【数Ⅲ】微分の応用:漸近線があるグラフの概形part1

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)= 2x+\sqrt{x^2-1}$ の漸近線を求めよ
この動画を見る
$f(x)= 2x+\sqrt{x^2-1}$ の漸近線を求めよ
福田の数学〜北海道大学2023年理系第5問〜中間値の定理と関数の増減PART2

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ a,bを$a^2$+$b^2$< 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$< 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第3問〜指数方程式の解

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 以下の問いに答えよ。ただし、eは自然対数の底を表す。
(1)kを実数の定数とし、f(x)=$xe^{-x}$とおく。方程式f(x)=kの異なる実数解の個数を求めよ。ただし、$\displaystyle\lim_{x \to \infty}f(x)$=0を用いてもよい。
(2)$xye^{-(x+y)}$=cを満たす正の実数x, yの組がただ1つ存在するときの実数cの値を求めよ。
(3)$xye^{-(x+y)}$=$\frac{3}{e^4}$を満たす正の実数x, yを考えるとき、yのとりうる値の最大値とそのときのxの値を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。ただし、eは自然対数の底を表す。
(1)kを実数の定数とし、f(x)=$xe^{-x}$とおく。方程式f(x)=kの異なる実数解の個数を求めよ。ただし、$\displaystyle\lim_{x \to \infty}f(x)$=0を用いてもよい。
(2)$xye^{-(x+y)}$=cを満たす正の実数x, yの組がただ1つ存在するときの実数cの値を求めよ。
(3)$xye^{-(x+y)}$=$\frac{3}{e^4}$を満たす正の実数x, yを考えるとき、yのとりうる値の最大値とそのときのxの値を求めよ。
2023北海道大学理系過去問
福田の数学〜大阪大学2023年文系第2問〜対数関数と3次関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 正の実数a, xに対して
y=$(\log_{\frac{1}{2}}x)^3$+$a\log_{\sqrt 2}x$$(\log_4x^3)$
とする。
(1)t=$\log_2x$とするとき、yをa, tを用いて表せ。
(2)xが$\frac{1}{2}$≦x≦8の範囲を動くとき、yの最大値Mをaを用いて表せ。
2023大阪大学文系過去問
この動画を見る
$\Large\boxed{2}$ 正の実数a, xに対して
y=$(\log_{\frac{1}{2}}x)^3$+$a\log_{\sqrt 2}x$$(\log_4x^3)$
とする。
(1)t=$\log_2x$とするとき、yをa, tを用いて表せ。
(2)xが$\frac{1}{2}$≦x≦8の範囲を動くとき、yの最大値Mをaを用いて表せ。
2023大阪大学文系過去問
福田の数学〜大阪大学2023年理系第3問〜三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Pを座標平面上の点とし、点Pの座標を(a,b)とする。-π≦t≦πの範囲にある実数tのうち、曲線y=$\cos x$上の点(t, $\cos t$)における接線が点Pを通るという条件をみたすものの個数をN(P)とする。N(P)=4かつ0<a<πをみたすような点Pの存在範囲を座標平面上に図示せよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{3}$ Pを座標平面上の点とし、点Pの座標を(a,b)とする。-π≦t≦πの範囲にある実数tのうち、曲線y=$\cos x$上の点(t, $\cos t$)における接線が点Pを通るという条件をみたすものの個数をN(P)とする。N(P)=4かつ0<a<πをみたすような点Pの存在範囲を座標平面上に図示せよ。
2023大阪大学理系過去問
