 不定積分
不定積分
 不定積分
不定積分
大学入試問題#368「よくみる積分」 防衛医科大学校2014 #不定積分
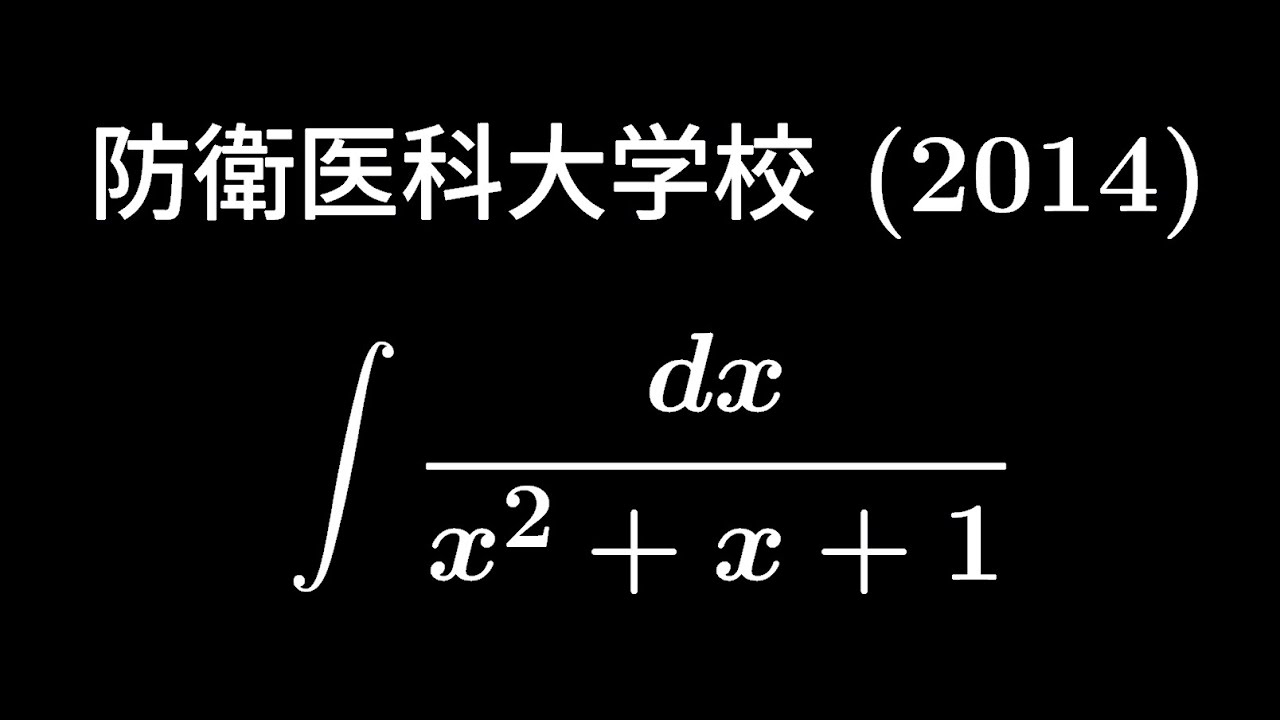
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典:2014年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典:2014年防衛医科大学 入試問題
大学入試問題#364「計算が大変でした」 岩手大学2014 #不定積分
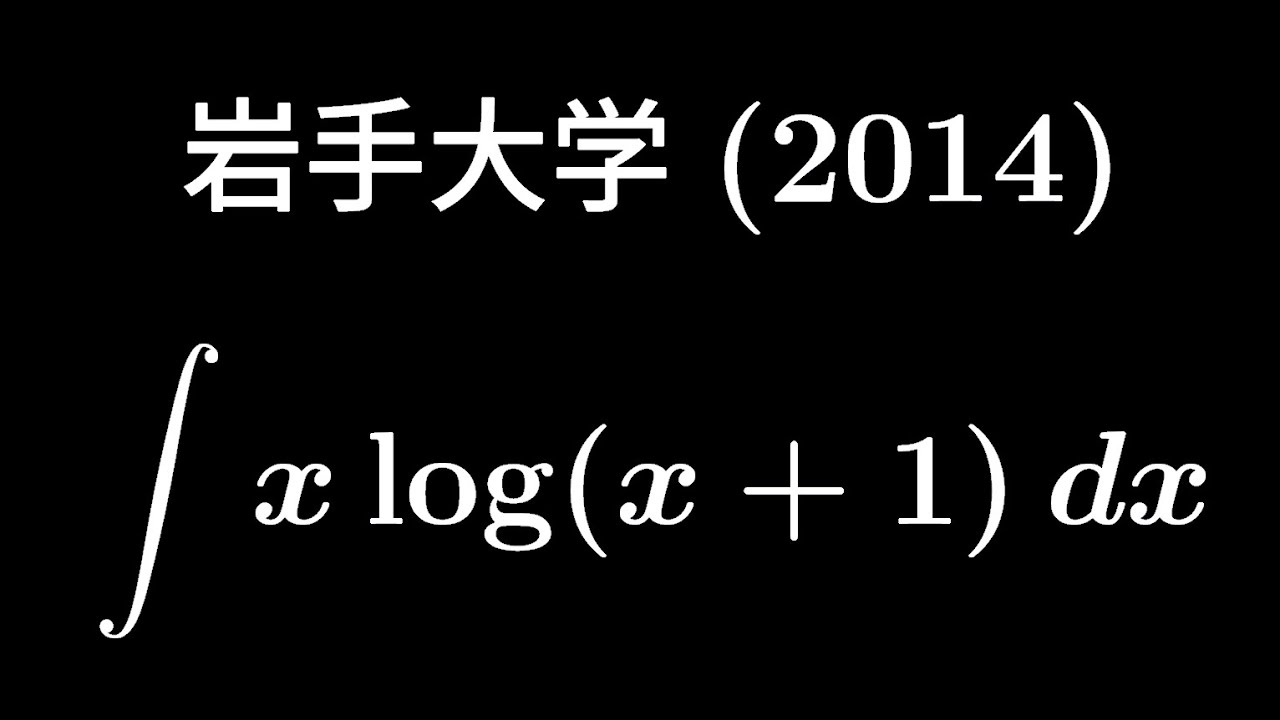
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\ log(x+1)dx$
出典:2014年岩手大学 入試問題
この動画を見る
$\displaystyle \int x\ log(x+1)dx$
出典:2014年岩手大学 入試問題
大学入試問題#352「よく出題されそうな綺麗な問題」 京都工芸繊維大学(2011) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2 dx$
出典:2011年京都工芸繊維大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2 dx$
出典:2011年京都工芸繊維大学 入試問題
大学入試問題#341「部分積分の心を・・・」 立教大学 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
この動画を見る
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
【最後の足し算で計算ミスしてます。】大学入試問題#334 広島市立大学(2011) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2+1}{x+1}dx$
出典:2011年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2+1}{x+1}dx$
出典:2011年広島市立大学 入試問題
大学入試問題#332 Instagram #不定積分
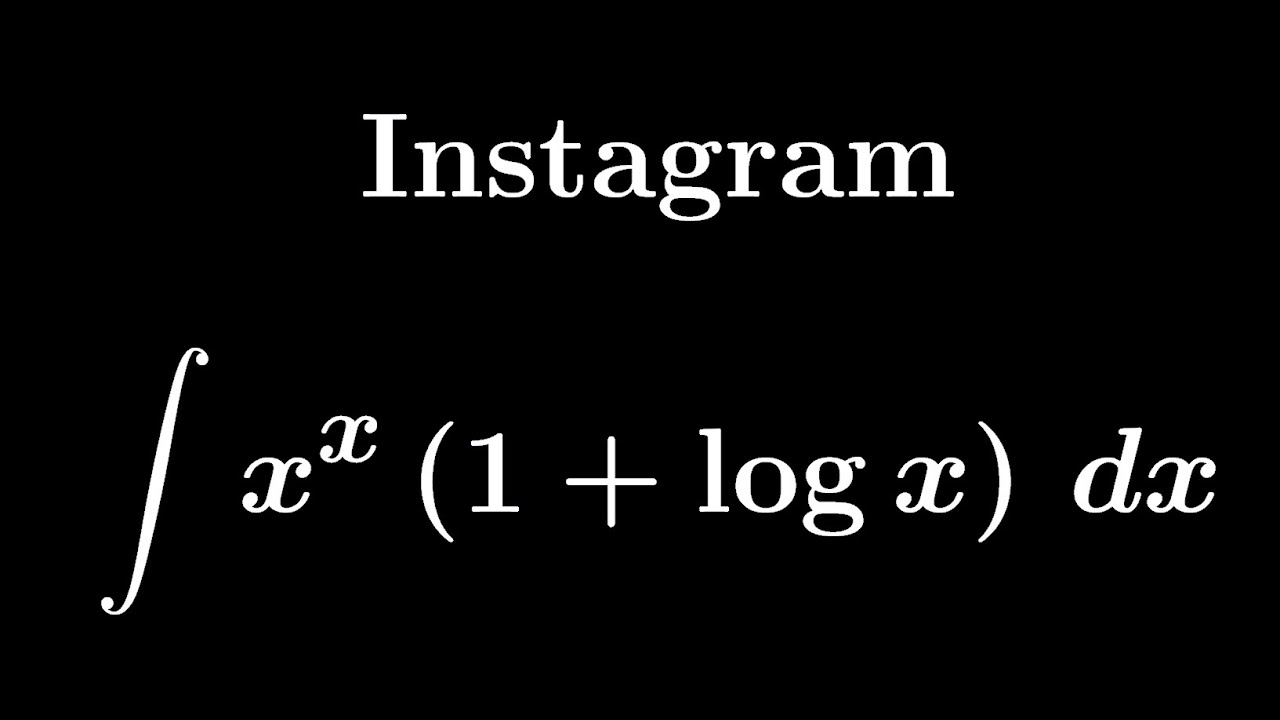
【概要欄必読】大学入試問題#326 Instagram #不定積分
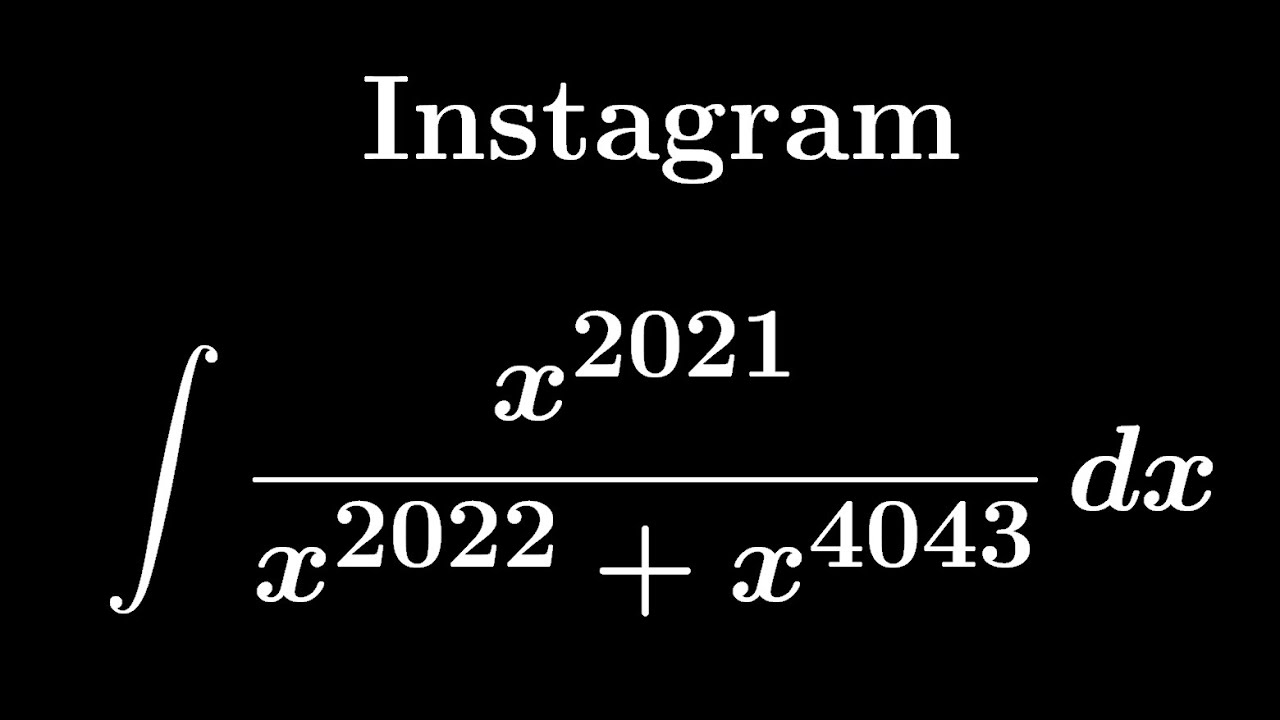
単元:
#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^{2021}}{x^{2022}+x^{4043}}dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x^{2021}}{x^{2022}+x^{4043}}dx$
大学入試問題#319 電気通信大学(2010) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
大学入試問題#236 茨城大学(2012) 改 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典:2012年茨城大学 入試問題
大学入試問題#231 電気通信大学(2012) #不定積分

単元:
#大学入試過去問(数学)#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:2012年電気通信大学 入試問題
この動画を見る
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:2012年電気通信大学 入試問題
大学入試問題#226 信州大学(2012) #不定積分
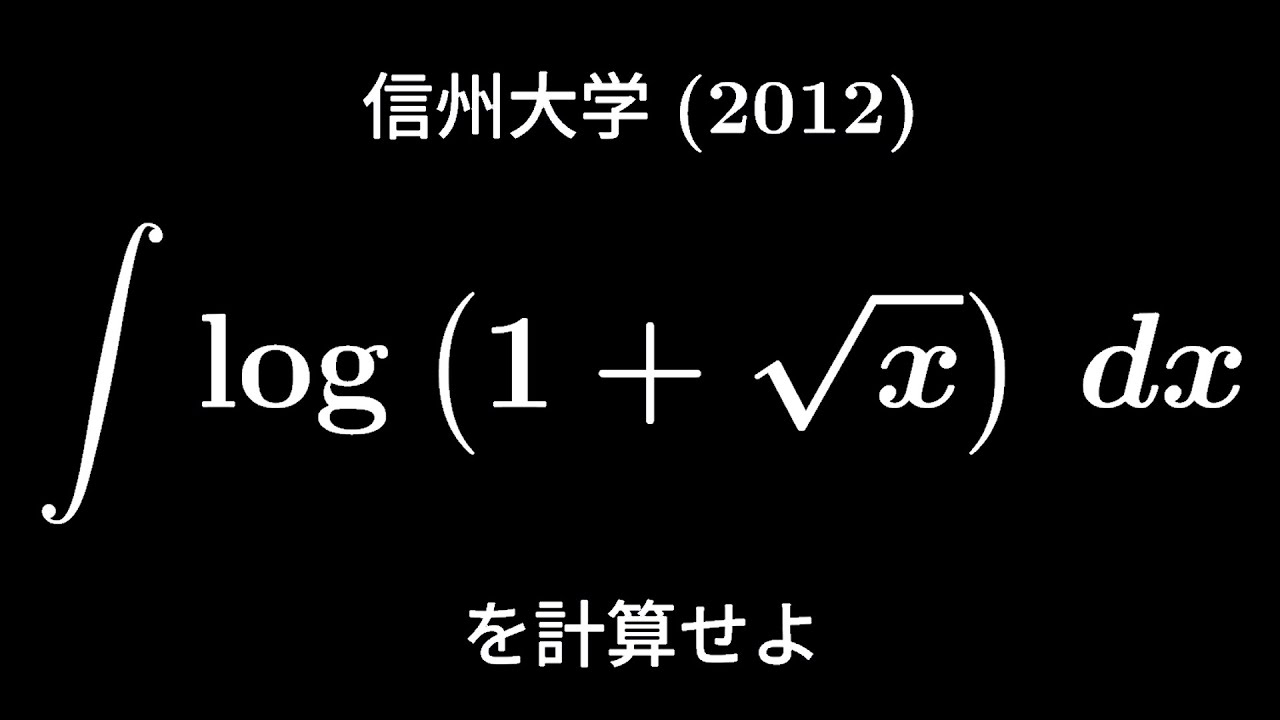
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+\sqrt{ x })dx$を計算せよ
出典:2012年信州大学 入試問題
この動画を見る
$\displaystyle \int log(1+\sqrt{ x })dx$を計算せよ
出典:2012年信州大学 入試問題
大学入試問題#224 防衛医科大学(2015) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$を計算せよ
出典:2015年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$を計算せよ
出典:2015年防衛医科大学 入試問題
大学入試問題#222 広島市立大学2015 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$を計算せよ
出典:2015年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$を計算せよ
出典:2015年広島市立大学 入試問題
大学入試問題#210 宮崎大学(2018) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^3}{x^2-4}\ dx$を計算せよ。
出典:2018年宮崎大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3}{x^2-4}\ dx$を計算せよ。
出典:2018年宮崎大学 入試問題
大学入試問題#207 埼玉大学(2006) 不定積分
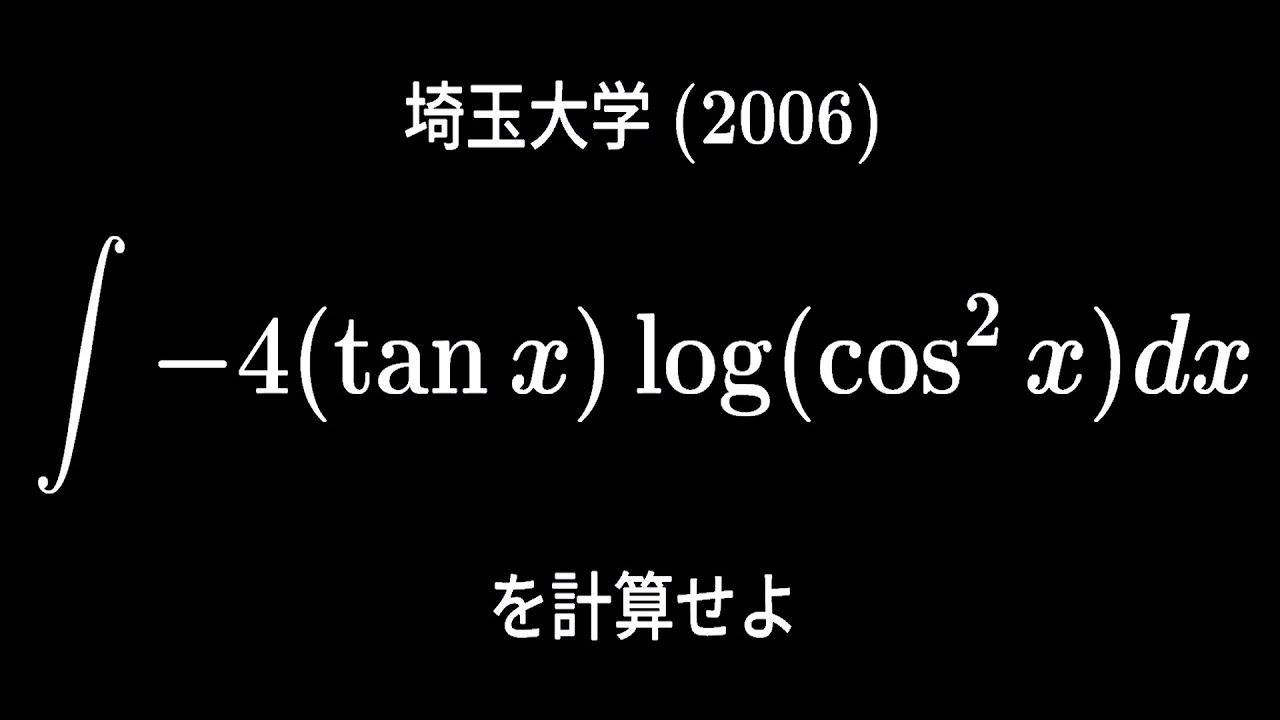
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int -4\tan\ x\ log(\cos^2x)dx$を計算せよ。
出典:2006年埼玉大学 入試問題
この動画を見る
$\displaystyle \int -4\tan\ x\ log(\cos^2x)dx$を計算せよ。
出典:2006年埼玉大学 入試問題
大学入試問題#206 東京農工大学(2020) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京農工大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{e^x+2}\ dx$
出典:2020年東京農業工業大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x+2}\ dx$
出典:2020年東京農業工業大学 入試問題
大学入試問題#194 横浜国立大学 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sqrt{ 1-e^{-2x} }\ dx$を計算せよ。
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ 1-e^{-2x} }\ dx$を計算せよ。
出典:横浜国立大学 入試問題
大学入試問題#192 東京大学(昭和9年) 不定積分 3手1組の好手順

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ 1+x^6 }}\ dx$を計算せよ。
出典:昭和9年東京大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ 1+x^6 }}\ dx$を計算せよ。
出典:昭和9年東京大学 入試問題
大学入試問題#186 京都大学医学部(大正15年) 不定積分 たぶん難問

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{(x+1)\sqrt{ x^2-1 }}$を計算せよ。
出典:大正15年京都大学医学部 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{(x+1)\sqrt{ x^2-1 }}$を計算せよ。
出典:大正15年京都大学医学部 入試問題
大学入試問題#182 横浜国立大学 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2dx$を計算せよ
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2dx$を計算せよ
出典:横浜国立大学 入試問題
大学入試問題#176 日本医科大学(2019) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sqrt{ x^2+1 }\ dx$
出典:2019年日本医科大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ x^2+1 }\ dx$
出典:2019年日本医科大学 入試問題
大学入試問題#173 和歌山県立医科大学(2000) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#和歌山県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \cos^2x\ \sin^3x\ dx$を計算せよ。
出典:2000年和歌山県立医科大学 入試問題
この動画を見る
$\displaystyle \int \cos^2x\ \sin^3x\ dx$を計算せよ。
出典:2000年和歌山県立医科大学 入試問題
大学入試問題#170 東北大学(大正14年) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(log\ x)+\displaystyle \frac{1}{log\ x}\ dx$
出典:大正14年東北大学 入試問題
この動画を見る
$\displaystyle \int log(log\ x)+\displaystyle \frac{1}{log\ x}\ dx$
出典:大正14年東北大学 入試問題
大学入試問題#166 東京大学 改 (2022) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\cos\ x\ log(\cos\ x)dx$を求めよ。
出典:2022年東京大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\cos\ x\ log(\cos\ x)dx$を求めよ。
出典:2022年東京大学 入試問題
大学入試問題#142 広島市立大学(2014) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \cos\sqrt{ x }\ dx$を計算せよ。
出典:2014年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \cos\sqrt{ x }\ dx$を計算せよ。
出典:2014年広島市立大学 入試問題
大学入試問題#134 京都工芸繊維大学(2018) 不定積分

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \{log(3+\cos^2\theta)\}\cos\theta d \theta$を計算せよ。
出典:2018年京都工芸繊維大学 入試問題
この動画を見る
$\displaystyle \int \{log(3+\cos^2\theta)\}\cos\theta d \theta$を計算せよ。
出典:2018年京都工芸繊維大学 入試問題
【数Ⅲ】微分法・積分法:<公式忘れても大丈夫!>三角関数の微積分 ~ぐるぐる回そう~

単元:
#微分とその応用#積分とその応用#色々な関数の導関数#不定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
この動画を見る
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
大学入試問題#126 慶應大学医学部(2005) 不定積分
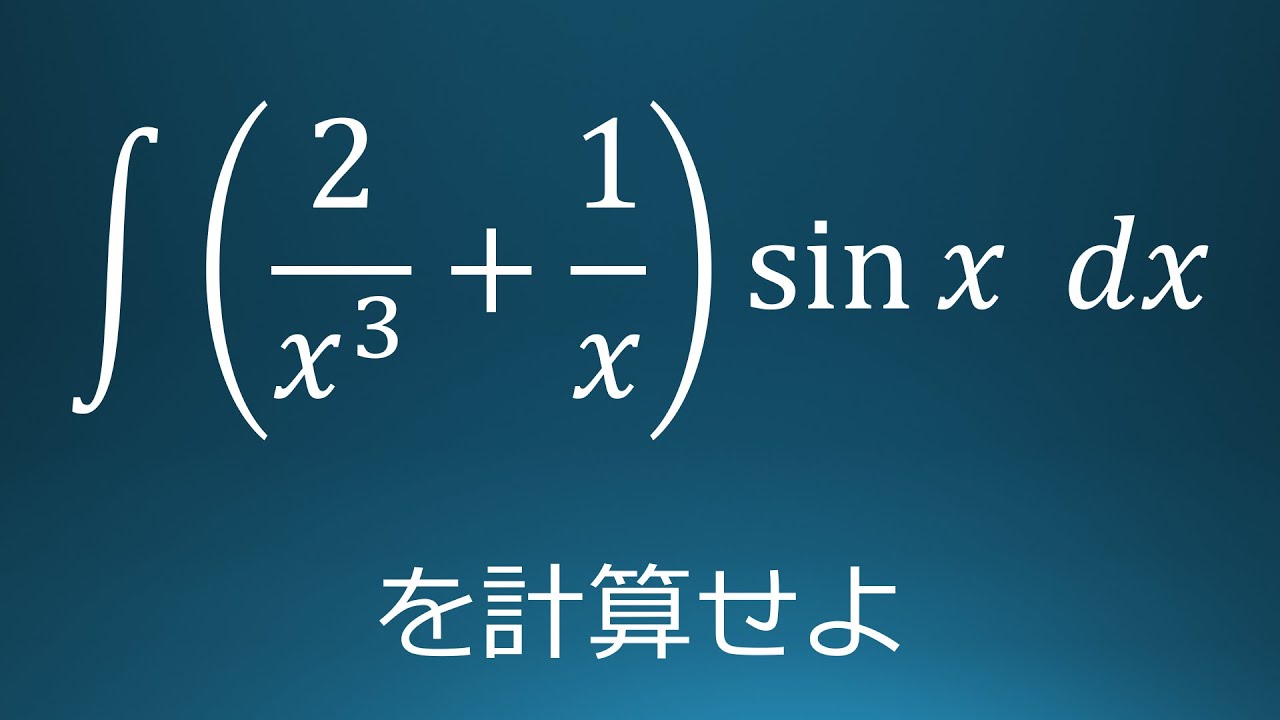
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{2}{x^3}+\displaystyle \frac{1}{x})\sin\ x\ dx$を計算せよ。
出典:2005年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{2}{x^3}+\displaystyle \frac{1}{x})\sin\ x\ dx$を計算せよ。
出典:2005年慶應義塾大学 入試問題
大学入試問題#124 高知大学(2020) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
大学入試問題#112 琉球大学(1989) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$-1 \neq \alpha$:定数
$\displaystyle \int \displaystyle \frac{(log\ x)^\alpha}{x}\ log(\log\ x)dx$を計算せよ。
出典:1989年琉球大学 入試問題
この動画を見る
$-1 \neq \alpha$:定数
$\displaystyle \int \displaystyle \frac{(log\ x)^\alpha}{x}\ log(\log\ x)dx$を計算せよ。
出典:1989年琉球大学 入試問題
